Борисенко О.А. Дискретна математика

Подождите немного. Документ загружается.

Перший крок наведеного алгоритму являє собою звичайну

(неповну) індукцію, яка реалізує індукційний підхід до науки в

цілому.

Другий і третій кроки алгоритму є наслідком дії принципу

математичної індукції та реалізують його практично. Принцип

математичної індукції гарантує за умови, якщо другий і третій кроки

методу виконані, що твердження Р(п) дійсне. Гіри цьому другий крок

грунтується на лемі 1 і є основою (базою) метода математичної

індукції, а третій - на лемі 2, яка визначає індукційний крок (перехід)

методу.

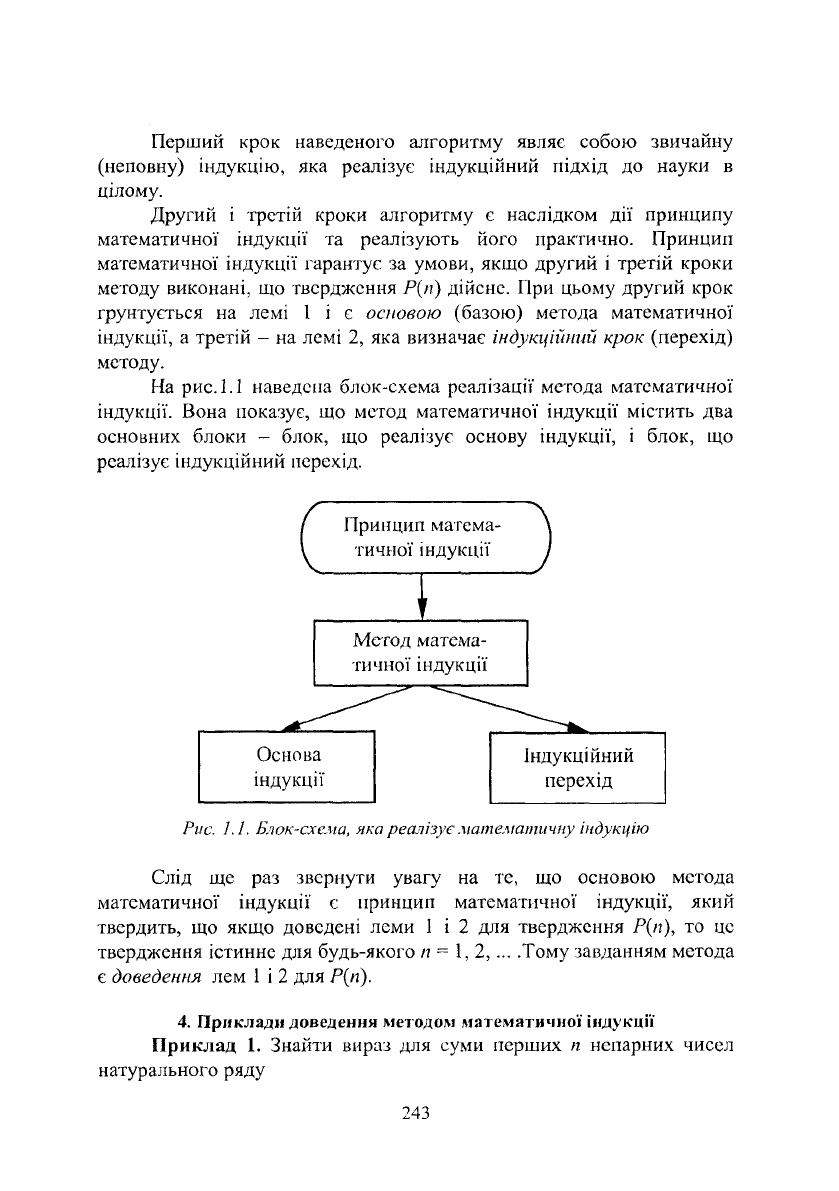
На рис.

1.1

наведена блок-схема реалізації метода математичної

індукції. Вона показує, що метод математичної індукції містить два

основних блоки - блок, що реалізує основу індукції, і блок, що

реалізує індукційний перехід.

Рис. 1.1. Блок-схема, яка реалізує математичну індукцію

Слід ще раз звернути увагу на те, що основою метода

математичної індукції є принцип математичної індукції, який

твердить, що якщо доведені леми 1 і 2 для твердження Р(п'), то це

твердження істинне для будь-якого

= 1,2,... .Тому завданням метода

є доведення лем 1 і 2 для Р(п).

4. Приклади доведення методом математичної індукції

Приклад 1. Знайти вираз для суми перших п непарних чисел

натурального ряду

243

Р(л) =

+ 3 + ... + (2л - 1).

Розв'язання. На основі аналізу перших початкових чисел

натурального ряду за допомогою неповної індукції отримуємо

гіпотезу, що Р(п) -п

Застосувавши метод математичної індукції, доведемо дану

гіпотезу.

Відповідно до першого кроку метода, який доводить лему 1,

одержимо, що Р{п = 1) = п

Лема

доведена.

Перейдемо до другого кроку - доведення леми 2.

Для цього припустимо відповідно до леми 2, що гіпотеза Р(п)

правильна для п-к. Тоді

Р(п =

к)=

+ 3 + ... + (2 к- 1 )

Доведемо тепер, що ця гіпотеза правильна й для

Р(п =

= 1 +

+ ... +

(2к- 1) + (2 (к+ 1) - 1)

{к+ І)

Подамо для цього Р(п = к

1) таким чином:

Р(п = к

1) = Р(п = к) + {2 (к+ 1)-1).

Тоді, оскільки Р(п = к) = к

Р(п =

1) =

+ 2 к+

=(Л+ І)

Результат співпадає з потрібним.

Гіпотеза підтверджена.

Приклад 2. Довести, що сума п перших чисел натурального

ряду

г./

і і

п(п +1)

Р(п) = 1

+... +

п = —

244

Розв'язання. У даному випадку неповну індукцію для

висунення гіпотези Р{п) виконувати не потрібно, оскільки вона задана

в умові прикладу.

Наведемо доведення леми

для даного випадку:

л =

!й±!)

і.

Таким чином, основа повної індукції одержана.

Доведення леми 2 має такий вигляд. Нехай

Р(п =

к)

= 1

2 + ... + к =

^~±.

Тоді відповідно до леми 2 потрібно одержати вираз

Р(п

1) = 1

...

кНк

1)=

{к + 1

к + 2)

Доведемо це. Дійсно,

Р(п =

+ \) = Р(п = к) + (к + 1) =

^^-

+ (к + \) =

_к

+Зк + 2

_(к

+ \)(к 4-

2 "" 2

Гіпотеза підтверджена.

Приклад 3. Довести, що сума квадратів перших чисел

натурального ряду

Розв'язання. У цьому прикладі, як і в прикладі 2, твердження

Р{п) задане у вигляді гіпотези, яка може перетворитися в істинне

твердження тільки після доведень лем 1 і 2.

Лема 1 доводиться шляхом підстановки 1 замість п:

245

6 6

Для доведення леми 2 припустимо, як і в попередніх прикладах,

що твердження Р(п) у випадку п-к справедливе, тобто для цього

прикладу

Доведемо, що справедливим буде також твердження, що

Р(п = к +

1) = І

+ 2

+ ... + к

+ (к +

І)

= Р{п = к) +

(к

І)

Для цього спочатку доведемо, що

Р(п -

к +

\)-Р(п

= *) =

(*+ І)

Дійсно,

Р(п

1)-Р(п=к)

_ + +^2)(2£ + 3) _ + ^^

^ =

2){2к

3) - к(2к

+1)]

+ 3* + Ак + 6

2к

А] =

~-[вк

+ 6] = (*

+1)

З доведеного далі випливає, що Р(п - к

1) = Р(п - к) + (к+ І)

Гіпотеза підтверджена.

Слід особливо підкреслити, що для правильного використання

метода математичної індукції обов'язково потрібно доводити обидві

леми І і 2, оскільки лема 1 є основою для проведення індукційних

кроків у методі, що розглядається, а лема 2 дозволяє виконувати

правильний перехід від випадку з п - к до випадку з п = к

1, який іде

за ним. Якщо лема 1 не доведена, то тоді відсутня основа для

проведення індукційних кроків. У результаті за допомогою леми 2

можна довести помилкову гіпотезу Р(п).

246

5. Вирави для самостійної роботи

1. Довести, що сума квадратів л перших непарних чисел

натуральної о ряду

Р(п) = І

+ З

...

+ (2л -1)

(2я -1)(2л + 1)

2. Довести, що сума кубів п перших чисел натурального ряду

Л») = 1

...

+ й

=''

л(,,+1)

3. Довести, що

4. Довести, що

ч , „ ^ ~ - , , ^ч п(п + 1)(л + 2)(л + 3)

Р(п)

= 1 • 2 • 3

+ 2

• 3 •

4 +...

л(л + 1)(л + 2) = ^ .

5. Довести, що

Р{гі)

• 1! + 2

•

2!+...+ л

•

п ! = (л + 1)! -1, де л ! = 1-2- ...

•

л.

6. Із 2л чисел 1, 2, ..., 2л довільно обрані (л + 1) чисел. Довести

твердження Р(п), що серед обраних чисел знайдуться хоча б два

числа, з яких одне ділиться на друге.

7. Довести, що п різних прямих, проведених на площині через

одну точку, ділять площину на 2л частин.

6. Історична довідка

Першим відомим ученим, який застосував метод математичної

індукції в сучасному вигляді в 1575 році, був італійський вчений

Франческо Мауроліко. У XVII столітті цей метод був удосконалений

П'єром де Ферма, який назвав його методом нескінченного спуску.

Він також використовувався Паскалем, зокрема, з метою доведення

формули для біноміальних коефіцієнтів.

До цього часу з допомогою метода математичної індукції було

виконано безліч різних доведень математичних теорем, і їх кількість,

безперечно, у майбутньому буде зростати.

247

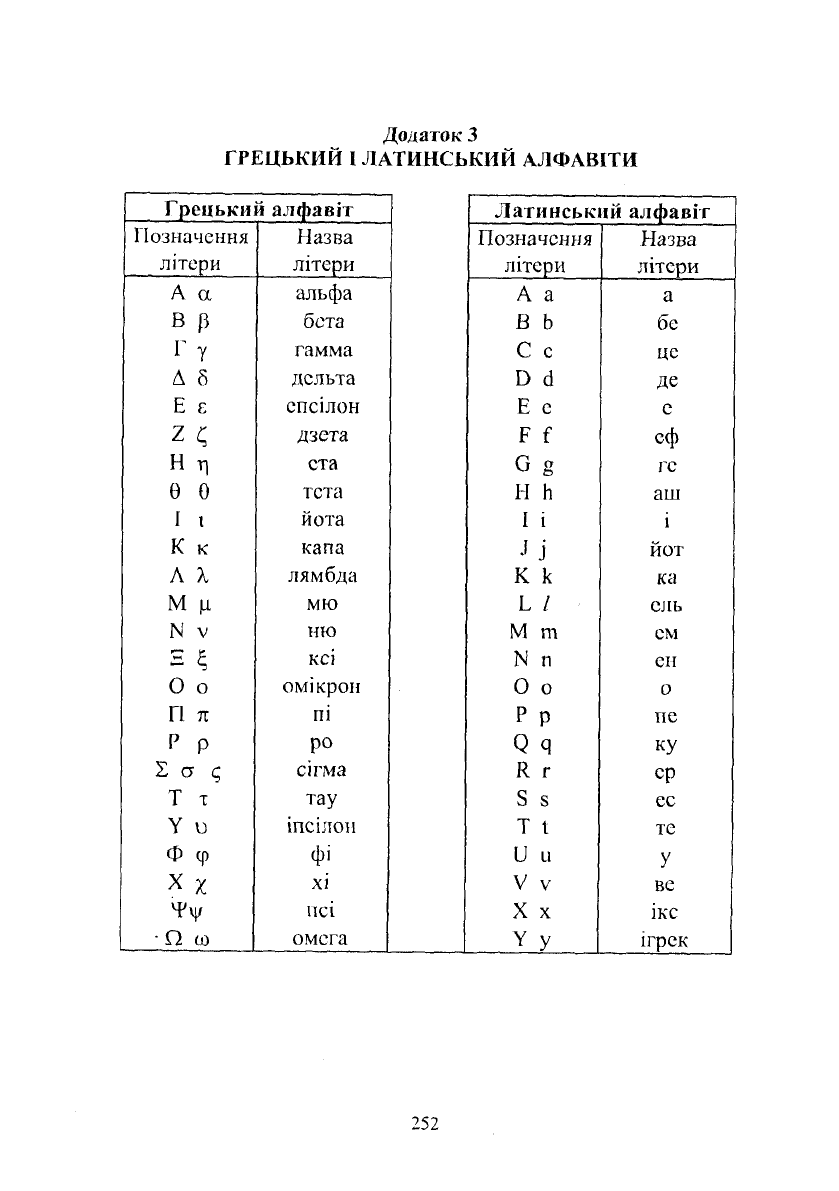
Додаток 2

ЕТИМОЛОГО-ТЕРМіНОЛОГІЧНИЙ СЛОВНИК

Основні означення

Термін

Етимологія

Значення

Абсолютний лат. аЬзоІиіш -

безвідносний, досконалий,

необмежений,

повний

безумовний

Алгебра

араб, аль джебр -

частина математики, наука про

відновлення

загальні операції над числами,

многочленами, векторами,

матрицями тощо

Аналогія гр. маАоуіа

подібність у будь - якому

відповідність,

відношенні

співрозмірність

Асоціативний

лат. амосіаііо -

приєднання,

об'єднання

сполучний

Біскція лат.

ЬІ5 —

двічі;

взаємно однозначна

іасіо - кидати

відповідність множин

Бінарний

лат. Ьіпагіиз -

подвійний

двійковий

Вектор лат.

Vес^о^

- той, що

величина, що характеризується

веде, несе

не лише числовим значенням,

Графік

Диз'юнкція

Дистрибутивний

гр. ураірікод-

накреслений

лат. (іі5іипсііо -

відокремлення,

розділення

лат. СІІЗІГІЬШІО -

розділення, розподіл

але й напрямком

зображення функції на

координатній площині

логічна операція поєднання

кількох висловлювань за

допомогою логічного

сполучника "АБО"

розподільний

248

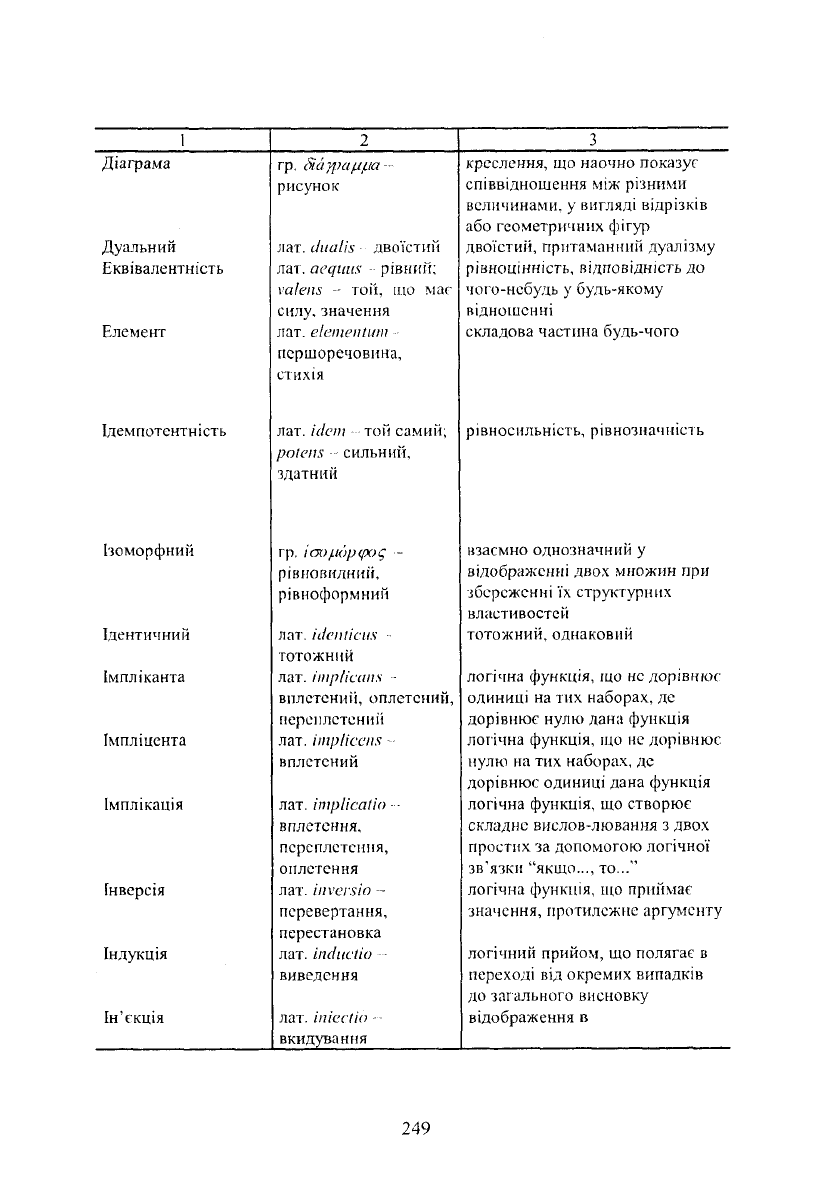
1 2

Діаграма

гр. Іхауращм--

креслення, що наочно показує

рисунок

співвідношення між різними

величинами, у вигляді відрізків

або геометричних фігур

Дуальний лат. сіиаііа двоїстий

двоїстий, притаманний дуалізму

Еквівалентність

лат. аедииа рівний; рівноцінність, ВІДПОВІДНІСТЬ ДО

\>а1еп$

~ той, що маг

чого-небудь у будь-якому

силу, значення

відношенні

Елемент лат. еіеіпеїш/т

складова частина будь-чого

першоречовина,

стихія

Ідемпотснтність

лат. ісіст той самий;

рівносильність, рівнозначність

роїепа сильний,

здатний

Ізоморфний

гр. Іоор6р<род -

взаємно однозначний у

рівновидний,

відображенні двох множин при

рівноформний

збереженні їх структурних

властивостей

Ідентичний

лат. іііешісих тотожний, однаковий

тотожний

Імпліканта

лат. іпір/ісап.ч -

логічна функція, що не дорівнює

вплетений, оплетений,

одиниці на тих наборах, де

переплетений

дорівнює нулю дана функція

Імпліцента

лат. ітріісепх -

логічна функція, що не дорівнює

вплетений

нулю на тих наборах, де

дорівнює одиниці дана функція

Імплікація

лат. ітріісаііо -

логічна функція, що створює

вплетення.

складне вислов-лювання з двох

переплетення,

простих за допомогою логічної

ОІТЛСТСННЯ

зв'язки "якщо..., то..."

Інверсія лат. іт'егзіо -

логічна функція, що приймає

перевертання,

значення, протилежне аргументу

перестановка

Індукція лат. іпсіисііо -

логічний прийом, що полягає в

виведення

переході від окремих випадків

до загального висновку

Ін'єкція лат. іпіссгіо

відображення в

вкидування

249

Інтуїція

лат. іпіиеог - уважно

безпосереднє осягнення істини

приглядатися

без логічного обгрунтування на

основі попереднього досвіду

Коефіцієнт

лат. соеДісіеіи

постійний множник при змінній

сприяючий

(невідомій)

Композиція лат. сотрозіїіо -

структура, побудова, послідовне

складання

використання

Компонент

лат. сотропеїи -

складова частина будь-чого

складова

Комутативний

лат. соттиіо

переставний

переставляти,

змінювати

Константа

лат. сопаїшк стала величина

постійний

Конституснта

лат. сопяіііиепх -

логічна функція, що встановлює

установлюючий

одиницю (або нуль) лише на

одному своєму наборі

Кон'юнкція лат. СОІІІШІСІІО -

логічна операція "І"

з'єднання, зв'язок

Координата

лат. со-(сит) величина, що визначає

разом, з

положення точки (вектора) у

огйіпШин

будь-якому просторі

упорядкований

Кортеж фр. сопете - упорядкований набір елементів

урочистий хід, виїзд

Логіка

гр. Лоуікбд - розумний

наука про закони й форми

мислення

Матриця

лат. таїгіх - джерело,

таблиця розташованих у вигляді

початок

прямокутника будь-яких

математичних об'єктів

Модуль

лат.

птсіиіи.н

- міра

абсолютна величина числа,

основа системи числення

Нейтральний лат. пеиігаїіиз

той, що не приєднається до

той, що не належить

жодної з протилежних сторін

ні до того, ні до

іншого

Оператор лат. орегаїог - той, що

відображення між елементами

діє

множин

Операція лат. арегаїіо дія

будь-яка дія, у тому числі

математична

Проекція

лат. ргоіесііо -

зображення будь-якого об'єкта

кидання вперед

на площині або прямій

Раціональний лат. юііопаїів -

цілі і дрібні числа, а також нуль

(про числа) розумний

250

2 3

Символ

гр. аиіфоЛоу - знак,

умовне позначення будь-якої

ознака

величини

Символ

гр.

т>/.фоЛо\>

умовне позначення будь-якої

знак, ознака

величини

Симетричний

гр. еющієтріа -

співрозмірний, маючий

співрозмірнісгь,

властивість симетрії

належна пропорція

Система

гр. аистцна - склад,

цілісне утворення, множина

упорядковане ціле

закономірно зв'язаних між

собою елементів у деяку єдність

Сюр'є.кція

лат. аирегіесііо відображення на

кидання зверху

Суперпозиція лат. хирегрохіїіп - накладання

спорудження

Тривіальний лат. Ігп'іаіія -

звичний, нсоригінальний

звичайний

Теорема

гр. вгмріию -

твердження, істинність якого

видовище, вчення

доводиться

Універсальний лат. шііуепаїіх -

загальний, різносторонній

загальний

Універсум лат. ШІІУЄГ.ЧШП -

загальна множина, для якої всі

всесвіт інші с підмножинами

Формула лат.[оппиіа - правило

математичне співвідношення

Функціонал

лат. /ІІІІСІІО

число, що с функцією від

виконання

функції

Функція

лат. (ипсНо

математична залежність однієї

виконання

змінної від іншої

251

252