Бордюженко О.М. Основи системного аналізу

Подождите немного. Документ загружается.

http://tbk.at.ua

Таблиця 6.3

Табличне значення критерію Фішера F

(рівень значимості Р=0,05)

Кількість ступенів свободи дисперсії адекватності f

ад

1 3 5 10 20 50 100

∞

1 161 216 230 242 248 252 253 254

2 18,1 19,2 19,3 19,4 19,4 19,5 19,5 19,5

3 10,1 9,3 9,0 8,8 8,7 8,6 8,6 8,5

4 7,7 6,6 6,3 6,0 5,8 5,7 5,7 5,6

5 6,6 5,4 5,1 4,7 4,6 4,4 4,4 4,4

10 5,0 3,7 3,3 3,0 2,8 2,6 2,6 2,5

20 4,4 3,1 2,7 2,4 2,1 2,0 1,9 1,8

100 3,9 2,7 2,3 1,9 1,7 1,5 1,4 1,3

∞

3,8 2,6 2,2 1,8 1,6 1,4 1,2 1,0

6.3. Статистичне планування експерименту

та побудова математичних моделей

Під статистичним (математичним) плануванням експерименту розуміють

постановку дослідів за попередньо складеною схемою, що володіє оптималь-

ними властивостями.

Статистичне планування дозволяє при мінімально можливій кількості до-

слідів вирішити задачу побудови математичної моделі у вигляді рівняння

регресії, що зв'язує вхідні і вихідні параметри.

Експеримент планується у відповідності з типовою матрицею, тобто таб-

лицею із

рядків та

стовпців, в якій приводиться набір комбінацій факто-

рів, симетрично варійованих відносно деякого початку координат або нульо-

вого (основного) рівня. Допустима область варіювання факторів (факторний

простір) вибирається на основі попереднього вивчення об'єкту у відповіднос-

ті з поставленою метою.

Для спрощення запису умов експерименту і обробки експериментальних

даних верхній рівень факторів кодується +1, нижній – 1, а основний 0.

Взаємозв'язок між натуральними Х

і кодованими х

значеннями факторів

визначається за формулою:

ioi

∆

−

, (6.15)

де

– натуральне значення фактора на нульовому рівні;

∆

– інтервал

варіювання фактора.

http://tbk.at.ua

Вид планування залежить від характеру досліджуваного явища. Якщо

можна апріорно передбачити прямолінійний зв'язок між параметрами в обра-

ній області варіювання факторів, застосовують планування на двох рівнях.

Воно дозволяє отримати модель у вигляді полінома першого ступеня для k

безрозмірних факторів х

xbby

∑

⋅+=

, (6.16)

де

– розрахункове значення вихідного параметру; b

і b

– вибіркові коефі-

цієнти регресії.

Однак задана точність розв'язків, навіть при дуже вузькому діапазоні змі-

ни факторів, за допомогою такої моделі досягається рідко. Поліноміальна

модель мусить найчастіше враховувати нелінійність впливу факторів на ви-

хід і явище синергізму

, тобто не прямо пропорційне посилення виходу при

одночасній зміні двох і більше факторів. Нелінійність враховується додаван-

ням до поліному першого порядку ще k елементів

iii

xb . В результаті отри-

мується модель головних ефектів другого порядку:

∑∑

++=

iiiii

xbxbby

. (6.17)

В цій моделі кожен фактор впливає на

квадратичною параболою.

Синергізм двох факторів враховується взаємодією

jiij

xxb

. Їх додавання

переводить модель у повний поліном другого ступеня:

∑∑∑

〈==

+++=

jiij

iiiii

xxbxbxbby

. (6.18)

Якщо всі квадратичні елементи b

iі

відсутні, але взаємодія залишається,

буде отриманий неповний поліном другого ступеня:

∑∑

〈=

++=

jiij

xxbxbby

. (6.19)

Для побудови лінійних і неповних квадратичних моделей використовують

повний факторний експеримент

(ПФЕ), планування якого здійснюється на

двох рівнях: верхньому (+1) і нижньому (−1). В цьому плані передбачені всі

можливі комбінації факторів на вказаних рівнях (планування типу 2

). В табл.

6.4 наведено приклади матриць ПФЕ для k = 2…4.

Для отримання повних квадратних моделей при досліджені нелінійних за-

лежностей застосовують плани другого порядку. При цьому кожен фактор

http://tbk.at.ua

планується не менше ніж на трьох рівнях: +1; 0; −1. Плани повних квадрати-

чних залежностей отримують шляхом додавання до ядра (тобто плану ПФЕ)

додаткових т.зв. "зіркових точок", а в деяких випадках і нульових з відповід-

ним інтервалом варіювання α.

Таблиця 6.4

Приклади добудови матриць ПФЕ для k = 2…4

Фактори

Точки

плану N

1 +1 +1 +1 +1

2 +1 -1 +1 +1

3 -1 +1 +1 +1

4 -1 -1 +1 +1

5 +1 +1 -1 +1

6 +1 -1 -1 +1

7 -1 +1 -1 +1

8 -1 -1 -1 +1

9 +1 +1 +1 -1

10 +1 -1 +1 -1

11 -1 +1 +1 -1

12 -1 -1 +1 -1

13 +1 +1 -1 -1

14 +1 -1 -1 -1

15 -1 +1 -1 -1

16 -1 -1 -1 -1

В практиці досліджень найчастіше застосовують ротатабельні плани, Бок-

са – Бенкіна, а також двох -, трьох -, чотирьох- (В

) та п'ятифакторні (В

і На

)

плани.

Матриці цих планів наведено у відповідній літературі [3, 4, 6, 15].

Для запобігання впливу систематичних похибок і для рівномірного розпо-

ділу чи усунення некерованих впливів на весь експеримент, досліди прово-

дять не за вказаним у матриці плану порядком, а в деякій випадковій (рандо-

мізованій) послідовності.

Результати дослідів обробляють за допомогою методів математичної ста-

тистики, згідно з якими обчислювальна процедура визначення коефіцієнтів

, b

та b

моделі побудована на основі методу найменших квадратів.

Розглянемо етапи отримання квадратичного рівняння з використанням

двохфакторного трьохрівневого плану (k=2; 11 точок плану).

1. Визначення коефіцієнтів рівняння регресії.

∑

⋅−⋅=

iiyTOTb

210

, (6.20)

)iy(Tb

i 3

, (6.21)

http://tbk.at.ua

()

∑

−−=

yii

OTiiyT)iiy(Tb

254

, (6.22)

()

ijyTb

ij 6

, (6.23)

де

;yO

∑

()

∑

⋅=

uiu

;yxiy

()

∑

⋅⋅=

ujuiu

;yxxijy

()

∑

⋅=

uiu

;y)x(ijy

де

– експериментальне значення вихідного параметру в точках u

…u

пла-

ну;

та

x – значення відповідно

-го та

-го факторів в u-ій точці плану;

значення параметрів( k=2 ):

=0,2632; T

=0,1579; T

= 0,1667; T

=0,5; T

= −0,1053; T

= 0,25.

2. Статистичний аналіз рівняння регресії.

Проведення експерименту завжди пов'язане з похибками внаслідок того,

що досліджувані залежності та процеси носять ймовірний характер, а отри-

мані рівняння не є їх точною копією, а лише відображенням з певним ступе-

нем ймовірності. Тому обов'язковим етапом при проведенні досліджень є

статистичний аналіз, основна мета якого – оцінка значимості коефіцієнтів

рівняння та перевірка адекватності рівняння.

Оцінка значимості коефіцієнтів рівняння регресії.

Дисперсію відтворюваності вихідного параметру знаходять за формулою:

−

∑

oou

)yy(

, (6.24)

де

y – значення вихідного параметру в u-ій нульовій точці; n

– кількість

нульових точок (в даному плані n

=3);

∑

– середньоарифметичне

значення вихідного параметру по нульовим точкам.

Середньоквадратичне відхилення вихідного параметру:

SS =

. (6.25)

http://tbk.at.ua

Середньоквадратичні похибки при визначенні коефіцієнтів :











⋅=⋅=

.S,S ;S,S

;S,S ;S,S

ybijybii

ybiybo

5062820

408305130

(6.26)

Далі визначають розрахункове значення критерія Ст'юдента

для кожно-

го коефіцієнта рівняння регресії:











===

;

t ;

bii

bij

ρρρ

. (6.27)

Коефіцієнти рівняння вважаються значимими, якщо розрахункове значен-

ня t

виявиться більше табличного t

, яке встановлюється [6, 15] в залежності

від заданого рівня значимості і кількості ступенів вільності f. Для даних умов

при рівні значимості P = 0,05 і

= n

−1=3−1=2 ,

=4,3.

Якщо коефіцієнт виявиться не значимим, він відкидається без перерахун-

ку решти. Коефіцієнти квадратичних членів залишають в рівнянні навіть,

якщо вони не значимі.

Перевірка адекватності отриманого рівняння регресії.

Дисперсія адекватності визначається за формулою:

()

−−−

−

∑

ад

nmn

)yy

(

, (6.28)

де

– розрахункове значення вихідного параметру в u-ій точці за отрима-

ним рівнянням регресії із значимими коефіцієнтами; m – кількість значимих

коефіцієнтів, в т.ч. b

Для оцінки однорідності дисперсій використовують критерій Фішера,

розрахункове значення

F якого визначають :

- при

ад

yад

F :SS =>

, (6.29)

- при

ад

yад

F :SS =<

. (6.30)

http://tbk.at.ua

Табличне значення критерія Фішера F

знаходять в залежності від прийн-

ятого рівня значимості і кількості ступенів вільності дисперсії адекватності

ад

f за табл. 6.3. При цьому:

)n(mnf

oад

−

. (6.31)

Рівняння вважається адекватним для прийнятого рівня довірчої ймовірно-

сті, якщо F

< F

. Якщо виявилось, що дане рівняння неадекватне, то при

проведенні дослідів були допущені грубі помилки, або вибраний поліном

недостатньо повно відображає дослідну залежність. В таких випадках необ-

хідно або повторити досліди, або змінити інтервали варіювання, або застосу-

вати інший план.

6.4. Аналіз та використання математичних

(експериментально-статистичних) моделей

Коефіцієнти повної квадратичної моделі (6.18) характеризують ступінь

впливу факторів на вихідний параметр Y. В математичній теорії експеримен-

ту такий "ступінь впливу" носить назву ефекту фактора

Розрізняють три види ефектів:

1) лінійний

або головний ефект, що чисельно рівний абсолютному зна-

ченню коефіцієнта b

;

2) квадратичний

ефект, що чисельно рівний b

і характеризує нелінійність

моделі по фактору x

;

3) ефект взаємодії

, рівний b

, який характеризує спільний вплив на Y двох

факторів

та

Коефіцієнт b

, як вільний член рівняння, тотожньо рівний розрахунковому

значенню

в центрі факторного простору ( y

= b

, при

=0,

k,1

) .

Аналіз індивідуального впливу факто-

рів здійснюється шляхом оцінки впливу

на Y кожного з факторів x

після розташу-

вання решти факторів на певних функціо-

нально зв'язаних(x

=ƒ(x

)), або стабільних

рівнях (x

=const). Фактори можна стабілі-

зувати як на рівнях, на яких ставився екс-

перимент, тобто −1; 0; +1, так і на рівнях,

що відповідають двом екстремальним то-

чкам моделі. В останньому випадку аналіз

буде найбільш інформативним, оскільки

він проводиться в максимально контраст-

них умовах.

Після закріплення всіх факторів, крім

Рис. 6.1. Парабола, як геомет-

ичний образ однофакторної

моделі другого порядку

1ex

http://tbk.at.ua

одного, на певних рівнях модель (6.18) прийме вигляд однофакторної моделі

другого порядку (6.32), що представляє собою параболу з екстремумом Y

ех

, в

точці x

1ех

(рис. 6.1):

11111

xbxbby

⋅+⋅+=

, (6.32)

42 b

;

oexex

−=−=

, (6.33)

Абсолютне чисельне значення коефіцієнта b

показує швидкість зміни Y в

залежності від фактору

. Знак при коефіцієнті показує характер впливу: "+"

свідчить при те, що із збільшенням

величина Y зростає, "−" – про те, що

зменшується. Чим більше значення коефіцієнта, тим сильніший вплив факто-

ра.

Величина квадратичного коефіцієнту b

характеризується прискоренням

зміни Y при зміні

і, разом з b

(в залежності від їх знаків), повністю визна-

чає форму параболи.

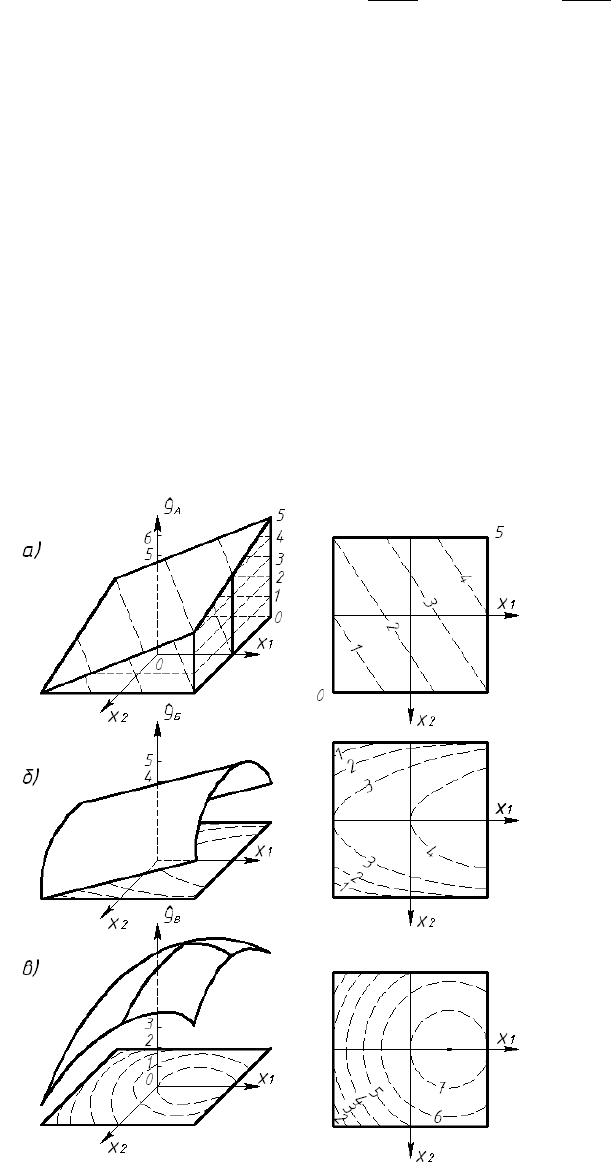
Двохфакторна модель другого порядку має вигляд (6.34) і в залежності від

наявності коефіцієнтів b

та b

представляє собою одну з поверхонь друго-

го порядку (рис. 6.2).

2112

222

1112211

xxbxbxbxbxbby

+⋅+⋅+⋅+⋅+=

. (6.34)

Абсолютне числове значен-

ня коефіцієнту взаємодії b

по-

казує наскільки зміниться шви-

дкість зростання

в залежнос-

ті від

, якщо фактор

змі-

ниться від 0 до |1|. Знак "+" пе-

ред b

свідчить про те, що збі-

льшення вихідного параметру

можливе лише якщо x

і x

зна-

ходяться однозначно на верх-

ньому або нижньому рівні, а

знак "−" дасть збільшення Y,

якщо фактори знаходяться на

протилежних рівнях .

Проекція поверхні двох фак-

торної моделі Y на площину

факторів x

і x

зображується у

вигляді ліній однакового виходу

(ізоліній) (рис. 6.2). В усіх точ-

ках таких ліній вихід Y має по-

стійне значення Y

незалежно

Рис. 6.2. Геометричні образи поверхонь

другого порядку

http://tbk.at.ua

від координат x

і x

. Таким чином, якщо заданому набору координат x

і x

відповідає одне значення Y, то одному заданому Y може відповідати множи-

на x

і x

, що лежать на ізолінії.

Принцип побудови ізоліній аналогічний побудові висотних ліній (ліній

однакових висот) на топографічних картах.

Деякі типові двохфакторні ситуації зображені на рис. 6.2.

Для побудови ізоліній необхідно вибрати декілька перерізів факторного

простору з відповідними значеннями

, задатися рядом значень одного з

фактора x

і розв'язати зведене квадратичне рівняння типу (6.32) відносно

фактора

по цим значенням. Після цього отримати точки ізоліній сполуча-

ють плавними кривими.

За допомогою математичних моделей (рівняння регресії) можна вирішу-

вати ряд задач :

 інтерполяційні (дозволяють знайти значення Y в межах області

варіювання факторів від −1 до +1 при будь-яких значеннях фак-

торів);

 екстраполяційні (дозволяють прогнозувати значення Y за межами

області варіювання при

> |1|);

 оцінки ролі факторів (за абсолютними величинами коефіцієнтів);

 регулювання (полягають у визначені такого поєднання факторів,

яке забезпечує задані показники вихідного параметру);

 оптимізаційні (полягають у визначенні такого поєднання факто-

рів, що забезпечують максимальне (мінімальне) значення Y –

критерію ефективності при заданих обмеженнях);

 мінімізаційні (визначають таке співвідношення факторів, при

якому забезпечується задане значення Y при мінімальному зна-

ченні даного з факторів);

 аналітично-геометричні (на основі рівняння регресії будують

графічні залежності та номограми для Y в межах області варію-

вання факторів, що дозволяють оперативно визначити значення Y

при різноманітних поєднаннях факторів).

http://tbk.at.ua

Тема 7. БУДІВЕЛЬНЕ ПІДПРИЄМСТВО ЯК СОЦІАЛЬНО-

ВИРОБНИЧА СИСТЕМА

4.1. Системний підхід в управлінні підприємством

Будівельне підприємство відноситься до соціально- вироб-

ничих систем, які характеризуються тим, що складовою частиною цієї

системи, головним і найбільш активним елементом у виробничому і соціаль-

ному процесах є людина.

В процесі функціонування будь-яка соціально-виробнича система з часом

змінює свій стан, який описується множиною різних факторів як зовнішнього

так і внутрішнього середовища цієї системи.

З метою оптимального управління такими системами та досягнення зада-

них кінцевих результатів їх описують за допомогою кібернетичних моделей

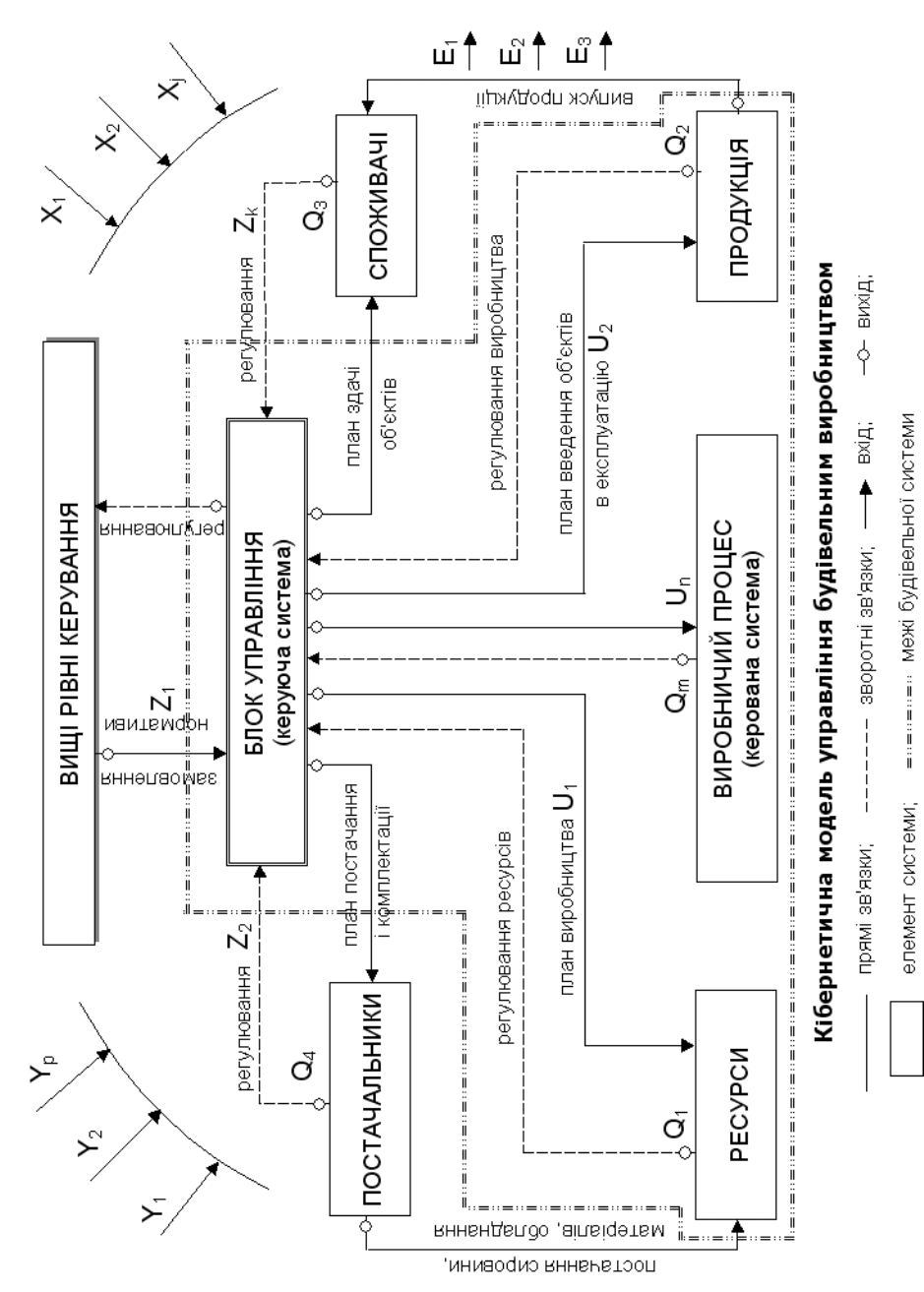
На рис. 7.1 показана кібернетична модель системи управління будівель-

ним підприємством (виробництвом).

Кожний елемент системи характеризується вибором параметрів, що

визначають його стан. Параметр стану змінюється під дією вхідного сигналу,

що надходить через вхідні канали (входи), а зміна стану елементу приводить

до утворення вхідних сигналів, які передаються через вихідні канали (вихо-

ди) на інші елементи системи. Зовнішні дії на будівельну систему (Z

, Z

, ... ,

– входи в систему) проявляються у вигляді замовлень, контрактів, догові-

рних умов, нормативів, що приводить до зміни параметрів елементів.

Блок управління формує керуючі команди у вигляді планових завдань U

, ..., U

. Зміни параметрів елементів системи Q

, Q

, ...,Q

передаються на

блок управління по зворотньому зв'язку.

На стійкість параметрів елементів будівельної системи впливають харак-

теристики регіональних умов будівництво (виробництво) Y

, Y

,...,Y

, а та-

кож випадкові фактори невизначеності Х

, Х

,...,Х

, які створюють активний

вплив зовнішнього середовища. Тому виробничі системи завжди є від-

критими.

Ефективність управління системи по випуску готової будівельної продукції

може характеризуватись різними критеріями: Е

, Е

,..., Е

(наприклад, кількіс-

тю, собівартістю, прибутком і т.п.). Таким чином, в загальному вигляді ефекти-

вність функціонування системи може бути виражена у вигляді рівняння:

,…Z

; Y

,….Y

; U

,…,U

; Q

,…Q

)

(7.1)

В процесі управління на систему будуть впливати фактори невизначено-

сті

, Х

,..., Х

, які описують динамічну зміну умов виробництва

(наприклад, зміну технологічних режимів, зриви постачання матеріалів, різні

Поняття "кібернетика" розглядалось в п.1.1.

http://tbk.at.ua

Рис. 7.1.