Бондаренкова И.В. Метрология, стандартизация и сертификация

Подождите немного. Документ загружается.

Федеральное

агентство

по

образованию

Государственное

образовательное

учреждение

высшего

профессионального

образования

САНКТ

-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ

УНИВЕРСИТЕТ

РАСТИТЕЛЬНЫХ

ПОЛИМЕРОВ

И.В.Бондаренкова,

Г.А.Кнодель,

И.С.Ковчин,

Г.А.Кондрашкова

МЕТРОЛОГИЯ,СТАНДАРТИЗАЦИЯ

СЕРТИФИКАЦИЯ

Учебно-методическое

пособие

Санкт-Петербург

2009

_-_

_._-_._-'---

",.,,,

НАУЧНО-ИНФОРМАЦИОННЫЙ ЦЕНТР САНКТ-ПЕТЕРБУРГСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

УДК

658.562:006.83

Метрология,

стандартизация

септификация:

учебно-методическое

посо

бие

сост.

И.В.Бондаренкова,

ГАкнодель,

и.с.Ковчин,

Г.А.кондрашкова

гаувпа

СПб

ГТУ

РП.

СПб.,

2009.

- 68

с.

Учебно-методическое

пособие

содержит

необходимые

теоретические

сведения

задания

для

выполнения

практических

занятий

по

дисциплине

«Метрология,

стандартизация

сертификация».

Предназначено

для

студен

тов,

обучающихся

по

направлениям

220200

«Автоматизация

управление»,

240100

«Химическая

технология

биотехнология»

280~00

«Защита

окру

жающей

среды»

всех

форм

обучения.

Рецензенты:

профессор

кафедры

АПХП

гау

впа

«Санкт

Петербургский

технологический

институт

(технический

универсигет)»,

д-р

техн.наук

Л.А.Русинов;

заведующий

кафедрой

АЗиЗ

ГО'У

НПО

«Санкт-Петербургский

государствен

ный

технологический

университет

растительных

полимеров»,

д-р

техн.наук,

профессор

в.д.Кулик.

Подготовлено

рекомендовано

печати

кафедрой

информационно

измерительных

технологий

систем

управления

ГОУ

впа

СПБГТУРП

(про

токол

от

04.06,2009

г.).

Утверждено

изданию

методической

комиссией

факультета

АСУТП,

том

впа

СПБГТУРП

(протокол

от

08.06.2009

г.).

Рекомендовано

изданию

Редакционно-издательским

советом

универси

тета

качестве

учебно-методического

пособия.

гау

впа

Санкт-Петербургский

государственный

технологическИЙ

университет

растительных

полимеров,

2009

Бондаренкова

и.в.,

кнодель

Г.А.,

Ковчин

И.С.,

Кондрашкова

Г.А.

Введение

Настоящее

учебно-методическое

пособие

предназначено

для

стулентов,

обучающихся

по

направлениям

220200,

240100

280200

включает

себя

де

сять

практических

занятий

по

разделам

дисциплины

«Метрология,

стандарти

зация

сертификация».

Предусмотрено

несколько

вариантов

заданий,

что

по

зволяет

выполнять

их

как

всей

группе

студентов,

так

индивидуально

по

ва

риантам,

задаваемым

преподавателем.

Практические

задания

выполняются

использованием

персональных

компьютеров.

Для

выполнения

практических

заданий

студенты

должны

прослушатъ

лек

ционный

курс

по

соответствующему

разделу

и изучить

дополнительный

учеб

ный

материал

по

литературным

источникам,

список

которых

приведен

конце

настоящего

учебно-методического

пособия.

процессе

решения

заданий

не

обходимо

пользоваться

справочными

таблицами

соответствующими

стан-

дартами.

Отчеты

по

выгюлненным

заданиям

необходимо

сдать

преподавателю.

Текст

задания

может

быть

выполнен

от

руки

или

машинным

способом.

Все

необходимые

графики

схемы

следует

вычерчивать

масштабе

применени

ем

инструментов

или

выполнять

пом,?щью

любого

графического

редактора

на

персональном

компьютере.

Цели

задачи

практнческнх

занятий

Целью

про

ведения

практических

занятий

по

дисциплине

«Метрология,

стандартизация

сертификация»

является

углубление

закрепление

теорети

ческого

материала,

приобретение

знаний

назначении

возможности

приме

нения

основных

правил

документов

системы

сертификации,

об

обеспечении

необходимого

уровня

качества

продукции

услуг

на

базе

стандартизации и

сертификации,

порядке

сертификации

сырья,

готовой

продукции

техноло

гического

процесса

производства.

Задача

проведения

практических

занятий

заключается

ознакомлении

сту

дентов

правилами

определения

погрешностей

результатов

средств измере

ний,

проведения

поверки

средств

измерений,

основными

нормативными

доку

ментами,

регламентирующими

деятельность

области

стандартизации

сер

тификации,

изучении

их

основных

положений,

также

изучении

исполь

зовании

различных

методов

статистического

контроля

качества.

TalC8Jl

градуировка

ртутных

термометров

осуществлялась

прошлом,

когда

качестве

единицы

И'3мереНИI

темперпуры

нспользовался

"Ц.

Прн

современных

температурных

шкалах,

основанных

на

объемном

расширении

веществ

dT=

kdV,

где

V-

объем

вещества,

температурный

коэффициент

рас

ширеняя

вещества,

ртутные

термометры

градуируются

по

образцовым

манометрическнм

термометрам.

Это

связано

тем,

что

значение

завнсит

от

интервала

измеряемых

температур,

т.е,

шкалы

Р1УГных

тер

яоиетров

нелинейны,

Использование

манометрических

термометров

обеспечивает

адекватность

'с н

как

единицы

измерения

температуры

их

перевода

учетом

разницы

реперных

точках,

Т.е.

[К]

['с]

+273,15

К.

Построение

градуировочной

характеристики

предполагает

две

возмож

ности.

Первая

из

них

заключается

том,

что

зависимость

между

входным

воз

действием

откликом

на

него

известна

(например,

линейная,

квадратичная,

логарифмическая

т.п.),

но

нензвестны

коэффициенты,

входящие

соответст

вующее

алгебраическое

уравнение.

Вторая

возможность

состоит

необходи

мости

аппроксимации

экспериментальных

данных

аналитической

зависимо

стью.

Если

вид

градуировочной

характеристики

= f(X),

где

входная

вели

чина,

выходная

величина,

известен,

то

задача

состоит

том,

чтобы

в её

представлении

полиномом

соответствующей

степени:

найти

такие

значения

коэффициентов

о,а"а

' ·

при

которых

эта

зависи

мость

наилучшим

образом

соответствовала

бы

экспериментальным

данным.

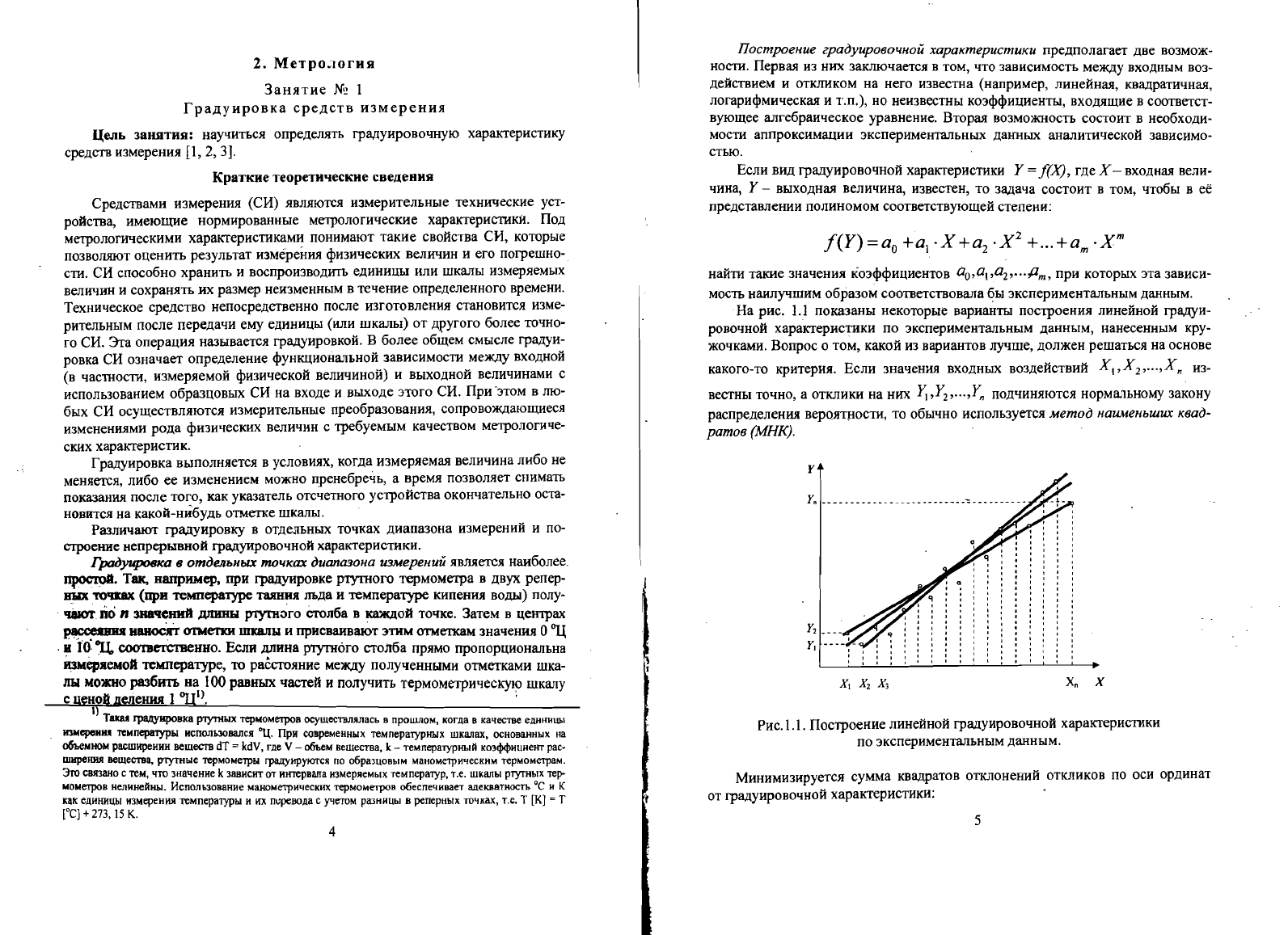
На

рис.

1.1

показаны

некоторые

варианты

построения

линейной

градуи

ровочной

характеристики

по

экспериментальным

данным,

нанесенным

кру

жочками.

Вопрос

том,

какой

из

вариантов

лучше,

должен

решаться

на

основе

какого-то

критерия.

Если

значения

входных

воздействий

Х"Х

,Х

из

вестны

точно,

отклики

на

них

~'Y2'''''Yn

подчиняются

нормальному

закону

распределения

вероятности,

то

обычно

используется

метод

наименьших

квад

ратов

(МНК).

• . . . . . . . .. ... .

РИС.1.1.

Построение

линейной

градуировочной

характеристики

по

экспериментальным

данным.

Минимизируется

сумма

квадратов

отклонений

откликов

по

оси

ординат

от

градуировочной

характеристики:

Таблица

1.1.

Экспериментальные

данные

Коэффициенты

ао,а]

,а2

,...,

аm,

определяющие

оптимальную

по

крите

рию

наименьших

квадратов

градуяровочную

характеристику,

находятся

из

ус

ловия

равенства

нулю

производных

от этой

суммы

по

каждому

коэффициенту.

4 5

8 9

12 13

Х;

104 120 139

IS4 180 208 241 250 269

301

У;

8 10

15 20 19 23

26 30 31

30 37

-'1,

.е,

-LУi

=У;

;=1

1 13

г:

-2,Х=Х;

13 ;=1

-:2:

;

13 ;=1

1 13

...!:-

Х.

ху

;=1'

2,(1';

-ао

-QI'

Х;);:

О;

;=1

~).

ао

аl

Х)

Х;

о.

\.;=1

Два

уравнения

двумя

неизвестными

имеют

единственное

решение.

Разделив

левую

правую

части

каждого

уравнения

на

13,

введя

обозначе-

ния:

(1.1)

I(r;

-й

Х;

-й

х;

...

х;m)2

=min

i=l

При

мер

При

градуировке

измерительного

прибора

линейной

градуировочной

характеристикой

получены

числовые

значения

экспериментальных

данных,

представленные

табл.Ы:

Найти

методом

наименьших

квадратов

аналитическое

выражение

для

гра

дунровочной

характеристики

и построить

её

графически.

Решение

Линейная

градуяровочная

характеристика

описывается

выражением:

+й!·Х,

где

коэффициенты

й!

методом

наименьших

квадратов

находятся

из

ус

ловия:

(1';

ао

а,

х)2

= min

;=1

где

-г-;

номер

опыта.

где

У,

х,

ХУ

оценки

среднего

значения.

Получим

выражение

для

коэффнциентов

ао

й\

форме,

выходящей

по

своему

значению

за

рамки

частного примера:

ХУ

х.у

р2_

(

Вышеприведенная

функция

минимальна

точке,

где

ее

ПРОИЗВОД1!ые

по

ао

аl

равны

нулю.

Поэтому

коэффициенты

определяются

ре

зультате

решения

системы

уравнений:

рассматриваемом

случае

ао

= 0.7;

а]

= 0.124,

так что

аналитическое

выражение

для

градуировочной

характеристики

имеет

вид:

У=

0,7 +

0,1211·х

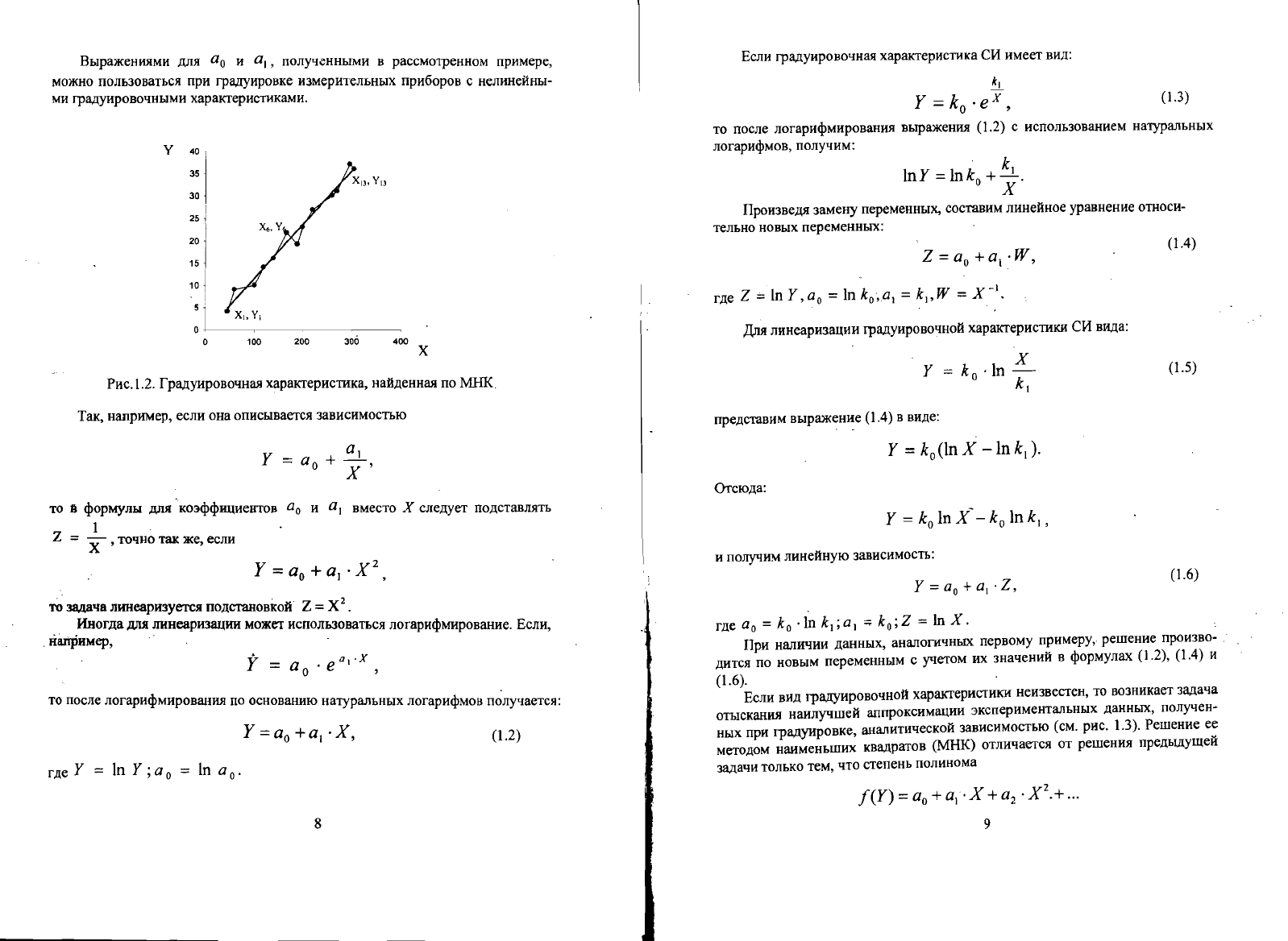
Графически

она

построена

на

рис.l.2,

где

точк~ми

нанесены

эксперимен

тальные

данные.

lnY

=:;lnk

+_1

Произведя

замену

переменных,

составим

линейное

уравнение

относи

тельно

новых

переменных:

Если

градуировочная

характеристика

СИ

имеет

вид:

У:::

.еХ,

(1.3)

то

после

логарифмирования

выражения

(1.2)

использованием

натуральных

логарифмов,

получим:

для

линеаризации

градуировочной

характеристики

СИ

вида:

(1.5)

(1.4)

·ln-

=а

+Q1'W,

I "

где

;;;

У,

=ln k

W =

-1.

40 "

251

201

100

200

300

400

Выражениями

для

а.,

полученными

рассмотренном

при

мере,

можно

пользоваться

при

градуировке

измерительных

приборов

нелинейны

ми

градуировочными

характеристиками.

Рис.г.З.

Градуировочная

характеристика,

найденная

по

МИК

Так,

например,

если

она

описывается

зависимостью

представим

выражение

(1.4)

виде:

(1.6)

получим

линейную

зависимость:

Отсюда:

ЛУ)

+a1·X

+а

·Х

...

где

= k

·ln

;

I ::;: k

;Z =ln

Х.

При

наличии

данных,

аналогичных

первому

примеру,

решение

произво

дится

по

новым

переменным

учетом

их

значений

формулах

(1.2), (1.4)

(1.6).

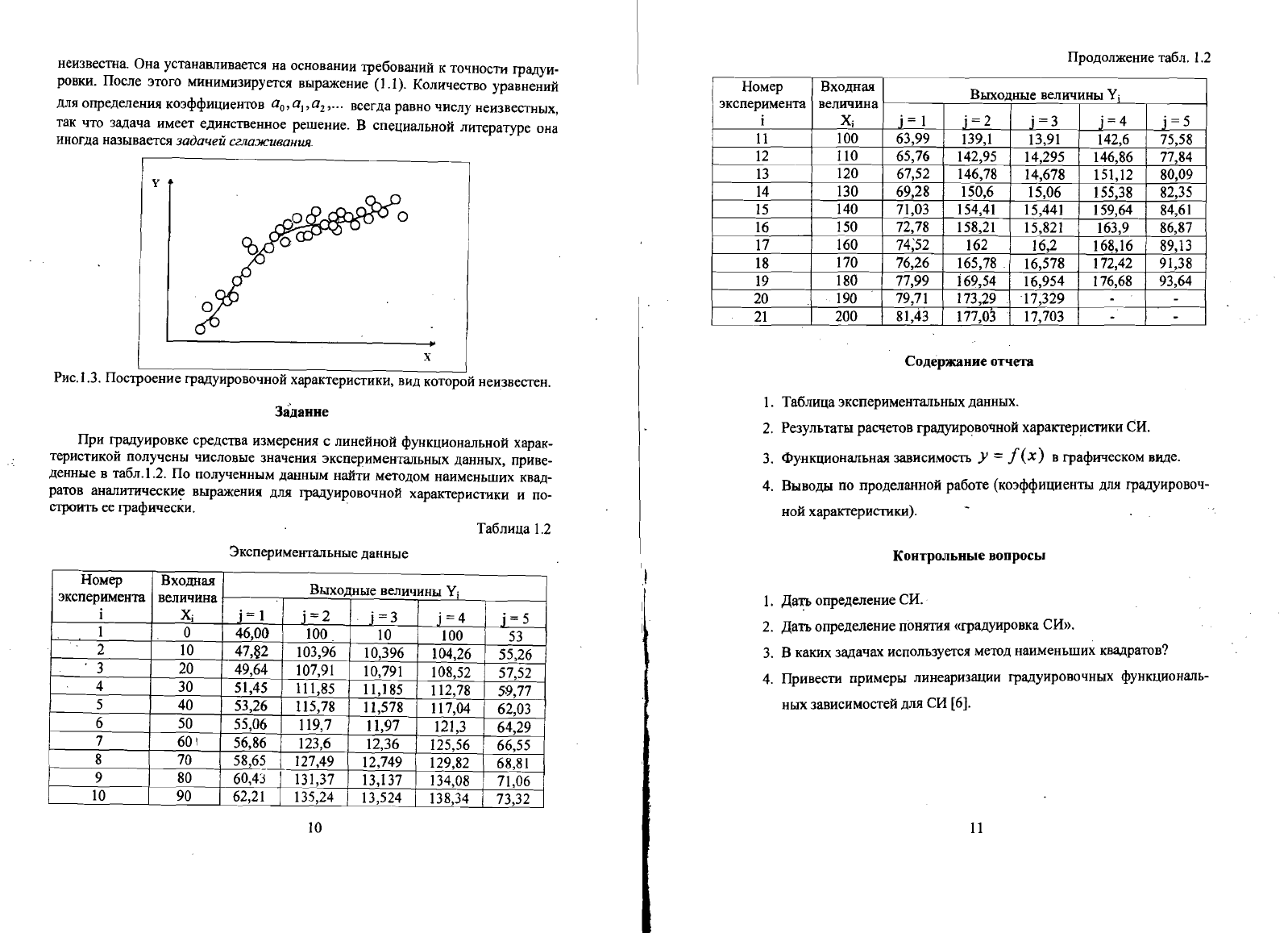
Если

вид

градуировочной

характеристики

неизвестен,

то

возникает

задача

отыскания

наилучшей

аппроксимации

экспериментальных

данных,

получен

ных

при

градуировке,

аналитической

зависИМОСТЬЮ

(см.

рис.

1.3).

Решение

ее

методом

наименьших

квадратов

(МИК)

отличается

от

решения

предьщущей

задачи

только

тем,

что

степень

полинома

(1.2)

=:;

+_1

Ох'

то

формулы

для

'коэффициентов

а,

вместо

следует

подставлять

Z = х'

точно

так

же,

если

то

после

логарифмирования

по

основанию

натуральных

логарифмов

получается:

где

=ln

У;

= ln

о'

1'0

задача

линеаризуется

подстановкой

Z =

2 •

.Иногда

для

линеаризации

может

использоваться

логарифмирование.

Если,

нвпример,

неизвестна.

Она

устанавливается

на

основании

требований

точности

градуи

ровки.

После

этого

минимизируется

выражение

(Гл).

Количество

уравнений

для

определения

коэффициентов

о,а

ра

· ·

всегда

равно числу

неизвестных,

так

что

задача

имеет

единственное

решение.

специальной

литературе

она

иногда

называется

задачей

сглаживания.

Рис.Т.З.

Построение

градуировочной

характеристики,

вид

которой

неизвестен.

Заданне

При

градуировке

средства

измерения

линейной

функциональной

харак

теристикой

получены

числовые

значения

экспериментальных

данных,

приве

денные

таБЛ.l.2.

По

полученным

данным

найти

методом

наименьших

квад

ратов

аналитические

выражения

для

градуировочной

характеристики

по-

строить

ее

графически.

Таблица

1.2

Экспериментальные

данные

Номер

Входная

Выходные

величины

У.

эксперимента

величина

х,

j=1

j=2

j=3

j=4

j = 5

46,00

]00

100

4Ц2

103,96

10,396

104,26

55,26

49,64

107,91

10,791

108,52

57,52

51,45

111,85 11,] 85

112,78

59,77

53,26

115,78

11,578

117,04

62,03

55,06

119,7

11,97

121,3

64,29

601

56,86

123,6

12,36

125,56

66,55

8 70

58,65

]27,49

12,749

129,82

68,81

60,43

131,37

13,137

134,08

71,06

62,21

135,24

13,524

138,34

73,32

Продолжение

табл.

1.2

Номер

Входная

Выходные

величины

У.

эксперимента

величина

i = 1

j=2

j=3

j=4

j = 5

100

63,99

139,1

13,91 142,6 75,58

110

65,76

142,95

14,295

146,86

77,84

120

67,52

146,78

14,678 151,12 80,09

14 130

69,28

150,6

15,06

155,38

82,35

140

71,03 154,41

15,441 159,64 84,61

150 72,78 158,21

15,821 163,9 86,87

17 160 74;52 162

16,2

16~,16

89,13

170

76,26

165,78

16,578

172,42 91,38

180 77,99

i69,54 16,954 176,68 93,64

190 79,71

173,29

17,329

200

81,43 177,03

17,703

- -

Содержание

отчета

Таблица

экспериментальных

данных.

Результаты

расчетов

градуировочной

характеристики

си.

Функциональная

зависимость

(х)

графическом

виде.

Выводы

по

проделанной

работе

(коэффициенты

для

градуировоч

ной

характеристики).

Контрольные

вопросы

Дать

определение

си.

Дать

определение

понятия

«градуировка

си».

каких

задачах

используется

метод

наименьших

квадратов?

Привести

примеры

линеаризации

градуировочных

функциональ

ных

зависимостей

для

си

[6].

для

случайных

составляющих

погрешностей

как

геометрическая

сумма:

для

систематических

составляющих

погрешностей

формула

(2.1)

рас

сматривается

как

алгебраическая

сумма

погрешностей

результатов

прямых

измерений:

Занятие

N!!

Анализ

погрешностей

результатов

косвенных

измерений

Цель

занятия:

научиться

оценивать

погрешности

косвенных

измерений

физических

величин

сформулировать

требования

точности

измерений

не

посредственно

измеряемых

величин

аргументов

функциональной

зависимо

сти

результатов

косвенных

измерений

от

прямых

измеряемых

величин

[1, 2,

3].

Lb;

'бх,с,

1=1

(2.2)

Краткие

теоретические

сведения

(2.7)

(2.3)

jд

сх

j=l

2 n

ДZ

= L

Ь;2

Дх,.

, ;=1

Случайные

погрешности

суммируются

по

правил

сложения

дисперсий:

или

'д

..+<:

.в,

'д

)

(2,6)

j=1

Видно,

что,

отличие

от

предьщущего

случая,

когда

суммировались

аб

солютные

погрешности,

здесь

суммируются

относительные

погрешности.

Систематические

относительные

составляющие

суммируются

со

своими

зна-

ками

учетом

знаков

показателей

С/

Немного

сложнее

случай,

когда

искомая

величина

выражается

виде

произведения

Z =

X~'

X~2

.....

Х:·.

Это

произведение

сначала

логарифмируют

и только после

этого

переходят

дифференЦиалам,

получая:

(2.i)

или

При

косвенных

измерениях

значение

искомой

величины

вычисляют

по

резуль!атам

прямых

измерений

других

величин

Х;,

функционально

связанных

искомой.

Функциональная

зависимость

Z(X/. X

Хз

...

Х,J,

как

правило,

за

дается

виде

формулы.

Обычно

рекомендуют

провести вначале

обработку

результатов

каждого

из

прямых

измерений,

затем

по

полученным

оценкам

центров

распределений

величин

Х;

вычислить

оценку

искомой

величины

и,

наконец,

по

оценкам

по

грешностей

оценок

Х;

вычислить

оценку

погрешностей

окончательного

ре-

зультата,

как

будет

описано

ниже.

Но

для

оценивания

случайной

составляющей

погрешности

результата

возможен

другой

путь:

многократно

повторить

процедуру,

состоящую

из

однократных

измерений

всех

Х;

вычисления

получить

таким

образом

вы

борку

значений

со

статическим

разбросом

обработать

ее

стандартным

спо

собом.

Достоинство

этого

метода

состоит

том;

что

он

не

требует

знания

ха

рактеристик

составляющих

случайной

погрешноети,

экспериментатор

имеет

дело

Сразу

их

суммой.

Тем

не

менее, его

применяют

реже.

Поэтому

вернемся

задаче

вычисления

оценки

погрешности

окончательного

результата

по

оцен

кам

погрешностей

непосредственно

измеренных

величин

Х,

Поскольку

погрешности

этих

величин

предстоит

суммировать,

удобно

характеризовать

их

оценками

СКО

8/. .

Наиболее

простая

функциональная

зависимость

линейная

комбинация

Ь/

Х/

Ь2Х2

+...

+Ь"Х".

Переходя

дифференциалам

как

аналогам

малых

погрешноетей,получаем:

=Ь/:-"Х

+Ь

2д

+"'+Ьnд

I 2

1'11"

где

I '

,,,.

абсолютные

погрешности

прямых

измерений

аб

солютная

погрешностъ

косвенного

результата

измерения.

= [(0,05)2+

(0;05)2

+ (0,01

)2]

1/2

± 0,07 %.

где

ИХ

падение

напряжения

на

Используя

формулы

(2.7)

(2.8),

получим

выражение

для

систематиче-

ских

случайных

составляющих

погрешностей

косвенного

измерения

Отсюда

можно

утверждать,

что

погрешность

измерения

сопротивления

-о

<о

находится

пределах

Rxc

или

-0,06

% <

< + 0,08 % .

(2.13)

(2.12)

(2.11

)

(2.1

О)

R =

Их

.н

И'

06р,

обр

я,

обр

о б

06р

Откуда

искомое

сопротивление

вычисляют

по

зависимости:

S: =

•

Rx c

ИхС

RобрС

dOP

, =

:S;

±O,Ol %,

06р

02 02

б»,

=OUx+OU<Ap+OR<Ap,

где

систематическая и

случайная

составляющие

погрешно-

сти

измерения

соответственно.

Основная

статическая

погрешность

потенциометра

±О

,05 %,

образцовое

манганиновое

сопротивление

а6р

известно

погрешностъю

Rc6p =

±О,О1

тогда:

Отметим

особенность

косвенных

измерений,

заключающуюся

том,

что

нельзя

для

каждого

возможного

значения

заранее

оценить

инстру

ментальную

погрешность

(как

это

делается

при

прямых

измерениях).

Дело

том,

ЧТО

одно

то

же

значение

может

быть

получено при

различных

сочетаниях

непосредственно

измеряемых

величин,

значит,

при

различных

погрешностях

их

измерения.

Получив

окончательный

результат

отбросив

промежуточные

данные,

экспериментатор

уже

не

может

восстановить

исход

ное

сочетание

величин

Х}

Это

особенность

была

не

очень

заметной,

пока

результаты

косвенных

из

мерений

обрабатывались

вручную.

Но

при

переходе

автоматизированным

экспериментальным

установкам

измерительным

информационным

системам

(ИНС)

невозможность

их

метрологической

аттестации

по

образцу

простых

приборов

стала

вызывать

определенные

трудности.

Для

их

преодоления

при

шлось

возложить

оценивание

погрешностей

косвенных

измерений

на

вычис-

лительные

средства,

входящие

состав

самих

ИИС.

Были

разработаны

норма

тивные

документы,

согласно

которым

оценки

погрешностей

косвенных

изме

рений

должны

вычисляться

для

каждого

получаемого

результата

параллельно

вычислениями

самого

этого

результата.

Для

вычисления

оценок

погрешно

стей

должны

быть

предусмотрены

специальные

программы.

Следует

подчеркнуть,

что,

исходя

из

зависимостей

2.1 - 2.8,

можно

сфор

мулировать

требования

точности

измерения

непосредственно

измеряемых

величин

Х;

которые

связаны

искомым

значением

косвенных

измерений

известной

зависимостью

Z =

j(X),

....

X,/"J.

Используя

правило

равноточ

ных

измерений,

все

составляющие

погрешностей

прямых

измерений

абсо

лютной

относительной

формах

примерно

должны

быть

одинаковы

по

разме

ру,

что

учетом

коэффициентов

влияния

Ь;

.С}

предъявляет

требования

вы

боруdi

ид}.

Рассмотрим

пример

расчета

погрешностей

косвенных

измерений.

для

точного

измерения

сопротивления

обычно

используют

метод

их

расчета

по

закону

Ома:

Т'

(2.9)

где

И-ток

напряжение

соответственно

Кроме

того,

так как

точны.е

амперметры

лабораториях

отсутствуют,

потенциометры

обладают

достаточно

хорошими

метрологическими

характе

ристиками,

то

значения

токов

предпочтительно

измеряют

помощью

потен

циометра,

определяя

падение

напряжения

на

образцовых

сопротивлениях

o6p

включенных

последовательно

искомым

размером

сопротивления

Rx.

Тогда

значение

тока

вычисляют,

зная

падение

напряжения

на

об

разцовом

сопротивлении

o6p

Задан

не

Найти

систематическую

случайную

составляющие

погрешности

кос

венного

результата

измерения

силы

по

зависимости

F =

а,

где

масса

тела,

ускорение.

Дано:

те

= ±0,1 %,

= ±

,05 %,

дас

±0,2%,

::::

±0,07

Задание

Найти

систематическую

случайную

составляющие

погрешности

кос

венного

результата

измерения

излучательности

по

зависимости

::::

а-

где

постоянная

Сгефана-Больцмана

(5,67.10-8

Вт/м

-к

)

Т

абсолютная

температура.

-3

-4

Дано:

00 =±10

оmн.ед"ОТе::::

±IO

оmн.ед.,От::::

±lо-5

Задание

Найти

систематическую

случайную

составляющие

погрешности

кос

венного

результата

измерения

энергии

магнитного

поля

соленоида

по

зави

В·Н

симости

-2-

.,S

'/,

где

магнитная

индукция,

коэрицитивная

си-

nа,

S-

площадь

соленоида,

длина

соленоида.

Дано:

/е

= ±

,5%,

I = ±

±0,3%,

R =

±0,05

Задание

Найти

систематическую

случайную

составляющие

погрешности

кос

венного

результата

измерения

объемного

расхода

вещества

измеряемого

расходомером

переменного

перепада

давления,

по.

зависимости

3 2

Р=4·10

-а

т-Т)

"VP'

где

коэффициент

расхода,

Е-

коэффици-

ент

сжатия

вещества,

модуль

сужающего

устройства,

D -

диаметр

тру

бопровода,

t1P -

перепад

давления

на

сужающем

устройстве,

плотность

вещества.

Дано:

постоянные

величины;

О&е

±0,7%,

±0,5%,

Dc = ±0,1 %,

D =

±0,2%,

±0,5%,

11f' =

±0,4%,

±0,8%,

::::

±0,3%.

«,

,4%,

0,2

Содержание

отчета

Не

= ±

0,6

'= ±

,5 %,

Se = ±0,1 %,

S = ±

0,05

д/е

= ±

0,05

О/

::::

±0,02

Задание

Найти

систематическую

случайную

составляющие

ПОгрешности

кос

венного

результата

измерения

мощности

тока

по

зависимости

= 12 . R,

где

1- 1'01<, R -

активное

сопротивление.

, )

Изложение

задания

по

расчету

погрешности

косвенного

результата

измерения

искомой

величины.

Формулы

для

расчета

систематической

случайной

составляющих

погрешности

косвенного

результата

измерения

искомой

величины.

З.

Расчет

количественного

значения

составляющих

погрешности

кос-

венного

результата

измерения

искомой

вел~~~.

Контрольные

вопросы:

Дать

определение

косвенного

измерения

величин.

Как

определяются

погрешности

косвенного

измерения

величин

при

линейных

зависимостях

искомой

величины

от

непосредственно

из

меряемых?

Как

определяются

погрешности

косвенного

измерения

величин

при

степенной

зависимости

искомой

величины

от

результатов

прямых

измерений

[4]?

Занятие

Х!!

Поверка

средств

измерений

Цель

занятия:

научиться

осуществлять

поверку

средств

измерений

[1, 2, 3].

Краткие

теоретические

сведения

Поскольку

функциональная

зависимость

между

выходной

величиной

(сигналом)

СИ

входными

(измеряемыми)

величинами

(см.

занятие

со

вре

менем

может

изменяться,

что

сказывается

на

увеличении

погрешности

СИ,

практической

метрологии

предусматривается

операция

поверки.

Поверка

установление,

органом

государственной

метрологической

службы

пригодности

СИ

применению

на

основании

экспериментальных

ис

следований

его

погрешности

сравнение

ее

размеров

установленными

(нор

мированными)

погрешностями

для

этого

СИ

целью

установления

его

при

годности

дальнейшей

эксплуатации

[5J.

Методические

указания

при

мер

поверки

термометра

электрического

сопротивлеиия

Рассмотрим

пример

поверки

термометра

электрического

сопротивления

(ТЭС),

который

под

воздействием

температуры

изменяет

на

выходе

значение

активного

сопротивления

Rтэс

Омах.

таблице

3.1

приведены

результаты

экспериментальных

данных

изме-

рения

сопротивления

ТЭС

при

температуре:

ОС,

ос

100

ОС.

Таблица

3.1

Данные

поверки

ТЭС

Номер.

Значение

!J.

э к

CТ

"'100

э к

CГ

J I

опыта

Ом

ос

102,13

100

+2,13

111,50

109,8

+1,70

+1,55

100

144,73

142,6

+2,13

+1,49

Измерение

сопротивления

эс

осуществлял

ось

по правилам

определения

результатов

косвенных

измерений

соответствии

правилами,

изложенными

занятии

погрешностью:

де

тэ

де

0,01

%-0,07

%<Б

<0,01 %+0,07 %.

( -

{.)('.

\,..0 \.