Богуславский Э.И. Управление качеством руды

Подождите немного. Документ загружается.

случайных величин, входящих в выборку, именуют ее элементами, а

количество этих элементов – объемом выборки.

Статистический закон распределения вероятностей

случайной величины, или распределение, – это зависимость между

возможными значениями x

случайной величины X и вероятностями

их появления Р(x

). Распределение дискретной случайной величины

Х можно представить как ряд распределения. Например, для данных

о количестве отбираемых проб можно получить возможные

значения дискретной случайной величины x

и соответствующие им

частоты m

, частости p

(или вероятности), т.е. следующее

распределение за период 100 суток:

Количество отбираемых проб x

15 16 17 18 19 20 21

Число суток с таким количеством

проб (частота m

)

12 15 28 19 10 7 9

Частость, или вероятность p

0,12 0,15 0,28 0,19 0,1 0,07 0,09

Возьмем другой пример (табл.3.1). Содержание никеля

в6руде при 20 пробах изменялось в пределах 0,08-0,566%. Размах

колебаний 6=6x

max

– x

min

, для нашего примера 6=6

Ni min

6–6

Ni max

=60,566–60,086=60,486%. Распределим эту информацию, например, на

шесть групп: в привязке к размаху /66=

08,0

или к диапазону

самих значений x

max

/6660,1, а затем и определим число проб в

каждой группе, т.е. частоту (табл.3.2).

Частота – это число появления событий в серии (группе)

наблюдений, экспериментов или распределение числовых значений

случайной величины по группам (классам), на которые разбит весь

ее диапазон от x

min

до x

max

Таблица 3.2

Распределение содержания никеля в руде,%

Класс,6% Содержание,6%

Число проб

(частота)

Частость,6%

Накопленная частость

(кумулята),6%

<60,1 0,08 2 10 10

0,09

0,1-0,2 0,13 2 10 20

0,19

Окончание табл.3.2

Класс,6% Содержание,6%

Число проб

(частота)

Частость,6%

Накопленная частость

(кумулята),6%

0,2-0,3 0,23 3 15 35

0,25

0,27

0,3-0,4 0,32 6 30 65

0,35

0,36

0,37

0,38

0,39

0,4-0,5 0,41 4 20 85

0,43

0,48

0,49

0,5-0,6 0,52 3 15 100

0,54

0,56

Сумма 20 20 100 –

Частость – это отношение частоты m, к общему количеству

событий в выборке n:

m/n.

Накопленная частость – это сумма частостей предыдущих и

рассматриваемой серии (групп). Согласно теореме Бернулли, при

неограниченном увеличении количества событий n, частость их p

бесконечно мало отличается от их вероятности.

Наглядно распределение случайных величин можно

представить в виде графиков:

6для дискретных случайных величин – многоугольника

распределений;

6для непрерывных случайных величин – гистограммы,

функции плотности вероятностей и кумуляты.

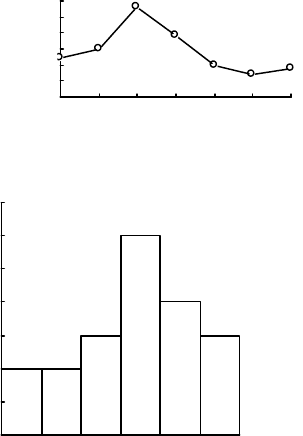
Многоугольник распределения – это график распределения

дискретной случайной величины в прямоугольной системе

координат, где x

– возможные значения X, а p6– соответствующие им

вероятности (частости). Распределение количества отбираемых в

течение суток проб графически представлено на рис.3.1.

Гистограмма – это график закона распределения случайной

величины, устанавливающего связь между возможными ее

значениями и

соответствующими им

вероятностями, в

основном, при

большом числе

исходных данных n. Их

предварительно

группируют, разбивая

весь диапазон на

равные интервалы

(классы) и

подсчитывают

количество данных,

попавших в каждый

класс, – частоту и

частость. По оси

< 0,1 0,1-0,2 0,2-0,3 0,3-0,4 0,4-0,5 0,5-0,6

Содержание никеля в руде, %

Частость (вероятность), %

Рис.3.2. Гистограмма распределения содержания

никеля в руде

0,05

0,1

0,15

0,2

0,25

0,3

15 16 17 18 19 20 21

Количество отбираемых проб в су тки

Частость (вероятность) р

Рис.3.1 Многоугольник распределения

дискретной случайной величины

абсцисс откладывают классы, а по оси ординат – частоту или

частость в виде ступенек. Гистограмма очень наглядно

характеризует случайную величину: размах и частоту конкретных

значений, степень асимметричности, равномерности и др. Для

данных табл.3.2 этот эмпирический поинтервальный график

представлен на рис.3.2.

Функция плотности вероятности непрерывной случайной

величины, или плотность распределения f(x) представлена гладкой

кривой, характеризующей результаты наблюдений или

экспериментов и вероятность попадания выборочного значения

случайной величины x

в заданный интервал от х до х6+6x. По оси

ординат откладывают частости, соответствующие каждой группе

(классу) значений случайной величины (рис.3.3).

Функция распределения вероятностей (кумулята) F(x)

определяет вероятность того, что выборочное значение случайной

величины x

окажется меньше предела, заданного переменной х, т.е.

вероятность события x

66х. При построении графика кумуляты по

оси ординат откладывают накопленные частости. Кумулята (рис.3.4)

данных (табл.3.2) позволяет определить, что, например, при

минимально допустимом содержании никеля в руде, равном 0,26%,

до 286% запасов месторождения будут забалансовыми, а при

содержании 0,356% – до 656%.

0,05

0,05 0,15 0,25 0,35 45 0,55

Содержание никеля

, %

Плотность вероятностей

(

Рис.3.3 График функции плотности

вероятностей (плотности

распределения) – дифференциальная

функция распределения

Плотность вероятностей f(x), %

Содержание никеля Х, %

Содержание никеля в руде Х, %

Накопленные частости F(x), %

Рис.3.4 График функции распределения

вероятности (интегральная функция) –

кумулята

3.2.=Числовые характеристики

распределения

случайных величин

Полную, исчерпывающую характеристику случайной

величины дают законы распределения. Для решения оперативных,

плановых и прогнозных задач управления качеством руды зачастую

нет необходимости полностью описывать случайную величину,

исследуя функции f(x) или F(x). Достаточно знать только

существенные особенности случайной величины, именуемые

числовыми или статистическими характеристиками.

Указанные характеристики могут быть двух родов:

теоретическими и эмпирическими. Теоретические иногда называют

параметрами распределения случайных величин, а эмпирические –

выборочными (статистическими) оценками этих параметров.

Параметры распределения обычно представлены

детерминированными величинами, а выборочные оценки –

стохастическими (случайными) величинами.

К наиболее распространенным числовым (статистическим)

характеристикам относятся медиана, мода, среднее значение,

дисперсия, среднеквадратическое отклонение, коэффициент

вариации, математическое ожидание, асимметрия и эксцесс.

Медиана – это центр (средний член) упорядоченного ряда

значений случайной величины Х; она делит площадь под кривой

плотности распределения пополам. Медиану можно определить,

расположив все значения x

по возрастанию (убыванию) и отыскав

средний по порядку член ряда. При четном числе рядов медиана

определяется как полусумма двух средних рядов.

Мода – это значение x

, которому соответствует наибольшая

вероятность (частота или частость).

Среднее значение случайной величины – это

среднеарифметическое из всех ее значений:

6=6





Дисперсия – это мера рассеивания (отклонения) случайной

величины относительно центра ее группирования. Она является

главной характеристикой разброса случайной величины и

вычисляется как усредненный квадрат отклонения случайных

значений величины от ее среднего значения

D6=6



















Среднеквадратическое (стандартное) отклонение

6=6

6=6



















Для вычисления выборочного среднеквадратического отклонения

при n6<6(2030), в знаменателе п заменяется п–1. Это значение 

зачастую именуется исправленным.

Коэффициент вариации случайной величины

(эмпирический) – это отношение среднеквадратического отклонения

к среднеарифметическому значению (в долях единицы или в

процентах):

6=6

x/

. (3.1)

Эта характеристика случайной величины служит критерием

корректности наблюдения или эксперимента. Можно считать, что

технические измерения достаточно достоверны при 6<656%,

геологические и горные исходные данные и эксперименты при

6<610156%. Кроме того, коэффициент вариации широко

используется для характеристики степени изменчивости изучаемых

свойств, параметров и показателей геологических, горных и

обогатительных объектов и процессов, имеющих, как правило,

различные размерности.

Математическое ожидание выражается для дискретной

случайной величины через сумму произведений всех ее возможных

значений x

на соответствующие им вероятности p

М(х)6=6





Для непрерывной случайной величины математическое ожидание

М(х)6=6







dxxxf )(

Этот параметр равен абсциссе центра тяжести функции плотности

вероятностей f(х) и характеризует ожидаемое среднее значение

случайной величины. Он широко используется для оценок в горно-

геологической и обогатительной практике, в частности для

определения среднего содержания полезных компонентов, при

подсчете запасов месторождения или его участков, планировании

горных работ, при оценке прочностных свойств горных пород,

гранулометрического, химического и минерального состава руды и

др.

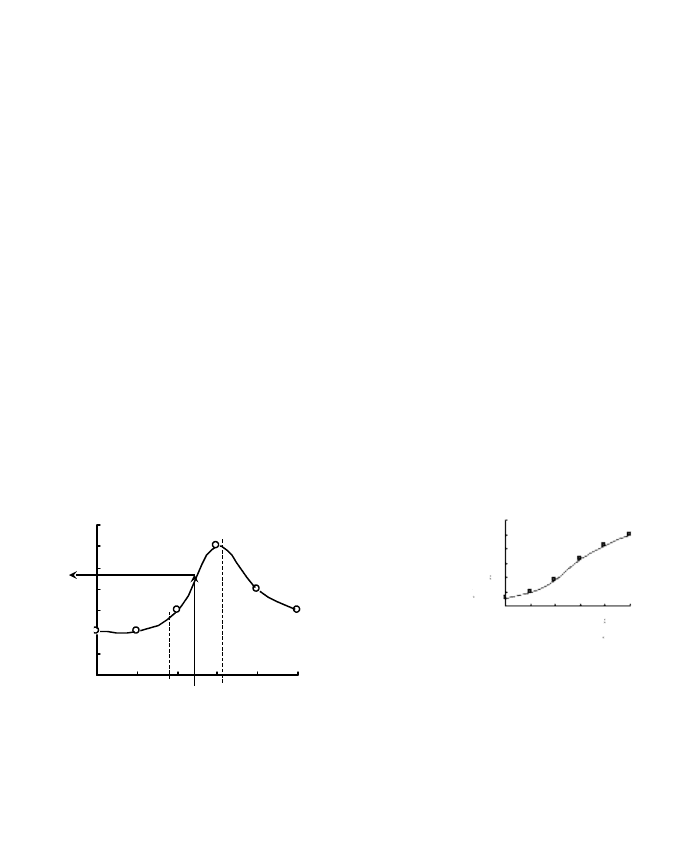
Асимметрия – это смещение пика графика плотности

распределения (математического ожидания) от центра размаха

варьирования (рис.3.5). Для дискретной случайной величины она

определяется через кубы отклонений либо через частости

соответственно

nxxA

/)(













pxMxA

)]([

а для непрерывной – через плотность распределения и

математическое ожидание:







 dxxfxMxA )()]([

. Для

симметричных распределений асимметрия равна нулю. Если мода,

медиана и математическое ожидание смещены относительно центра

размаха варьирования влево, то А6>60 и распределение

положительно асимметричное (рис.3.5, кривая61), а6если вправо, то

A6<60 и6оно отрицательно асимметричное (рис.3.5, кривая63).

Эксцесс – это числовая характеристика кривой плотности

вероятностей, отражающая степень ее «крутости» или

островершинности (рис.3.6). Островершинные распределения

характеризуют приуроченность подавляющего большинства

значений случайной величины к узкой области, примыкающей к

Рис.3.6. Графики функции плотности

распределения с различным эксцессом

1, 2 и 3 – показатель эксцесса соответственно

положителен, равен нулю и отрицателен

f(х)

Рис.3.5. Графики функции плотности

распределения с разной асимметрией

1 и 3 – положительно и отрицательно

асимметричное соответственно;

2 – симметричное

f(x)

моде, плосковершинные – рассеянность ее по всему интервалу

возможных значений. Мерой эксцесса служит четвертая степень

отклонений:

Е6=6

nxx

/)(







; Е6=6







pxMx

)]([

;

Е6=6







 dxxfxMx )()]([

Показатели асимметрии A

6=6А/

и эксцесса Е

6=6Е/

служат

для оценки соответствия выборочных данных конкретному типу

распределения.

Эксцесс нормального распределения обычно

рассматривается как эталон. Так как Е

6=63, для сопоставления

различных распределений его принято представлять в виде

6=6Е/

–3.

При оценках непрерывной случайной величины по

сгруппированным выборочным данным вероятности р

заменяются

частотами попадания значений х

в каждый интервал группирования

, а значения х

– значениями центров интервалов группирований x

Тогда формулы для определения математического ожидания М(х'),

среднеквадратического отклонения ', показателей асимметрии А

' и

эксцесса Е

' принимают следующий вид:

М(х')6=6





; '6=6



















;

'6=6

)(









; Е

'6=6

)(









Момент случайной величины удобен для определения

статистических характеристик случайной величины и вычисляется

как сумма отклонений случайной величины x

от относительно

постоянной q в различных степенях k (от 1 до 4):







.)(

Параметр q может быть выбран произвольно, равным нулю

или среднему значению

. В первом случае момент случайной

величины именуется произвольным (им пользуются для ускорения

вычислений). Во втором случае момент именуется начальным и

среднеарифметическое его значение

определяется через момент

первого порядка:

6=6m

. Начальный момент

6=6





(3.2)

В третьем случае момент называется центральным:







.)(

(3.3)

Статистические характеристики (дисперсия D,

среднеквадратичное отклонение , показатели асимметрии А

эксцесса Е

) легко вычисляются через центральные моменты

случайной величины:

D6=6

; 6=



; А

6=6

/

; Е

6=6

/

–3. (3.4)

Весомые преимущества использования моментов случайной

величины для вычисления статистических характеристик дает

применение персональных компьютеров, особенно пакетов

электронных таблиц Excel для среды Windows. Пример такого

расчета для оценки численных характеристик распределения

содержания железа в руде показан в табл.3.3.

По данным табл.3.3 и формулам (3.1)-(3.4) легко определить

следующие параметры ряда:

6=644,44; D6=659,36; 6=

= =

36,59

6=67,7; 6=6/

6=67,7/44,446=60,173; A6=6–218,12; А

6= =6А/



6=6–218,12/456,536=6–0,41; Е6=68740,94; Е

6=6Е/

–36=

=68740,94/3515,3–36=6–0,51. Таким образом, эта серия проб

содержания железа в руде характеризуется следующими

показателями: медианой 456%, среднеарифметическим значением

случайной величины 44,446%, средним квадратическим отклонением