Боевкин В.И., Окин А.А., Шныров А.Б. Моделирование процессов в электрических сетях
Подождите немного. Документ загружается.


МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 2003г., том 15, номер 2, стр. 3-13
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ СЕТЯХ
© В.И.Боевкин, АА.Окин, А.Б.Шныров
Рассмотрены различные варианты оптимизации итерационных решений систем линейных алгеб-
раических уравнений, применяемых при математическом моделировании режимов электрических
сетей. В качестве параметра оптимизации использован комплексный множитель. Исследована
сходимость различных итерационных методов решения в зависимости от варианта оптимизации.
Показана зависимость числа итераций от варианта оптимизации. Исследование было проведено с
использованием оценки сходимости по корням характеристического уравнения. В работе исполь-
зованы данные, полученные в результате расчетов электрических сетей различных конфигураций.
MODELLING OF THE PROCESSES
IN THE ELECTRICAL POWER NETWORKS
V.I.Boevkin,
A.A.Okin,
A.B.Shnyrov
The various variants of optimization of the iterative solutions of systems of the linear algebraic equa-
tions used at mathematical modeling of modes of electrical networks are considered. The complex
multiplier is used as parameter of optimization. The dependence of convergence of various iterative
methods of the solution on variant of optimization is investigated. The dependence of number of itera-
tions on variant of optimization is shown. The research was carried out with use of an estimation of
convergence on roots of the characteristic equation. In work the data are used received as a result of
calculations of electrical networks with different configurations.
Введение
При математическом моделировании процессов в электрических сетях, в частности, при
решении уравнений установившегося режима (УУР), на промежуточных этапах вычислений
часто приходится решать линейные алгебраические системы уравнений. Параметры решаемой
системы могут быть как вещественными (сети постоянного тока), так и комплексными (сети
переменного тока).
При решении УУР характерными особенностями матрицы являются большая размер-
ность, порядка 10000, диагональное преобладание и разреженность (слабая заполненность) [1].
При слабой заполненности матрицы во многих случаях предпочтительнее пользоваться итера-
ционными методами решения, в которых одним из важнейших факторов является скорость
сходимости [2]. В настоящей работе для достаточно общей методики формирования итераци-
онных схем решения даны варианты оптимизации скорости сходимости по комплексному
множителю.
Оценка сходимости по корням характеристического уравнения
Рассмотрим решение системы линейных уравнений
AX=F,
(1)

4
В.И.Боевкин,
А.А.Окин,
А.Б.Шныров
где матрица А является симметричной, диагонально-доминантной, разреженной, а ее коэффи-
циенты - комплексные числа.
Общая методика построения стационарных итерационных схем решения линейной сис-
темы уравнений (1) может быть представлена, согласно [6], [7], [8], в виде
D[X(k +1) - X(k)] = C[F-A- X(k)}. (2)
Здесь D - произвольная неособая матрица, С - произвольный матричный, или скалярный
(комплексный) множитель. Из способа построения разностного уравнения (2) видно, что его
установившееся решение совпадает с решением уравнения (1) при любых С и D, обеспечи-
вающих сходимость итерационного решения. Для оценки скорости сходимости итераций при-
меним к разностному уравнению (2) операцию Z-преобразования [3], то есть приведем его к
операторной форме:
[z-D-(D-CA)]X(z)
=
CF(z). (3)
Характеристическое уравнение системы (3) имеет вид
det[z-D-(D-C ,4)] = det(D)det{/z-[/-D-
1
C-^]} = 0. (4)
Корни
ZuZb..>*Zn (5)
характеристического уравнения (4) являются собственными значениями матрицы £, именуемой
в [8] оператором шага:
E = [I-D-
l
-C-A]. (6)
Общее решение разностного уравнения (3) при F=const для случая некратных корней можно
записать
X(k) = S
0
+ S
r
z!+S
2
.z
k
2
+... +
S
n
.'Z
k
n
.
(7)
Если модули всех корней (5) меньше единицы, то решение (7) при &-»оо сходится к устано-
вившемуся значению So, совпадающему с решением уравнения (1). Скорость сходимости мож-
но оценить по наибольшему по модулю корню
z
jmax
.
Задавшись допустимой относительной ошибкой е, оценим число итераций г:
( \
е
log]
г>
lOgkmax
(8)
Оптимизация сходимости по скалярному множителю
При скалярном С из (6) можно получить:
£ = [/-С#], H
=
D~
]
A. (9)
При выбранной тем или иным способом матрице D, то есть выбранном методе итера-
ционного решения, матрица Н из (9) становится известной, и ее собственные значения опре-
деляются уравнением

Моделирование процессов
в
электрических сетях
5
det[/
y-H] = 0. (10)
Сходимость итерационного решения определяется собственными значениями матрицы
£, то есть корнями уравнения
det[/z-£] = det[/z-(/-C^)] = (-C)det[/. — -#] = 0. (11)
Уравнения (10) и (11) совпадают с точностью до обозначений
У-^JT'
z = l-C-y, (12)
поэтому собственные значения матриц Е и Н связаны этими же соотношениями:
>>,= —
>
Zj=\±C.y
p
j =
\,-
t
n.
(13)
Сходимость итерационного процесса определяется величиной
z
max
=max|l-C-.v
y
|,
У
=
1,-,л.
Поскольку множитель С произволен, то по нему возможна минимизация количества итераций.
В упомянутых выше работах производится аналитическая оптимизация по множителю С
в предположении вещественности корней уравнения (10) и самого оптимизирующего множи-
теля.
Это накладывает на матрицу Н ограничения, которые не всегда выполняются для матриц
электросетей. В этих случаях рекомендуется оптимизирующий параметр находить подбором
[2],
[5].
Рассмотрим задачу в несколько более общей постановке, для комплексных Л и С. Пусть
собственные значения yj матрицы Н произвольно расположены в ограниченной области ком-
плексной плоскости у и заданы своими модулями Rj и аргументами а/.
y
j
=R
J
'e
ia
\
у = 1,»-,я. (14)
При произвольном комплексном С, заданном модулем X и аргументом Ь
ь
после преоб-
разования (13) соответствующие корни z/ характеристического уравнения (собственные значе-
ния матрицы Е) будут:
C =
X-e
ib
;
zj =\-R
j
-X'[cos(a
j
+b) + ism(a
J
+b)]
i
у = 1,-•-,/!. (15)
Задача оптимизации сводится к нахождению таких X и
Ъ
у
которые обеспечивают распо-
ложение всех
Zj
из (15) внутри окружности минимального радиуса с центром в начале коорди-
нат комплексной плоскости. Иначе говоря, нужно минимизировать наибольший по модулю г
}
.
Сформируем кусочно-непрерывную функцию двух переменных:
t/(^,6)=l|z,|
2
.n(|z,|
2
>|z.|
2
). (16)
j*k
Здесь использована логическая функция
(КГ
>
кГ)
= 1 П
Р
И
Ы
2>
К|
2;
иначе (|z,|
2
>|z
;
|
2
) = 0.
Численная минимизация (16) решает поставленную задачу, однако требует весьма большого
объема вычислений, поскольку на каждом шаге оптимизации необходимо вычислять и ранжи-
6
В.И.Боевкин,
АЛ.Окин,
А.Б.Шныров
ровать все \z
k
\ . Кроме того, необходимо убедиться в том, что оптимизированное значение
U(X,b)
min
из (16) меньше единицы.
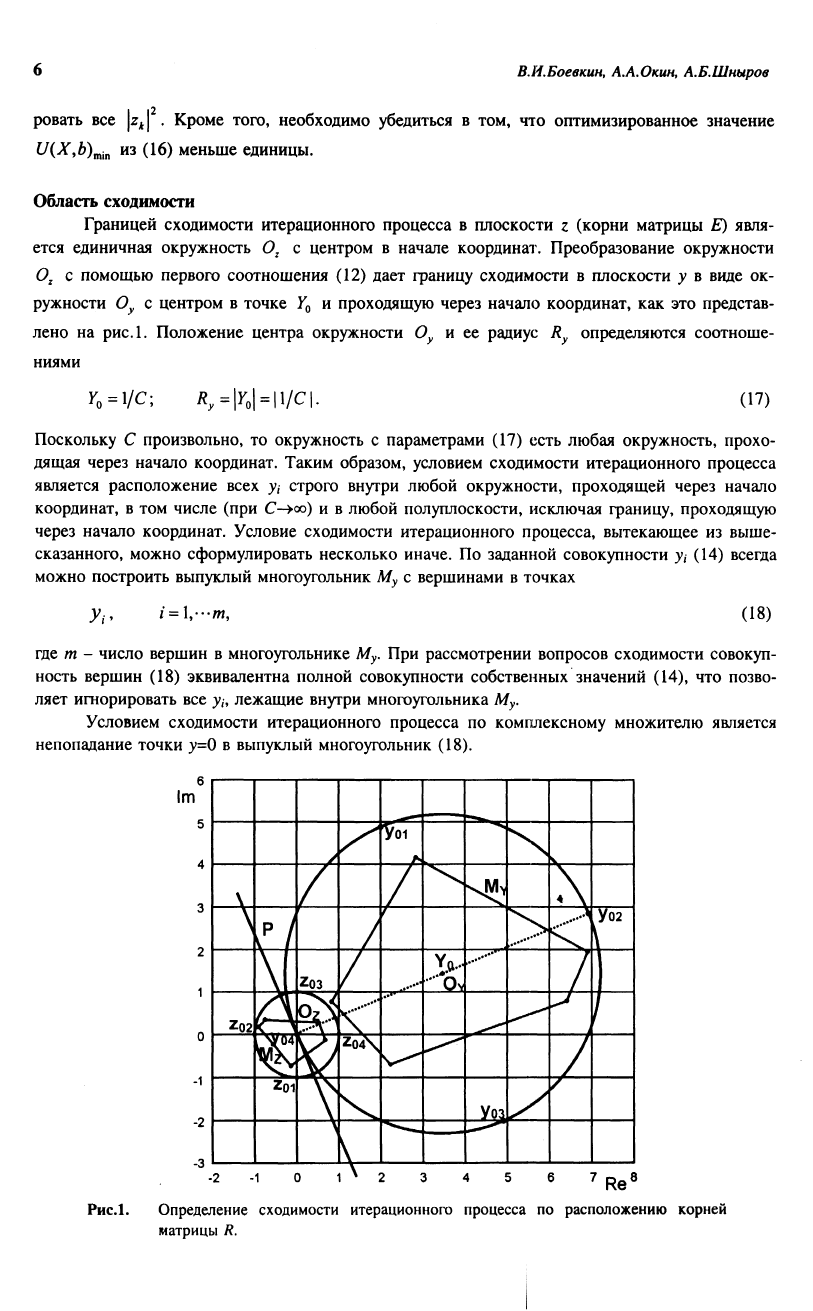
Область сходимости
Границей сходимости итерационного процесса в плоскости z (корни матрицы Е) явля-
ется единичная окружность О
г
с центром в начале координат. Преобразование окружности
O
z
с помощью первого соотношения (12) дает границу сходимости в плоскости у в виде ок-
ружности О
у
с центром в точке У
0
и проходящую через начало координат, как это представ-
лено на
рис.1.
Положение центра окружности О
у
и ее радиус R определяются соотноше-
ниями
У
0
= 1/С; Л,=|У
0
| = |1/С|. (17)
Поскольку С произвольно, то окружность с параметрами (17) есть любая окружность, прохо-
дящая через начало координат. Таким образом, условием сходимости итерационного процесса
является расположение всех у, строго внутри любой окружности, проходящей через начало
координат, в том числе (при С-><») и в любой полуплоскости, исключая границу, проходящую
через начало координат. Условие сходимости итерационного процесса, вытекающее из выше-
сказанного, можно сформулировать несколько иначе. По заданной совокупности у, (14) всегда
можно построить выпуклый многоугольник My с вершинами в точках
У
п
i = l,-«, (18)
где т - число вершин в многоугольнике М
у
. При рассмотрении вопросов сходимости совокуп-
ность вершин (18) эквивалентна полной совокупности собственных значений (14), что позво-
ляет игнорировать все у,, лежащие внутри многоугольника М
у
.
Условием сходимости итерационного процесса по комплексному множителю является
непопадание точки у=0 в выпуклый многоугольник (18).
Рис.1.
Определение сходимости итерационного процесса по расположению корней
матрицы R.

Моделирование процессов
в
электрических
сетях
1
Рис Л иллюстрирует упомянутые выше объекты: единичную окружность О
г
с
обозначен-
ными точками z
m
...z
m
, окружность
О
у
с
параметрами (17)
и
соответствующими точками
Уо\
— Ум>
границу полуплоскости Р, образованную из
О
у
при |^
0
| = оо, выпуклый многоуголь-
ник
М
у
в
плоскости
у с
параметрами (18), выпуклый многоугольник
М
2
в
плоскости z, пре-
образованный из
М
у
вторым соотношением (12).
Оптимизация по двум точкам
Пусть заданы два собственных значения у\ и уг матрицы Я, формирующие отрезок
L
yt
а также произвольный комплексный множитель С:
y
x
=R
x
-e
ia
\ y
2
=R
2
-e
ia
\
C
=
X-e
ib
.
(19)
Соответствующие корни
ZI*H
ZI характеристического уравнения (4), исходя из (13), будут:
z, =1-Д, •А'-совЦ +
Ь)
-
i
•
R
x
•
X
•
sin(a, + b),
z
2
=
1
-
R
2
X
•
cos(a
2
+ b)
-
i
•
R
2
•
X
•
sin(a
2
+ b).
(20)
Задача оптимизации заключается
в
выборе параметров X
и b
из условия минимизации наи-
большего из модулей |z,
|,
|z
2
1. Выражения U\z для квадратов модулей получим из (20):
U
x
=\z
x
\
2
=X
2
-R
x
2
+
\-2
X-R
x
-cos(a
x
+b\
t/
2
=|z
2
|
2
=A
r2
.
J
R
2
2
+ l-2-A
r
./?
2
-cos(a
2
+6).
(21)
При фиксированном (Ь) зависимости (21) являются квадратными параболами от X, проходя-
щими через точку Х=0, £Л,2=1.
Условием оптимизации является равноудаленность двух точек от начала координат, что
обеспечивается при пересечении кривых (21):
U
x
=U
2
=X
2
R
x
2
+
\-2-X-R
x
-cos(a
x
+b)
=
X
2
-R^+
1-2-X'R
2
-cos(a
2
+b).
Отсюда
X•
(R
x
2
-R
2
2
)
=
2[R
X
-cos(a, +b)-R
2
-cos(a
2
+ b)].
(22)
Особенным является случай равных модулей #i=/?2, для которого, из (22):
cos(tf,
+ b) = cos(a
2
+ b), (a, +
b) =
-(a
2
+ b), b
=
-(a
x
+a
2
)/2
.
Кривые (21) при этом совпадают.
В общем случае координату Х
р
точки пересечения получим из (21):
X
p
=2-[R
r
cos(tf, +b)-R
2
cos(a
2
+ b)]/(R
2
-R
2
). (23)
Значение U=Ui(X
p
) в точке пересечения является функцией от Ь:
U(b) =
X
2
p
-Rf+l-2-X
p
R,
-cos(fl, +fe). (24)
Минимизация (24) по
&
решает задачу оптимизации по комплексному множителю для отрезка
L
y
.
Приравняем нулю производную dU/db , откуда:
dX
p
Idb
•
[R
x
•
Х
р
-
cos(a, +
b)]
+ X
p
•
sin(a, + b)
=
0 .
(25)

8
В.И.Боевкин,
А.А.Окин,
А.Б.Шныров
Из (23):
dX
p
ldb =
2
l(R
2
- R
2
)
•
[R
2
•
cos(tf
2
+b)-R
x
sin(a, +Ь)]. (26)
Подставив (26) в (25) и проделав необходимые выкладки с использованием известных триго-
нометрических соотношений, можно получить выражение для оптимального значения
Ъ
т
:
tg(2 -b
m
)
=
-tg(e, + а
2
), b
m
= -(а, + а
2
) /
2.
(27)
Подставив (27) в (23) и (24), получим выражения для оптимальных значений всех параметров:
Ь
т
= -(*, + а
2
)/2, ^
=2.COS[(A
2
-a
x
)l2]l(R
x
+ Л
2
),
U
m
=L
2
/(R
x
+R
2
)\ L
2
=R
2
-2R
x
-R
2
cos(a
2
-a
x
) + R
2
y
(28)
R
z
=Rad{UJ = L/(R
x
+R
2
).
Здесь L - длина отрезка Ly\ R
z
- радиус окружности O
z
в плоскости z с центром в точке z=0,
на которой лежат корни ц и zi, определяющие скорость сходимости итерационного процесса
(радиус сходимости).
Из (19) и (28) получим выражение для оптимального множителя С
т
\
С
т
= Х
рт
•
e
ib
"
=
2• {cos[(a
2
-а
х
)/2]•
<?-'<**"
)/2
}/(Л, + Д
2
). (29)
Преобразование (12) y
=
(\-z)IC
при C = C
m
переводит окружность О
г
в окружность О
у
,с
центром в точке
У
0
=
1
/ С
т
и проходящую через точки у
х
и у
2
. Положение центра У
0
и ра-
диус R
y
окружности О
у
получим из (28) и (29):
Y
0
= l/C
m
=e-
ib
»/X
pm
=[(R
x
+R
2
).e
iia
^
)>2
y
\Y
0
\=\/X
pm
=(R
]
+R
2
)/{2.cos[(a
2
-a
]
)/2]}, (30)
R
y
=\y
]
-Y
0
\=\y
2
-Y
0
\=R
2
/X
pm
=L/2^os[(a
2
-a
x
)/2].
При а
х
=
а
2
, когда у
х
и у
2
располагаются на одном луче, из (28) можно получить
Х
рт
=2/(Л,+/г
2
), R,=(R
l
-R
i
)/(R
i
+B
i
), (31)
что совпадает с соответствующими выражениями для вещественных корней [2].
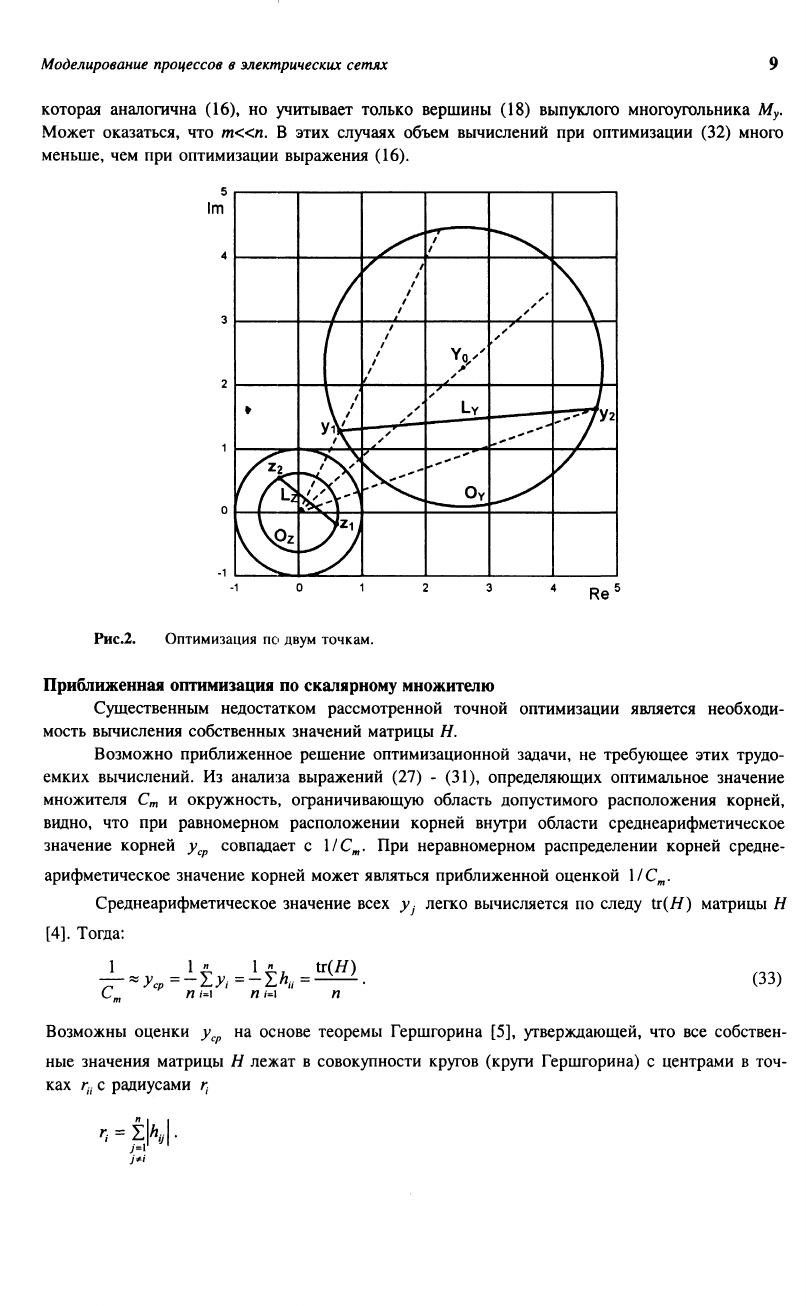
На рис.2 представлена комплексная плоскость и все объекты, обсуждаемые выше.
Отрезок L
y
с собственными значениями у\ и уг на концах, лучи, проходящие через у\ и
Уг
и биссектриса между ними, оптимальная окружность О
у
с центром в точке Ко» расположен-
ном на указанной биссектрисе, и радиусом R
y
, оптимальная окружность O
z
в плоскости z с ра-
диусом R
z
и отрезком L
z
со значениями z\ и zi на концах. Если все остальные собственные
значения матрицы Н расположены внутри окружности О
уу
то найденные выше значения (28)-
(33) являются строго оптимальными для всей совокупности y
i
.
В качестве отрезка Ly целесообразно выбрать наибольшую хорду многоугольника М
у
.
Если многоугольник М
у
не располагается внутри окружности О
уу
то выбор множителя С мож-
но произвести путем численной минимизации кусочно-непрерывной функции
U(XM =
p
k
\-m\z
k
\
2
>\zj\
2
),
(32)
fa
Моделирование процессов
в
электрических сетях
9
которая аналогична (16), но учитывает только вершины (18) выпуклого многоугольника М
у
.
Может оказаться, что т«п. В этих случаях объем вычислений при оптимизации (32) много
меньше, чем при оптимизации выражения (16).
Рис.2.
Оптимизация по двум точкам.
Приближенная оптимизация по скалярному множителю
Существенным недостатком рассмотренной точной оптимизации является необходи-
мость вычисления собственных значений матрицы Н.
Возможно приближенное решение оптимизационной задачи, не требующее этих трудо-
емких вычислений. Из анализа выражений (27) - (31), определяющих оптимальное значение
множителя С
т
и окружность, ограничивающую область допустимого расположения корней,
видно, что при равномерном расположении корней внутри области среднеарифметическое
значение корней у
ср
совпадает с 1/С
т
. При неравномерном распределении корней средне-
арифметическое значение корней может являться приближенной оценкой 1/С
ш
.
Среднеарифметическое значение всех у
i
легко вычисляется по следу tr(#) матрицы Н
[4].
Тогда:
1 1- 1- 1г(Я)
— *
Уср
= -5>, =-ХЛ„ = • (33)
С
т
п
/=i
n
/=1
п
Возможны оценки у
ср
на основе теоремы Гершгорина [5], утверждающей, что все собствен-
ные значения матрицы Н лежат в совокупности кругов (круги Гершгорина) с центрами в точ-
ках г
и
с радиусами г
{
п
i i

10
В.И.Боевкин,
АА.Окин,
А.Б.Шныров
Центр окружности наименьшего радиуса, охватывающей
все
круги Гершгорина, может являть-
ся приближенной оценкой величины
у .
Возможны
и
другие приближенные оценки,
не
тре-
бующие вычисления собственных значений матрицы
Я.
Ускоряющий матричный множитель
Легко показать,
что
приближенная оценка
(33)
оптимизирующего скалярного множите-
ля
С
т
по
следу матрицы
Н
обращает
в
нуль след матрицы перехода
Е:
=
„- "
tr(#) =
0.
(34)
tr(tf)
Можно предположить,
что
обращение
в
нуль всех диагональных элементов матрицы
Е
приве-
дет
к
ускорению итерационного процесса
по
сравнению
с (33).
Такая процедура переместит центры всех кругов Гершгорина, построенных
по
матрице
£,
в
начало координат плоскости
Z.
Обнулить
все
диагональные элементы матрицы
Е
возможно путем использования
в ка-
честве оптимизирующего множителя
С в (2)
соответствующим образом определенной диаго-
нальной матрицы.
Определим элементы матрицы
С для
метода Гаусса-Зейделя. Приведем систему уравне-
ний
(1) к
виду BX=f путем умножения обеих частей матричного уравнения
(1)
слева
на
мат-
рицу
I/ , где
1А
-
диагональная матрица, построенная
из
диагональных элементов матрицы
А.
Исходное разностное уравнение
(2)
примет
вид
D'{x{k
+
\)-X{k))
=
C-(f-B-X(k)).
(35)
Если
в
качестве
D в (35)
выбрать матрицу
(/
+ £„),
где В
п
-
строго нижняя треугольная мат-
рица, образованная
из
элементов матрицы
В, и
принять
С=/, то мы
получим векторно-мат-
ричный итерационный процесс
в
неявной форме, соответствующий методу Гаусса-Зейделя
[7],
[8]:
{l
+
B.)-(x(k
+
\)-X{k)) =
f-B-X{k).
(36)
Очевидно, очередность введения
в
уравнение
(35)
неособых матриц
D и С
может быть
любой. Отсюда возможны следующие
два
варианта разностного уравнения, соответствующего
методу Гаусса-Зейделя,
с
ускоряющим матричным множителем
О/:
1-й
вариант:
(/
+
В
п
\С
-1
•
(х(к
+1)-X(k))
=
f-B-Х(к),
4
(37)
2-й вариант:
C-
l
{l
+ B
H
)-(x{k
+
\)-X(k))=
f-B-Х{к).
(38)
Из этих уравнений легко получить выражения
для
операторов шага (матрицы
Е):
1-й
вариант:
Е = / -
С
•
(/
+
В
п
)"'
•
В , (39)
2-й вариант:
£ = /-(/
+5
Л
)
-1
С В . (40)
Отметим,
что
если
в
качестве оптимизирующего множителя
С
выбрать скаляр,
то оба эти ва-
рианта сведутся
к
одному варианту оптимизации метода Гаусса-Зейделя
по
скалярному мно-
жителю
с
оператором шага:
E
=
I-CH
=
I-C(I+B„)-
1
B.
tr(£)=tr(/-ctf)
=
tr /
\т(н)
Н

Моделирование процессов в
электрических
сетях
11
Из условия равенства нулю элементов главных диагоналей матриц перехода (39) и (40)
для каждого варианта найдем выражения для определения элементов ускоряющих матричных
множителей С.
В первом варианте получим независимые выражения всех элементов матрицы С через
элементы матрицы В. Во втором варианте получим набор рекуррентных выражений элементов
матрицы С через элементы матрицы В и младшие элементы матрицы С.
Получаемые выражения для элементов матрицы С имеют вид
с
<
=
^ч,
Тл '
/ = 0
-
я
-
1
<
41
>
7=0
И
С,
= 1,
C
l
=\-'2t!
+
B.Y
,
)
J
.C
J
-B
JJ
,
; =
1.../»-1, (42)
где п - порядок системы уравнений.
Первому варианту соответствуют выражения (41), а второму - (42).
Так как матрица (l
+
B
n
) является треугольной, то элементы обратной к ней матрицы
(l
+
B
n
)~\ входящей в выражения (41) и (42), легко выражаются аналитически через элементы
исходной матрицы (/ + В
п
).
Необходимо отметить, что оптимизация по матрице, так же как и оптимизация по сле-
ду, не требует вычисления собственных значений.
Результаты расчетов
В настоящее время существуют высокоэффективные итерационные методы решения
систем линейных уравнений, но они применимы для вещественных и эрмитовых матриц [7]. В
данной работе рассматривались неэрмитовы матрицы с комплексными коэффициентами. По-
этому расчеты производились итерационным методом Гаусса-Зейделя с оптимизацией по ком-
плексному множителю.
В расчетах использовались матрицы узловых проводимостей электросетей переменного
тока 49,195 и 333-го порядков. Все использованные матрицы - симметричные, диагонально-
доминантные, разреженные, с комплексными элементами.
В расчетах определялось число итераций при значении абсолютной предельной по-
грешности [9], равной 0.05 (что соответствует допустимой относительной ошибке е = 510~
5
).
При этом рассматривались следующие случаи:
- без оптимизации по (36);
- с приближенной оптимизацией по (38) и (33);
- с точной оптимизацией по (38) и (16), (или 29);
- с использованием ускоряющего матричного множителя С по (37) и (41) - первый ва-
риант (второй вариант с ускоряющим матричным множителем, определенным по (38) и (42) дал
меньший эффект, чем первый и его результаты не приводятся).
Результаты расчетов приведены в табл. 1.
Кроме количества итераций, полученных по счету, табл. 1 содержит также их оценки,
вычисленные по формуле (8), и коэффициенты ускорения счета, полученные как отношения
числа итераций в конкретном оптимизированном варианте к числу итераций в варианте без
оптимизации.

12
В.И.Боевкин,
А.А.Окин,
А.Б.Шныров
Таблица 1
Порядок матрицы
Без оптимизации
С точной оптимизац.
Уск-ние сходимости
С оптимиз. по следу
Уск-ние сходимости
С оптимиз. по матрице
Уск-ние сходимости
10
Счет
76
58
1.3
64
1.19
60
1.27
Оценка
78
50
1.56
66
1.18
61
1.28
49
Счет
112
69
1.62
95
1.18
83
1.35
Оценка
111
69
1.61
94
1.18
81
1.37
195
Счет
250
174
1.44
210
1.19
159
1.57
Оценка
246
155
1.59
207
1.19
157
1.57
333
Счет
296
190
1.56
252
1.175
207
1.43
Оценка
304
194
1.57
259
1.7
210
1.45
Из табл. 1 для рассмотренных случаев можно видеть следующее.
1) По сравнению с неоптимизированным методом Гаусса-Зейделя:
- точная оптимизация по собственным значениям сокращает число итераций в 1,3
1,62 раза;
- приближенная оптимизация по следу сокращает число итераций в 1,18 - 1,19 раза;
- оптимизация по матрице сокращает число итераций в 1,27 - 1,57 раза и по своей эф-
фективности близка к точной оптимизации по скалярному множителю.
2) В рассмотренных примерах теоретические оценки числа итераций в целом незначи-
тельно отличаются от числа итераций, полученных в практических расчетах.
Заключение
Рассмотрены варианты оптимизации итерационных решений систем линейных алгеб-
раических уравнений по скалярному и матричному комплексному множителю. Для метода Га-
усса-Зейделя показана качественная зависимость числа итераций от варианта оптимизации.
Приближенная оптимизация по матричному оптимизирующему множителю без вычисления
собственных значений дает ускорение сходимости итерационного процесса, близкое к ускоре-
нию от точной оптимизации по скалярному множителю. Полученные результаты могут быть
использованы при итерационных решениях систем линейных алгебраических уравнений для
сетей переменного тока, описываемых матрицами с комплексными элементами.
В дальнейшем имеет смысл исследовать возможность дополнительного ускорения схо-
димости итерационных решений за счет сочетания предложенных методов с методами непол-
ной факторизации, прореживания итераций и др.
Пользуясь случаем, авторы выражают глубокую благодарность участникам семинара
проф.
Забродина А.В. за полезное обсуждение материалов статьи и ценные замечания.
СПИСОК ЛИТЕРАТУРЫ
1.
Горнштейн
В.М.
и
др.
Методы оптимизации режимов энергосистем. - М.: Энергия, 1981, 336 с.
2.
Брамеллер
А.,
Аллан Р.,
Хэмэм
Я. Слабозаполненные матрицы: Анализ электро-энергетических сис-
тем. - М: Энергия, 1979. 192 с.
3.
Кузовков
Н.Т.
и
др.
Непрерывные и дискретные системы управления и методы идентификации. - М:
Машиностроение, 1978, 222 с.
4.
Беллмон
Р.
Введение в теорию матриц. - М.: Физматгиз, 1969, 368 с. »
5.
Ортега
Дж.,
Пул
У.
Введение в численные методы решения дифференциальных уравнений. - М.:
Наука, 1986, 288 с.
