Боднарчук Ю.В., Олійник Б.В. Методичні рекомендації. Дискретна математика
Подождите немного. Документ загружается.

Роздiл 7
Теорiя графiв.
Означення 7.0.1. Загальним орiєнтованим графом називається суку-
пнiсть
G = (V, E, L, ∂
E
, ∂
L
), яка складається з трьох множин V − множина вер-
шин ( vertexes), E− множина ребер (edges),L− множина петель (loops) та
вiдображень:
∂
E
: E → V × V,
∂
L
: L → V.
При цьому якщо ∂
E
(e) = (v
1
, v
2
), то вершину v
1
будемо називати початком
ребра e, а вершину v
2
її кiнцем .
Означення 7.0.2. Загальним неорiєнтованим графом називається суку-
пнiсть
G = (V, E, L, ∂
E
, ∂
L
), яка складається з трьох множин V − множина вер-
шин ( vertexes), E− множина ребер (edges),L− множина петель (loops) та
вiдображень:
∂
E
: E → C
2
V
− множина двохелементних пiдмножин множиниV,
∂
L
: L → V.
Якщо iснують пари вершин v
1
, v
2
для яких iснують m ребер e : ∂
E
(e) =
{v
1
, v
2
} i m > 1, то говорять про наявнiсть кратних ребер. Iнодi говорять, що
вершини v
1
, v
2
мають спiльне ребро кратностi m.
Означення 7.0.3. Граф без кратних ребер та петель називається простим.
Простий граф визначається трiйкою (V, E, ∂
E
).
Приклад 7.0.1. Прикладами простих графiв є цiлком незв’язний граф у
якого E = ∅, тобто граф, у якого немає жодного ребра. Протилежним при-
кладом є повний граф, у якого будь-якi двi вершини з’єднанi ребром.
Питання. Скiльки ребер має повний граф на n вершинах?
111
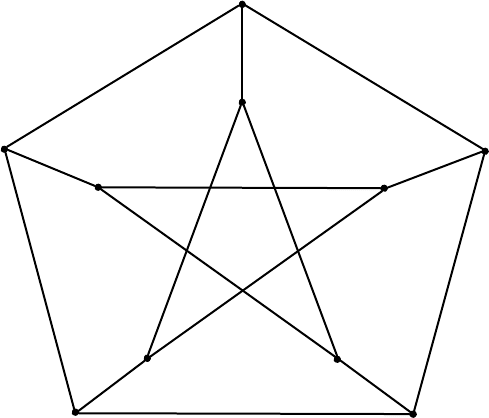
Приклад 7.0.2. Наведемо ще декiлька важливих прикладiв.
Означення 7.0.4. i) В орiєнтованому (неорiєнтованому) графi вершини v
1
, v
2
називаються сумiжними, якщо iснує ребро
e ∈ E : ∂
E
(e) = (v
1
, v
2
) (∂
E
(e) = {v
1
, v
2
}),
при цьому говорять, що ребро e є iнцидентним як вершинi v
1
так i
вершинi v
2
.
ii) В орiєнтованому (неорiєнтованому) графi ребра e
1
, e
2
називаються сумi-
жними, якщо впорядкованi пари ∂
E
(e
1
), ∂
E
(e
2
) мають спiльнi координа-
ти ( множини ∂
E
(e
1
) i ∂
E
(e
2
) мають спiльну вершину).
iii) Вершина v та ребро e називаються iнцидентними, якщо ребро e є iнци-
дентним вершинi v.
iv) Вершина v та петля l називаються iнцидентними, якщо ∂
L
(l) = v.
Означення 7.0.5. Кiлькiсть ребер iнцидентних данiй вершинi v плюс подво-
єна кiлькiсть iнцидентних їй петель називають степенем або валентнiстю
вершини i позначають deg v
Означення 7.0.6. Простий граф називається регулярним, якщо всi його
вершини мають однаковий степiнь.
Приклад 7.0.3. Прикладами регулярних графiв є правильнi многогранники -
тетраедр, куб, октаедр iкосаедр, додекаедр. В рiзних задачах часто виникає
граф Петерсона:
Як бачимо, кожна вершина цього графу має степiнь 3.
112

Лема 7.0.1. (про рукопотискання). Для довiльного графу G = (V, E, L, ∂
E
, ∂
L
)
має мiсце
X
v∈V
deg v = 2(|E| + |L|). (7.1)
Доведення. Пiдрахуємо кiлькiсть ребер iнцидентних рiзним вершинам i пiдсу-
муємо цi числа по всiм вершинам. Очевидно, що ми отримаємо подвоєну кiль-
кiсть ребер графа. Адже кожне ребро iнцидентне двом вершинам, а отже буде
враховано два рази. Оскiльки степiнь кожної вершини є сумою кiлькостi iнци-
дентних їй ребер та подвоєної кiлькостi петель, то цим лема доведена.
Назва леми пов’язано з наступною iнтерпретацiєю. Нехай є певна кiлькiсть
людей, з кожним з яких ми зв’яжемо вершину графа. Двi вершини будуть сумi-
жними, якщо цi люди потискали один одному руку. Цiлком можливо iснування
пар, якi привiталися декiлька разiв (таке буває коли забули про те, що сьогоднi
вже вiталися), менш ймовiрно (хоча чого не буває), що якась людина привiтала-
ся сама з собою. При такiй iнтерпретацiї, в правiй частинi рiвностi (7.1) стоїть
подвоєна загальна кiлькiсть рукопотискань, що вiдбулися, а у лiвiй пiдсумову-
ються кiлькостi рукопотискань зроблених усiма особами.
Означення 7.0.7. Для даного орiєнтованого (неорiєнтованого) графа можна
скласти матрицю сумiжностi
v
1
v
2
v
3
. . . v
n
v
1
∗ ∗ ∗ . . . ∗
v
2
∗ ∗ ∗ . . . ∗
v
3
∗ ∗ ∗ . . . ∗
. . . . . . . . . . . . . . . . . .
v
n
∗ ∗ ∗ . . . ∗
,
Де на перетинi рядка та стовпчика, що вiдповiдають вершинам v
i
, v
j
(v
i
6=
v
j
) стоїть число * — ребер e : ∂
E
(e) = (v
i
, v
j
), а на дiагоналi стоять кiлькостi
петель l iнцидентних вiдповiднiй вершинi v, тобто ∗ = |{l ∈ L|∂(l) = v}|.
Для неорiєнтованого графа ∗ буде означати кiлькiсть ребер e : ∂
E
(e) =
{v
i
, v
j
} i матриця сумiжностi буде симетричною вiдносно дiагоналi.
Для простого графа будемо мати матрицю з нулiв та одиниць з нульовою
дiагоналлю.
Означення 7.0.8. Для простих графiв розглядають також реберну матри-
113

цю сумiжностi:
e
1
e
2
e
3
. . . e
n
e
1
∗ ∗ ∗ . . . ∗
e
2
∗ ∗ ∗ . . . ∗
e
3
∗ ∗ ∗ . . . ∗
. . . . . . . . . . . . . . . . . .
e
n
∗ ∗ ∗ . . . ∗
,
де ∗ дорiвнює 1, якщо вiдповiднi ребра сумiжнi i 0, в протилежному випадку.
Означення 7.0.9. Для неорiєнтованих графiв може бути корисною матриця
iнцидентностi:
e
1
e
2
e
3
. . . e
n
v
1
∗ ∗ ∗ . . . ∗
v
2
∗ ∗ ∗ . . . ∗
v
3
∗ ∗ ∗ . . . ∗
. . . . . . . . . . . . . . . . . .
v
m
∗ ∗ ∗ . . . ∗
,
де ∗ дорiвнює 1, якщо вiдповiдна вершина та ребро iнцидентнi i 0, в протиле-
жному випадку.
Означення 7.0.10. Два простих графа G
1
= (V
1
, E
1
, ∂
E
1
), G
2
= (V
2
, E
3
, ∂
E
2
)
називаються iзоморфними, якщо iснує бiєкцiя мiж множинами вершин:
φ : V
1
↔ V
2
,
така, що
вершини v, v
1
∈ V
1
сумiжнi ⇔ вершини φ(v), φ(v
1
) ∈ V
2
сумiжнi
Розглянемо два графи G
1
i G
2
.
1
2
3
4
5
6
114
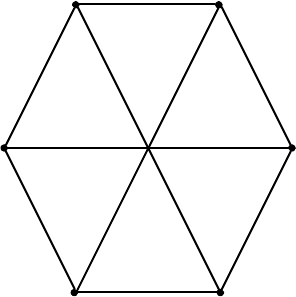
a
b
c
de
f
Обидва вони є регулярними графами степеня 3 i як бачимо картинки суттєво
рiзняться, але насправдi цi графи iзоморфнi. Iзоморфiзм визначає наступна бi-
єкцiя φ :
1 7→ a
2 7→ c
3 7→ e
4 7→ f
5 7→ d
6 7→ b
Завдання. Побудуйте ще декiлька iзоморфiзмiв мiж цими графами.
Наведенi графи є прикладами так званих дводольних графiв.
Означення 7.0.11. Граф називається дводольним, якщо множину його
вершин можна розбити на двi пiдмножини (долi) V
1
, V
2
таким чином, що
жодна двi вершини з однiєї долi не є сумiжними.
Питання. За яких умов цикл є дводольним графом?
Для загальних графiв означення iзоморфiзму бiльш складне. Адже треба
враховувати кратнiсть ребер та петель, а для орграфiв узгоджувати напрямки
ребер.
Означення 7.0.12. Графи G
1
= (V
1
, E
1
, L
1
, ∂
E
1
, ∂
L
1
), G
2
= (V
2
, E
2
, L
2
, ∂
E
2
, ∂
L
2
),
називаються iзоморфними, якщо iснують бiєкцiї:
φ : V
1
↔ V
2
, ψ
1
: E
1
↔ E
2
, ψ
2
: L
1
↔ L
2
такi, що
∂
E
2
(ψ
1
(e)) = φ(∂
E
1
(e))
∂
L
2
(ψ
2
(l)) = φ(∂
E
1
(l)).
115

В правiй частинi першої рiвностi стоїть упорядкована або неупорядкована
пара вершин, яка отримана застосуванням вiдображення φ до кожного елемента
пари вершин ∂
E
1
(e).
7.1 Операцiї над графами.
1. Об’єднанням графiв G
1
= (V
1
, E
1
, L
1
, ∂
E
1
, ∂
L
1
), G
2
= (V
2
, E
2
, L
2
, ∂
E
2
, ∂
L
2
),
якi не мають спiльних вершин (V
1
∩ V
2
= ∅), а отже i ребер (E
1
∩ E
2
= ∅)
називається граф
G
1
∪ G
2
= (V
1
∪ V
2
, E
1
∪ E
2
, L
1
∪ L
2
, ∂
E
1
∪E
2
, ∂
L
1
∪L
2
),
у якого
∂
E
1
∪E
2
(e) =
½
∂
E
1
(e) якщо e ∈ E
1
∂
E
2
(e) якщо e ∈ E
2
∂
L
1
∪L
2
(l) =
½
∂
L
1
(l) якщо l ∈ L
1
∂
L
2
(l) якщо l ∈ L
2
Означення 7.1.1. Граф називається зв’язним, якщо його не можна подати
як об’єднання двох графiв.
2. З’єднанням (конкатинацiєю) графiв
G
1
= (V
1
, E
1
, L
1
, ∂
E
1
, ∂
L
1
), G
2
= (V
2
, E
2
, L
2
, ∂
E
2
, ∂
L
2
), якi не мають спiльних вер-
шин (V
1
∩ V
2
= ∅), а отже i ребер (E
1
∩ E
2
= ∅) називається граф
G
1
∪ G
2
= (V
1
∪ V
2
, E
1
∪ E
2
∪ E
12
, L
1
∪ L
2
, ∂
E
1
∪E
2
∪E
12
, ∂
L
1
∪L
2
),
при цьому множина нових ребер E
12
така, що
∀v
1
∈ V
1
, v
2
∈ V
2
∃!e ∈ E
1,2
: ∂
E
1
∪E
2
∪E
12
(e) = {v
1
, v
2
}.
2. Доповненням простого графа G = (V, E, ∂
E
) називається граф G =
(V,
e
E, ∂
E
), такий, що довiльна пар вершин є сумiжними в графi G тодi i тiльки
тодi, коли вони не є сумiжними в графi G.
7.2 Маршрути, ланцюги, цикли.
Означення 7.2.1. Нехай G− загальний неорiєнтований граф, пара вершин
v
1
, v
m
та скiнченна послiдовнiсть ребер e
1
, e
2
, . . . , e
m
: називається маршру-
том (шляхом) мiж вершинами v
1
, v
m
, якщо
v
1
iнцидентна e
1
, v
m
iнцидентна e
m
, а послiдовнi пари ребер e
i−1
, e
i
є су-
мiжними для довiльного i : 1 < i ≤ m. При цьому вершина v
1
i називається
початком маршруту, а v
m
її кiнцем.
116

Для орiєнтованих графiв слiд вимагати, щоб кiнець ребра e
i−1
збiгався з
початком ребра e
i
.
Якщо всi ребра маршруту є рiзними, то маршрут називають ланцюгом,
а якщо початок i кiнець ланцюга збiгаються, то ланцюг називається за-
мкненим або циклом.
Якщо всi вершини, що iнцидентнi ребрам ланцюга, з’являються лише один
раз, тобто кожна вершина є iнцидентною ребрам лише одної пари e
i−1
, e
i
,
крiм можливо початку та кiнця, якi можуть i збiгатися, то такий ланцюг
будемо називати простим.
Простий замкнений ланцюг називається простим циклом.
Лема 7.2.1. Якщо в скiнченному графi степiнь кожної вершини графа не мен-
ша нiж 2, то граф має принаймнi один цикл.
Доведення. Оберемо довiльну вершину вiдмiтимо її (наприклад "пофарбуємо")
i "пiдемо"по довiльному iнцидентному їй ребру (воно iснує бо степiнь вершини
не менша нiж 2). Досягши сумiжної вершини вiдмiтимо її i "пiдемо"далi по
iншому ребру, яке iснує внаслiдок умови на степiнь вершини. При такiй прогу-
лянцi, якщо ми приходимо у вершину, в якiй ще не були, то завжди є iнше ребро,
по якому можна вийти. Але оскiльки граф має скiнченну кiлькiсть вершин, то
рано чи пiзно ми попадемо у вершину, в якiй були ранiше, i цим побудуємо
цикл.
На множинi вершин графа G можна розглянути вiдношення: v
1
∼ v
2
тодi
i лише тодi, коли iснує маршрут з початком у вершинi v
1
i кiнцем у вершинi
v
2
. Самостiйно переконайтеся, що це вiдношення є вiдношенням еквiвалентно-
стi. Очевидно, що вершини, якi належать рiзним класам еквiвалентностi, є не
сумiжними. Отже, граф G можна подати як об’єднання
G =
k
[
i=1
G
i
,
де G
i
− граф множина вершини якого збiгається з певним класом еквiвален-
тностi, разом з iнцидентними їм ребрами. При цьому, очевидно, що графи G
i
будуть зв’язними. Вони називаються компонентами зв’язностi графа G. У
зв’язного графа є лише одна компонента зв’язностi.
Означення 7.2.2. Ребро графа називається мостом, якщо пiсля його вилуче-
ння кiлькiсть компонент зв’язностi збiльшується.
Зауважимо, що жодне ребро, що входить у замкнений ланцюг не є мостом.
117

Теорема 7.2.1. Нехай G = (V, E, ∂
E
)− простий граф з n = |V | вершинами,
m = |E| ребрами та k компонентами зв’язностi. Тодi мають мiсце наступнi
нерiвностi.
n − k ≤ m ≤
(n − k)(n − k + 1)
2
(7.2)
Доведення. Доведення нерiвностi n − k ≤ m проведемо методом математичної
iндукцiї по числу ребер.
База iндукцiї — m = 0. Маємо цiлком незв’язний граф (кiлькiсть компонент
дорiвнює кiлькостi вершин n = k), отже n − n = 0 i базу доведено.
Припустимо, що нерiвнiсть доведено для графiв з кiлькiстю ребер меншою
за m. Оберемо довiльне ребро графа i вилучаємо його з графа залишивши всi
вершини i решту ребер. При цьому можливi два випадки:
i) кiлькiсть компонент зв’язностi не змiнилася i дорiвнює k;
ii) кiлькiсть компонент зв’язностi збiльшилася i дорiвнює k + 1.
Оскiльки кiлькiсть ребер у отриманого графа дорiвнює m − 1, то за припу-
щенням iндукцiї у випадку i) будемо мати: n − k ≤ m − 1, а отже, n − k < m.
У випадку ii) отримуємо n − (k + 1) ≤ m − 1, звiдки n − k ≤ m.
Для доведення другої нерiвностi в графi G =
S
k
i=1
G
i
оберемо компоненту
зв’язностi з найбiльшою кiлькiстю вершин. Якщо таких декiлька, то одну з них.
Не втрачаючи загальностi можна вважати, що це G
1
. Для довiльної компоненти
G
i
, що мiстить бiльше нiж одну вершину, виконаємо таку операцiю:
1) виберемо довiльну вершину i вилучимо її разом з усiма ребрами, що їй
iнцидентнi;
2) додамо у компоненту G
1
одну вершину i стiльки ребер, щоб ця вершина
стала сумiжною до будь-якої вершини з цiєї компоненти.
Очевидно, що при цьому кiлькiсть вершин та кiлькiсть компонент зв’язностi у
нового графа залишаться не змiнними, а кiлькiсть ребер принаймнi не зменши-
ться (згадаємо, що G
1
мiстить максимальну кiлькiсть вершин). Цю процедуру
будемо повторювати до тих пiр доки в компонентi G
i
не залишиться одна вер-
шина i не буде жодного ребра. Повторивши цю процедуру з усiма компонента-
ми G
i
, i > 1, ми отримаємо граф на n вершинах з k компонентами зв’язностi,
причому всi вони, крiм першої, складаються з однiєї iзольованої вершини. Тодi,
кiлькiсть вершин першої компоненти дорiвнює n−(k−1). Максимально можли-
ва кiлькiсть ребер у такого графа буде тодi, коли ця компонента буде повним
графом. Тодi число ребер такого графа буде дорiвнювати: C
2
n−k+1
=
(n−k)(n−k+1)
2
,
що i треба було довести.
118
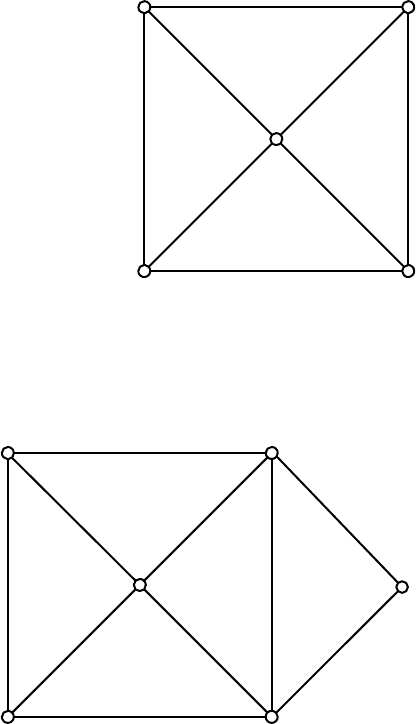
7.3 Ейлеровi графи.
Нехай G = (V, E, L, ∂
E
, ∂
L
)− загальний неорiєнтований граф.
Означення 7.3.1. Замкнений ланцюг графа, G, що мiстить всi ребра графа
називається ейлеровим; граф що має ейлеровий цикл називається ейлеро-
вим; граф, що мiстить ланцюг, що проходить через усi ребра називається
напiвейлеровим.
Вкажiть якi з цих графiв є ейлеровими та напiвейлеровими.
119

Теорема 7.3.1. Скiнченний зв’язний граф G є ейлеровим тодi i лише тодi,
коли степiнь кожної його вершини парна.
Доведення. ⇒ . Якщо граф є ейлеровим, то iснує ейлеровий цикл. Оскiльки вiн
мiстить усi вершини, то для кожної з них iнцидентнi їй ребра розбиваються на
пари ( вхiдне, вихiдне ребра,). При цьому для початкової вершини i першого
ребра циклу iснує ребро по якому ми повернулись в неї. Цим необхiднiсть умови
доведена.
⇐ . Доведення достатностi проведемо методом математичної iндукцiї по
кiлькостi ребер графа. Якщо граф ребер не мiстить ребер, то вiн складається
з однiєї iзольованої вершини i твердження тривiальне. Припустимо, що граф
G має m ребер i для графiв з меншою кiлькiстю ребер твердження має мiсце.
Оскiльки степiнь кожної вершини графа G не менша нiж 2 (умова парностi сте-
пеня), то за лемою 7.2.1 в ньому iснує цикл. Тимчасово вилучаємо ребра цього
циклу (запам’ятавши вершини якi утворювали цикл). Кожна вершина отрима-
ного графа
˜
G має парний степiнь, адже з кожної вершини циклу вилучалась
пара ребер. Тодi кожна компонента зв’язностi графа
˜
G =
S
k
i=1
G
i
задовольняє
умовi твердження, а оскiльки кожна з них має меншу кiлькiсть ребер, то мо-
жна застосувати припущення iндукцiї i в кожнiй з них побудувати ейлеровий
цикл. Тепер вiдновимо заново граф G. Початкова вершина циклу належить до
вiдповiдної компоненти G
i
i ми рухаємося по побудованому ранiше ейлеровому
циклу i вертаємося в цю ж вершину. Пiсля цього по ребру циклу переходимо в
наступну вершину. Якщо ця вершина належить тiй самiй компонентi зв’язностi
G
i
, що i попередня, то продовжуємо рух по ребру цикла. Якщо ж ми попали
в iншу компоненту G
k
, то проходимо її по ранiше побудованому ейлеровому
циклу i вертаємося в цю ж вершину. Продовжуючи цей процес ми повернемося
в початкову вершину i пройдемо кожне ребро графа G по одному разу. Таким
чином буде побудовано ейлеровий цикл всього графа G.
120
