Бобриков C.А. Математические основы теории систем
Подождите немного. Документ загружается.

При известной передаточной функции системы K(P) и известной спектральной
плотности Sх() стационарного случайного сигнала X(t), действующего на входе
системы, по формуле (12) можно найти спектральную плотность стационарного
случайного сигнала на выходе системы.
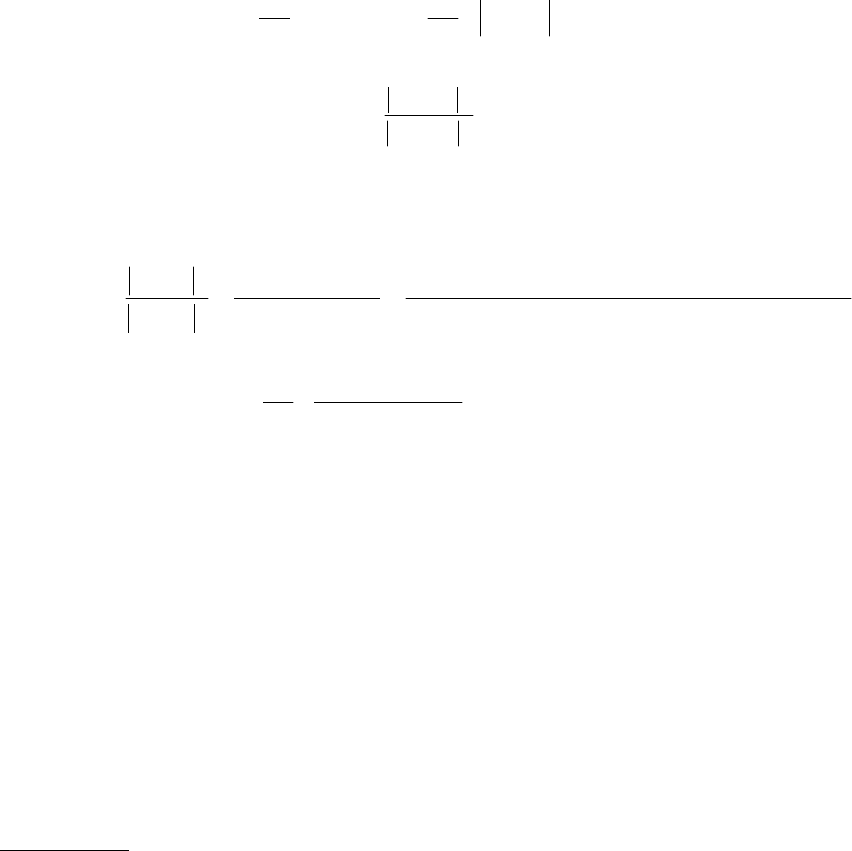
Дисперсия выходного сигнала равна
D S d K j S d
y y x
= =
1
2
1
2
2
.
(13)
Подынтегральное выражение в формуле (13) имеет вид:
B j
A j
2
2
,
где А(j) и В(j) представляют собой полиномы от комплексной переменной j.
Обозначим наивысшую степень знаменателя через 2n. Наивысшая степень числителя
для реальных систем может быть не более 2n-2. Для интегрирования по формуле (13)
подынтегральное выражение представляют в следующей форме:
B j
A j
G j
A j A j
b j b j b
a j a j a a j a
n n
n
n n
n n
2
2
0
2 2
1
2 4
1
0 1
1
0
= =
...
... ...
.
Откуда
D
G j
A j A j
d In
y
= =
1
2
Интегралы In для различных значений n приведены в справочниках и учебниках по
теории автоматического управления.
Математическое ожидание m
y
стационарного случайного сигнала у(t) на выходе
линейной системы с передаточной функцией K(P) связано с математическим
ожиданием m
х
стационарного случайного сигнала Х(t) на входе системы следующей
формулой:
m
y
=K(0)m
x
, где K(0)=K(P) при Р=0.
Литература
1. Бессекерский В.А., Попов Е.П. Теория систем автоматического регулирования. -
М.: Наука, 1972.- 767 с.; ил.
2. Солодовников В.В. Статистическая динамика линейных систем автоматического
управления. - М.: Физматгиз, 1960 с.;ил.
81
