Blanchet L., Spallicci A., Whiting B. (Eds.) Mass and Motion in General Relativity
Подождите немного. Документ загружается.

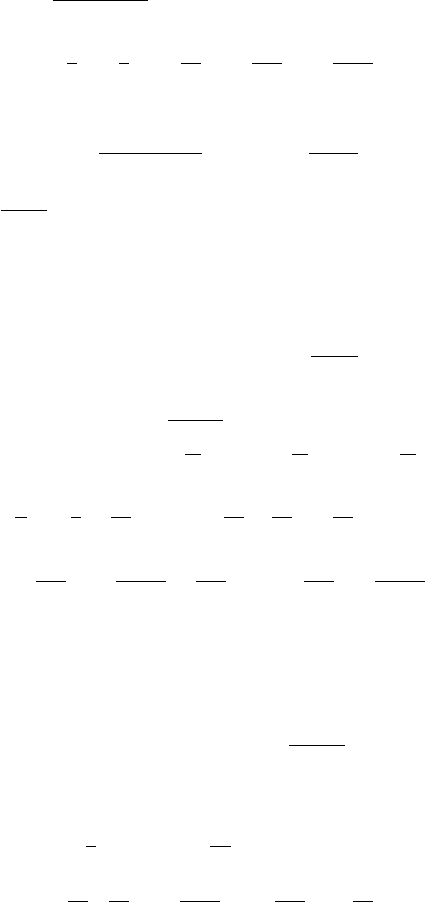
Post-Newtonian Methods: Analytic Results on the Binary Problem 191
O
H.x/ D
1 2x
.1 3x/
1=2
1
D
1
2
x C
3
8
x
2
C
27
16
x
3
C
675
128
x
4
C
3969
256
x
5
C; (126)
where
O
H.x/
H.x/ mc
2
mc
2
;xD
GM !
c
3
2=3
: (127)
The condition
d
O
H.x/
dx
D 0 yields x D 1=6 0:167 or, in Schwarzschild coordinates
R D 6GM=c
2
. Evidently, ISCOs are located close to the reliability limit of PN
expansions [20].
Using the dynamical invariants, the angular frequency of circular motion can be
written as
!
circ
D !
radial
C !
periastron
D 2
1 C k
P
: (128)
With the aid of the definition x D
GM !
circ
c
3
2=3
, the binary dynamics yield, through
3PN order, that is, c
2
O
H
3PN
D
Q
H
N
C
1
c
2
Q
H
Œ1PN
C
1
c
4
Q
H
Œ2PN
C
1
c
6
Q
H
Œ3PN
,
O
H
3PN
.x/ D
x
2
C
3
8
C
1
24
x
2
C
27
16
19
16
C
1
48
2
x
3
C
675
128
C
34445
1152
C
205
192
2
C
155
192
2
C
35
10368
3
x
4
: (129)
The ISCO, calculated with the aid of Eq. 125, turns out to be x 0:255 [3,32].
To likely improve the PN truncation a representation of the energy is helpful,
which in the test-particle limit is known to be a ratio of two simple polynomials for
example,
e .1 C
O
H/
2
1 Dx
1 4x
1 3x
(130)
For the binary 3 PN Hamiltonian, e turns out to be
e.x/ Dx
1
1
1
3
x
3
35
12
x
2
9 C
5
24
41
4
2
4309
15
C
103
36
2
1
81
3
x
3
C
: (131)
Applying to this expression the technique of pad´eing, that is, putting it on a
ratio-of-polynomials footing, the ISCO turned out to be, for equal-mass binaries,
x 0:198 [20].
To make contact to a recent discussion about the existence or nonexistence of
ISCOs for equal-mass binaries in a PN setting [12], we discuss the more general

192 G. Sch¨afer
stability conditions for noncircular orbits using the Hamiltonian H.r;p
r
;J/,where
J D p
'
. The crucial conditions for stability are
.1/ W
@
2
H
@r
2
>0; .2/W
@
2
H
@p
2
r
>0; .3/W
@
2
H
@r
2
@
2
H
@p
2
r
>0: (132)
Instability occurs if one of the >-signs turns to zero. This particularly means that the
>-sign in .3/ has to be zero. On the other side, in approximation calculations, where
truncated series occur, the expression .3/ can be zero without one of the expressions
.1/ or .2/ being zero because the product of two series of the order n PN, which
is of order 2n PN, is again truncated at n PN and thus can be zero without one or
both of the factors being zero. In Ref. [12] the condition .3/ has been given priority
because it turned out to be coordinate invariant through 3 PN order (notice in this
regard, p
r
D @W =@r,whereW is an action).
4.4 PN Dissipative Binary Dynamics
The leading order 2.5 PN dissipative binary orbital dynamics is described by the
nonautonomous Hamiltonian, [65],
H
Œ2:5PN
.t/ D
2G
5c
5
d
3
Q
ij
.t/
dt
3
p
1i
p
1j
m
1
C
p
2i
p
2j
m
2
Gm
1
m
2
r
12
; (133)
where
Q
ij
.t/ D
X
aD1;2
m
a
.x
0i
a
x
0j
a
1
3
x
02
a
ı
ij
/ (134)
is the Newtonian mass-quadrupole tensor. Evidently, only after the Hamilton
equations of motion are calculated the primed position and momentum variables
resulting via Q
ij
.t/ from time differentiations and use of the equations of motion
are allowed to be identified with the unprimed position and momentum variables.
The 3.5 PN Hamiltonian is known too, but it will not be given here because of
quite lengthy expressions [45]. Applications of the 2.5 PN Hamiltonian can be
found in, for example, [17, 37, 50, 63], where in Ref. [37] a transformation to the
Burke–Thorne gauge (coordinate conditions) is performed.
5 Toward Binary Spinning Black Holes
Within the ADM formalism the action functional (i.e., the integral of the
Lagrangian) of rotating bodies must have the following structure as long as the
lengths of the spins are preserved in time,

Post-Newtonian Methods: Analytic Results on the Binary Problem 193
W D
Z
dt
X
a
p
ai
Px
i
a
C
X
a
S
.i/
a
˝
.i/
a
C
c
3
16G
Z
d
3
x
ij
TT
P
h
TT
ij
H
ADM
h
x
i
a
;p
ai
;S
.j /
a
;h
TT
ij
;
ij
TT
i
!
: (135)
Here, ˝
.i/
a
D˝
a.i/
D
1
2
ij k
a.l/.j /
P
a.l/.k/
,
a.i/.k/
a.j /.k/
D
a.k/.i /
a.k/.j /
D
ı
ij
,
ij k
D.i j /.j k/.ki/=2;andp
ai
, x
i
a
, S
.i/
a
DS
a.i/
,andı
.i/
a
D
1
2
ij k
a.l/.j /
ı
a.l/.k/
are the independent matter variables, where the index a again numerates
the particles. Notice that
.i/
a
are anholonomic variables related to the angle-type
variables
a.i/.j /
of the proper rotations (spins). ˝
.i/
a
is the spin precession angular
frequency vector of the ath particle. The equations of motion for the particles read,
Px
i
a
.t/ D
ı
R
dt
0
H
ADM
ıp
ai
.t/
; Pp
ai
.t/ D
ı
R
dt
0
H
ADM
ıx
i
a
.t/
; (136)
˝
.i/
a
.t/ D
ı
R
dt
0
H
ADM
ıS
.i/
a
.t/
;
P
S
.i/
a
.t/ D
ij k
˝
.j /
a
.t/S
.k/
a
.t/; (137)
where the last equation results from the action functional through variation with
respect to
.i/
a
; for more details, see, for example, [39]. The Hamiltonian that gener-
ates both the evolution equations for all dynamical variables as well as the constraint
equations through variation with respect to the Lagrange multipliers, the lapse and
shift functions N and N
i
, respectively, is given by
H D
Z
d
3
x.N H N
i
H
i
/ CEŒ
ij
; (138)
where
EŒ
ij
D
c
4
16G
I
i
0
ds
i
.
ij;j
jj;i
/ (139)
is a surface integral at spacelike infinity i
0
with ds
i
the two-dimensional surface-
area element, [61], and
H D H
field
C H
matter
; (140)
H
i
D H
field
i
C H
matter
i
; (141)
with
16G
c
4
H
field
D
1=2
R C
1
1=2
i
j
j
i
1
2
i
i
j
j
; (142)
16G
c
3
H
field
i
D 2@
j
j
i
C
kl
@
i
kl
; (143)

194 G. Sch¨afer
are the total Hamilton and (linear) momentum densities. After imposing the
constraint equations H D H
i
D 0 and the coordinate conditions (32–34), the
energy expression EŒ
ij
turns into the ADM-Hamiltonian,
EŒ
ij
D H
h
x
i
a
;p
ai
;S
.i/
a
;h
TT
ij
;
ij
TT
i
: (144)
To linear order in the spin variables, the matter densities read (recall, ı
a
D ı.x
x
a
/; on simplicity reasons the index a will not show up in the following equations)
H
matter
D.np/cı
c
2
t
k
ij
ij
;k
cp
l
mc np
ij
kl
O
S
jk
ı
;i
; (145)
H
matter
i
D p
i
ı C
1
2
h
mk
O
S
ik
ı
i
;m
p
l
p
k
np .mc np /
.
mk
ı
p
i
C
mp
ı
k
i
/
ql
O
S
qp
ı
;m
; (146)
with
np n
p
D
m
2
c
2
C
ij
p
i
p
j
1=2
(147)
and
t
k
ij
D
kl
O
S
l.i
p
j/
np
ı C
kl
mn
O
S
m.i
p
j/
p
n
p
l
.np/
2
.mc np /
ı; (148)
where n
is the future directed unit vector field orthogonal to the t D const hyper-
surfaces, n
D .N; 0; 0; 0/. The above expressions were shown to be correct up to
(and including) the orders S=c
4
and S=c
2
in H
matter
and H
matter
i
, respectively.
Introducing a dreibein field e
.i/
j
with e
.i/
j
e
.i/
k
D
jk
and e
.i/k
e
k
.j /
D ı
ij
,aspin
tensor S
.k/.l/
D e
i
.k/
e
j
.l/
O
S
ij
can be introduced that fulfills the relation
ik
jl
O
S
ij
O
S
kl
D 2S
.i/
S
.i/
D const; (149)
where 2S
.i/
D
ij k
S
.j /.k/
. Crucial for our canonical formalism is the constancy in
time of S
.i/
S
.i/
. Because of the symmetry property of the metric coefficients
ij
,the
symmetric root of
ij
e
il
e
lj
D
ij
;e
ij
D e
ji
(150)
can be taken for the dreibein field, that is, e
.j /k
D e
jk
.

Post-Newtonian Methods: Analytic Results on the Binary Problem 195
To the order the formalism has been developed consistently, the following
relations hold,
p
ai
D
Z
V
a
d
3
xH
matter
i
; (151)
J
aij
D
Z
V
a
d
3
x.x
i
H
matter
j
x
j
H
matter
i
/ D x
i
a
p
aj
x
j
a
p
ai
C S
a.i/.j /
; (152)
where V
a
denotes the volume of particle a.Furthermore,
fx
i
a
;p
aj
gDı
ij
; fS
a.i/
;S
a.j /
gD
ij k
S
a.k/
; zero otherwise; (153)
and the total linear and angular momenta, respectively, take the forms P
i
D
P
a
p
ai
and J
ij
D
P
a
J
aij
.
The crucial consistency relation reads,
ıH
matter
ı
ij
D
c
2
N
p
T
ij
(154)
with
H
matter
D
Z
d
3
x.N H
matter
N
i
H
matter
i
/: (155)
It is fulfilled to the needed order,
p
T
ij
D
p
i
p
j
np
ı C t
k
ij;k
C O.G/: (156)
In asymptotically flat spacetimes the Poincar´e group is a global symmetry group.
Its generators P
and J
are conserved and fulfill the Poincar´e algebra, see, for
example, [61],
fP
;P
gD0; (157)
fP
;J
gD
P
C
P
; (158)
fJ
;J
gD
J
C
J
C
J
J
: (159)
The meaning of the components are energy P
0
DH=c, linear momentum P
i
DP
i
,
angular momentum J
ij
DJ
ij
, and Lorentz boost J
i0
=c K
i
DG
i
tP
i
. A center-
of-mass vector can be defined by X
i
Dc
2
G
i
=H . This vector, however, is not a
canonical position vector, see, for example, [39]. The energy H and the center-of-
mass vector G
i
D G
i
have the representations
H D
c
4
16G
Z
d
3
x D
c
4
16G
I
i
0
r
2
d˝nr; (160)
G
i
D
c
2
16G
Z
d
3
x x
i
D
c
2
16G
I
i
0
r
2
d˝n
j
.x
i
@
j
ı
ij
/; (161)

196 G. Sch¨afer
where i
0
denotes spacelike infinity, r
2
d˝n is the two-dimensional surface-area
element, and n the radial unit vector. The two quantities, H; G
i
, are the most in-
volved ones of those entering the Poincar´ealgebra.
In terms of three-dimensional quantities, the Poincar´e algebra reads, see, for
example [21], with J
ij
D
ij k
J
k
,
fP
i
;HgDfJ
i
;HgD0; (162)
fJ
i
;P
j
gD"
ij k
P
k
; (163)
fJ
i
;J
j
gD"
ij k
J
k
; (164)
fJ
i
;G
j
gD"
ij k
G
k
; (165)
fG
i
;HgDP
i
; (166)
fG
i
;P
j
gD
1
c
2
Hı
ij
; (167)
fG
i
;G
j
gD
1
c
2
"
ij k
J
k
: (168)
The Poincar´e algebra has been extensively used in the calculations of PN Hamilto-
nians for spinning binaries [40,41]. Hereby the most important equation was (166),
which tells that the total linear momentum has to be a total time derivative. Once
this equation has even fixed the kinetic ambiguity in nondimensional regularization
calculations [21]. The kinetic ambiguity got also fixed by a Lorentzian version of
the Hadamard regularization based on the Fock-de Donder approach [10].
5.1 Approximate Hamiltonians for Spinning Binaries
All the Hamiltonians, and the center-of-mass vectors too, given in this section have
been derived or rederived in recent papers by the author and his collaborators em-
ploying general relativity in canonical form [25, 40, 41, 67, 69], adjusting it to the
motion of binary black holes.
The Hamiltonian of leading-order (LO ) spin–orbit coupling reads
H
LO
SO
D
X
a
X
b¤a
G
c
2
r
2
ab
.S
a
n
ab
/
3m
b
2m
a
p
a
2p
b
; (169)
and the one of leading-order spin(1)–spin(2) coupling is given by
H
LO
S
1
S
2
D
X
a
X
b¤a
G
2c
2
r
3
ab
Œ3.S
a
n
ab
/.S
b
n
ab
/ .S
a
S
b
/ ; (170)
where r
ab
n
ab
Dx
a
x
b
, a ¤b,anda; b D1; 2. The more complicated Hamiltonian
is the one with spin-squared terms because it relates to the rotational deformation of
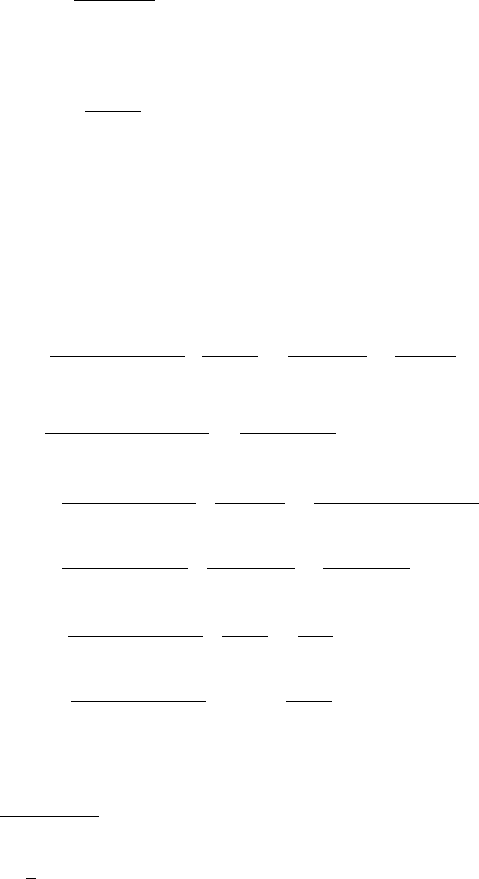
Post-Newtonian Methods: Analytic Results on the Binary Problem 197
spinning black holes. To leading order, say for spin(1), it reads (details of derivation
are given later)
H
LO
S
2
1
D
Gm
2
2c
2
m
1
r
3
12
Œ3.S
1
n
12
/.S
1
n
12
/ .S
1
S
1
/ : (171)
The LO spin–orbit and spin(a)–spin(b) center-of-mass vectors take the form
G
LO
SO
D
X
a
1
2c
2
m
a
.p
a
S
a
/; G
LO
S
1
S
2
D 0; G
LO
S
2
1
D 0: (172)
Within the conservative 3 PN dynamics for spinless point masses, the center-of-mass
vector has been calculated in [21]. Applications of the LO spin Hamiltonians can
be found in, for example, [2,18,66]. Other references treating the LO spin dynam-
ics are, for example, [29, 49, 60, 71]. For applications of the next-to-leading-order
(NLO) spin dynamics, presented straight below, see, for example, [5,26].
The Hamiltonian of the NLO spin–orbit coupling reads, r D r
12
,
H
NLO
SO
DG
..p
1
S
1
/ n
12
/
c
4
r
2
"
5m
2
p
2
1
8m
3
1
C
3.p
1
p
2
/
4m
2
1
3p
2
2
4m
1
m
2
C
3.p
1
n
12
/.p
2
n
12
/
4m
2
1
C
3.p
2
n
12
/
2
2m
1
m
2
#
C G
..p
2
S
1
/ n
12
/
c
4
r
2
.p
1
p
2
/
m
1
m
2
C
3.p
1
n
12
/.p
2
n
12
/
m
1
m
2
C G
..p
1
S
1
/ p
2
/
c
4
r
2
2.p
2
n
12
/
m
1
m
2
3.p
1
n
12
/
4m
2
1
G
2
..p
1
S
1
/ n
12
/
c
4
r
3
11m
2
2
C
5m
2
2
m
1
C G
2
..p
2
S
1
/ n
12
/
c
4
r
3
6m
1
C
15m
2
2
C .1 $ 2/; (173)
and the one of NLO spin(1)–spin(2) coupling is given by
H
NLO
S
1
S
2
D
G
2m
1
m
2
c
4
r
3
Œ6..p
2
S
1
/ n
12
/..p
1
S
2
/ n
12
/
C
3
2
..p
1
S
1
/ n
12
/..p
2
S
2
/ n
12
/
15.S
1
n
12
/.S
2
n
12
/.p
1
n
12
/.p
2
n
12
/
3.S
1
n
12
/.S
2
n
12
/.p
1
p
2
/ C 3.S
1
p
2
/.S
2
n
12
/.p
1
n
12
/

198 G. Sch¨afer
C 3.S
2
p
1
/.S
1
n
12
/.p
2
n
12
/ C 3.S
1
p
1
/.S
2
n
12
/.p
2
n
12
/
C 3.S
2
p
2
/.S
1
n
12
/.p
1
n
12
/ 3.S
1
S
2
/.p
1
n
12
/.p
2
n
12
/
C .S
1
p
1
/.S
2
p
2
/
1
2
.S
1
p
2
/.S
2
p
1
/ C
1
2
.S
1
S
2
/.p
1
p
2
/
C
3
2m
2
1
r
3
Œ..p
1
S
1
/ n
12
/..p
1
S
2
/ n
12
/
C .S
1
S
2
/.p
1
n
12
/
2
.S
1
n
12
/.S
2
p
1
/.p
1
n
12
/
C
3
2m
2
2
r
3
Œ..p
2
S
2
/ n
12
/..p
2
S
1
/ n
12
/
C .S
1
S
2
/.p
2
n
12
/
2
.S
2
n
12
/.S
1
p
2
/.p
2
n
12
/
C
6.m
1
C m
2
/G
2
c
4
r
4
Œ.S
1
S
2
/ 2.S
1
n
12
/.S
2
n
12
/: (174)
The calculation of the LO and NLO order S
2
1
-Hamiltonians needs more information
about the source terms than given in Eqs. 145 and 146. To achieve the LO C NLO
S
2
1
-Hamiltonians, the following additional source in the Hamilton constraint is
needed,
H
matter
S
2
1
;static
D
1
2m
1
Q
ij
1
ı
1
Iij
C
1
8m
1
mn
pj
ql
mi
;p
nk
;q
O
S
1ij
O
S
1kl
ı
1
C
1
4m
1
ij
mn
kl
;m
O
S
1ln
O
S
1j k
ı
1
;i
; (175)
where; i and, i denote three-dimensional covariant and partial derivatives, respec-
tively, and where
Q
ij
1
ik
jl
mn
O
S
1km
O
S
1nl
C
2
3
S
2
1
ij
; (176)
2S
2
1
D
ik
jl
O
S
1ij
O
S
1kl
D const: (177)
Q
ij
1
is the quadrupole tensor of the black hole with number 1 resulting from its
rotational deformation. Herewith, beyond the previously shown LO Hamiltonian
(171), the NLO Hamiltonian comes out in the form, employing the Poincar´ealgebra
for unique fixation of all coefficients,
H
NLO
S
2
1
D
G
c
4
r
3
m
2
4m
3
1
.p
1
S
1
/
2
3
4m
1
m
2
p
2
2
S
2
1
C
3m
2
8m
3
1
.p
1
n/
2
S
2
1
3m
2
8m
3
1
p
2
1
.S
1
n/
2

Post-Newtonian Methods: Analytic Results on the Binary Problem 199
3m
2
4m
3
1
.p
1
n/.S
1
n/.p
1
S
1
/ C
9
4m
1
m
2
p
2
2
.S
1
n/
2
C
3
4m
2
1
.p
1
p
2
/ S
2
1
9
4m
2
1
.p
1
p
2
/.S
1
n/
2
3
2m
2
1
.p
1
n/.p
2
S
1
/.S
1
n/ C
3
m
2
1
.p
2
n/.p
1
S
1
/.S
1
n/
C
3
4m
2
1
.p
1
n/.p
2
n/ S
2
1
15
4m
2
1
.p
1
n/.p
2
n/.S
1
n/
2
G
2
m
2
2c
4
r
4
9.S
1
n/
2
5S
2
1
C
14m
2
m
1
.S
1
n/
2
6m
2
m
1
S
2
1
: (178)
The spin precession equations of the Hamiltonians H
NLO
SO
and H
NLO
S
2
1
have been
calculated also in the papers [57]and[58], respectively, where the first paper [57]
has benefited from paper [69]. The final spin precession equation of the second paper
[58], Eq. 60, deviates from the corresponding one in [67]. A detailed inspection has
shown that the last term in Eq. 62 of [58] has a wrong sign [68]. Using the correct
sign, after redefinition of the spin variable, agreement with the Hamiltonian of Ref.
[67] is achieved.
The NLO order spin–orbit and spin(a)–spin(b) center-of-mass vectors take the
form
G
NLO
SO
D
X
a
p
2
a
8c
4
m
3
a
.p
a
S
a
/
C
X
a
X
b¤a
m
b
G
4c
4
m
a
r
ab
..p
a
S
a
/ n
ab
/
5x
a
C x
b
r
ab
5.p
a
S
a
/
C
X
a
X
b¤a
G
c
4
r
ab
3
2
.p
b
S
a
/
1
2
.n
ab
S
a
/.p
b
n
ab
/
..p
b
S
a
/ n
ab
/
x
a
C x
b
r
ab
; (179)
G
NLO
S
1
S
2
D
G
2c
4
X
a
X
b¤a
Œ3.S
a
n
ab
/.S
b
n
ab
/ .S
a
S
b
/
x
a
r
3
ab
C .S
b
n
ab
/
S
a
r
2
ab
;
(180)
G
NLO
S
2
1
D
2m
2
G
c
4
m
1
"
3.S
1
n
12
/
2
8r
3
12
.x
1
C x
2
/ C
S
2
1
8r
3
12
.3x
1
5x
2
/
.S
1
n
12
/ S
1
r
2
12
#
I
(181)

200 G. Sch¨afer
summing up through 2 PN order in the spin parts, we obtain, also see [21],
G D G
N
CG
1PN
CG
2PN
CG
3PN
CG
LO
SO
CG
NLO
SO
CG
NLO
S
1
S
2
CG
NLO
S
2
1
CG
NLO
S
2
2
: (182)
Numerically, spins of black holes can be counted of order 1=c (maximum), thus the
spinless parts are taken up to the 3 PN order.
The currently known conservative binary Hamiltonians for spinning black holes
through order 1=c
4
can be summarized as follows
H D H
N
C H
1PN
C H
2PN
C H
3PN
CH
LO
SO
C H
LO
S
1
S
2
C H
LO
S
2
1
C H
LO
S
2
2
CH
NLO
SO
C H
NLO
S
1
S
2
C H
NLO
S
2
1
C H
NLO
S
2
2
CH
p
1
S
3
2
C H
p
2
S
3
1
C H
p
1
S
3
1
C H
p
2
S
3
2
CH
p
1
S
1
S
2
2
C H
p
2
S
2
S
2
1
C H
p
1
S
2
S
2
1
C H
p
2
S
1
S
2
2
CH
S
2
1
S
2
2
C H
S
1
S
3
2
C H
S
2
S
3
1
: (183)
The Hamiltonians H
S
4
1
and H
S
4
2
in the approximation in question turned out
to be zero.
6 Lorentz-Covariant Approach and PN Expansions
The Lorentz-covariant approach has found a quite thorough presentation in [4]. So
we will not go into so many details as in the canonical approach presented in the
previous sections.
The Einstein field equations are given by
G
.g
;@
˛
g
;@
˛
@
ˇ
g
/ D
8G
c
2
T
.g
Ic
2
/
c
2
; (184)
where g
and T
are the four-metric and the stress–energy tensor of the
matter (e.g., fluid), respectively. The contracted Bianchi identities yield the four-
dimensional equations of motion (EOM) for the matter,
r
G
0 !r
T
D 0 (EOM); (185)
