Библер В.С. Кант, Галилей, Кант. Разум нового времени в парадоксах самообоснования
Подождите немного. Документ загружается.


Однако логика причинная должна все же как-то присутствовать в "логике атрибутивной", логике
существования. Ведь ради того, чтобы рассчитать и сосредоточить силу, весь сыр-бор разгорелся, но
теперь внутри математики логика причинная должна "не жать в плечах",
не беспокоить...
Логико-онтологическая причинность превращается здесь в причинность формально-логическую, в связь
формальной последовательности, импликации. И совершается это просто. В недрах математики
совершать движение означает рассчитывать его и геометрически изображать (строить траекторию).
Движение материальной точки здесь замещается движением измерения и движением проведения
(построения) линии при помощи циркуля, лекала... Теоретик должен задним числом осуществить уже
осуществленное движение. Или иначе он должен представить совершающееся движение как
совершившееся.
Но это движение "задним числом" снова антиномично. Это — расчет, построение. Построение дает
траекторию как геометрический образ-континуум, как форму. Расчет (шире — вывод) дает движение
как формулу, здесь никакой линии нет, она заменена функциональной связью. Движение, понятое как
форма, есть континуум "одновременных точек", и логическая связь этих точек есть связь причастности,
но не причинности. Линия не может быть причиной своих точек, причиной своих атрибутов. Движение,
понятое как формула, воспроизводится чисто аналитически, связь алгебраических знаков (то есть
функциональная связь) — это формально-логический эквивалент "причинной логики".
Далее. Движение, понятое как форма, "витает в воздухе", носит "вне-положный" исследователю,
образный характер. Вне-положный — для геометрической "интуиции". Движение, понятое
(представленное в теории) как формула, есть имманентное исследователю движение мысли (вывода,
доказательства). Антиномия возрождается. Но так и должно быть — ведь в действиях математика
должен быть воспроизведен в его идеализованных определениях классический объект.
Только сейчас, продумав то аннигилирующее сопряжение двух континуумов и двух атомистик
(физической и математической) и двух логик бытия, которое впервые возникло в "сквозном
эксперименте" Галилея, возможно вернуться к галилеевским "монстрам", понять их действительный
логический смысл. Понять их смысл как исходных начал, исходных "спор разума" Нового времени.
Понять их смысл как неделимых логических атомов мысли.
Дело в том, что те два континуума, о которых я сейчас детально говорил, все же не порождаются прямо
в сквозном эксперименте "Диалога..." (в "предельном переходе"). Нет, это только внутри "Бесед..."
заново рожденный мир Коперника рождается (и расщепляется) вторично — в особом, собственно
логическом, элементарном действии, в тех самых маргинальных курьезах и головоломках,
первоначальное определение которых было введено выше.
6. Снова "монстры" и головоломки. Единый определяющий эксперимент Галилея
Можно сразу же сказать так: в Галилеевых "монстрах" и головоломках осуществляется некий
"определяющий эксперимент" (эксперимент, определяющий формирование исходных логических схем
мышления Нового времени). Этот "определяющий — новые начала разума
104
— эксперимент" следует
отличать от того "сквозного эксперимента" "Диалога..." — "Бесед...", о котором мы рассуждали до сих
пор.
В "сквозном эксперименте" происходил "предельный" переход мира (и логики) Аристотеля в мир (и
логику) Галилея. Сейчас речь пойдет о тех экспериментах, которые направлены уже на этот
сформированный Галилеем идеальный мир — в попытках понять его "до конца", в попытках его
самообосновать. Теперь эксперимент осуществляется уже не над аристотелевским миром, но в глубинах
мира галилеевского, по отношению к основным' элементам движения этого мира, чтобы вскрыть их
логическую всеобщность.
"Определяющий эксперимент" Галилея и все его основные схемы — "монстры", головоломки,
парадоксы — занимают в тексте "Бесед..." вполне определенное и четко ограниченное место. Это —
День Первый — первые двадцать пять страниц. Введены схемы-головоломки в следующем контексте.
В предисловии "Читателям от издателей" Галилей пишет: "...автор открыл две новых науки и доказал
убедительно, то есть геометрически, их принципы и основания... одна из наук касается предмета
вечного, имеющего первенствующее значение в природе, обсуждавшегося великими философами и о
котором уже написано множество томов, короче сказать, движения падающих тел... Другая наука, также
развитая из основных ее принципов, касается сопротивления, оказываемого твердыми телами при
стремлении их сломить... познания такого рода весьма полезны в науке и искусстве механики" (7/114).
Две эти "новые науки" — наука о движении падающих (в пустоте) тел и наука о сопротивлении твердых
тел разрушению (удару, давлению) — доказаны Галилеем, исходя из единых принципов — принципов
геометрии. "...Вся механика имеет своею основою геометрию; и мы знаем, что круги, треугольники, а
также цилиндры, конусы и другие формы твердых тел не только отличаются друг от друга большей или
меньшей величиной, но и изменяются одни по одним, а другие по другим законам" (77117).
Однако геометрия эта, положенная в основание двух новых наук, — геометрия весьма странная: ее
законы и ее фигуры нельзя встретить ни в каких учебниках, ни в каких геометрических теориях. Это
столь же геометрия, сколь и механика, точнее — это ни то, ни другое, но нечто весьма полезное для
понимания связи того и другого, для механического обоснования новой геометрии и геометрического
обоснования новой механики.
Странность этой Галилеевой геометрии выясняется сразу же, как только обнаруживается, что
"придуманные" Галилеем геометрические фигуры и преобразования долженствуют разом, заодно
решить ключевые проблемы обеих наук: науки о падении тел в пустоте и науки о сопротивлении тел
разрушению. Новое ("странное") понимание движения, новое двусмысленное "понятие движения" —
вот корень всех геометрических странностей.
Начинается все с постановки одной из частных задач "второй великой науки" — науки о сопротивлении
тел. Возникает вопрос о возможной роли внутренних пустот в твердых телах для возрастания
сопротивления этих тел внешнему разрушению. Сальвиати высказывает предположение: "Кто знает, не
действуют ли в мельчайших частях (тел. — В.Б.) также и мельчайшие пустоты, и не они ли держат в
связном состоянии части твердого тела, подобно тому как отдельные моменты образуют совокупность?
Скажу вам то, что сейчас пришло мне в голову; выдаю это не за окончательную истину, но за домысел,
связанный с немалыми затруднениями и требующий исследования. Посмотрите, не найдете ли вы тут
чего-нибудь, что вам понравится; об остальном судите, как вздумается" (77130 — 131).
Итак, все дальнейшее лишь "домыслы", "требующие дальнейшего исследования", головоломки и
парадоксы, придуманные для того, чтобы резче выявить суть проблемы, и не претендующие на
научную строгость и истинность. Это, как говорит Галилей в другом месте, "уклонения", не связанные
"строгим и жестким методом", "не стоящие в необходимой связи с поставленной... задачей..." (77121).
Для доказательства (или демонстрации) своего предположения, что пустоты в мельчайших частях
твердых тел определяют связность тел и их сопротивление разрушению, Галилей предлагает
своеобразный, вновь уклоняющийся в сторону мысленный эксперимент:
"Сальвиати. Раз мы уже дошли до парадоксов, то попробуем,

нельзя ли каким-либо образом доказать, что в некоторой конечной непрерывной величине может
существовать бесконечное множество пустот" (//132).
Итак, сам Сальвиати (Галилей) определяет все последующее как парадокс. И как мы убедимся, это
парадокс в достаточно строгом смысле слова — некое логическое противоречие, отличающееся от
антиномии.
Но вернемся к "монстрам" Галилея.
Сейчас перед нами появится первый "монстр" (и эксперименты с ним) — центральный для понимания
галилеевских логических фигур и далеко уводящий от первоначальной частичной задачи, точнее,
уводящий в глубь этой же самой задачи (рис. 2).
"...Необходимо рассмотреть одно предложение, не связанное с другими, но от которого зависит
решение данного вопроса, а последнее приведет... ко многим новым и удивительным понятиям. Для
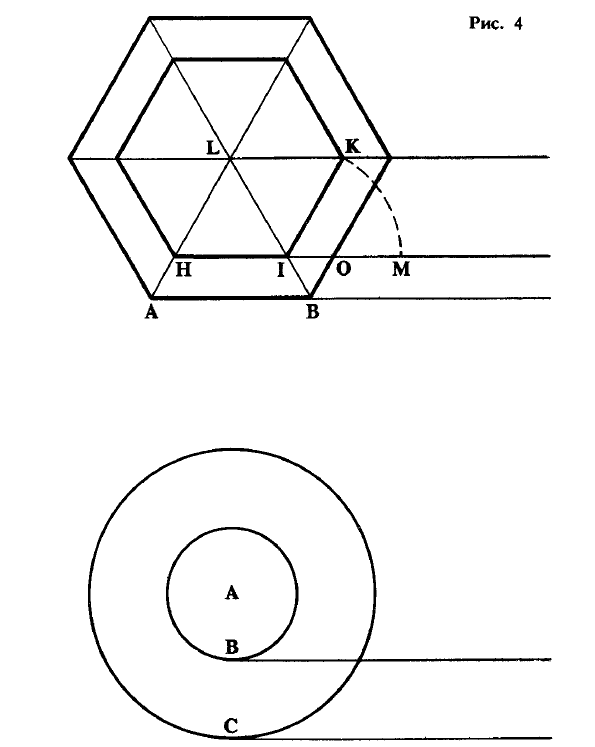
пояснения начертим аккуратно следующую фигуру. Дан равносторонний и равноугольный
многоугольник с любым числом сторон, центром которого является точка G; предположим, что это
будет шестиугольник ABCDEF. Впишем в него подобный же, но меньший концентрический
многоугольник HIKZMN. Продолжим одну из сторон АВ большего многоугольника в направлении S, в
соответствии с чем продолжим в том же самом направлении в сторону меньшего шестиугольника HI,
так что линии НТ и AS будут параллельными... Проделав это построение, представим себе, что больший
многоугольник катится по линии AS, увлекая с собою и меньший многоугольник. Ясно, что при начале
движения В конечная точка стороны АВ останется на месте, точка А поднимется, а точка С опустится,
описав дугу CQ... Если продолжать катить многоугольник и сделать второй поворот, то сторона DC
большего многоугольника займет положение QX, сторона KL меньшего придет в YZ, перескочив
пространство PY, а центр, двигаясь все время над линией GV, достигнет последней в точке R, сделав
скачок CR. В результате полного оборота больший многоугольник отложит на линии AS подряд без
каких-либо промежутков шесть равных линий... меньший многоугольник также отложит шесть
отрезков, равных его сторонам, но разделенных пятью другими, хорды которых — части линии НТ —
остаются не затронутыми многоугольником; наконец, центр G прикоснется к линии GV только в шести
точках... пространство, пройденное малым многоугольником, почти равно пройденному большим...
если рассматривать линию НТ сполна, т.е. вместе с отрезками под дугами" (// 132 — 133).
(Так же будет и с качением любого, хоть тысячеугольного, многоугольника с вписанным в него
меньшим тысячеугольником.)
"Таким образом, когда больший многоугольник с тысячью сторон, постепенно вращаясь, пройдет
прямую линию, равную своему периметру, меньший многоугольник пройдет в то же самое время
приблизительно такой же путь, составленный из тысячи отрезков, равных его сторонам, и тысячи
пустых пространств между ними, как мы можем назвать эти промежутки, в противоположность
отрезкам, отмеченным наложением сторон многоугольника. В том, что было пока сказано, нет ничего
сомнительного или возбуждающего какие-либо затруднения. Но теперь скажите мне: если из какого-
либо центра, например из точки А, мы опишем две концентрические окружности, представим себе
круги связанными между собою... и покатим большой круг по линии BF... то что произойдет с меньшим
кругом и центром после того, как большой круг сделает полный оборот? Центр, конечно, пройдет всю
линию AD, а окружность малого круга своим прикосновением пройдет всю линию СЕ так же, как это
имело место ранее с малым многоугольником, с той только разницей, что линия НТ не во всех своих
частях затрагивалась периметром многоугольника и содержала столько же пустых промежутков,
сколько было отрезков, отмеченных наложением сторон многоугольника; что же касается кругов, то
окружность меньшего не может оторваться от линии СЕ так, чтобы не соприкасаться с нею в одной
точке, и всегда одна из точек окружности лежит на прямой. Каким же образом меньший круг может
пройти линию, настолько превышающую его окружность, без скачков и промежутков?" (//133 — 134).
После попыток Сагредо разрешить эту трудность, Сальвиати предлагает свое решение
(предположение): "...как в многоугольнике со ста тысячами сторон путь, пройденный при обороте,
измеряется обводом большего многоугольника, т.е. отложением без перерыва всех его сторон, в то
время как путь меньшего многоугольника также равен ста тысячам его сторон с прибавлением такого
же числа, т.е. ста тысяч пустых промежутков, так и в кругах (представляющих собою многоугольники с
бесконечно большим числом сторон) линия, образуемая непрерывным наложением бесконечно
большого числа сторон большего круга, приблизительно равна по длине линии, образованной
наложением бесконечно большого числа сторон меньшего круга, если включить в нее и промежутки; а
так как число сторон не ограничено, а бесконечно, то и число промежутков между ними также
бесконечно... Я хотел бы, чтобы вы заметили себе, что... представляя себе линию разделенной на
неконечные части, т.е. на бесконечно многие ее неделимые, мы можем мыслить ее колоссально
растянутой без вставки конечных пустых пространств, а путем вставки бесконечно многих неделимых
пустот. То, что я сказал о простых линиях, относится также и к поверхностям твердых тел, если
рассматривать их как состоящие из бесконечного множества атомов... Если допустить предельное...
разложение тела на лишенные величины и бесчисленные первичные составляющие, то можно
представить себе такие составляющие растянутыми на огромное пространство путем включения не
конечных пространств, а только бесконечно многих пустот, лишенных величины" (//135).
В этих размышлениях и предположениях Сальвиати заложена суть нового понимания движения,
воспроизведены основные логически неделимые атомы (схемы) мышления, характерные для Нового
времени, хотя изложены они в странной, необычной форме вне-логического построения "монстров".
Показать особое значение этой исходной головоломки помогает нам тот спор, который здесь
начинается между Сальвиати и Симпличио. Симпличио высказывает те коренные логические
возражения, отвечая на которые (строя новые парадоксальные "головоломки") Сальвиати дает цельный
сгусток новых "спор разума", коренящихся в логике-онтологии эксперимента.
"Симпличио.... В течение нашей беседы во мне родились многие сомнения, от которых я при всем
желании не могу освободиться. Прежде всего, следующее... каким образом линия AD, описанная
центром, составляющим одну точку, может быть приравнена к этому центру, в то время как состоит из
бесконечного числа точек? Кроме того, это составление линии из точек, делимого из неделимого,
конечного из неконечного кажется мне нелегко преодолимым препятствием; точно так же и признание
существования пустоты, столь решительно отвергаемой Аристотелем, представляет большие
затруднения" (7/136).
Значит, аристотелевские сомнения Симпличио сводятся к трем трудностям:
— тождество — в движении — линии и точки?
— формирование конечного (отрезка линии) из бесконечного, делимого из неделимых?
— пустота как основа строения "заполненного" тела и как основное условие движения?
Отвечая на эти сомнения, Сальвиати и набрасывает неявную (но полную) схему нового мышления. И то,
как он вводит свои рассуждения, показывает высокую степень логического осознания проблемы самим
Галилеем.
"Сальвиати. Такие затруднения действительно существуют... но вспомните о том, что мы имеем дело с
бесконечными и неделимыми, постичь которые нашим конечным умом невозможно... человеческая
речь не приспособлена для выражения таких понятий. Однако я все же позволю себе изложить
некоторые свои измышления, которые хотя и не исчерпывают вопроса, но могут представить... интерес
благодаря своей новизне" (II 136).
В своих "измышлениях" Сальвиати каждый раз формирует новый парадокс — устраняет исходную
несообразность, "указав другую подобную или еще большую, как иной раз удивительные вещи
бледнеют перед лицом чудесных" (III 37). Вот эти (основные) парадоксы, необходимые для
обоснования исходного парадокса "качения кругов".
В ответ на сомнение о возможности приравнять точку и прямую линию (не забудем, что все эти
трудности возникают в контексте эксперимента с качением вписанных кругов, а этот эксперимент
придуман для того, чтобы разрешить парадокс тождества пустоты и "заполненности") Сальвиати строит
новый мысленный "геометрический эксперимент", в котором две одинаковые поверхности и два
одинаковых тела, поставленные на эти поверхности как на основания, постепенно уменьшаются. В
итоге — одно тело вместе со своей поверхностью превращается в "предлинную" линию, а другое со
своей поверхностью — в точку.
Таким образом, в одном случае получается лишь одна-единственная точка, в другом — бесконечное
множество их.
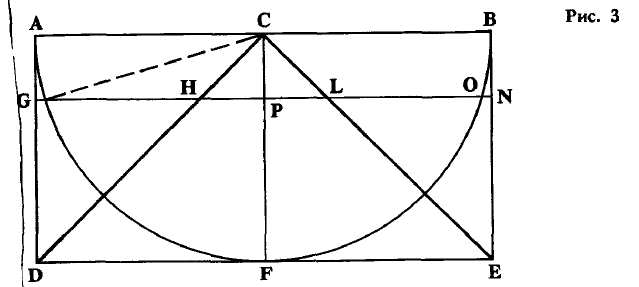
Строится чертеж (рис. 3): полукруг AFB с центром С и описанный около него прямоугольный
параллелограмм ADEB. От центра к точкам D и Е проведены прямые линии CD и СЕ. Вся фигура
вращается вокруг неподвижной линии СР. Прямоугольник опишет цилиндр, полукруг AFB — полушар,
а треугольник CDE — конус. Полушар вынимается, а оставляется конус и "чаша" — часть цилиндра,
выходящая за пределы полушара. Далее доказывается равновеликость чаши и конуса. Затем сечем обе
фигуры плоскостью, параллельной основанию. Плоскость эта, где бы ее ни провести, всегда отсекает
два равных между собой тела — верхушку конуса и верхнюю часть чаши. Также остаются равными
основания этих тел — упомянутая полоса и круг HL. Проводя секущую плоскость все выше и выше, мы
все время получаем равные тела и основания. И наконец, в последний момент (в вершине) большая
окружность оказывается равной одной точке. В этот момент оба тела (всегда равные) и обе площади
(всегда равные) перейдут — одно в окружность, другое — в точку, которые равны между собой. "...Если
бы чаша была такой вместимости, как небесный свод, то остаток ее верхнего отрезка и вершина
находящегося в ней конуса всегда оставались бы равновеликими, хотя бы и превратились в конце
концов первое тело — в необъятный большой круг небесного свода, а второе — в простую точку" (II
137 — 138).
Заметим: движение секущей плоскости вверх по равновеликим телам (уменьшение этих тел) сохраняет
их равновеликость и приводит — "в последний момент", "в конце концов", "в вершине конуса" — к
приравниванию "необъятного круга" и точки.
Таким парадоксальным экспериментом отвечает Сальвиати на первое сомнение Симпличио.
Возражение это не устраняет странность и невозможность предположений о равенстве "линии" и
"точки", но демонстрирует процесс (логически необходимый процесс) возникновения — в "последний
момента — этой логической несуразности. Именно такая ситуация — логически необходимое движение,
оканчивающееся — в пределе — трансформацией исходных логических утверждений, и есть
"парадокс" в собственном смысле слова в отличие от "антиномии", основанной на параллелизме двух
взаимоисключающих определений (или двух цепочек определения) одного логического субъекта.
Затем, отвечая на второе сомнение Симпличио относительно возможности построить конечное из
бесконечных, делимое из неделимых, Сальвиати формулирует новые парадоксы, изобретает новые
"монстры" и головоломки.
Но сначала он подчеркивает исходную парадоксальность этой задачи. Тройную парадоксальность.
Во-первых, само решение вопроса о бесконечном или неделимом не под силу человеческому конечному
разуму. Необходимо как-то осмыслить (представить возможной) эту невозможность — освоить
бесконечность мира в конечном человеческом разумении. Во-вторых, возникает "вторая производная"
этой трудности — уже не в гносеологическом, но в логическом плане: необходимо осмыслить
построение конечного (предмета, линии...) из бесконечных, далее неделимых (?) единиц. В-третьих,
необходимо соединить в одном решении две — и по одиночке неразрешимые — задачи: "изучать
одновременно и бесконечное и неделимое" (Я 139).
Однако именно сопряжение всех этих трудностей, их одновременное решение лежит в основе
предлагаемых Сальвиати головоломок.
Чтобы обосновать введение этих головоломок, Сальвиати прежде всего показывает некорректность
самой симпличиовской постановки вопроса.
Сальвиати ставит под вопрос само понятие "составить", "построить". Да, составить конечное из
бесконечных частей, образовать делимое из неделимых невозможно. Этот процесс бесконечен, в нем
мы все больше приближаемся к целому, но никогда его не достигнем. Но по способу бытия (а не
формирования) конечное н делимое есть целостное, неделимое, бесконечное (?). И в этом смысле к
конечному, понятому как бесконечное, к делимому, понятому как неделимое, неприменимы те обычные
понятия, которые мы употребляем по отношению к конечным и делимым вещам, линиям, плоскостям.
"...Такие свойства, как большая или меньшая величина и равенство, неприменимы к бесконечному..." (Я
140). Поэтому бессмысленно и сомнение Симпличио в том, что (в случае признания бесконечности
конечных линий) одна бесконечность (точек меньшей линии) будет меньше другой бесконечности
(точек, составляющих большую линию).
"...Когда синьор Симпличио предлагает мне неравные линии и спрашивает меня, как может быть, чтобы
в большей из них не содержалось большего количества точек, чем в меньшей, то я отвечаю ему, что их
там не больше, не меньше и не одинаковое количество, но бесконечное множество в каждой". Это —
равномощные, хотя и иные бесконечности, иные неделимые. "В самом деле, если бы я ответил, что
число точек одной линии равняется числу квадратных чисел, в другой — большей — их содержится
столько, сколько существует чисел вообще, а в какой-нибудь меньшей столько, сколько существует
кубов, то был ли бы удовлетворительным мой ответ, приписывающий линиям разное число точек,
являющееся в то же самое время в каждом случае бесконечным?" (//141).
Здесь обычно проводится параллель между этим утверждением Сальвиати (Галилея) и учением Кантора
об "актуальных множествах". Но Галилей в логическом плане смелее Кантора. Он переформулирует
(снимает) собственное утверждение. Для него в ограниченном континууме (данной линии, к примеру)
не актуальное и не потенциальное бесконечное множество (точек), но — неопределенное. Строго
говоря, к ограниченному континууму неприменимо не только понятие "больше", "меньше", "равно"; к
нему неприменимо ни понятие "конечно", ни понятие "бесконечно".
"...На предложенный... вопрос, конечно или бесконечно количество частей континуума, самым
правильным было бы ответить: оно не конечно и не бесконечно численно, но соответствует любому
данному числу..." (II 143). При таком рассуждении бессмысленно также различение между
"актуальным" и "потенциальным" разделением этого континуума на части. Приобретает значение нечто
иное: форма (идея) определения этого ограниченного континуума в его самоограничении — как
фигуры, или как формулы, или как алгоритма — и тем самым определение способа его отождествления
с тем или иным, пусть бесконечным, числом.
Только после всех этих уточнений и углублений проблемы Сальвиати возвращается к исходному
сомнению Симпличио, но уже в новой редакции: необходимо (но возможно ли?) понять конечное и
делимое как бесконечное и неделимое. Такое понимание никак не может быть отождествлено с
бесконечным делением, разложением какой-то линии или фигуры. "Тот, кто, желая разложить линию на
бесконечное множество ее точек, предполагает достигнуть своей цели тем же путем, каким пользуются
другие для разделения линии на сорок, шестьдесят или сто частей, т.е. сперва делит ее пополам, затем
на четыре части и так далее, и надеется получить, таким образом, бесчисленное множество точек, грубо
ошибается, потому что такой процесс постепенного деления конечных величин необходимо было бы
продолжать вечно; достигнуть же таким путем приближения к неделимым в конечный период времени
совершенно невозможно. Я полагаю даже, что, продолжая деление и умножая число частей в
предположении приблизиться к бесконечности, мы на самом деле удаляемся от нее..." (Л144 — 145).
Здесь вводится парадокс, демонстрирующий, какими свойствами должен обладать континуум как
единица, как нечто кратное только самому себе и, следовательно, неделимое.
"Сальвиати.... Если какое-либо число должно являться бесконечностью, то этим числом должна быть
единица; в самом деле, в ней мы находим условия и необходимые признаки, которым должно
удовлетворять бесконечно большое число, поскольку она содержит в себе столько же квадратов,
сколько кубов и сколько чисел вообще.
Симпличио. Я не совсем постигаю, как следует понимать сказанное вами.
Сальвиати. Сказанное не заключает в себе ничего сомнительного, так как единица является и
квадратом, и кубом, и квадратом квадрата и т.д., точно так же квадраты и кубы и т.д. не имеют никакой
существенной особенности, которая не принадлежала бы и единице, как, например, свойство двух
квадратных чисел постоянно иметь между собою среднее пропорциональное. Возьмите любое
квадратное число, с одной стороны, и единицу — с другой, и вы всегда найдете среднее
пропорциональное число... Отсюда заключаем, что нет другого бесконечного числа, кроме единицы".
(Единица, экстенсивно составляя элемент бесконечного ряда, интенсивно воплощает все определения
бесконечности, все возможные арифметические операции (умножения, деления, возведения в степень,
пропорциональности).) "Это представляется столь удивительным, что превосходит способность нашего
представления, но в то же время поучает нас, сколь заблуждается тот, кто желает наделить бесконечное
теми же атрибутами, которые присущи вещам конечным, в то время как эти две области по природе
своей не имеют между собою ничего общего" (П 145).
Теперь (только теперь), выяснив континуальность единицы, возможно понять отличие континуальности
бытия и континуальности измерения, определения бесконечности и движения к пределу.
Сальвиати предлагает Симпличио "фокус", в котором он сможет свести деление континуума на
бесконечное число неделимых частей "к такому же короткому процессу, как тот, который требуется
другим для разделения линии на сорок частей..." (П 144).
Симпличио принимает это замечание за веселую шутку. Тогда Сальвиати, выдвинув единственное
условие ("...не надо требовать, чтобы он отделил одну точку от другой и показал их отдельно на
бумаге"), начинает свой "эксперимент".
"...Сгибание линии под углами так, чтобы образовался квадрат, или восьмиугольник, или
многоугольник с сорока, ста или тысячью сторон, представляется вам достаточным для
действительного выявления тех четырех, восьми, сорока, ста или тысячи частей, которые, как вы
говорите, содержались потенциально в первоначальной прямой линии, то, когда я образую из прямой
линии многоугольник с бесконечным числом сторон, т.е. когда я сгибаю ее в окружность, не
могу ли я с таким же правом утверждать, что я вызываю к действительности то бесконечное множество
частей, которое первоначально, пока линия была прямой, содержалось в ней, по вашему утверждению, в
потенции?"
Только "последнее... крайнее деление должно разложить делимое на бесконечное множество
неделимых, чего... мы не можем достигнуть последовательным раздроблением на большее и большее
количество частей. Предложенный же мною метод... разделять бесконечность одним разом... должен...
заставить принять, что континуум состоит из абсолютно неделимых атомов. Этим дается также путь...
чтобы выбраться из сложного лабиринта разных вопросов, к которым принадлежит, например,
затронутый уже нами вопрос о связности частей твердого тела; приняв, что тела состоят из неделимых
частиц, мы можем... понять и явления разрежения и сгущения тел, не прибегая для объяснения первого
к признанию пустых промежутков, а второго — к проникновению одних тел в другие" (И 153 — 154).
Круг замыкается. Мы возвращаемся к исходной трудности и к исходному парадоксу с "качением
кругов".
(Во время качения и большой и вписанный в него малый круг осуществляют как поступательные, так и
обратные движения по линиям своего вращения: см. рис. 4. Здесь, как мы знаем, происходит нечто
радикально отличное от качения двух — вписанных друг в друга — многоугольников...) "В результате
бесконечное множество неделимых сторон ("точек. — В.Б.) большего круга со своим бесконечным
множеством неделимых обратных движений, совершаемых во время бесконечно кратких остановок
бесконечно большого числа сторон меньшего круга, и с бесконечным множеством продвижений вперед,
равных бесконечному числу сторон меньшего круга, описывает линию, равную описываемой меньшим
кругом и содержащую бесконечное множество бесконечно малых наложений, образующих утолщение
или, лучше сказать, уплотнение без проникновения одних конечных частей в другие, чего нельзя
сделать с разделенной на конечные части линией, равной периметру какого-либо многоугольника;
выпрямленный, он не может сократиться без того, чтобы стороны его частью не налегли одна на другую
или не проникли одна в другую. Такое уплотнение бесконечного множества бесконечно малых частиц
без взаимного проникновения конечных частей и расхождение бесконечного множества бесконечно
малых частиц с образованием неделимых пустот представляют собою все, что можно сказать об
уплотнении и разрежении тел, не прибегая к допущению взаимного проникновения частей тела или к
образованию пустот конечной величины. Если это вам нравится, то примите мои выводы; если же нет,
то считайте их ложными... Я только напомню вам при этом два слова: мы находимся в области
бесконечных и неделимых" (7/156).
Таким образом, "для понимания разрежения необходимо воспользоваться линией, описываемой малым
кругом при вращении большого круга, которая оказалась больше, чем окружность этого малого круга;
для понимания же сгущения мы покажем, как при вращении малого круга больший круг описывает
прямую линию, меньшую по длине, чем его окружность..." (II \ 54).
В этот момент Симпличио и формулирует свое основное возражение: "Ваши рассуждения и
доказательства суть чисто математические, отвлеченные и оторванные от всякой ощущаемой материи: я
полагаю, что по отношению к физической материи и предметам, встречающимся в природе,
выведенные законы не могут иметь приложения" (II 157).
Продумаем теперь заново весь сгусток парадоксов и "монстров", изобретенных Галилеем на этих
страницах, и тогда окончательно ответим на сомнения Симпличио.
7. Определяющий эксперимент Галилея и механика Нового времени
Все парадоксы Галилея, все его "монстры" есть разветвление и конкретизация единого, единственного
парадокса (эксперимента) — "качения двух концентрических кругов" — в соотнесении с "качением
двух концентрических бесконечноугольных многоугольников".
И в контексте этого единого, даже не мысленного, а просто вымышленного эксперимента оформляется
начало мышления Нового времени.
В этом контексте осуществляется порождение и взаимоопределение ("дополнительность") двух
континуумов — математического и физического. Симпличио даже не подозревает, как он прав,
утверждая, что рассуждения Сальвиати "чисто математические" и что они исключают "физическую
реальность". Но — ив этом неправота Симпличио — эти рассуждения предполагают не только
исключение физической реальности, они предполагают логическое обоснование этой реальности и
исключение "континуальности (и атомистики) математической". В "качении кругов" осмысливается
парадокс такого доведения до предела физического континуума, в котором он переходит в определения
континуума математического и обратно... Сопряжение "двух великих новых наук" — • "науки о падении
тел" и "науки о сопротивлении тел внешнему разрушению" — позволяет рассмотреть проблему
строения вещей и проблему движения предметов как одну и ту же (по происхождению) проблему.
Абсолютная заполненность предметов (точки принимаются как стороны бесконечноугольных
многоугольников) тождественна в головоломке Галилея абсолютной пустоте (точки понимаются как
промежутки-скачки, никаких пространственных определений не имеющие). Пустота здесь создается не
путем мысленного разрежения среды от сопротивляющегося воздуха, трения и т.д. (как в собственно
механических мысленных экспериментах), но путем чисто логического отождествления
"непрерывности" и "скачков", бесконечно делимых пространств и "неделимых пустот". В таком
эксперименте одно определение понимается и делается возможным за счет исключения и
предположения другого — противоположного. Здесь не нужно освобождать среду для движения, здесь
само движение (наших головоломных кругов, понимаемых — и не понимаемых — как
бесконечноугольные многоугольники) определяет и свою собственную возможность, и свою
невозможность.

В апориях Зенона — Аристотеля
105
определения чистой возможности (потенции) движения (до его
начала и после его окончания, в идее "возможных перемещений плеч рычага") и определения
невозможности бытия движения были противопоставлены друг другу. В "монстрах" Галилея эти
определения соединяются в одном — обреченном антиномически разделиться — определении. Но об
антиномическом разделении этих определений — дальше. Сейчас существенно подчеркнуть, что в
головоломках Галилея определения движения уже не носят априорного характера ("понять движение
означает понять его как нечто непонятное, нечто извечно подлежащее пониманию как предмет
понимания, внеположный мысли").
Они не носят в этих головоломках еще и антиномического характера ("понять движение означает
понять его в двух взаимоисключающих, но "в себе" непротиворечивых теориях"). В головоломках
Галилея определения движения носят еще парадоксальный характер, т.е. характер изначального
самообоснования новой логики. Взятые раздельно, "энигмы" Галилея почти повторяют "загадки"
Кузанского или Бруно. Сопряженные вместе, они приобретают совсем иной смысл, возможный только в
XVII в.
В контексте исходного эксперимента с "качением кругов" заложены буквально все основные
механические эксперименты Нового времени, даны — в неделимом логическом атоме (точнее —
монаде) — основные идеализации классической механики, только представленные еще не как
фрагменты осуществления некоей уже наличной механистической стратегии, но как разные грани
обоснования самой возможности механического эксперимента. Больше того, исходный мысленный
эксперимент "Бесед..." формирует такое всеобщее понятие движения, в котором само движение
определяется как элементарный механический эксперимент.
Укажу сейчас лишь вкратце на основные определения "качения кругов" как "порождающей структуры"
(термин Н. Хомского
106
) механики и логики Нового времени.
а) Об одном я уже сказал: в "качении кругов" исследована логика порождения пустоты как основы
исследования инерции. Причем движение точки ("угла бесконечноугольного многоугольника") в этой
пустоте, в этом процессе формирования пустоты носит абсолютно инерционный характер.
б) В своем движении по параллельным линиям два вписанных круга, понятые как бесконечноугольные
многоугольники, полагают себя как бесконечные прямые линии. Тождественность бесконечно большой
окружности и бесконечной (разомкнутой в никуда) прямой достигается в "качении кругов" без
экстраполяции конечного в некую особую бесконечно большую окружность. Эта тождественность
обнаруживается в каждом, пусть бесконечно малом, круге, понятом как бесконечноугольный
многоугольник, если представить движение этого "многоугольника" по прямой линии. К тому же в
движении двух концентрических окружностей обнаруживается также тождество замкнутой (цельной) и
разомкнутой, неопределенной, бесконечной (в смысле идущей в бесконечность) величины;
равномощность двух неравных окружностей, двух неравных (если оставаться в пределах понятия о
конечном) линий. В контексте чисто логического эксперимента нет нужды в том астрономическом,
сквозном эксперименте, в котором, как мы помним, мир Аристотеля превращался в мир Коперника.
Конечное, бесконечно малое, бесконечно большое находят свое исходное, еще не расчлененное
единство (тождество) в дифференциальном образе движения, в определении данной точки движения
как "неделимой пустоты"; как мгновенного определения круга ("в отличие" от многоугольника,
который обладал бы нескончаемо большим, но определенным числом углов и сторон); как "конечной
величины" (сторона "бесконечноугольного многоугольника"). И т.д. и т.п.
в) В этом эксперименте, в частности в его конкретизации через идею мгновенного формирования
"бесконечноугольного многоугольника" (круга), порождается логическая схема известных
экспериментов с падением тел.
"Бесконечноугольный многоугольник" (круг) Галилея, взятый в его двойном определении —
бесконечного движения к пределу, мгновенного выявления достигнутой бесконечности (линия
сгибается в окружность), — может быть понят как логический прообраз "падения" и "прикосновения",
кинематической картины движения "в "промежутке" и динамической картины удара, соприкосновения
