Bhattacharya R., Majumdar M. Random Dynamical Systems: Theory and Applications

Подождите немного. Документ загружается.

1.7 The Quadratic Family 33

orbits according to the Sarkovskii ordering. A period-three orbit appears

for the ﬁrst time when θ exceeds a critical value θ

∗

≈ 3.8284 so that, for

θ>θ

∗

, F

has a periodic orbit of every period. If a new periodic orbit

appears for the ﬁrst time after θ = θ

, say, then there exists an interval

(θ

,θ

] such that this new periodic orbit {x

(θ), x

(θ),...,x

(θ)},say,

remains (locally) attracting or stable. For θ>θ

this orbit becomes re-

pelling or unstable, as do all previously arising periodic orbits and ﬁxed

points. There are uncountably many points θ for which F

has no locally

attracting periodic or ﬁxed points. Indeed, while we do not develop the

range of formal deﬁnitions capturing chaos or complexity, we note that

the set of values of θ for which F

is chaotic has positive Lebesgue mea-

sure, according to the results of Misiurewicz (1983) and Jakobson (1981)

(see Theorem 7.1 for a particular case and Complements and Details).

For each θ ∈ A, α

has exactly one critical point (i.e., a point

where α



(x) = 0, and this critical point (z

∗

= 0.5) is independent of the

parameter θ.

1.7.1 Stable Periodic Orbits

Even though there may be an inﬁnite number of periodic orbits for a

given dynamical system (as in the Li–Yorke theorem), a striking result

due to Julia and Singer (see Singer 1978) informs us that there can be at

most one (locally) stable periodic orbit.

Proposition 7.1 Let S = [0, 1],A= [1, 4]; given some

θ ∈ A, deﬁne

(x) =

θ x(1 − x) for x ∈ S. Then there can be at most one stable peri-

odic orbit. Furthermore, if there is a stable periodic orbit, then w(0.5),

the limit set of z

∗

= 0.5, must coincide with this orbit.

Suppose, now, that we have a stable periodic orbit. This means that

the asymptotic behavior (limit sets) of trajectories from all initial states

“near” this periodic orbit must coincide with the periodic orbit. But what

about the asymptotic behavior of trajectories from other initial states? If

one is interested in the behavior of a “typical” trajectory, a remarkable

result, due to Misiurewicz (1983), settles this question.

Proposition 7.2 Let S = [0, 1], A = [1, 4]; given some

θ ∈ A, deﬁne

(x) =

θ x(1 − x) for x ∈ S. Suppose there is a stable periodic orbit.

Then for (Lebesgue) almost every x ∈ [0, 1], w(x) coincides with this

orbit.

34 Dynamical Systems

Combining these two results, we have the following scenario. Suppose

we do have a stable periodic orbit. Then there are no other stable periodic

orbits. Furthermore, the (unique) stable periodic orbit “attracts” the tra-

jectories from almost every initial state. Thus we can make the qualitative

prediction that the asymptotic behavior of the “typical” trajectory will

be just like the given stable periodic orbit.

It is important to note that the above scenario (existence of a stable

periodic orbit) is by no means inconsistent with condition (3.1) of the

Li–Yorke theorem (and hence with its implications). Let us elaborate

on this point following Devaney (1986) and Day and Pianigiani (1991).

Consider θ = 3.839, and for this θ, simply write α(x) = θ x(1 − x) for

x ∈ S. Choosing x

∗

= 0.1498, it can be checked then that there is 0 <

ε<0.0001 such that α

(x) maps the interval U ≡ [x

∗

− ε, x

∗

+ ε] into

itself, and |[α

(x)]



| < 1 for all x ∈ U . Hence, there is



x ∈ U such that

(



x) =



x, and |[α

(



x)]



| < 1. Thus,



x is a periodic point of period 3,

and it can be checked (by choice of the range of ε) that α

(



x) =



x <

α(



x) <α

(



x) so that condition (3.1) of Theorem 3.1 is satisﬁed. Also,



is a periodic point of period 3, which is stable, so that Proposition 7.2 is

also applicable. Then we may conclude that the set ℵ



of “chaotic” initial

states in Theorem 3.1 must be of Lebesgue measure zero. In other words,

Li–Yorke chaos exists but is not “observed” when θ = 3.839: the mere

existence of a set of initial conditions giving rise to complex trajectories

does not quite mean that the typical trajectory is “unpredictable.”

We note another formal deﬁnition of the concept of sensitive depen-

dence on initial conditions due to Guckenheimer (1979) that is of interest

in the context of the quadratic family. Let the state space S be a (non-

degenerate) closed interval and α be a continuous map from S into S.

The dynamical system (S,α) has Guckenheimer dependence if there are

a set T ⊂ S of positive Lebesgue measure and ε>0 such that given any

x ∈ T and every neighborhood U of x, there is y ∈ U and n ≥ 0 such

that |α

(x) − α

(y)| >ε. We note the following important result.

Proposition 7.3 Let S = [0, 1] and I = [1, 4]; given some

θ ∈ I con-

sider α

(x) =

θ x(1 − x),x ∈ S. Suppose there is a stable periodic orbit.

Then the dynamical system (S,α

) does not have Guckenheimer depen-

dence on initial conditions.

Finally, we state a special case of Jakobson’s theorem, which is a

landmark in the theory of chaos.

1.7 The Quadratic Family 35

Theorem 7.1 Let S = [0, 1],J= [3, 4], and α

(x) = θ x(1 − x) for

(x,θ) ∈ S × J . Then the set  ={θ ∈ J: (S,α

) has Guckenheimer

dependence} has positive Lebesgue measure.

For our purposes in later chapters the following proposition

sufﬁces.

Proposition 7.4 (a) Let 0 ≤ θ ≤ 1. Then F

(x) → 0 as n →∞, ∀x ∈

[0, 1]. (b) Let 1 <θ ≤ 3. Then F

(x) → p

≡ 1 − 1/θ as n →∞, ∀x ∈

(0, 1). (c) For 3 <θ ≤ 1 +

√

5,F

has an attracting period-two orbit.

Proof.

(a) Let 0 ≤ θ ≤ 1. Then, for every x ∈ [0, 1], 0 ≤ F

(x) ≤ x ≤ 1, so

that F

(x), n ≥ 1, is a nonincreasing sequence, which must converge to

some x

∗

. This limit is a ﬁxed point. But the only ﬁxed point of F

is 0.

Hence x

∗

= 0.

(b) First, consider the case 1 <θ ≤ 2. Then p

≤ 1/2, and x <

(x) < p

∀x ∈ (0, p

). Since F

is increasing on (0, p

) ⊂ (0, 1/2],

it follows that F

(x) < F

(x) < ···< p

. The increasing se-

quence F

(x) converges to a ﬁxed point x

∗

, which then must be p

Next let x ∈ ( p

, 1/2]. Here 1/2 ≥ x ≥ F

(x) ≥ p

and F

is increasing.

Hence, F

(x) ≥ F

(x) ≥···, that is, as n ↑∞, F

(x) ↓ y

∗

say y

∗

≥ p

. Again, by the uniqueness of the ﬁxed point of F

on [ p

, 1), y

∗

= p

.Forx ∈ [1/2, 1), y := F

(x) ∈ (0, 1/2], so that

(x) = F

n−1

(y) → p

Now consider the case 2 <θ ≤ 1 +

√

5. Then 1/2 < p

<θ/4 ≡

(1/2), and F

is decreasing on [1/2, θ/4]. Therefore, F

is in-

creasing on [1/2,θ/4], mapping this interval onto [F

(1/2), F

(1/2)].

Observe that the function θ → g(θ):= F

(1/2) ≡ (θ

/4)(1 − θ/4) is

strictly concave (i.e., g



(θ) < 0) on [2, 4] and g(2) = g(1 +

√

5) = 1/2,

implying that g(θ) > 1/2 for θ ∈ (2, 1 +

√

5). Applying F

repeatedly

to the inequality 1/2 ≤ F

(1/2), one gets 1/2 ≤ F

(1/2) < F

(1/2) <

(1/2) < ···, that is, F

(1/2) ↑ q

,sayasn ↑∞, implying q

(θ) is a ﬁxed point of F

∀θ ∈ (2, 1 +

√

5], with q

≤ p

(since 1/2 <

implies F

(1/2) < p

∀n). Similarly, applying F

to the inequal-

ity p

≤ F

(1/2) one gets p

≥ F

(1/2) ≥ F

(1/2), and repeatedly ap-

plying F

to the last inequality one arrives at F

(1/2) ≥ F

(1/2) ≥

(1/2) ≥···. Thus F

2n+1

(1/2) ↓ q

= q

(θ) ≥ p

as n ↑∞,

36 Dynamical Systems

∀θ ∈ (2, 1 +

√

5) (note that p

< F

(1/2) implies p

< F

(1/2))

∀n); in particular, q

is a ﬁxed point of F

Let 1/2 ≤ x ≤ p

, and 2 <θ≤ 3. Then, by the preceding arguments

(1/2) ≤ F

(x) ≤ p

≤ F

2n+1

(x) ≤ F

2n+1

(1/2), ∀n = 1, 2,....

Since F

has no periodic orbit of (prime) period 2 (i.e., F

has no

ﬁxed point other than p

on (0, 1)), one has q

= q

= p

. Hence

(x) → p

∀x ∈ [1/2, p

]. Deﬁne

= 1 −

≡ 1/θ . Then

1/2 and F

(

) = p

.On[

, 1/2], F

is increasing and, therefore, if

x ∈ (

, 1/2], then F

(x) ∈ ( p

, F

(1/2)], F

(x) ∈ [F

(1/2), p

) (since

is decreasing on [ p

, F

(1/2)]). Hence, ∀x ∈ [

, 1/2], with z :=

(x), one has F

(x) ≡ F

n−2

(z) → p

. Next, let x ∈ (0,

). Since F

is strictly increasing on (0,

] and x < F

(x), it follows that there is

a smallest integer k such that the sequence F

(x) increases as n in-

creases, n ≤ k − 1, and F

(x) ≥

(else, F

(x) ↑ x

∗

≤

, implying

the existence of a ﬁxed point x

∗

∈ (0,

]). Also, since F

k−1

(x) <

(x) ≤ p

, so that F

(x) ∈ [

, p

] and F

(x) ≡ F

n−k

(x)) → p

as n →∞. Similarly, if x ∈ ( p

, 1) there exists a smallest integer k such

that F

(x) ≥ p

(noting that F

is decreasing on ( p

, 1) and F

(x) < x

on ( p

, 1)). Hence F

(x) → p

. We have now shown that F

(x) → p

as n →∞, ∀x ∈ (0, 1).

√

5. Since F



) = 2 − θ<1, p

is a re-

pelling ﬁxed point, as is 0. For 1/2 < x < F

(1/2)(< p

) one then

gets F

(1/2) < F

(x) < F

2n+2

(1/2) < p

∀n. Therefore, F

(x) →

as n →∞. Similarly, for F

(1/2) < x < F

(1/2), F

2n+3

(1/2) <

(x) < F

2n+1

(1/2) ∀n, so that F

(x) → q

as n →∞. Since p

is repelling, it follows that q

> p

> q

, and {q

, q

} is an attracting

periodic orbit of F

Example 7.1 A Ricardian Model. Consider the model of a “Ricardian

system” discussed by Bhaduri and Harris (1987).

Suppose that the total product of “corn” (Y ) as a function of “labor”

(N )isgivenby

= α N

− bN

/2.

Hence, the average product of labor (AP

) is given by

= α −

1.7 The Quadratic Family 37

The “rent” R

in period t emerges as



−



“Proﬁt” P

is the residual after payment of rent and replacement of the

wage fund W

advanced to employ labor. Thus,

≡ Y

− R

− W

Bhaduri and Harris focus on the dynamics of the wage fund as represent-

ing the process of accumulation. The size of the wage fund governs the

amount of labor that can be employed on the land. At a given wage rate

w>0wehave

= wN

Accumulation of the wage fund comes from the reinvestment of proﬁts

accruing to the capitalists. If there is no consumption out of proﬁt income,

we have

t+1

− W

= P

This leads to

t+1

− N

−

− N

or upon simpliﬁcation

t+1

−

Since the positivity of the marginal product of labor requires a > bN

corresponding to all meaningful employment levels, Bhaduri and Harris

deﬁne n

≡ bN

/a < 1 and obtain

t+1

−

(1 − n

Thus, the basic equation governing the dynamics of the Ricardian sys-

tem is

t+1

= µn

(1 − n

where µ = a/w.

We can use the results on the quadratic family to study the emergence

of chaos in the Ricardian system.

38 Dynamical Systems

1.8 Comparative Statics and Dynamics

Samuelson’s inﬂuential monograph (Samuelson 1947, p. 351) empha-

sized the need to obtain results on comparative statics and dynamics: “the

usefulness of any theoretical structure lies in the light which it throws

upon the way economic variables will change when there is a change in

some datum or parameter.” In comparative statics, one investigates how

a stationary state responds to a change in a parameter explicitly affect-

ing the law of motion (see Proposition 8.1). Of particular interest is to

identify unambiguously the direction of change, and we shall see some

examples in the subsequent sections. The central notion of comparative

dynamics is to analyze the effects of a change in a parameter affecting

the law of motion on the behavior of the trajectories of the dynamical

system. Again, even for ‘simple’ nonlinear systems, a complete compar-

ative dynamic analysis is a formidable challenge, and we work out in

some detail several examples to stress this point.

To proceed more formally, consider a family of dynamical systems

(all sharing the same state space S) in which the law of motion depends

explicitly on a parameter θ:

t+1

= α

) (8.1)

where, for each admissible value of θ,α

is a map from S into itself. As

an example, take the quadratic family of maps:

t+1

= θ x

(1 − x

), (8.2)

where S = [0, 1] and θ ∈ [0, 4].

Now, with variations of θ we can pose the following questions:

(i) How do ﬁxed and periodic points behave in response to changes

in θ?

(ii) How does a change in θ affect the qualitative properties of the

various trajectories?

The ﬁrst question is at the core of bifurcation theory. We have seen that

even for simple families like (8.2), the number as well as local stability

properties of periodic points may change abruptly as the parameter θ

passes through threshold values. This point is elaborated in Section 1.8.1.

The second question leads to the issue of robustness of chaotic be-

havior, which can be precisely posed in alternative ways. First, one

can begin with a particular dynamical system (say, (2.3)) and show that

1.8 Comparative Statics and Dynamics 39

according to some formal deﬁnition, complicated behavior persists on

some nonnegligible set of initial conditions.

Next, one can proceed to look at the family of dynamical systems,

for example, (8.2) corresponding to different values of the parameter

θ, and try to assert that the class of parameter values giving rise to

complicated behavior from a non-negligible set of initial conditions is

itself non-negligible. (An example of this approach is Jakobson’s theorem

mentioned in Section 1.7.)

One can also take a topological approach to robustness. Consider

ﬁrst a given law of motion α for which the dynamical system (2.1) is

chaotic in some sense, and then vary α in an appropriate function space

and see whether chaos persists on a neighborhood containing α (recall

Proposition 3.1).

1.8.1 Bifurcation Theory

Bifurcation theory deals with the question of changes in the stationary

state of a dynamical system with respect to variations of a parameter

that affects the law of motion. We continue to introduce the main ideas

through some explicit computations.

Example 8.1 (continuation of Example 2.1) Consider a class of dy-

namical systems with a common state space S =

R and with the laws of

motion given by

(x) = x

+ θ, (8.3)

where “θ” (a real number) is a parameter. Our task is to study the im-

plications of changes in the parameter θ . The parallelism between the

dynamics of the family (8.3) and our earlier quadratic family (7.1) is

not an accident. But we do not take up the deeper issue of topological

conjugacy here (see Devaney 1986, Chapter 1.7 and Exercise 1, p. 47).

In order to understand stationary states, we have to explore the nature of

ﬁxed points of α

and its iterates α

. Consider ﬁrst the dependence of the

ﬁxed points of α

on the value of θ . The ﬁxed points of α

, for a given

value of θ, are obtained by solving the equation

(x) = x (8.4)

40 Dynamical Systems

and are given by

(θ) = (1 +

√

1 − 4θ )/2

−

(θ) = (1 −

√

1 − 4θ )/2. (8.5)

Observe that p

(θ) and p

−

(θ) are real if and only if 1 − 4θ ≥ 0or

θ ≤ 1/4. Thus, when θ>1/4, we see that the dynamical system (with

the state space S =

R) has no ﬁxed point. When θ = 1/4, we have

(

1/4

)

= p

−

(

1/4

)

= 1/2. (8.6)

Now when θ<1/4, both p

(θ) and p

−

(θ) are real and distinct (and

(θ) > p

−

(θ)).

Thus, as the parameter θ decreases through 1/4, the dynamical system

undergoes a bifurcation from the situation of no ﬁxed point to a unique

ﬁxed point at θ = 1/4 and then to a pair of ﬁxed points.

We turn to the “local” dynamics of the system from initial states close

to the ﬁxed point(s). Since α



(x) = 2x (does not depend on θ), we see that



1/4

(1/2) = 1 (so the ﬁxed point 1/2 is nonhyperbolic when θ = 1/4).

Now we see that



(θ)) = 1 +

√

1 − 4θ (8.7)



−

(θ)) = 1 −

√

1 − 4θ. (8.8)

For θ<1/4, α



(θ)) > 1 so that the ﬁxed point ( p

(θ)) is repelling.

Now consider p

−

(θ); of course, α



−

(θ)) = 1 when θ = 1/4. When

θ<1/4 but is sufﬁciently close to 1/4, α



−

(θ)) < 1, so that the ﬁxed

point p

−

(θ) is locally attracting. It will continue to be attracting as long

as |α



−

(θ))| < 1, i.e.,

−1 <α



−

(θ)) < 1

−1 < 1 −

√

1 − 4θ<1.

It follows that p

−

(θ) is locally stable for all θ satisfying

−3/4 <θ <1/4

when θ =−3/4, p

−

(θ) is again non-hyperbolic (i.e., |α



)|=1) and

for θ<−3/4, |α



−

(θ))| > 1 so that p

−

(θ), too, becomes repelling.

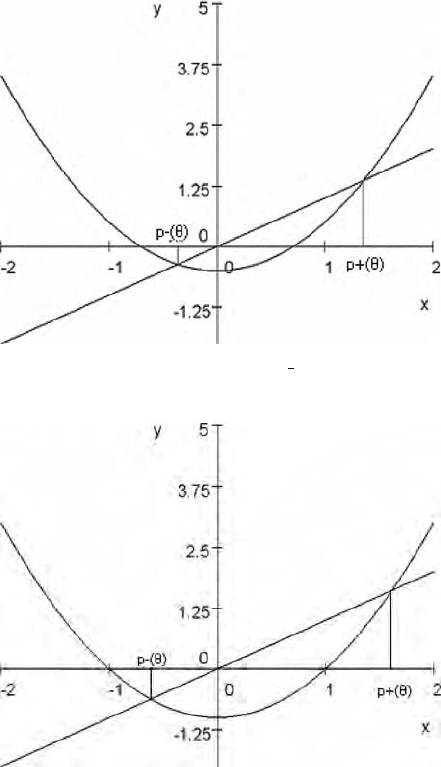
1.8 Comparative Statics and Dynamics 41

Figure 1.1a: θ =−

Figure 1.1b: θ =−1

Using a graphical analysis (see Figure 1.1) one can show the

following:

(i) For θ ≤ 1/4, if the initial state x > p

(θ)orx < −p

(θ), then

the trajectory from x tends to inﬁnity;

(ii) for −3/4 <θ<1/4, all the trajectories starting from x ∈

(−p

(θ), p

(θ)) tend to the attracting ﬁxed point p

−

(θ).

42 Dynamical Systems

Figure 1.1c: Second iterate of α(x ) = x

− 1

As the parameter θ decreases through −3/4, the ﬁxed point p

−

(θ)

loses its stability property; but more is true. We see a period-doubling

bifurcation: a pair of periodic points is “born.” To examine this, consider

the equation α

(x) = x, i.e.,

+ 2θ x

− x + θ

+ θ = 0 (8.9)

using the fact that both p

and p

−

are solutions to (8.2), we see that there

are two other roots given by

(θ) = (−1 +

√

−4θ − 3)/2 (8.10)

−

(θ) = (−1 −

√

−4θ − 3)/2. (8.11)

Clearly, q

(θ) and q

−

(θ) are real if and only if θ ≤−3/4.

Of course, when θ =−3/4, q

(θ) = q

−

(θ) =−1/2 = p

−

(θ). Fur-

thermore, for −5/4 <θ <−3/4, the periodic points are locally stable

(see Figures 1.1a–1.1c).

To summarize, we have conﬁrmed that

as the parameter passes through a “threshold” value, the number as

well as the local stability properties of ﬁxed and periodic points of a

family of dynamical systems may change.