Bhattacharya R., Majumdar M. Random Dynamical Systems: Theory and Applications

Подождите немного. Документ загружается.

4.6 Random Continued Fractions 323

We have shown that Corollary 5.2 of Chapter 3 applies with N = k,

˜χ = min{δ

,δ

} and z

as above.

Remark 5.2 Under the hypothesis of Theorem 5.2, {U

: n ≥ 0} con-

verges in distribution to a probability ¯π, irrespective of the initial vari-

ables U

, U

,...,U

k−1

. Also, it is asymptotically stationary, by Theorem

12.1 of Chapter 2.

Remark 5.3 The assumption of continuity of f in Theorem 5.2 may be

relaxed to that of measurability, provided f is monotone nondecreasing.

See Complements and Details, Chapter 3, Theorem C5.1.

4.6 Random Continued Fractions

In this section of the chapter we consider an interesting class of random

dynamical systems on the state space S = (0, ∞), deﬁned by

n+1

= Z

n+1

(n ≥ 0), (6.1)

where {Z

: n ≥ 1} are i.i.d. nonnegative random variables independent

of an initial X

. One may express X

as X

= α

···α

, where the

i.i.d. monotone decreasing maps on S into S are deﬁned by

x = Z

x ∈ (0, ∞)(n ≥ 0). (6.2)

Thus, writing [x; y] for x + 1/y,[z; x, y] = z + 1/[x; y], etc.,

= Z

= [Z

; X

= Z

= [Z

; Z

, X

= Z

= [Z

; Z

, Z

, X

],...,

= [Z

; Z

n−1

, Z

n−2

,...,Z

, X

], (n ≥ 1). (6.3)

In this notation, the backward iterates Y

= α

···α

maybeex-

pressed as

324 Random Dynamical Systems: Special Structures

= X

= α

= Z

= [Z

; X

= α

=[Z

; Z

, X

],...,Y

=[Z

; Z

,...,Z

, X

], (n ≥ 1). (6.4)

These are general continued fraction expansions as we will describe in

Subsection 4.6.1.

One may think of (6.1) as a model of growth, which reverses when the

threshold x = 1 is crossed, ﬂuctuating wildly between small and large

values.

4.6.1 Continued Fractions: Euclid’s Algorithm and the Dynamical

System of Gauss

There is a general way of expressing fractions by successively computing

the integer part of the reciprocal of the preceding fractional part. If the

process stops in four steps, for example, then one has

x =

. (6.5)

This is referred to as Euclid’s algorithm for reducing a rational number,

say, c/d to its simplest form p/q where p and q have no common factor

other than 1. For example, noting that 231/132 = 1 + 99/132, 132/99 =

1 + 33/99 = 1 + 1/3, we have

132

231

1 +

= [1, 1, 3].

In general, if x is rational, then one has a ﬁnite continued fraction expan-

sion. If x is irrational, the process does not terminate, and one has the

inﬁnite continued fraction expansion

x = [a

, a

,...,a

,...] =

...

. (6.6)

Here x = lim

n→∞

where p

= [a

, a

,...,a

] is called the

nth convergent, with p

and q

being relatively prime positive integers.

4.6 Random Continued Fractions 325

The process of computing the successive convergents may be de-

scribed in terms of the dynamical system on I = [0, 1) given by

T (x):=



− [

]ifx = 0,

0ifx = 0,

where [y] denotes the integer

partofy. (6.7)

For any x ∈ I , x = 0, if we put x

= x and x

= T

x for n ≥ 1, then the

continued fraction expansion (6.6) is given in terms of x

≡ T

x (n ≥ 0)





, a





,...,a





,... (6.8)

with the convention that the process terminates at the nth step if x

= 0.

In a famous discovery sometime around 1812, Gauss showed that the

dynamical system (6.7) has an invariant probability measure with density

g and distribution function G given by

g(y) =

(log 2)(1 + y)

, G(y) =

log(1 + y)

log 2

, 0 < y < 1, (6.9)

and that

(y):= m({x ∈ I : T

x ≤ y}) →G(y)asn →∞,0< y < 1,

(6.10)

where m is the Lebesgue measure on I = [0, 1). Since one may think

of a dynamical system as a Markov process with a degenerate transition

probability, which in the present case is p(x, {Tx}) = 1 ∀x ∈ I , (6.10)

says that if X

has distribution m on I (i.e., the uniform distribution

on I ) then the (Markov) process X

:= T

converges in distribution

to the invariant distribution (6.9), as n →∞.IfX

has the invariant

distribution g(y)dy, then X

= T

(n ≥ 1) is a stationary process.

Proofs of (6.10), and that of the fact that the dynamical system deﬁned

by (6.7) has inﬁnitely many periodic orbits, may be found in Khinchin

(1964) and Billingsley (1965).

4.6.2 General Continued Fractions and Random

Continued Fractions

For our purposes, we will consider general continued fractions deﬁned

as follows. Given any sequence of numbers a

≥ 0, and a

> 0(i ≥ 1),

one may formally deﬁne the sequence of “convergents” p

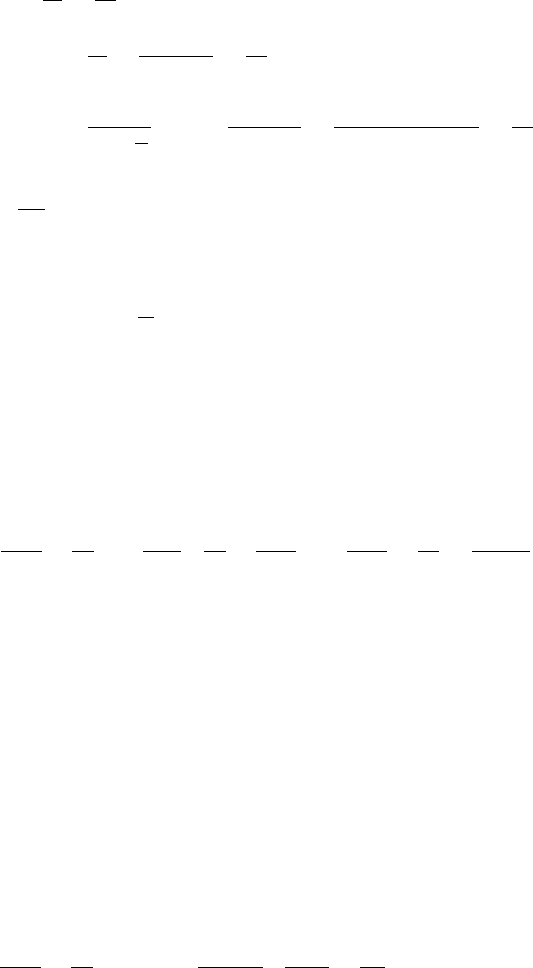
326 Random Dynamical Systems: Special Structures

= a

+ 1

, (6.11)

= a

+ 1

+ a

+ 1

In general, one uses the fact [a

; a

, a

,...,a

n+1

] = [a

; a

, a

,...,

n+1

] to derive (by induction) the recursions

= a

, q

= 1, p

= a

+ 1, q

= a

;

= a

n−1

+ p

n−2

, q

= a

n−1

+ q

n−2

(n ≥ 2),

; a

,...,a

]:=

. (6.12)

If the sequence p

converges, then we express the limit as the inﬁnite

continued fraction expansion [a

; a

, a

,...].

Since from (6.12) we also get

n+1

− p

n+1

=−(p

n−1

− p

n−1

) for all n, (6.13)

one has, on dividing both sides by q

n+1

and iterating,

n+1

−

=−

n−1

n+1



−

n−1



n+1

−

(−1)

n+1

(6.14)

since p

− p

= 1/a

Note that the condition a

> 0(i ≥ 1) above ensures that q

> 0 for

all n ≥ 1 (as q

is deﬁned to be 1). Hence [a

; a

,...,a

] = p

well deﬁned for all n ≥ 0.

We will need to relax the above condition to

≥ 0 ∀i ≥ 0, a

> 0 for some m ≥ 1. (6.15)

If m ≥ 1 is the smallest integer such that a

> 0, then it is clear from

the expressions (6.5), (6.6) that [a

; a

,...,a

] ≡ a

+ [a

, a

,...,a

]

is well deﬁned with q

> 0 for n ≥ m. The recursions in (6.12) then hold

for n ≥ m + 2. Then (6.13) holds for all n ≥ m + 1. Hence, in place of

(6.14) one gets

n+1

−

= (−1)

n−m

m+1

n+1



m+1

−



(n ≥ m). (6.16)

4.6 Random Continued Fractions 327

Now the right-hand side is alternately positive and negative, and the

magnitude of the n-th term is nonincreasing in n,asq

n+1

≥ q

n−1

and

n+1

≥ q

n−1

. Therefore, one has

)

n+j

−

)

≤

m+1

n+1

)

m+1

−

)

∀n ≥ m, j ≥ 1. (6.17)

Therefore, [a

; a

,...,a

] ≡ p

converges to a ﬁnite limit if and only

if q

n+1

→∞as n →∞. We may use this to prove a result on general

stability of the Markov process X

(n ≥ 0) deﬁned by (6.1).

Proposition 6.1 If {Z

: n ≥ 1} is a nondegenerate nonnegative i.i.d.

sequence, then the Markov process X

(n ≥ 0) deﬁned by (6.1) on S =

(0, ∞) converges in distribution to a unique invariant probability, no

matter what the (initial) distribution of X

is.

Proof. Since Y

deﬁned by (6.4) has the same distribution as X

(for

every n), it is enough to show that Y

converges in distribution to the

same distribution, say, π , whatever X

may be. Since P(Z

> 0) > 0,

by the assumption of nondegeneracy, it follows from the (second) Borel–

Cantelli lemma that, with probability 1, Z

> 0 for inﬁnitely many

n. In particular, with probability 1, there exists m = m(ω) ﬁnite such

that Z

> 0. Then deﬁning p

= [Z

; Z

,...,Z

n+1

] in place of

; a

,...,a

] (i.e., take a

= Z

, a

= Z

j+1

, j ≥ 1), p

is well

deﬁned for n ≥ m = m(ω) (indeed, for n ≥ m(ω) − 1). Also, by recur-

sion (6.12) for q

, one has, for all n ≥ m + 2,

n+1

= a

n+1

+ q

n−1

= Z

n+2

+ q

n−1

n+1

= Z

n+2

+ q

n−1

=···=



j=m+1

j+2

+ q

m+1

≥

2[n/2]



i=2

[

m+2

]

i+2

≥ q

[

m+2

]

2[n/2]



i=2

[

m+2

]

i+2

, (6.18)

where [r/2] is the integer part of r/2. Note that, for the ﬁrst inequal-

ity in (6.18), we picked out terms Z

i+2

with i an even integer. For

the second inequality, we have used the fact that q

2 j

is increasing in j

(use the recursion q

2 j

= a

2 j

2 j−1

+ q

2 j−2

in (6.12)). Now there exists

328 Random Dynamical Systems: Special Structures

c > 0 such that P(Z

> c) > 0. Applying the (second) Borel-Cantelli

lemma, it follows that, with probability one, Z

> c for inﬁnitely many

n. This implies



j=1

2 j

→∞a.s. as N →∞. Hence q

n+1

→∞

a.s., proving that [Z

; Z

,...,Z

n+1

] converges a.s. to some ran-

dom variable X , say. Finally, note that Y

n+1

− [Z

; Z

,...,Z

n+1

] ≡

; Z

,...,Z

n+1

, X

] − [Z

; Z

,...,Z

n+1

] → 0 a.s., uniformly with

respect to X

as n →∞, by (6.17). Hence Y

converges in distribution

to X, irrespective of the initial X

, and so does X

We will next strengthen Proposition 6.1 by verifying that the splitting

hypothesis (H) of Theorem 5.1, Chapter 3, holds.

Theorem 6.1 Under the hypothesis of Proposition 6.1, the convergence

in distribution of X

to a unique nonatomic invariant probability is

exponentially fast in the Kolmogorov distance, uniformly for all initial

distributions.

Proof. Since the i.i.d. maps in (6.2) are monotone (decreasing) on

S = (0, ∞), in order to prove the theorem it is enough to verify that

the splitting hypothesis (H) of Theorem 5.1, Chapter 3, holds. For this

purpose note that there exist 0 < a < b < ∞ such that P(Z

≤ a) > 0

and P(Z

≥ b) > 0. Check that the formal expressions [a; b, a, b, a,...]

and [b; a, b, a, b,...] are both convergent. Indeed, for the ﬁrst q

≥

(ab + 1)

, q

2n+1

≥ b(ab + 1)

(n = 0, 1, 2,...), as may be checked by

induction on n, using (6.12). For the second expression, the correspond-

ing inequalities hold with a and b interchanged. Thus q

n+1

→∞in

both cases.

We will show that x

:= [a; b, a, b, a,...] < y

:= [b; a, b, a, b,...]

and that the splitting hypothesis (H) holds with z

= (x

+ y

)/2,

if N is appropriately large. For this we ﬁrst observe that y

−

> b − a. For, writing c = [a, b, a, b,...] in the notation of (6.6),

one has y

= b + c and x

= a + 1/(b + 1/c), so that y

− x

b − a + c

b/(bc + 1) > b − a. Now for any given n ≥ 1, the func-

tion f

, a

,...,a

):= [a

; a

,...,a

]isstrictly increasing in the

variable a

2 j

and strictly decreasing in the variable a

2 j+1

(2 j + 1 ≤

n), provided a

,...,a

are positive. To see this, one may use in-

duction on n as follows: For n = 1, 2, for example, check this by

looking at (6.11). Suppose the statement holds for some n ≥ 1.

Consider the function f

n+1

, a

,...,a

, a

n+1

). Then, by deﬁnition

4.6 Random Continued Fractions 329

of the continued fraction expression, f

n+1

, a

,...,a

, a

n+1

) =

, a

,...,a

+ 1/a

n+1

). If n is even, n = 2m, then by the in-

duction hypothesis f

, a

,...,a

+ 1/a

n+1

) > f

, a

,...,a

1/b

n+1

) ≡ f

n+1

, a

,...,a

, b

n+1

)ifa

n+1

< b

n+1

, proving f

n+1

strictly decreasing in the (n + 1)th coordinate. Similarly, if n is

odd, n = 2m + 1, then f

n+1

, a

,...,a

, a

n+1

) ≡ f

, a

,...,a

1/a

n+1

) < f

, a

,...,a

+ 1/b

n+1

)ifa

n+1

< b

n+1

, by the induction

hypothesis. Since in this representation of f

n+1

in terms of f

, the re-

maining coordinates a

,1≤ j < n are unaltered, by the induction hy-

pothesis, f

n+1

is strictly increasing in a

2 j

and strictly decreasing in a

2 j+1

(2 j + 1 < n, 2 j < n). The argument for the nth coordinate also follows

in the above manner. Thus the induction is complete.

Next, let N be such that the N th convergent p

of x

[a; b, a, b, a,...] differs from x

by less than ε := (z

− x

)/4 and

the N th convergent p



,say,ofy

= [b; a, b, a, b ...] differs from

by less than ε = (y

− z

)/4. Note that if one writes p

; a

,...,a

] then whatever be x, [a

; a

,...,a

, x] differs from x

by less than ε, since the difference between a number u and its (N + 1)th

convergent is no larger than that between u and its N th convergent.

(Take m = 0 in (6.16) and (6.17), and let j ↑∞in (6.17).) The same

is true of the (N + 1)th convergent of y

= [b; a, b, a, b,...]. Without

loss of generality, let N be even. By the argument in the preceding

paragraph, on the set A

={Z

≤ a, Z

≥ b, Z

≤ a,...,Z

N +1

≤ a},

one has

(x) ≡ [Z

; Z

,...,Z

N +1

, x] ≤ [a;

N terms

9 :; <

b, a, b,...,a, x]

≤ x

+ ε<z

∀x ∈ (0, ∞). (6.19)

Similarly, on the set A

={Z

≥ b, Z

≤ a, Z

≥ b,...,Z

N +1

≥ b},

(x) ≥ [b; a, b, a,...,b, x] ≥ y

− ε>z

∀x ∈ (0, ∞). (6.20)

Letting χ

= P( A

) ≥ δ

N +1

, χ

= P( A

) ≥ δ

N +1

, where δ

min{P(Z

≤ a), P(Z

≥ b)} > 0, and noting that {X

(x) < z

∀x ∈ (0, ∞)}, {X

(x) > z

∀x ∈ (0, ∞)} have the same probabilities as

(x) < z

∀x ∈ (0, ∞)} and {Y

(x) > z

∀x ∈ (0, ∞)}, respectively,

we have shown that (H) holds with χ = δ

N +1

. Since the i.i.d. maps in

(6.2) are strictly decreasing, it follows from Remark 5.4 of Chapter 3

that the unique invariant probability is nonatomic.

330 Random Dynamical Systems: Special Structures

Example 6.1 (Gamma innovation). Consider the case where the distri-

bution of Z

is (λ, β)(λ>0,β > 0), with density

λ,β

(z) =

(λ)

λ−1

−βz

(0,∞)

(z).

From (6.1) it follows that if X is a random variable having the invariant

distribution π on (0, ∞), then one has the distributional identity

= Z +

, (6.21)

where, on the right-hand side, X and Z are independent and Z has the

innovation distribution, which is (λ, β) in this example. By a direct

veriﬁcation, one can check that (6.21) holds if the distribution π of X

has the density

λ,β

(x) = c(λ, β)x

λ−1

−β(x +1/x)

(0,∞)

(x), (6.22)

where c(λ, β) is the normalizing constant,

c(λ, β) = 1



∞

λ−1

−β(x +1/x)

dx.

Note that the density of the random variable 1/ X = Y ,say,is

h(y) = c(λ, β)y

−λ−1

−β(y+1/y)

(0,∞)

(y).

It is a simple exercise to check that the convolution h ∗ g

λ,β

equals f

λ,β

(Exercise). This proves (6.21), establishing the invariance of π with den-

sity f

λ,β

4.6.3 Bernoulli Innovation

Consider the Markov process on the state space S = (0, ∞) deﬁned by

(6.1), where Z

(n ≥ 1) are i.i.d.,

P(Z

= 0) = α, P(Z

= θ ) = 1 − α, (6.23)

with 0 <α<1, θ>0, and X

is independent of {Z

: n ≥ 1}.IfX

converges in distribution to X, where X is some random variable having

the unique invariant distribution π on S = (0, ∞), then the probability

measure π is characterized by the distributional identity (6.21), where

, X has distribution π , and X and Z are independent. As before,

4.6 Random Continued Fractions 331

= denotes equality in law. As an immediate corollary of Theorem 6.1,

we have the following result:

Proposition 6.2

(a) The Markov process X

on S = (0, ∞) above has a unique invari-

ant probability π , and the Kolmogorov distance d

∗n

µ, π ) converges

to zero exponentially fast in n, uniformly with respect to the initial dis-

tribution µ.

(b) π is nonatomic.

The next proposition shows that the cases 0 <θ≤ 1 and θ>1 are

qualitatively different.

Proposition 6.3

(a) If 0 <θ ≤ 1, then the support of π is full, namely (0, ∞).

(b) If θ>1, then the support of π is a Cantor subset of (0, ∞).

For the proof of Proposition 6.3 we need two lemmas.

Lemma 6.1 Let 0 <θ ≤ 1. Then the set of all continued fractions

θ; a

θ,a

θ,...],a

’s are integers, a

≥ 0,a

≥ 1(i ≥ 1), comprises

all of (0, ∞).

Proof. Let x ∈ (0, ∞). Deﬁne a

= max{n ≥ 0: nθ ≤ x}.Ifx = a

θ,

then x = [a

θ]. If not, deﬁne r

x = a

θ +

. (6.24)

Since 0 <

<θ, r

≥ θ . Deﬁne a

= max{n ≥ 0: nθ ≤ r

}.If

= a

θ, x = [a

θ; a

θ]. If not, we deﬁne r

= a

θ +

, (6.25)

>θ, and let a

= max{n ≥ 0: nθ ≤ r

}. Proceeding in this way

we arrive at either a terminating expansion [a

θ; a

θ,...,a

θ]or

an inﬁnite expansion [a

θ; a

θ,a

θ,...]. We need to show that, in

the latter case, the expansion converges to x. Now use the rela-

tion (6.17) with m = 0, and α

θ in the place of a

(i ≥ 0). One gets

332 Random Dynamical Systems: Special Structures

= [a

θ; a

θ,...,a

θ], and x = [a

θ; a

θ,...,a

n−1

θ, a

θ +

n+1

], 1/r

n+1

<θ,

)

x −

)

n+1

. (6.26)

Since a

≥ 1 ∀i ≥ 1, it is simple to check as before, using (6.12), that

= 1, q

= a

θ ≥ θ, q

≥ q

= 1, q

≥ q

≥ θ ;

≥ q

, q

2n+1

≥ q

∀n;

= a

θq

n−1

+ q

n−2

≥ θ

+ q

n−2

∀n ≥ 2.

Hence q

≥ [

]θ

→∞, and (6.26) → 0asn →∞.

Remark 6.1 The arguments made in the above proof are analogous to

those for the case θ = 1. But the assertion in the lemma does not hold

for θ>1. The reason why the argument breaks down is that if θ>1,

then r

deﬁned by (6.25) may be smaller than θ.

Lemma 6.2 Let p

(n)

(x, dy) be the n-step transition probability, n =

1, 2,... of a Markov process on (S, S), where S is a separable metric

space and S its Borel sigma ﬁeld. Assume x → p

(1)

(x, dy) is weakly

continuous, and π is an invariant probability. If x

is in the support of

π and p

(n)

, dy) converges weakly to π , then the support of π is the

closure of ∪

∞

n=1

{support of p

(n)

, dy)}.

Proof. Let F denote the support of π , and G:=∪

∞

n=1

{support of

(n)

, dy)}.Fixε>0, n ≥ 1. Let B(y,δ) denote the open ball in S with

center y and radius δ>0. Suppose y

is such that p

(n)

, B(y

,ε)) >

> 0. Since lim inf

x→x

(n)

(x, B(y

,ε)) ≥ p

(n)

, B(y

,ε)), by weak

convergence, there exists δ

> 0 such that p

(n)

(x, B(y

,ε)) >δ

∀x ∈

B(x

,δ

). Then

π(B(y

,ε)) =

(n)

(x, B(y

,ε))π (dx)

≥ δ

π(B(x

,δ

)) > 0,

since x

is in the support F of π . This proves G ⊂ F.ToproveF ⊂

G ≡

closure of G, let y

∈ F.Ify

/∈

G, then there exists δ>0 such that

B(y

,δ) ∩ G =∅, which implies p

(n)

, B(y

,δ)) = 0 ∀n ≥ 1. This is

impossible since lim inf

n→∞

(n)

, B(y

,δ)) ≥ π(B(y

,δ)) > 0.