Беляк О.А., Дрезин С.В. Динамика материальной точки
Подождите немного. Документ загружается.


Ox
∆
∆ = ∆ + x,
∆
F = c∆ = c(∆ + x).
x
c∆ = mg sin α, ∆ =
mg
c
sin α.
x
m¨x = −c(∆ + x) + mg sin α
˙x(0) = v
0
x(0) = −∆
¨x + k
2
x = 0, k =
r
c
m
,
C
1
= −∆ = −
mg sin α
c
,
C
2
=
v
0
k
.
x =
v
0
k
sin kt −
mg
c
sin α cos kt.

Q m
c
1
c
2
A
B
x
c
1
c
2
O
F
1
Q
mg
F
2
l
1
+ l
2
AB Ox
mg, F , F Ox
−c
1
∆ − c
2
∆ + mg = 0.
∆ ∆
l
1
+ l
2
AB F F
∆ ∆
Q Ox
m¨x = −c
1
(∆ + x) −c
2
(∆ + x) + mg.
m¨x + (c
1
+ c
2
)x = 0, ¨x +
(c
1
+ c
2
)
m
x = 0,
k =
r
c
1
+ c
2
m
T =
2π
k
= 2π
r
m
c
1
+ c
2
c
1
c
2
c = c
1
+ c
2

v
0
x = C
1
cos kt + C
2
sin kt.
x(0) = 0, ˙x(0) = v
0
C
1
= 0, C
2
=
v
0
k
.
x = v
0
r
m
c
1
+ c
2
sin
r
c
1
+ c
2
m
t.
m
c
1
c
2
v
0
Ox AB
mg, F , F
x
a
1
a
2
BA
O
F
2
F
1
mgmg

AB
O
F a
1
= F a
2
.
∆ = ∆ = ∆ ,
F = c
1
∆ , F = c
2
∆ .
c
1
a
1
= c
2
a
2
.
Ox
m¨x = −c
1
(∆ + x) −c
2
(∆ + x) + mg.
Ox
−c
1
∆ − c
2
∆ + mg = 0, ∆ =
mg
c
1
+ c
2
,
¨x + k
2
x = 0, k =
r
c
1
+ c
2
m
.
v
0
x(0) = −∆ , ˙x(0) = v
0
.
x(t) = C
1
cos kt + C
2
sin kt = −
mg
c
1
+ c
2
cos kt +
v
0
k
sin kt.
T =
2π
k
= 2π
r
m
c
1
+ c
2
c = c
1
+ c
2

c
c
1
c
2
m
Ox
mg
F A F = F
c x
x
1
x
2
x = x
1
+ x
2
.
mg = c
1
x
1
, c
1
x
1
= c
2
x
2
, mg = cx.
O
A
FF
mg
x
F
2
F
1
mg
mg
c
=
mg
c
1
+
mg
c
2
,
1
c
=
1
c
1
+
1
c
2
,
c =
c
1
c
2
c
1
+ c
2
.

k =
r
c
m
=
r
c
1
c
2
(c
1
+ c
2
)m
,
T = 2π
s
(c
1
+ c
2
)m
c
1
c
2
.
x
0
v
0
Ox
x(0) = x
0
, ˙x(0) = −v
0
Ox m¨x = −cx.
x(t) = C
1
cos kt + C
2
sin kt.
x(t) = x
0
cos
r
c
1
c
2
(c
1
+ c
2
)m
t
− v
0
s
(c
1
+ c
2
)m
c
1
c
2
sin
r
c
1
c
2
(c
1
+ c
2
)m
t
.
E m
c
x
EE
α
l − l
0
l
0
l
O
O
O
O
1
O
1
O
1
FF
mg
x
N

O
1
l
0
F
0
= c(l − l
0
) l = OO
1
E O
E x
l
0
E
(l − l
0
) E
mg
F N E
Ox
m¨x = −F cos α,
F = c∆.
∆
l
∗
∆ = l
∗
− l
0
, l
∗
= O
1
E.
E
l
∗
=
l
sin α
∆ =
l
sin α
− l
0
.
m¨x = −c(l ctg α − l
0
cos α).
O
1
OE cos α ctg α
x
ctg α =
x
l
.

cos
2
α =
ctg
2
α
1 + ctg
2
α
,
cos α =
x/l
p
1 + (x/l)
2
, 0 < α 6 π/2.
cos α =
x
l
−
x
3
2l
3
+ O
x
l
5
.
m¨x +
c(l − l
0
)
l
x = 0,
k =
r
c(l − l
0
)
ml
, T = 2π
r
ml
c(l − l
0
)
F
0
= c(l − l
0
) E
T = 2π
r
ml
F
0
.
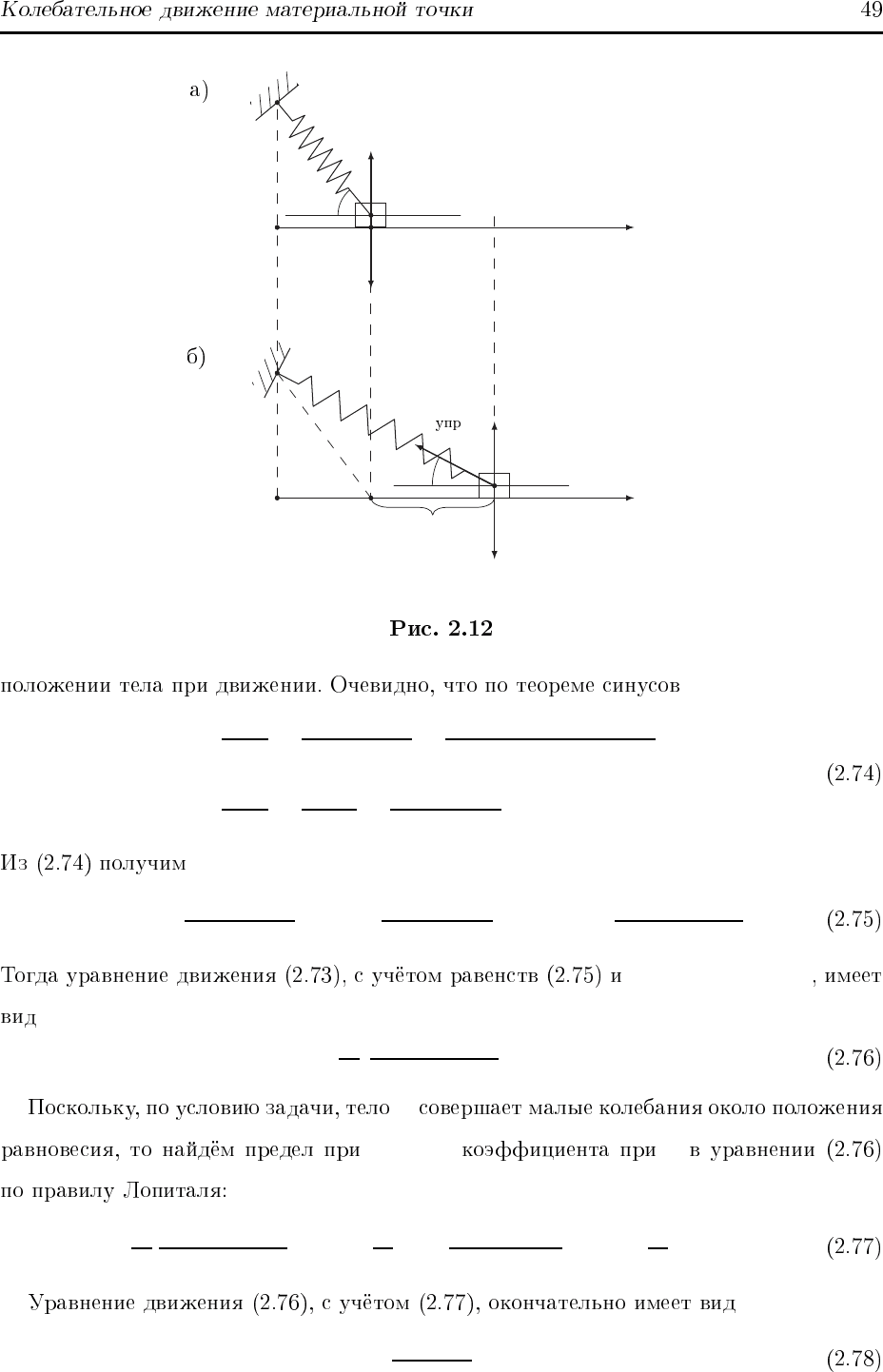
A m
c
B α = α
0
A
Ox
O
α = α
0
A
m¨x = −c∆ cos α,
∆ = l − l
0
OBA
1
l
0
l
O
N
x
B
B
N
A
A
1
mg
mg
x
O
1
α
0
α
O
O
1
F
xx
l
0
sin α
=
l
sin(π − α
0
)
=
x
sin(π − α − (π − α
0
))
,
l
0
sin α
=
l
sin α
0
=
x
sin(α
0
− α)
.
l = x
sin α
0
sin(α
0
− α)
, l
0
= x
sin α
sin(α
0
− α)
, l − l
0
= x
sin α
0
− sin α
sin(α
0
− α)
.
0 < α < α
0
< π/2
¨x + x
c
m
sin α
0
− sin α
sin(α
0
− α)
cos α = 0.
A
α → α
0
x
lim
α→α
0
c
m
sin α
0
− sin α
sin(α
0
− α)
cos α =
c
m
lim
α→α
0
cos α
cos(α
0
− α)
cos α =
c
m
cos
2
α
0
.
¨x +
c cos
2
α
0
m
x = 0.
k = cos α
0
r
c
m
,
T =
2π
cos α
0
r
m
c
.
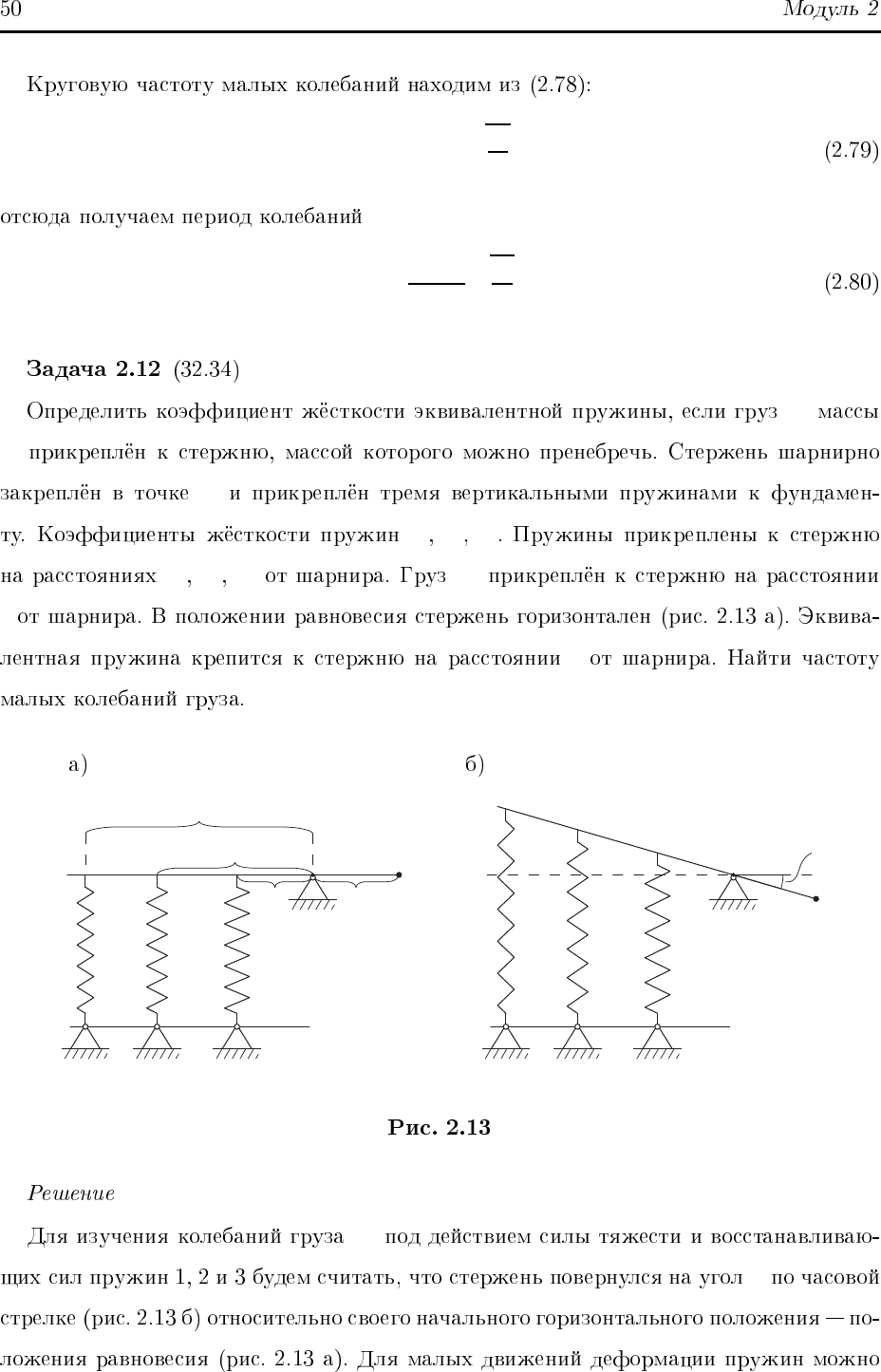
M
m
O
c
1
c
2
c
3
a
1
a
2
a
3
M
b
b
a
1
a
2
a
3
b
c
3
c
2
c
1
O
∆
1
∆
2
∆
3
M
c
3
c
2
c
1
M
O
ϕ
M
ϕ
