Белашов В.Ю., Чернова Н.М . Эффективные алгоритмы и программы вычислительной математики

Подождите немного. Документ загружается.

§ 1. Элементарная алгебра

Таблица 1.2

n Формула (1.8) (точное значение) Формула (1.9) Формула (1.10)

5 120 118.019172668 (1.65 %) 119.9999771 (1.9 e - 5 %)

10 3628800 3598695.75 (0.82 %) 3628800 (0 %)

15 1307674279936 1300430716928 (0.55 %) 1307674411008 (1.0 e - 5 %)

Процедура FCT может быть эффективно использована

при вычислении бинома Ньютона:

()ab Ca b

knkk

∑

(1.11)

и величины полинома

(...)

( , ,..., ) ...

...

aa a

Ckk k a a a

kk k

+++ =

=⋅

+++=

∑

⋅⋅⋅

, (1.12)

где суммирование проводится по всем наборам неотрица-

тельных целых чисел (k

,...,k

), для которых k

+ k

+... + k

= n. При этом C

, k

, ..., k

), вычисляемые по

формуле (1.5), называются полиномиальными коэффици-

ентами. Формула для определения количества полиноми-

альных коэффициентов имеет вид:

Ckk k r

kk k

(, ,..., )

...

+++=

∑

Рассмотрим процедуру-функцию вычисления бинома

Ньютона, в которой используется функция FCT в соответ-

ствии с формулой (1.11).

Формальные параметры процедуры. Входные: a, b

(тип real)- значения слагаемых a и b в выражении (1.11); n

(тип integer) - показатель степени бинома; k (тип integer) -

ключ, определяющий выбор алгоритма вычисления факто-

риала (см. описание параметров процедуры-функции

FCT). Выходной: функция binn (тип real) - значение би-

нома Ньютона.

UNCTION BINN (VAR A, B : REAL;

VAR N, K : INTEGER;): REAL;

VAR S,F1,F2,F3 : REAL; L,M : INTEGER;

BEGIN

BIN:=0;

F1:=FCT(N,K);

FOR L:=0 TO N DO

BEGIN

F2:=FCT(L,K);

M :=N-L;

F3:=FCT(M,K);

S :=F1/(F2*F3);

BIN:=BIN+S*EXP(A*LN(M)+B*LN(L));

END;

END; {*** BINN ***} .

Оценка точности вычислений бинома проводилась при

тестировании программы для n = 5, 10, 15, 20, 30; k = - 1

(данное значение k соответствует точному вычислению

факториала в процедуре-функции FCT) и различных пара-

метров a и b. Результаты, полученные при n = 5, 7, 10, 15;

a = =1.5; b = 2.5, -2.5, и соответствующие им величины от-

носительной погрешности представлены в табл. 1.3.

Таблица 1.3

Параметр Значение бинома при использовании формулы

n a b (1.8) (1.10)

1.5

2.5

-2.5

2.5

-2.5

2.5

-2.5

2.5

-2.5

1024 (+ 0%)

— 1 (+ 0%)

16384 (+ 0%)

— 1 (+ 0%)

1048576 (+ 0%)

1.00098 (+9.766e-2%)

21073741696 (+1.2e-5%)

—

1024.1940 (+1.89e-2%)

— 0.8770 (+11.3%)

16385.5449 (+9.4e-3%)

0.125 (+112.6%)

1048610 (+3.2e-3%)

—

1073747328 (+5.1e-4%)

—

Из таблицы видно, что при b > 0 с увеличением n точ-

ность вычислений растет и практически ограничена толь-

ко ошибками округления,

для отрицательных же b уже

при n>10 в случае использования формулы (1.8) и при n ~

5 в случае использования формулы (1.10) для факториала

погрешность резко возрастает, что связано с вычитанием

больших чисел в правой части равенства (1.11). Поэтому

при b < 0 рекомендуется использовать элементарную фор-

мулу (a + b)

, на современных быстродействующих ЭВМ

это даст некоторый выигрыш во времени счета.

Заметим, что совершенно аналогично может быть по-

строена процедура вычисления величины полинома (1.12),

поэтому она здесь не приводится.

Когда известно некоторое сочетание из n по m, тогда

вычисление следующего по порядку сочетания мо-

жет быть эффективно осуществлено с помощью процеду-

ры генератора сочетаний [Агеев и др., 1976], которая обра-

зует следующее по порядку сочетание из n целых чисел по

m, если заданы n, m и предшествующее сочетание.

Формальные параметры процедуры. Входные: n, m

(тип integer); вектор j [1:m] (тип integer) - предшествую-

щее сочетание. Выходной: тот же вектор j, в котором це-

лые числа меняются от 0 до n - 1 и всегда при входе и вы-

ходе из процедуры составляют монотонную строго возрас-

тающую последовательность. Если входной вектор j сос-

тоит из нулей, то в качестве первого сочетания будет по-

лучено (n - m, ..., n - 1). Такое же сочетание получится и

Глава 1. Численные методы алгебры

после сочетания (0, 1,..., k - 1), являющегося последним

значением вектора j в этом цикле

PROCEDURE COMB (N, M : INTEGER; VAR J : MAS1);

VAR A, B, L : INTEGER;

BEGIN

FOR B:= 1 TO M DO

IF J[B]>B THEN

BEGIN

A:=J[B]-B-1;

FOR L:=1 TO B DO J[L]:=L+A;

EXIT;

END;

B:=N-M-1;

FOR L:=1 TO K DO

J[L]:=B+L;

END; {*** COMB ***}.

Данный алгоритм был переведен авторами с языка AL-

GOL на язык PASCAL и проверен на машине IBM PC/AT-

286 для тех же значений входных параметров, что и в

работе Агеева и др. (1976), n = 4, k = 3. В качестве на-

чального вектора j был выбран вектор (0,0,0). В результате

последовательных обращений к процедуре получены сле-

дующие сочетания: (1,2,3), (0,2,3), (0,1,3), (0,1,2), что пол-

ностью соответствует результатам тестирования ALGOL-

программы, приведенными в работе Агеева и др. (1976).

1.3. ВЫЧИСЛЕНИЕ СИМВОЛА ЯКОБИ

⎛

⎝

⎜

⎞

⎠

⎟

Символ Якоби

⎛

⎝

⎜

⎞

⎠

⎟

- функция, определяемая для всех

целых a, взаимнопростых, с заданным нечетным целым

числом P > 1. Так, если P = p

...p

- разложение числа

P на простые сомножители не обязательно различные, то

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

××

⎛

⎝

⎜

⎞

⎠

⎟

...

где

⎛

⎝

⎜

⎞

⎠

⎟

- символы Лежандра [Виноградов, 1953], т.е.

арифметические функции чисел a и р

определенные для

простых нечетных р

и целых а, не делящихся на P, при-

чем

⎛

⎝

⎜

⎞

⎠

⎟

= 1, если сравнение x

≡ a(mod p

) разрешимо, а

в противном случае

⎛

⎝

⎜

⎞

⎠

⎟

= -1. Часто символ Лежандра, а

следовательно, и символ Якоби, который является его

обобщением, доопределяют для чисел a, делящихся на p

(для символа Якоби соответственно на P), полагая, что в

этом случае

⎛

⎝

⎜

⎞

⎠

⎟

= 0. Символ Якоби обладает свойства-

ми, аналогичными свойствам символа Лежандра, а имен-

но:

1) если a ≡ b (mod P), то

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

;

⎛

⎝

⎜

⎞

⎠

⎟

= 1;

()

(

⎛

⎝

⎜

⎞

⎠

⎟

≡

−12/

mod

)

;

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

⎛

⎝

⎜

⎞

⎠

⎟

;

()

⎛

⎝

⎜

⎞

⎠

⎟

⋅

⎛

⎝

⎜

⎞

⎠

⎟

=−

−⋅−

12 12()/()/

где P, Q - положительные нечетные взаимно простые чис-

ла (квадратичный закон взаимности, который впервые

доказан для символа Лежандра Гауссом в 1876 г.);

()

−

⎛

⎝

⎜

⎞

⎠

⎟

=−

−

()

;

()

⎛

⎝

⎜

⎞

⎠

⎟

=−

×−/

Перечисленные свойства позволяют легко вычислять

символ Якоби, не прибегая к решению сравнений. Заме-

тим, что при фиксированном P символ Якоби является

действительным характером мультипликативной группы

классов вычетов по модулю P.

Процедура SYJAC, построенная по алгоритму, учиты-

вающему приведенные свойства, вычисляет значение сим-

вола Якоби

⎛

⎝

⎜

⎞

⎠

⎟

по квадратичному закону взаимности. При

этом полагается следующее (табл. 1.4):

Таблица 1.4

Условие

Значение символа

Якоби ...

P - четное Не определено

P - нечетное 2

P - простое и a является квадратич-

ным невычетом числа m

- 1

Если a и P имеют нетривиальный

общий множитель

Остальные случаи 1

Формальные параметры процедуры. Входные: a, p

(тип integer). Выходной: r (тип integer) - значение символа

Якоби.

PROCEDURE SYJAC (A, P : INTEGER; VAR R : INTEGER);

VAR K : INTEGER; Z, Q : BOOLEAN;

LABEL : START, CYCLE;

UNCTION PARITY (X:INTEGER): BOOLEAN;

{

*** ???????? ??????? PARITY TRUE, ???? ? -

??????, ? FALSE - ? ????????? ?????? *** }

BEGIN

IF (X DIV 2 * 2) = X THEN

PARITY := TRUE

ELSE

PARITY := FALSE;

ЕND; {***PARITY***}

§ 1. Элементарная алгебра

BEGIN

START:

IF NOT PARITY (P) THEN

BEGIN

R := 2:

EXIT;

END;

Z := TRUE;

CYCLE:

REPEAT

A:=A - A DIV P * P;

Q := FALSE;

IF A > 1 THEN

BEGIN

WHILE NOT PARITY (A) DO

BEGIN

Q:= NOT Q;

A:=A DIV 2;

END;

IF Q AND PARITY ((SQR(P)-1) DIV 8) THEN

Z := NOT Z;

IF A ≠ 1 THEN

BEGIN

IF PARITY((P-1)*(A-1) DIV 4) THEN

Z:= NOT Z;

K:=P;

P:=A;

A:=K;

END;

UNTIL A <= 1;

IF A=0 THEN

R:= 0

ELSE

IF Z THEN

R := 1

ELSE

R:= -1;

END.

Приведенный алгоритм был переведен авторами с язы-

ка ALGOL на язык PASCAL и проверен на машине IBM

PC/AT-286 для тех же значений входных параметров, что

и в работе Агеева (1976). В результате тестирования было

получено:

⎛

⎝

⎜

⎞

⎠

⎟

= 1 (a = 5 - квадратичный вычет);

⎛

⎝

⎜

⎞

⎠

⎟

= -1 (a = 3 - квадратичный невычет);

⎛

⎝

⎜

⎞

⎠

⎟

= 2 (p = 12 - четное), что полностью соответст-

вует результатам тестирования программы на языке

ALGOL, приведенным в работе Агеева и др. (1976).

1.4. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА

НА МНОЖИТЕЛИ

Многочлен (целая рациональная функция) относитель-

но x

,..., x

есть сумма конечного числа членов вида

, где каждое k

ax x x

⋅×× ...

- целое неотрицатель-

ное число. Наибольшее значение суммы k

+ k

+ ...+ k

встречающееся в каком-либо из членов, называется сте-

пенью многочлена. В простейшем случае, когда x

= x

=...= x

= x и наибольшее значение суммы степеней

, многочлен принимает вид

∑

Paxaxax ax

nni

≡⋅=++++

−

∑

...

. (1.13)

Выражение (1.13) называется канонической формой

представления целой рациональной функции. Если

многочлен (1.13) при n > 1 может быть представлен в виде

произведения многочленов низших степеней, он называет-

ся приводимым. Возможность разложения на множители

многочленов степени n > 1 зависит от области определе-

ния коэффициентов. В частном случае, когда область

определения коэффициентов есть множество действи-

тельных чисел, любая целая рациональная функция n-й

степени может быть разложена на множители первой и вто-

рой степени (основная теорема алгебры [Бронштейн, Се-

мендяев, 1981] ). Приведенная нами процедура FACTORS

позволяет найти все рациональные линейные множители

x+v

), 1 < i < r многочлена (1.13) в частном случае,

когда область определения коэффициентов сужена до

множества целых чисел. При этом находится также

наибольший общий делитель c коэффициентов a

. Суть

метода состоит в том, что находятся все делители p коэф-

фициента a

и все делители q коэффициента a

, (причем 1

< p < |a

| и 1< q < <|a

|). Далее составляются все

возможные пары из найденных p и q и проверяется, не яв-

ляется ли двучлен (px - q) множителем многочлена.

Формальные параметры процедуры. Входные: n

(тип integer)- степень многочлена; a[0:n] (тип integer) -

массив коэффициентов многочлена. Выходные: u[1:r],

v[1:r] (тип integer) - массивы коэффициентов соответ-

ственно при первых и нулевых степенях x в рациональных

линейных множителях; r (тип integer) - количество линей-

ных множителей в разложении многочлена; c (тип integer)

- наибольший общий делитель коэффициентов a

много-

члена.

ROCEDURE FACTORS (N : INTEGER; A : MAS1;

VAR U,V : MAS1; VAR R,C : INTEGER);

LABEL ZERO;

VAR I, F, G, P, Q : INTEGER;

BEGIN

R:=0;

C:=1;

Глава 1. Численные методы алгебры

ZERO:

IF A[N]=0 THEN

BEGIN

N:=N-1;

R:=R+1;

U[R]:=1;

V[R]:=0;

GOTO ZERO;

END; { *** ZERO***}

FOR P:=1 TO ABS(A[0]) DO

IF (A[0] DIV P * P) = A[0] THEN

BEGIN

{

*** ??????? ???????? P, ???????????

?????????

???????????? A

***}

FOR Q:=1 TO ABS(A[N]) DO

BEGIN

{

*** ?????? Q ≠ 0, ?????????? ?????????? A

***}

IF Q<>1 THEN

REPEAT

IF (A[N] DIV Q * Q)=A[N] THEN

BEGIN

FOR I:=0 TO N DO

IF (A[I] DIV Q * Q) = A[I] THEN

FOR I:=0 TO N DO

A[I]:=A[I] DIV Q;

C := C * Q;

END

UNTIL (A[N] DIV Q * Q)<>A[N];

REPEAT

F:=A[0];

G:=1;

FOR I:=1 TO N DO

BEGIN

G:=G*P;

F:=F*Q+G*A[I]

END;

IF F=0 THEN INC(R);

U[R]:=P;

V[R]:=Q;

FOR I:=0 TO N DO

BEGIN

A[I]:=F:=(A[I]+F) DIV P;

F:=F*Q;

END;

N:=N-1;

IF N=0 THEN

BEGIN

C:=C*A[0];

EXIT

END

ELSE

Q:=-Q;

UNTIL (N<>0) OR (Q<0);

END;

IF N=0 THEN C:=C*A[0];

END.

Данный алгоритм был переведен авторами с языка AL-

GOL стереотипного переиздания [Агеев и др., 1976] сокра-

щенной и ординарно переработанной процедуры, опубли-

кованной в работе [Relph, 1962], на язык PASCAL и прове-

рен на машине IBM PC/AT-286 для многочленов, что из

работы Агеева и др. (1976). При этом были получены сле-

дующие разложения, полностью совпадающие с результа-

тами Агеева и др. (1976):

≡

- 29 x

+ 78x - 40 = 1*(x - 4) (x - 5) (3x - 2);

≡ x

- 6x

+ 32 = 1*(x + 2) (x - 4) (x - 4).

1.5. ВЫЧИСЛЕНИЕ КОРНЕЙ ПОЛИНОМОВ

С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ

В ФОРМЕ ПРОСТЫХ ДРОБЕЙ

Число x

называется корнем (нулем) целой рациональной

функции f(x) с действительными коэффициентами, если

fx a x

jnk

()=⋅

−

∑

. (1.14)

Вычисление корней полиномов, таким образом, сво-

дится к решению алгебраических уравнений (1.14). Для

нахождения рациональных корней полиномов с целыми

коэффициентами обычно используется хорошо известная

схема Горнера [Корн, Корн, 1978; Бронштейн, Семендяев,

1981]. В алгоритме применено предложенное в работе

[Pek, 1961] расширение этой схемы, суть которого состоит

в следующем. Полином (1.13) с целыми коэффициентами

при a

⋅ a

≠

0 имеет в качестве корня несократимую дробь

p/q тогда и только тогда, когда

apq

knk

−

∑

⋅⋅ =

Кроме того, q должно быть множителем a

, а p - мно-

жителем a

. Ненулевые рациональные корни p/q могут

быть выведены на внешний носитель информации в файл,

имя которого передается при вызове процедуры.

Формальные параметры процедуры. Входные: a

(тип integer) - одномерный массив размером от 0 до n, в

котором размещают коэффициенты полинома (1.13); n

(тип integer) - степень полинома; k (тип string) - имя фай-

ла на внешнем носителе (магнитном диске), в который

будут записываться результаты счета. Выходные: p, q (тип

integer) - числители и знаменатели найденных рациональ-

ных корней, выводятся на внешний носитель.

PROCEDURE RATF (A : MAS1; VAR N : INTEGER;

K: STRING);

VAR I, P, Q, R, T, F, G, A0, AN : INTEGER; F : TEXT;

BEGIN

A0:=ABS(A[0]);

AN:=ABS(A[N]);

SSIGN (F,K);

REWRITE (F);

FOR P:=1 TO A0 DO

BEGIN

§ 2. Решение нелинейных алгебраических уравнений с одной переменной

{

*** ???? P ? Q ?? ???????? ??????????? ?????????????

?????????????? A[0] ? A[N], ????????? ?? ????? ????? ???

??????????? ? ??????????????? ?????? ????? ***}

IF (A0 DIV P * P) = A0 THEN

BEGIN

FOR Q:=1 TO AN DO

BEGIN

IF (AN DIV Q * Q) = AN THEN

BEGIN

{*?????????? ???????? ??? ????????, ???????? ?? P/Q

??????, ??? ???? ??????????? ???????? R ???? ????????

?????? ?????????? ?????????? ? ???????? ***}

F := A[0];

G := A[0];

T := P;

FOR I:=1 TO N DO

BEGIN

R := A[I]*T;

F:=F*Q+R;

G:=-G*Q+R;

T:=T*P

END;

IF F=0 THEN

WRITE (F,P:10:5,' ',K:5,Q:10:5);

IF G=0 THEN

WRITE (F,P:10:5,' ',K:5,Q:10:5);

END;

END; {**Q**}

END;

END; {**P**}

END.

Процедура, в которой представлен исправленный,

ординарно переработанный и модифицированный алго-

ритм [Perry, 1962], переведена авторами с языка ALGOL

[Агеев и др., 1976] на язык PASCAL с сохранением ориги-

нального синтаксиса процедуры и проверена на машине

IBM PC/AT-286 для тех же полиномов, что и в указанной

выше работе :

(

)

Pxxx

36 3 14 3≡− + + + ;

При этом были получены результаты, полностью сов-

падающие с результатами Агеева и др. [1976]:

()

Pxxx

24 22 3≡− − − +

для

(

)

: x

= -

, x

= -

;

для

(

)

: x

, x

= -

, x

Из результатов тестирования процедуры видно, что во

втором случае x

= x

, и, кроме того, выдается избыточ-

ное значение корня p/q, в котором p и q содержат общий

множитель (это было также отмечено в работе [Halstead,

1962] для алгоритма Перри [Perry, 1962] ).

§ 2. pexemhe mekhmeim{u

`kceap`h)eqjhu rp`bmemhi q ndmni oepelemmni

Нелинейное алгебраическое уравнение с одной пе-

ременной в общем случае может быть записано в виде

F(x) = 0, (1.15)

где функция F(x) определена и непрерывна на конечном

или бесконечном интервале a < x < b.

Всякое значение ξ ∈ [a, b], обращающее функцию F(x)

в нуль, т.е. когда F(ξ) = 0, называется корнем уравнения

(1.15) или нулем функции F(x). Число ξ называется корнем

k-й кратности, если при x =

ξ вместе с функцией F(x)

равны нулю и ее производные до порядка (k - 1) вклю-

чительно:

F(x) = F'(x) = ... = F

(л - 1)

(x) = 0.

Однократный корень называется простым. Два урав-

нения называются равносильными (эквивалентными), если

множества их решений совпадают. Нелинейные уравнения

с одной переменной подразделяются на алгебраические,

когда функция F(x) в формуле (1.15) является

алгебраической, и трансцендентные в противном случае.

Большинство алгебраических и трансцендентных нелиней-

ных уравнений вида (1.15) аналитически (т.е. точно) не

решается, поэтому на практике для нахождения корней

часто используются численные методы. Рассмотрим неко-

торые из них [Березин, Жидков, 1962; Бахвалов, 1973а,

1973б и др.].

Задача численного нахождения действительных и ком-

плексных корней уравнения [1.15] обычно состоит из двух

этапов: отделения корней, т.е. нахождения достаточно

малых окрестностей рассматриваемой области, в которых

содержится одно значение корня, и уточнения корней, т.е.

их вычисления с заданной степенью точности в некоторой

окрестности. В связи с этим рассмотрим вначале задачу

отделения корней, а затем ряд итерационных методов их

уточнения.

2.1. ЗАДАЧА ОТДЕЛЕНИЯ КОРНЕЙ.

УТОЧНЕНИЕ КОРНЕЙ МЕТОДОМ

ПОЛОВИННОГО ДЕЛЕНИЯ

(МЕТОД ДИХОТОМИИ)

В общем случае редко удается точно найти все корни в

алгебраических уравнениях, а если к тому же коэффи-

циенты в уравнении даны с погрешностью, то вопрос о

точном определении корней вообще теряет всякий смысл.

Однако если предположить, что задано уравнение типа

(1.15), то тогда без ограничения общности можно утверж-

дать, что F(х) имеет корни, для которых существует ок-

рестность

(

)

±δ

, содержащая только один простой корень.

Такой корень иногда называют изолированным. В резуль-

тате общая задача нахождения корней или нулей функции

будет состоять из следующих этапов:

Глава 1. Численные методы алгебры

1) отделения корней, т.е. установления интервала

, где содержится один и только один корень урав-

нения;

[,]−+δδ

2) задачи уточнения одним из известных методов най-

денного корня ξ с заданной погрешностью ε.

Предположим теперь, что найден отрезок [а, b] такой,

что F(а)F(b) < 0. Тогда, согласно теореме Больцано-Коши

[Бахвалов, 1973б], внутри отрезка [а, b] существует точка

ξ, в которой F(ξ) = 0. Далее необходимо убедиться, что

найденная точка ξ единственная на отрезке [а, b]. Одним

из методов является деление отрезка на несколько частей,

например на четыре, и проверка на концах каждого из от-

резков знака функции.

Нули функции на практике вычисляют приближенно

несколькими способами. Одним из самых распростра-

ненных и не очень точных является графический метод,

заключающийся в том, что F(х) представляют как F(х) =

=ϕ(х) + ψ(х), где ϕ(х) и ψ(х) более простые по сравнению

с F(х) функции. Далее строят два графика y = ϕ(х); y =

ψ(х) и определяют точки их пересечения. Этим методом

выгодно решать уравнения вида х

+ ах + b = 0 или ах + b +

sin(сх)= = 0 и т.п. Но следует помнить, что этот метод дает

лишь грубое приближение решения.

Другим, не менее распространенным является метод про-

изводных. Он заключается в том, что ищут и приравнивают к

нулю производную функции F'(х). Затем на отрезках

рассматривают знак функции

F'(х), где х

()()(

−∞ +∞,, , ,... ,xxx x

n112

)

- корни уравнения F'(х) = 0. Таким образом,

всю числовую ось разбивают на два интервала и более.

Этот метод еще называют методом экстремумов функции.

Если исследуемая функция представлена полиномом n-

й степени, то используют метод удаления корней: опреде-

ляют один корень, и по теореме Виетта функцию F(х)

представляют как F(х) = g(х)(х - х

), где x

- первый най-

денный корень, а g(х) - полином степени (n - 1). Для про-

верки

кратности корня x

следует подставить в g(х), и если

g(x

) = 0, то говорят, что x

является кратным корнем, а

F(х) записывается F(х) = g(х)(х - x

)

, где g(х) - теперь по-

лином степени (n - 2). Следуя этому процессу, можно уда-

лить все корни, т.е. представить

fx x x

() ( )=−

∏

Чтобы погрешность с каждым шагом не увеличива-

лась, а очередной корень определялся с высокой степенью

точности, следует уточнение корня делать по F(х), а не по

g(х). Это особенно важно, когда удалено много (больше

половины) корней.

Hа практике предполагаемые корни уточняют различ-

ными специальными вычислительными методами. Одним

из них можно назвать метод дихотомии (бисекции, поло-

винного деления), относящийся к итерационным. Он состо-

ит в построении последовательности вложенных отрезков,

на концах которых F(х) имеет разные знаки. Каждый по-

следующий отрезок получают делением пополам предыду-

щего. Этот процесс построения последовательности вложен-

ных отрезков позволяет найти нуль функции (F(х) = 0) с лю-

бой заданной точностью.

Опишем подробно один шаг итерации. Пусть на k-м

шаге найден отрезок [а

, b

], на концах которого F(х) меняет

знак. Заметим, что обязательно [а

, b

] ∈ [а, b]. Разделим те-

перь отрезок [а

, b

] пополам и выделим F(ξ), где ξ - сере-

дина [а

, b

]. Здесь возможны два случая: первый, когда

F(ξ) = 0, тогда мы говорим, что корень найден; второй,

когда F(ξ) ≠ 0, тогда сравниваем знак F(ξ) с F(а

) и F(b

) и

из двух половин [а

, ξ] и [ξ, b

] выбираем ту, на концах ко-

торой функция меняет свой знак. Таким образом, а

= а , b

= ξ, если F(ξ)F(а

) < 0 , и а

= ξ , b

= b, если F(ξ)F(b

) < 0.

При заданной точности ε деление пополам продолжают

до тех пор, пока длина отрезка не станет меньше 2ε

, тогда

координата середины последнего найденного отрезка и есть

значение корня требуемой точности.

Метод дихотомии — простой и надежный метод поис-

ка простого корня

уравнения F(х) = 0. Он сходится для

любых непрерывных функций F(х), в том числе и недиф-

ференцируемых. Недостатки метода:

1) проблема определения отрезка, на котором функция

меняет свой знак (как правило, это отдельная вычисли-

тельная задача, наиболее сложная и трудоемкая часть ре-

шения);

2) если корней на выделенном отрезке несколько, то

нельзя заранее сказать, к какому из них сойдется процесс;

3) не применим к корням четной кратности;

4) для корней нечетной, но высокой кратности метод

неустойчив, дает большие ошибки;

5) медленно сходится. Для достижения ε необходимо

выполнить N итераций

, т.е. для получения 3 верных цифр

(

ε = 0.0005) надо выполнить около 10 итераций, если

отрезок имеет единичную длину.

Программа, по которой можно вычислить корни ме-

тодом дихотомии, построена по следующему алгоритму:

Øàã 1. Определить входные параметры А, В, ЕРS.

Øàã 2. Присвоить: А1 ⇐ А; В1 ⇐ В; К ⇐ 0.

Øàã 3. Присвоить: Х1 ⇐ А1; Х2 ⇐ В1; К ⇐ К + 1; Х3

⇐ (В1+А1)/2.

Øàã 4. Если F(Х1) × F(Х3) < 0, то перейти на шаг 5

иначе на шаг 7.

Øàã 5. Присвоить: В1 ⇐ Х3.

Øàã 6. Если | А1 - В1| < ЕРS, то перейти на шаг 10 ина-

че на шаг 3.

Корень х называется простым, если F(x) = 0, а F'(x) ≠ 0.

N = lоg

(b - а) / ε.

§ 2. Решение нелинейных алгебраических уравнений с одной переменной

Øàã 7. Если F(Х2) × F(Х3) < 0, то перейти на шаг 8

иначе на шаг 11.

Øàã 8. Присвоить: А1 ⇐ Х3.

Øàã 9. Перейти на шаг 6.

Øàã 10. Печать: Х3 - корень уравнения; К - количес-

тво итераций.

Øàã 11. | А1 - В1| / 2 - погрешность решения.

Øàã 12. Конец программы.

Это наиболее простое решение задачи, но не самое эф-

фективное. Эффективность можно повысить, если:

1) заменить произведения F(х

)⋅F(х

) и F(х

)⋅F(х

) на

использование встроенной функции sign(х, у). В тех версиях

языка, где нет этой встроенной функции, можно заранее на-

писать соответствующую процедуру;

2) определить процедуру-функцию, вычисляющую F(х)

только один раз;

3) заменить в операторе цикла медленный оператор

(А+В)/2 на более быстрый (А+В)*0.5. Заметим, что именно

для этой программы данное усовершенствование будет не-

заметно, хотя в случае больших программ учет скорости

выполнения операций в машине дает ощутимый резуль-

тат.

Формальные параметры процедуры. Входные: a, b

(тип real) - определяют длину отрезка; eps (тип real) - оп-

ределяет заданную точность вычислений; it (тип integer) -

определяет наибольшее разрешенное количество итераций

(для избежания зацикливания процесса в случае непра-

вильного определения отрезка). Выходные: х (тип real) - в

нем содержится искомый корень сравнения; k (тип integer) -

в него заносится количество выполненных итераций.

Учитывая все замечания, окончательный вариант про-

цедуры BISECT может быть следующим:

PROCEDURE BISECT (A,B,EPS :REAL; IT:INTEGER;

VAR X : REAL; VAR K:INTEGER);

VAR A1, B1: REAL; X1, X2, X3 : INTEGER;

BEGIN

K := 0;

X1 := SIGN (FUNC(A));

X2 := SIGN (FUNC(B));

A1 := A;

B1 := B;

REPEAT

INC (K);

X := (A1+B1)*0.5;

X3 := SIGN (FUNC (X));

IF X3=0 THEN EXIT;

IF ABS(B1-A1)<(2*EPS) THEN EXIT;

IF (X1=X2) AND (X2=X3) THEN EXIT;

IF X1=X3 THEN

BEGIN

A1 := X;

X1 := X3;

END

ELSE

BEGIN B1 := X;

X2 := X3;

END;

UNTIL K>IT;

END.

Перед началом работы программы определяют

FUNC(x) - процедуру-функцию, по которой вычисляют

значения F(х). Тип функции должен быть вещественным.

Если в библиотеке стандартного математического обеспе-

чения отсутствует процедура-функция SIGN, то ее следует

написать самостоятельно.

Предложенная процедура проверялась на примере реше-

ния уравнения x

- 5 sin x = 0.

Графическим методом находился отрезок, на котором

располагался один из корней данного уравнения [1.57;

3.14]; (второй корень тривиальный, х = 0 находится легко).

Для того, чтобы найти корень на отрезке [1.57; 3.14] с ука-

занной точностью, полагали ерs = 0.0005.

Результаты проверки работы предлагаемой процедуры

приводятся в табл. 1.5.

Таблица 1.5

Отрезок Номер

Левый конец Правый конец Центральная точка итерации

А sign (А) В sign (В) x sign (x) k

1.0 — 1 4.0 +1 2.5000 0

1.000000 — 1 2.500000 +1 1.750000 +1 1

1.750000 — 1 2.500000 +1 2.125000 +1 2

1.750000 — 1 2.125000 +1 1.937500 — 1 3

1.937500 — 1 2.125000 +1

2.031250

— 1 4

2.031250 — 1 2.125000 +1 2.078125 — 1 5

2.078125 — 1 2.125000 +1 2.101563 — 1 6

2.101563 — 1 2.125000 +1 2.089844 +1 7

2.101563 — 1 2.089844 +1 2.083984 +1 8

2.101563 — 1 2.083984 +1 2.086914 — 1 9

Глава 1. Численные методы алгебры

2.086914 — 1 2.083984 +1 2.085449 +1 10

Окончаниие таблицы 1.5

Отрезок Номер

Левый конец Правый конец Центральная точка итерации

А sign (А) В sign (В) x sign (x) k

2.086914 — 1 2.085449 +1 2.086182 — 1 11

2.086182 — 1 2.085449 +1 2.085815 +1 12

2.085815 — 1 2.086182 +1 2.085999 — 1 13

2.085815 — 1 2.085999 +1 2.085907 +1 14

2.085815 — 1 2.085907 +1 2.085953 — 1 15

2.085907 — 1 2.085953 +1 2.085930 +1 16

2.085930 — 1 2.085953 +1 2.085941 — 1 17

РЕШЕНИЕ: Х = 2.085936; F(x) = 0.0000066938; К = 18

2.2. ПРИБЛИЖЕННОЕ РЕШЕНИЕ

УРАВНЕНИЯ F(x) = 0

МЕТОДОМ ХОРД (СЕКУЩИХ)

После того, как отрезок [а, b], на котором F(х) меняет

свой знак, определен (см. п. 2.1), можно уточнять корень

разными методами. Метод дихотомии требует большого

количества итераций и не всегда сходится к искомому кор-

ню [Бахвалов, 1973а]

Если отрезок [а, b] делят не пополам, а в отношении

F(а):F(b), то получают точку x, расположенную ближе к

предполагаемому корню уравнения по сравнению с точкой,

найденной методом дихотомии. Новое приближенное зна-

чение корня принимается:

()

, где

()

abfx

fb fx

−⋅

−

. (1.16)

При n ≠ 0 полагаем х

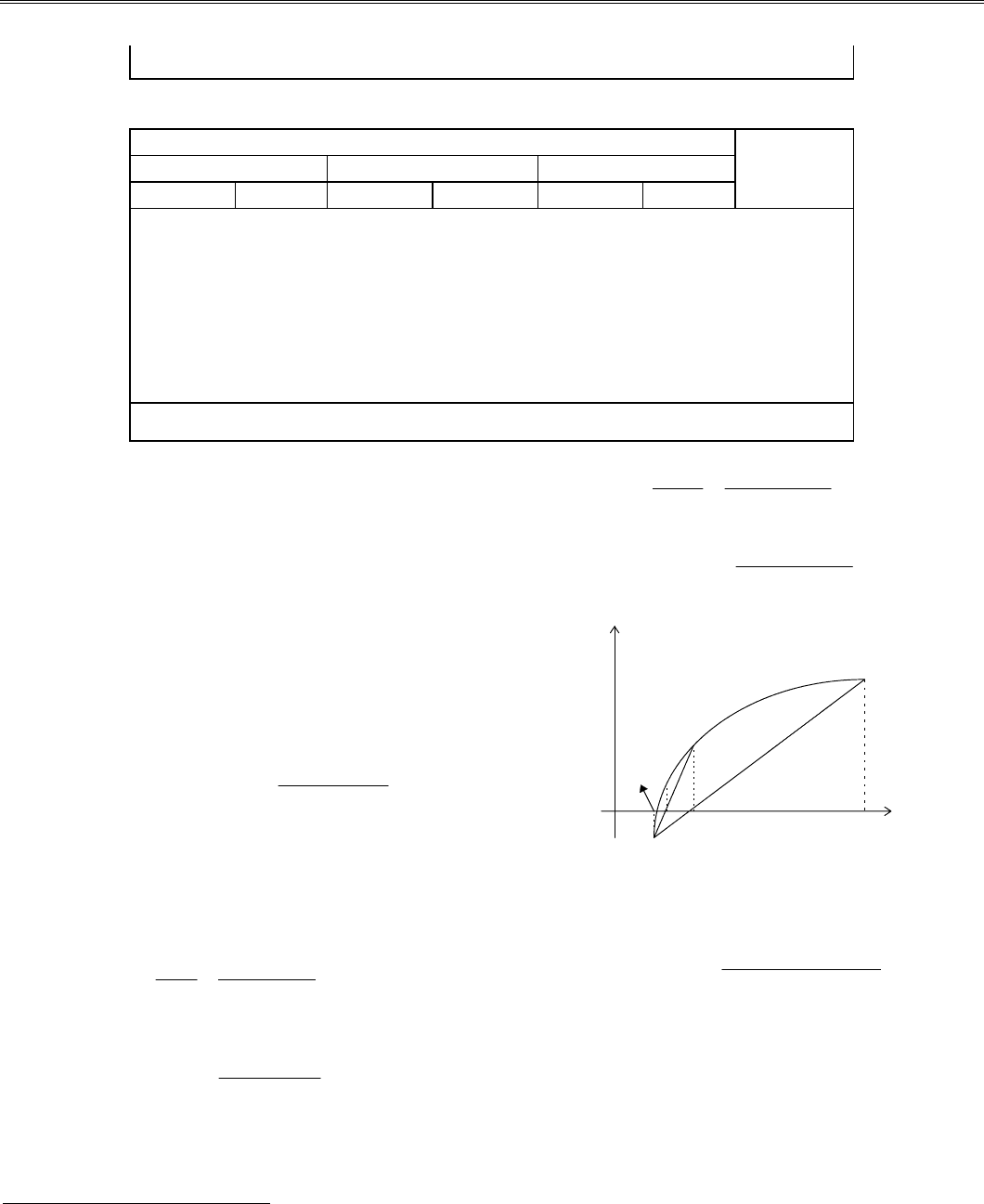
= а. Геометрически этот способ

эквивалентен замене кривой F(х) хордой А

В, проходящей

через A

(b, F(b)) и В(а, F(а)) (см. рис. 1.1). Из ана-

литической геометрии найдем х

как точку пересечения

хорды А

В с осью Ох:

yfa

fb fa

−

()

() ()

полагая при этом у = 0, имеем

()

bafa

fb fa

=−

−⋅

−

()

() ()

Точку х

ищем как пересечение хорды А

В, где А

(х

F(х

)), с осью 0х (см. рис 1.1):

Если на выделенном отрезке находятся три корня функции и более или

если корни близко расположены (в пределах заданной погрешности).

yfx

fb fx

−

()

() ( )

полагая опять у = 0, имеем:

(

)

bx fx

fb fx

=−

−⋅

−

()

() ( )

Далее каждое очередное х

будем определять по фор-

муле

х b

Рис. 1.1. Графическая интерпретация метода

хорд (секущих)

(

)

bx fx

fb fx

=−

−⋅

−

−−

−

()

() ( )

. (1.17)

Процесс продолжаем до тех пор, пока не начнет вы-

полняться условие |х

- х

-1

| < ε.

Оценим погрешность этого метода [Березин, Жидков,

1962]. Пусть найдутся х

и х

-1

и пусть F'(х) непрерывна и на

всем отрезке [а, b] сохраняет свой знак, причем выполня-

ется условие:

0 < m

< |F'(х)| < М

< +7.

Примем, что х

определен по формуле (1.17), где n = 1,

2, ..., а; b - неподвижная точка. Учитывая, что F(ξ) = 0, име-

ем

§ 2. Решение нелинейных алгебраических уравнений с одной переменной

()

ffx

fx fb

() ( )ξ− =

−

⋅−

−

−1

и, применив теорему Лагранжа o конечном приращении

функции, получим:

(ξ − х

n -1

) F '(ξ

n -1

) = (х

- х

n -1

) F '(X

n -1

) ,

где ξ

n -1

∈ [x

n -1

, ξ],

n -1

∈ [x

n -1

, ξ],

следовательно

()()

()

−=

′

−

′

⋅−

−

−−

−

fX f

nn1

. (*)

Так как F '(х) сохраняет постоянный знак на отрезке [а,

b], причем ξ

n-1

∈ [x

n-1

, ξ]

и X

n-1

∈ [x

n-1

, ξ], то числитель дро-

би можно ограничить разностью между max (F'(ξ) ) и

min( F'(ξ) ) на отрезке [а, b]:

|F '(X

n-1

) - F'(ξ

n-1

)| < М

- m

. (**)

Из выражений (*) и (**) находим

ξ− ≤

−

⋅−

−

nn1

1−n

, (1.18)

где М

= sup ( |F '(х)| ) и m

= inf ( |F '(х)| ) на отрезке [а, b].

Если при этом отрезок [а, b] мал, то имеет место нера-

венство М

< m

, тогда оценка

ξ− ≤ −

−−

xxx

nnn11

еще

более упрощается, т.е., как только обнаружили, что рас-

стояние между двумя последовательно вычисленными

корнями |х

- х

n-1

| ε , где ε - заданная предельная по-

грешность, то можно гарантировать, что |ξ - х

≤

n-1

≤

ε. Для

вычисления значения корня на отрезке [а, b] с заданной

точностью ε можно воспользоваться процедурой HORD.

Формальные параметры процедуры. Входныe: а, b

(тип real) - отрезок, на котором ищется корень; ерs (тип re-

al) - точность вычисления корня; k (тип integer) - разре-

шенное число итераций; FUNC - внешняя процедура-функ-

ция. Выходные: k (тип integer) - количество выполненных

итераций; х (тип real) - найденное значение корня с задан-

ной точностью ерs.

PROCEDURE HORD (A,B,EPS:REAL; IT:INTEGER;

VAR X : REAL; VAR K:INTEGER);

VAR X1,X2,X3 : REAL; K1 : INTEGER;

BEGIN

K := 1;

X1 := FUNC(A);

X2 := FUNC(B);

X3 := B - X2*(B-A)/(X2-X1);

IF SIGN(X2)=SIGN(FUNC(X3)) THEN

K1:=1

ELSE

BEGIN

K1:=2;

X1:=X2;

END;

REPEAT

INC (K);

X := X3;

CASE K1 OF

1: X2:= X3-FUNC(X3)*(X3-A)/(FUNC(X3)-X1);

2: X2:= X3-FUNC(X3)*(B-X3)/(X1-FUNC(X3));

END;

X3 := X2;

UNTIL (K>IT) OR (ABS(X-X2)<EPS);

END.

Для проверки процедуры решалось уравнение

2 соs(х + π/6) + х

- 3х + 2 = 0.

Первоначально корни уравнения определяли с

точностью 0.1 графическим методом, а затем найденное

значение корня уточняли методом хорд до 0.0001.

Перепишем уравнение в виде

2 соs(х + π/6) = -х

+ 3х - 2 ,

и если построить два графика: у = 2 соs(х +π/6) и у = -х +

3х- - 2, то можно убедиться, что один корень ~1.1, а второй

~2.9. Поэтому первый интервал выбираем [0.9; 1.3],

второй - [2.7; 3.1]. Точность установим ε = 0.0005.

Процедура-функция может выглядеть так:

UNCTION FUNC (X :REAL) : REAL;

BEGIN FUNC := X*X - 3*X +2.0 + 2.0*COS(X+PI/6);

END.

Результаты расчетов с использованием подпрограммы

HORD приводятся в табл. 1.6.

Таблица 1.6

Первый корень на интервале [0.9; 1.3] Второй корень на интервале [2.7; 3.1]

i +1

№ итерации x

i+1

№ итерации

1.044879

1.032336

1.031823

1.031803

1.032336;

1.031823;

1.031803;

1.031802;

k = 1

k = 2

k = 3

k = 4

2.915101

2.953624

2.959635

2.960551

2.960690

2.960711

2.953624;

2.959635;

2.960551;

2.960690;

2.960711;

2.960714;

k = 1

k = 2

k = 3

k = 4

k = 5

k = 6

x = 1.031803; F(x) = — 0.0000025773; k = 4 x = 2.960711; F(x) = — 0.0000135768; k = 6

Глава 1. Численные методы алгебры

2.3. ПРИБЛИЖЕННОЕ РЕШЕНИЕ

УРАВНЕНИЯ F(х) = 0

МЕТОДОМ КАСАТЕЛЬНЫХ (Ньютона)

Если известно начальное приближение решения урав-

нения F(х) = 0 на отрезке [а, b], то уточнить корень можно,

как уже говорилось, любым способом. Одним из самых

эффективных и точных решений является метод Ньютона

(метод касательных), который состоит в построении итера-

ционной последовательности [Бахвалов, 1973б]

xxFxFx

nn n+

=−

′

() ()

сходящейся к корню уравнения F(ξ) = 0. Для применения

этого метода необходимо существование первой и второй

производных и их знакопостоянство на исследуемом отре-

зке.

Рассмотрим метод более подробно. Пусть найдено не-

которое = ξ, где ξ ∈ [а, b]. При уточнении корня по ме-

тоду Ньютона полагаем ξ = , где - достаточно

малое число. Тогда, считая ξ корнем уравнения, находим ,

применив формулу Тейлора:

+ h

0 ==+

′

FFxhFxhFx

nn n n n

() ( ( ( )

) = ) +

откуда

hFxFx

=−

′

() ( )

, и окончательно получаем ре-

куррентную формулу

=−

′

−

()

. (1.19)

Достаточные условия сходимости определяются теоремой.

Теорема: Пусть F(х) определена и дважды дифферен-

цируема на отрезке [а, b], причем F(а)F(b) < 0, а производ-

ные F'(х) и F"(х) сохраняют знак на отрезке [а, b]. Тогда,

исходя из начального приближения х

∈ [а, b], удовлетво-

ряющего неравенству F'(х

)F"(х

) > 0, можно построить

последовательность

xxFxFx

nn n+

=−

′

() ()

, n = 0, 1, ...,

сходящуюся к единственному на отрезке [а, b] решению ξ

уравнения F(ξ) = 0.

Если нулевое приближение выбрано достаточно близко

к корню, то итерации сходятся очень быстро, со ско-

ростью геометрической прогрессии.

Алгоритм данного метода очень простой и ясный и

имеет, как и метод хорд, графическую интерпретацию

(рис. 1.2).

1. Через точку А

(х, у) с координатами х = b, у = F(b)

проводим касательную.

2. Находим пересечение касательной с осью 0x (точка х

3. Находим значение функции в точке х = х

; y = F(х

4. Проводим касательную в точке х = х

; y = F(х

) (точка

5. Находим точку пересечения касательной с осью 0х

(точку х

), и так далее до выполнения условия

−≤

−1

. За корень ξ принимаем х

F(x

)

F(b)

••

•

•••

•

Рис. 1.2.

Геометрическая интерпретация метода

касательных (Ньютона)

Для оценки погрешности n-го приближения корня

[Березин, Жидков, 1962] можно воспользоваться нера-

венством:

ξ−≤−

−

xxxM m

nnn12 2

2/( )

где М

= sup |F"(х)| на отрезке [а, b], m

= inf |F'(х)| на от-

резке [а, b]. Таким образом, если

−≤

−1

, то

ξε−≤ ⋅xM m

n 2

2/( )

Последнее неравенство означает, что при удачном началь-

ном приближении корня после каждой итерации ко-

личество верных цифр удваивается. Следовательно, про-

цесс вычисления корня можно прекратить, если

xx m M

−≤=

−12

2εε/

Заметим еще раз, что метод Ньютона эффективен, если

выбрано хорошее начальное приближение корня и график

функции имеет большую крутизну в окрестности корня. В

этом случае процесс быстро сходится. Если же численное

значение F'(х) вблизи корня мало, т.е. график почти парал-

лелен оси 0х, то процесс вычисления корня будет долгим и

ошибки округления чисел в машине могут вызвать обрат-

ный процесс - решение начнет расходиться. В этом случае

можно посоветовать воспользоваться для уточнения корня

другими более эффективными методами.

Алгоритм решения задачи достаточно простой и требу-

ет особых пояснений. Процедура NEWTON вычисления

приближенного значения корня уравнения F(х) = 0 мето-

дом Ньютона (касательных) по формуле (1.19) приводится

ниже. Она была написана на языке FORTRAN, [Плис, Сли-

вина, 1983] и переведена авторами на язык PASCAL.

Формальные параметры процедуры. Входные: x0

(тип real) - начальное приближение; n (тип integer) - мак-

симально допустимое количество итераций; eps (тип real)

- значение ε в условии окончания итерационного про-

цесса; func - имя внешней подпрограммы-функции (тип

real), по которой вычисляется значение функции F(х);