Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

17.2 Dynamical simulations 581

0.3c

X / M X / MX / M

Y / MY / M

t = 0.00 M

t = 126 M

t = 151 M

t = 185 M

t = 60.4 M

t = 106 M

−5

0.3c

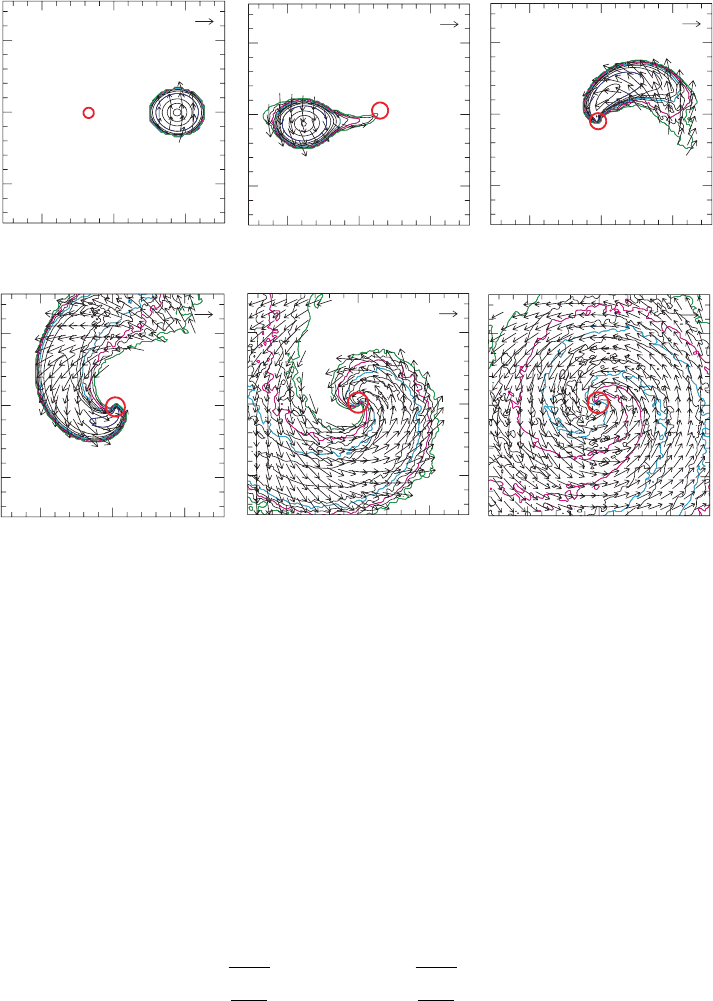
Figure 17.6 Snapshots of rest-density contours and 3-velocity vectors at selected times during the binary

merger of a 1.3M



neutron star corotating about a 3.2M



nonspinning black hole. The total initial ADM mass of

the system is M = 4.5M



. Contours are drawn in the orbital plane at ρ

= 10

(blue), 10

(cyan), 10

(magenta), and 10

gcm

−3

(green). The maximum density at t = 0is≈ 7.2 × 10

gcm

−3

. The thick red circle

denotes the apparent horizon. [From Shibata and Ury

u (2007).]

short-hard GRB, the merger and disruption of a neutron star with a low-mass black hole

might be the progenitor of such a source. A representative tidal disruption is illustrated in

Figure 17.6.

Gravitational waveforms for a typical merger are shown in Figure 17.7.Thewavesare

extracted from the metric near the outer boundaries of the grid, using the gauge-invariant

Moncrief formalism discussed in Chapter 9.4.1. In particular, Shibata and Ury

u (2006,

2007) focus on the dominant even-parity, l = 2 mass quadrupole modes and deﬁne the

quantities

)

16π

22+

, R

)

16π

22−

, (17.29)

where R

lm±

are the even-parity functions deﬁned in equations (9.117).

Exercise 17.5 Why do the functions R

21±

vanish for these simulations?

582 Chapter 17 Binary black hole–neutron stars

0.2

0.1

−0.1

0.1

−0.1

−0.2

0.2

R× / M

+ / M

50 100 150 200

ret

/ M

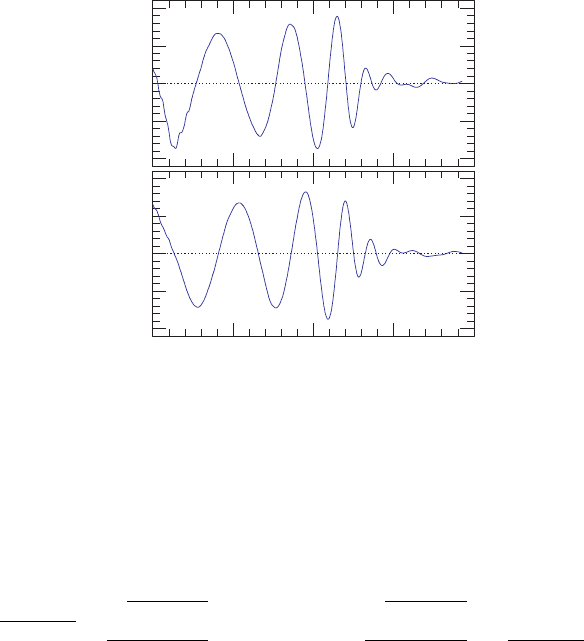
Figure 17.7 Gravitational waveforms for the binary merger of a 1.3M



neutron star corotating about a 4.0M



black hole. The total initial ADM mass of the system is M = 5.3M



(see text). [From Shibata and Ury

u (2007).]

The wave amplitude assumes its maximum for observers viewing along the binary axis,

perpendicular to the orbital plane, for which we may write

h ≡



+ h



+ R

≈ 1.0 × 10

−22







+ R

0.31 km







100 Mpc



(17.30)

where D is the distance of the observer to the source.

Exercise 17.6 Verify equation (17.30).

Hint: Use equations (9.115)and(9.116).

From Figure 17.7, which applies to a system with total mass M ≈ 5.3M



, this maximum

amplitude is h ≈ 5 × 10

−22

for a characteristic distance of D = 100 Mpc. Such a waveform

should be detectable by a gravitational wave laser interferometer like advanced LIGO. The

waveform exhibits the characteristic increase in amplitude and frequency during the late

inspiral phase, t

ret

≡ t − D

∼

120M. At the end of the inspiral the wavelength of the

radiation is ∼25M, appropriate for orbital motion near the ISCO. For 120

∼

ret

∼

150,

black hole ringdown radiation is evident, with an expected quasinormal wavelength of

∼15M

, where the ﬁnal black hole mass M

is comparable to the total initial mass of

the binary.

17.2 Dynamical simulations 583

Irrotational binaries

The merger of irrotational binaries (irrotational neutron stars orbiting nonspinning black

holes) has been treated by several investigators in full general relativity.

The emphasis has

been on low-mass cases (q

∼

5) for which the neutron star undergoes tidal disruption prior

to capture. In most of these investigations, the gravitational ﬁelds are evolved by the BSSN

scheme, and the matter is evolved by a HRSC algorithm on the same spacetime lattice.

By contrast, Duez et al. (2008) evolve Einstein’s equations by a ﬁrst-order representation

of the generalized harmonic formulation using pseudo-spectral methods. The equations of

hydrodynamics are evolved on a separate grid using shock-capturing ﬁnite difference or

ﬁnite volume techniques. The consensus of all the studies is that a toroidal disk forms

around the black hole in most cases but that the typical disk masses are much lower than

the values quoted in the previous sections. In the following discussion we shall highlight

the calculations of Etienne et al. (2009), in part to facilitate a comparison in the next section

with spinning black holes, which they also treat. For irrotational binaries, Etienne et al.

(2009) ﬁnd that, though indeed lower, the disk masses of 0.01–0.05M



that form around the

remnant black hole following neutron star disruption are still astrophysically signiﬁcant.

The code developed by Etienne et al. (2009) is a reﬁnement of the BSSN HRSC

relativistic MHD scheme of Duez et al. (2005b) discussed earlier in the book in several

other contexts.

Their most signiﬁcant improvement consists of the implementation of

AMR

to track the evolution of the strong-ﬁeld, inner regions at high resolution while

simultaneously allowing the grid to extend far out into the wave zone for more accurate

wave extraction and more reliable boundary conditions. Etienne et al. (2009) launched

a new suite of tests to check the AMR version of their code. These tests involved both

vacuum spacetimes and spacetimes with hydrodynamic matter sources and included shock-

tube tests and simulations of linear gravitational waves, single stationary and boosted

puncture black holes, puncture black hole binary mergers,

rapidly and differentially

rotating equilibrium stars, and relativistic Bondi accretion onto a Schwarzschild black hole.

Convergence tests performed in all cases conﬁrmed the reliability of the AMR version.

The BSSN equations are integrated with fourth-order accurate, centered, ﬁnite-

differencing stencils, except on shift advection terms, where fourth-order accurate upwind

stencils are used. Outgoing wave boundary conditions are adopted for all BSSN ﬁelds.

Fourth-order Runge–Kutta time-stepping is managed by a MoL (Method of Lines) routine,

with a Courant–Friedrichs–Lewy factor set to 0.45.

Etienne et al. (2009) ﬁnd that in the

presence of hydrodynamic matter, the evolution of the conformal variable φ rather than

See, e.g., Shibata and Taniguchi (2007); Etienne et al. (2008); Yamamoto et al. (2008); Duez et al. (2008); Etienne

et al. (2009).

See, e.g., Chapters 5.2.4, 14.2.3,and16.3.

The implementation uses the moving-box AMR infrastructure provided by the “Carpet” algorithm; see Schnetter et al.

(2004) for a description of the FMR version of the AMR algorithm and http://www.carpetcode.org for

publically available modules of the AMR version.

See Appendix I, where these simulations of binary black hole mergers are summarized, together with some of the

features of the vacuum sector of this AMR code.

See Chapter 6 for a discussion of these concepts.

584 Chapter 17 Binary black hole–neutron stars

χ = e

−4φ

or W = e

−2φ

yields a more stable evolution near the black hole puncture and

better rest-mass conservation.

The equations are evolved using standard puncture gauge

conditions: an advective “1+log” slicing condition for the lapse and a “Gamma-driver”

condition for the shift.

The HRSC scheme for the hydrodynamics is second-order accurate for laminar ﬂow,

but ﬁrst-order accurate when discontinuities like shocks arise. To stabilize the scheme in

vacuum regions, a tenuous atmosphere is maintained, with a density ﬂoor ρ

atm

set equal to

−10

times the initial maximum density on the grid.

Etienne et al. (2009) consider irrotational binaries with mass ratios q = 1, 3 and 5. For

initial data they use the quasiequilibrium models constructed using the conformal thin-

sandwich method in Taniguchi et al. (2008). All three cases are tracked from approximately

the same starting value of M,where is the orbital angular velocity and M is the total

ADM mass. The black hole interiors are excised in this method, but with suitable care these

regions can be ﬁlled with smooth, but otherwise arbitrary, constraint-violating “junk” initial

data that does not affect the black hole exterior when evolved.

The neutron stars obey

an n = 1 polytropic EOS initially and evolve accordingly to a  = 2 adiabatic EOS. All

neutron stars in this study have the same nondimensional rest mass,

= 0.15, which is

83% of the maximum rest mass of a nonrotating star built with the same polytropic EOS;

the compaction of the adopted neutron star is

C = 0.145 in isolation.

The q = 3 case (case A) represents a generic tidal disruption scenario. Evolution starts

from a binary coordinate separation of D

/M =8.81, corresponding to M = 0.0333.

The AMR grid used in this case has nine levels of reﬁnement; there are two sets of nested

reﬁnement boxes, one centered on the black hole and the other on the neutron star. The

maximum resolution (minimum spacing) is M/32.5 in the innermost box centered on the

black hole. Approximately 41 grid points cover the diameter of the (spherical) apparent

horizon initially and 85 grid points cover the (smallest) diameter of the neutron star. The

outer boundary of the grid is located at r/M = 197.

Figure 17.8 shows the inspiral trajectories of the black hole and neutron star while

Figure 17.9 shows snapshots of the density and velocity vectors at selected times during

the evolution for the q = 3 case. Note that the equilibrium shape of the neutron star is

hardly disturbed for the ﬁrst two orbits (upper middle). The lower panels show how the

neutron star tail deforms into a quasistationary disk, as the bulk of the matter is accreted

onto the black hole. A time history of the rest-mass consumption by the black hole is plotted

in Figure 17.10 for this case, as well as for the irrotational q = 1 (case E) and 5 (case D)

mergers. Astrophysically, we expect that the formation of a binary black hole–neutron star

will typically occur with q > 1.

Figure 17.10 suggests that for q = 3andq = 1 there are two distinct phases during

which matter falls into the black hole following tidal disruption of the neutron star: an

In contrast to evolution on a ﬁxed grid using a conservative HRSC scheme, rest-mass conservation is not guaranteed

on an AMR grid, where spatial and temporal prelongation (interpolation) is performed at the grid boundaries.

See equations (4.51)and (4.83), implementing the “shifting shift” version in the later case.

Etienne et al. (2007); see also Brown et al. (2007).

17.2 Dynamical simulations 585

−2

−4

−6

−8

−8 −6 −4 −2

2468

X / M

Y / M

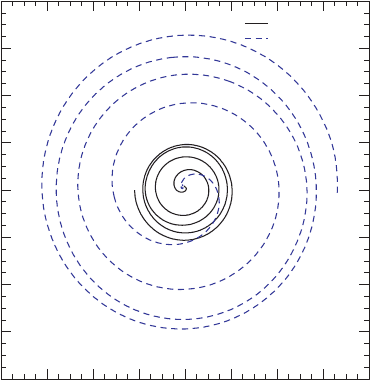
Figure 17.8 Trajectories of the black hole and neutron star coordinate centroids for the merger of an irrotational

binary with mass ratio q = 3 (case A). The black hole (BH) centroid corresponds to the centroid of the apparent

horizon, and the neutron star (NS) centroid is computed via the integral

≡ (



∗

x)/(



∗

x), where

V is the total simulation volume. [From Etienne et al. (2009).]

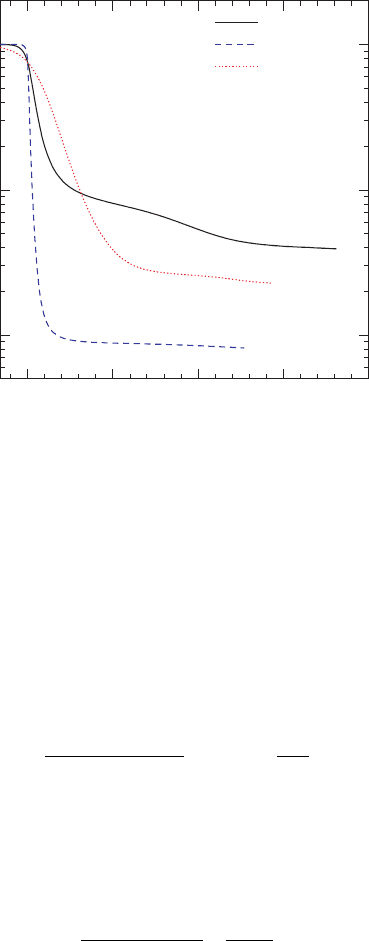
initial plunge phase and a secondary accretion phase. The plunge phase occurs early in

the merger as part of the disrupted star streams onto the black hole and the remainder

deforms into a tidal tail. The plunge phase ends after 70–90% of the matter falls into

the BH, resulting in a sudden drop in the slope of the exterior M

vs. time plot in the

ﬁgure. The debris in the tail, having larger speciﬁc angular momentum, spreads out and

forms a disk. Material with lower speciﬁc angular momentum in the disk accretes onto the

BH. Since there is neither viscosity nor magnetic ﬁelds in this simulation, the accretion

should eventually cease as the evolution continues. However, in realistic astrophysical

environments, viscosity and magnetic ﬁelds frozen into the initial gas will drive further

accretion on secular time scales.

For the q = 5 case plotted in Figure 17.10 the neutron star essentially plunges into hole,

leaving < 1% of its rest mass outside the horizen at the end of the simulation. This result

is not surprising since, at the ISCO, the tidal effect of the black hole is smaller for larger q,

resulting in tidal disruption occurring closer to the ISCO. Moreover, for a given neutron star,

the horizon size of the black hole is larger for larger q, making it easier to capture neutron

star matter during the plunge. More surprising is the result that the disk mass in the q = 1

case (M

disk

≈ 2.3%) is less than the disk mass in the q = 3 case (M

disk

≈ 3.9%).

This result is presumably due to the complicated interaction of the disrupted matter in the

Recall the examples of viscous and MHD disk accretion onto black holes discussed in Chapter 14.2.4 and 14.2.5.

586 Chapter 17 Binary black hole–neutron stars

t = 0.0M

t = 524.0M t = 550.6M t = 869.2M

Case A

0.5c

Case A

0.5c

−5

−10

−5

0510

X / M X / M X / M

Y / M

−5

−10

−5

0510

Y / M

−5

−10

−5

0510

Y / M

−5

−10

−5

0510

Y / M

−5

−10

−5

0510

t = 324.0M

t = 460.3M

Case A

0.5c

Case A

0.5c

−5

−10

−5

0510

−5

−10

−5

0510

Figure 17.9 Snapshots of rest-density contours and 3-velocity vectors at selected times during the merger of the

irrotational black hole-neutron star binary with mass ratio q = 3 shown in Figure 17.8 (case A). The contours

represent the density in the orbital plane, plotted according to ρ

= ρ

0,max

−0.38 j−0.04

, ( j = 0, 1,...,12), with

darker gray scaling for higher density. The maximum initial neutron star density is Kρ

0,max

= 0.126, where K is

the initial polytropic gas constant, or ρ

0,max

= 9 × 10

gcm

−3

(1.4M



)

. Arrows represent the velocity ﬁeld

in the orbital plane. The apparent horizon interior is marked by a ﬁlled black circle. In cgs units, the initial ADM

mass for this case is M = 2.5 × 10

−5

/1.4M



)s= 7.6(M

/1.4M



) km. [From Etienne et al. (2009).]

merging process. A low-density, hot spiral region of disrupted matter winds around the

black hole and smashes into the tidal tail of the disrupted star, causing signiﬁcant shock

heating. As shown in exercise 17.7 the degree of shock heating can be considerable in a

supersonic, low-density stream. Some of the heated matter transfers angular momentum to

the other part of the tail and then falls into the black hole. The remaining matter in the tail

deforms into an inhomogeneous disk before settling into a quasistationary state in which

a high density, relatively low temperature torus of matter surrounds the black hole.

Exercise 17.7 Shock heating can be measured by the degree to which the polytropic

gas constant K ≡ P/ρ



increases in a gas that passes through a shock front. Recall

that this quantity remains constant for adiabatic ﬂow in the absence of shocks.

Assume Newtonian hydrodynamics in doing this exercise.

17.2 Dynamical simulations 587

0.01

0.1

Case A

Case D

Case E

100 200

3:1 = M

1:1

5:1

300 400

(t − t

) / M

Fraction Outside AH

Figure 17.10 Rest-mass fraction outside the black hole as a function of time for irrotational binaries with

different mass ratios. Here, the time coordinate is shifted by t

, the time at which 25% of the neutron star

rest-mass has fallen into the apparent horizon. [From Etienne et al. (2009).]

(a) Assume that matter evolves adiabatically with the same adiabatic constant >1

both before and after entering a planar shock front. Let the upstream Mach number

in a ﬂuid entering a shock be deﬁned by

M ≡ v

,wherev

is the upstream ﬂow

as viewed in the frame of the shock front and c

is the upstream sound speed. Use

the fact that the ﬂow always enters a shock front supersonically (i.e.,

M > 1) to

show that the downstream-to-upstream ratio of the gas constants is given by

2

− ( − 1)

( + 1)

+1



 − 1 +





. (17.31)

Prove that this ratio is always larger than unity.

(b) Evaluate

M in terms of v

and ρ

and argue that for a given upstream velocity,

M is larger for a lower density ﬂuid.

M  1andshowthat

≈

( + 1)K

−1



 − 1

 + 1





. (17.32)

Equation (17.32) shows that when the density ρ

of the upstream matter is low, the

degree of shock heating downstream can be substantial, i.e., K

 1.

Etienne et al. (2009) ﬁnd that the disk is smallest and most dense for the q = 1

binary. Specifying the length scale in km via the relation M = 1.9(q + 1)(M

/1.4M



)km,

and setting the neutron star rest mass M

equal to 1.4M



, they obtain a characteristic

588 Chapter 17 Binary black hole–neutron stars

radius of r

disk

≈ 20 km and a maximum density of ρ

0,max

≈ 6 × 10

gcm

−3

for this

disk. The corresponding values for the disk in the q = 3 case are r

disk

≈ 50 km and

0,max

≈ 4 × 10

gcm

−3

. In all cases the disk forms a hot, thick torus whose height is

about 15–20% of the characteristic radius and whose density plummets at the black hole

ISCO. The low-density regions are hottest, due to shock heating (see exercise 17.7). How-

ever, the gas constant K ≡ P/ρ



increases by more than a factor of 6 everywhere in the

q = 1 disk and by more than 85 everywhere in the q = 3disk.

Etienne et al. (2009) determine the thermal temperature T in the gas from the speciﬁc

energy density , which can determined from the evolved hydrodynamic variables. For a

polytropic equation of state, the “cold” contribution 

cold

is deﬁned as



cold

=−



cold

d(1/ρ

) =

cold

 − 1

−1

, (17.33)

where P

cold

≡ K

cold



governs the initial (cold) neutron star. Now deﬁne the thermal

contribution to the speciﬁc energy density generated by shock heating as 

=  − 

cold

and compute the thermal contribution according to



=  − 

cold

 − 1

−

cold

 − 1

−1

= (K /K

cold

− 1)

cold

. (17.34)

To estimate T , Etienne et al. (2009) model 

according to



3kT

+ f

, (17.35)

where m

is the mass of a nucleon, k is the Boltzmann constant, and a is the radiation

constant. The ﬁrst term represents the approximate thermal energy of the nucleons, and the

second term accounts for the thermal energy due to radiation and (thermal) relativistic parti-

cles. The factor f

reﬂects the number of species of ultrarelativistic particles that contribute

to thermal energy. When T  2m

/k ∼ 10

K, where m

is the mass of electron, thermal

energy is dominated by photons and f

= 1. When T  2m

/k, electrons and positrons

become ultrarelativistic and also contribute to the energy, and f

= 1 + 2 × (7/8) = 11/4.

At sufﬁciently high temperatures and densities (T

∼

K, ρ

∼

gcm

−3

), thermal

neutrinos are copiously generated and become trapped, so, taking into account three ﬂavors

of neutrinos and antineutrinos, f

= 11/4 + 6 × (7/8) = 8.

Using equation (17.35), the characteristic temperature is T ∼ 5 × 10

K(or∼4MeV)

in the disk formed following the q = 3 binary merger, with comparable values for the

other disks. Numerical models of rotating black holes with ambient disks with similar

temperatures and densities suggest that such systems can produce a total gamma-ray energy

E ∼ 10

–10

erg from neutrino-antineutrino annihilation.

This result is promising for

generating a short-hard GRB from a merging black hole–neutron star binary.

Setiawan et al. (2006).

17.2 Dynamical simulations 589

0.15

0 100

150

Case E

Case A

Case D

200 300

300

(t − r

) /M

/ M)h

/M)h

450

600

−0.15

0.15

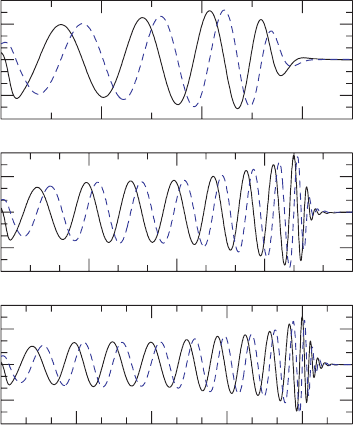
Figure 17.11 Gravitational wave signal for irrotational binaries with mass ratios (top to bottom) q = 1, 3, and

5. The black solid (blue dash) line denotes the (2,2) mode of h

) extracted at r

= 43.4M.[FromEtienne

et al. (2009).]

Gravitational waveforms are computed for the three cases described above and the results

are compared in Figure 17.11. Waveforms extracted at different radii are found to overlap

well provided the extraction radius is sufﬁciently large: r

∼

40M. With approximately the

same initial M, we observe more wave cycles are emitted as the mass ratio q is decreased.

The amplitudes are attenuated at frequencies roughly equal to double the orbital frequency

at which tidal disruption begins.

Exercise 17.8 The gravitational waveforms h

and h

can be decomposed into

s =−2 spin-weighted spherical harmonics

−2

according to

− ih



l,m

− ih

)

−2

, (17.36)

where h

and h

are real functions. Each (l, m) mode is a function of radius and

time only.

(a) Use the results of Chapter 9.4 to express h

and h

in terms of gauge-invariant

Moncrief functions.

(b) Use the results of Chapter 9.4 to express h

and h

in terms of the Weyl scalar

One signiﬁcant measure of the accuracy of the simulations is provided by the degree to

which energy and angular momentum are conserved. Etienne et al. (2009) calculate the

590 Chapter 17 Binary black hole–neutron stars

diagnostic quantities

δE ≡ M − M

− E

, (17.37)

δ J ≡ J − J

− J

, (17.38)

where M and J are the ADM mass and angular momentum of the initial binary, M

and

are the ADM mass and angular momentum of the ﬁnal system, and E

and J

are the energy and angular momentum carried off by gravitational waves. Assuming that

no matter or other form of radiation leaves the computational domain, which is the case

here, strict conservation of energy and angular momentum demands that δ E = 0 = δ J .

Etienne et al. (2009) ﬁnd that (δ E/M,δJ/J ) = (−2 × 10

−4

, 2.2 × 10

−2

) for the q = 3

case, which takes approximately 4.5 orbits before merger, with comparable errors for the

other cases. Maintaining conservation of angular momentum is typically more difﬁcult

than energy conservation, due to spurious numerical viscosity (shear) effects. Moreover,

the determination of the ﬁnal disk mass is particularly sensitive to errors in angular

momentum conservation, so they must be kept to a minimum (

∼

a couple percent) for a

reliable measure.

The radiated fractions (E

/M,J

/J ) are found to be (0.35%, 7.2%) for the

q = 1 system, (0.93%, 17.4%) for q = 3, and (0.98%, 19.2%) for q = 5. The spins J

of the black hole remnants are 0.85 for q = 1, 0.56 for q = 3 and 0.42 for q = 5. Binary

black hole–neutron star mergers typically impart kick velocities to the remnant black holes

due to recoil.

The kick velocity v

kick

is calculated to be 17 km/s for q = 1, 33 km/s for

q = 3 and 73 km/s for q = 5.

By evolving initial binaries along the same quasiequilibrium sequences as those cho-

sen here but with larger initial separations (smaller M) Etienne et al. (2009)ﬁndthat

the outcomes (apart from a phase shift in the case of gravitational waves) are essen-

tially unchanged. This indicates that choosing the initial separation corresponding to

M = 0.0333 is sufﬁciently large to predict the onset of tidal disruption, merger evolu-

tion, gravitational waveforms and disk masses reliably, although this result may only be

marginally true in the case of q = 1(seeexercise17.9).

Exercise 17.9 Explain why ﬁxing the initial value of M leads to closer initial sep-

arations as the binary mass ratio q is decreased. Speciﬁcally, estimate the separation

in a circular binary as a function of M and q.

Figure 17.12 plots the gravitational wave power spectra (i.e., the effective wave strain

eff

( f ) ≡ (

√

2/π D)(

√

dE/df) vs. f ,whereE( f ) is the Fourier transform of the energy, f

the frequency and D the source distance) for the three cases, using only the dominant (2,2)

and (2,−2) wave modes, and compares them to the Advanced LIGO sensitivity curve,

or effective strain, h

LIGO

( f ) ≡

√

( f ).

To set the scale in the ﬁgure, the neutron

See Chapter 13.2.2 for a discussion of recoil in the context of binary black hole mergers.

The quantity h

LIGO

( f ) is related to the LIGO “strain per root hertz”, or noise,

h( f ) plotted in Figure 9.4 by

LIGO

( f ) =

h( f )

√

f .