Басенко В.Г., Гуменюк В.И., Танчук М.И. Безопасность жизнедеятельности. Защита в чрезвычайных ситуациях

Подождите немного. Документ загружается.

111

ляет оценить последствия по типу «поражен – не поражен»: при

пор

JJ ≥

–

объект поражен, при

пор

JJ <

– не поражен.

У человека болезненные ощущения возникают при повышении тем-

пературы поверхностного слоя кожного покрова до 45 ºС. Интенсивности

теплового излучения и время воздействия, вызывающие различную реак-

цию при облучении незащищенных кожных покровов человека, приведены

в табл. 2.1. Пороговым значением в аварийной ситуации считают

пор

4,2 кВт/м

, поскольку при этом болевая реакция наступает относительно

медленно и есть возможность принять меры защиты – удалиться от источ-

ника облучения или использовать экран – неровности поверхности земли,

строения, инженерные сооружения.

Воздействие теплового излучения на материалы может привести к их

возгоранию. Интенсивности теплового излучения и время, при которых

происходит возгорание материалов, приведено в

таблице 2.2.

Т а б л и ц а 2.1

Действие теплового излучения на человека

Наблюдаемый эффект Интенсивность излучения,

кВт/м

Переносится длительное время 1,26*

Болевые ощущения через 10…20 с 4,2

Болевые ощущения через 8 с 6,4

Болевые ощущения через 3 с 10,4

Появление ожогов (волдырей) через 10…20 с 10,4

Появление ожогов (волдырей) через 5 с 16

Примечание. * Интенсивность полного теплового излучения Солнца в зените на

поверхности Земли с учетом поглощения составляет 1,05 кВт/м

Использование в детерминированном методе прогнозирования поро-

говых интенсивностей

пор

для различных длительностей воздействия

позволяет приближенно учесть совместное влияние этих параметров на

получаемый результат.

Для пожара огневой загрузки и в некоторых случаях – для пожара

разлития данные табл. 2.1, 2.2 позволяют рассчитать расстояния безопас-

ного удаления человека и горючих материалов от горящего объекта.

112

Т а б л и ц а 2.2

Минимальные интенсивности теплового излучения и время, при

котором происходит возгорание горючих материалов, кВт/м

Материал Продолжительность действия, мин.

3 5 15

Древесина (сосна влажность 12 %) 18,8 16,9 13,9

Древесно-стружечная плита 13,9 11,9 8,3

Торф брикетный 31,5 24,4 13,2

Торф кусковой 16,6 14,4 9,8

Хлопок – волокно 11,0 9,7 7,5

Слоистый пластик 21,0 19,1 15,4

Стеклопластик 19,4 18,6 17,4

Пергамин 22,0 19,8 17,4

Резина 22,6 19,2 14,8

Уголь - 35,0 35,0

Результаты, достаточно хорошо согласующиеся с опытными данны-

ми, можно получить, используя теорию теплового излучения. Если

–

площадь излучающей поверхности, то интен-

сивность облучения площадки

(рис. 2.3)

может быть определена на основании закона

Стефана-Больцмана для теплового излучения

абсолютно черного тела

σ= , где

–

энергетическая светимость (интегральная из-

лучательная способность) пламени, Вт/м

;

1067,5

−

⋅=σ

Вт/(м

·К

) – постоянная Стефана-Больцмана;

– термоди-

намическая температура, К.

Экспериментально получены значения энергетической светимости

, учитывающие температуру горения и отличие излучателя от абсолют-

но черного тела (среднеповерхностная плотность теплового излучения

пламени), которые рекомендуется использовать при расчетах:

=40 кВт/м

– для твердых материалов и нефтепродуктов,

=120 кВт/м

– для сжиженных углеводородных газов,

= 450 кВт/м

–

для пожара огненный шар.

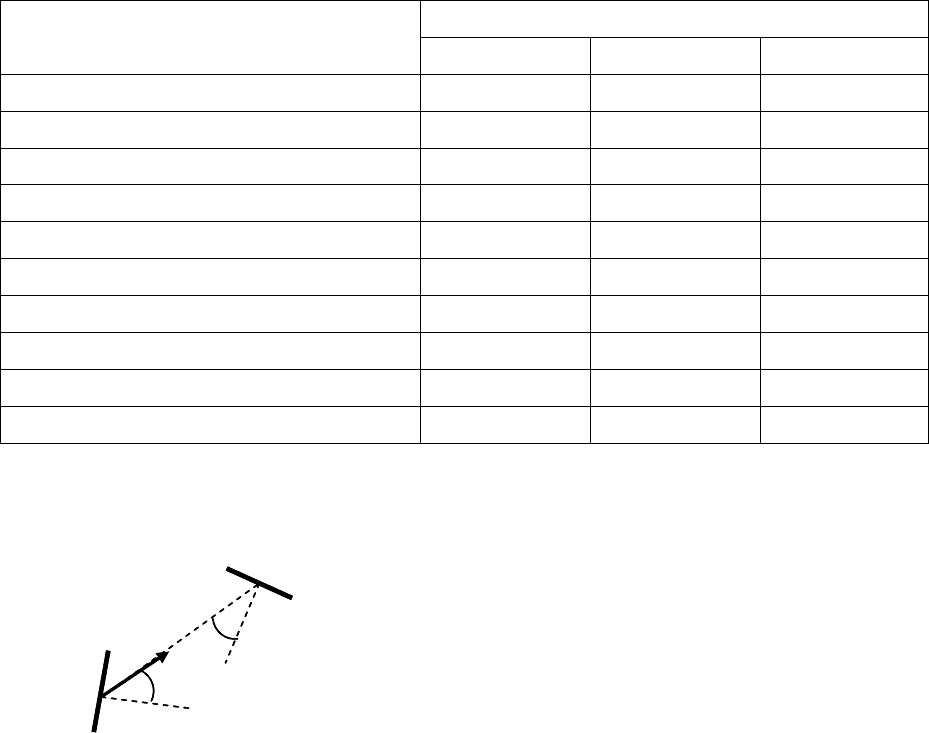
Рис. 2.3. Схема облучения

поверхности

Рис. 2.3. Схема облучения

поверхности

113

При оценочных расчетах полагаем, что геометрия задачи соответст-

вует точечному тепловому источнику с температурой

, излучающему в

полуплоскость, а также:

=ϕ

, и

TT >>

. Тогда интенсивность теп-

лового потока на облучаемом объекте определяется выражением:

= ,

(2.1)

где

– площадь поверхности излучателя (пламени), обращенной к объек-

ту, м

;

– расстояние от источника теплового излучения до объекта, м.

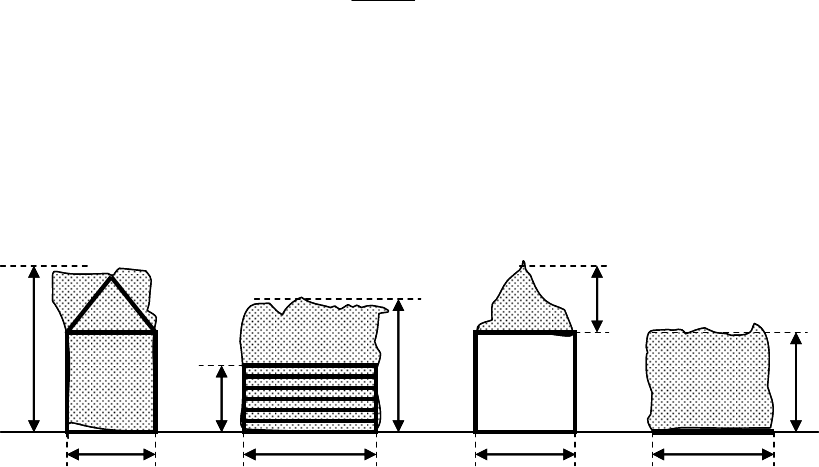
Площадь излучающей поверхности – факела пламени

при безвет-

рии приближенно может быть определена в соответствии с рис. 2.4 сле-

дующим образом.

При горении здания, штабеля леса и им подобных объектов (рис.

2.4–а, б)

abF =

, где a – длина здания или длина штабеля,

– высота от

поверхности земли до конька крыши; для штабеля

штшт

hhb ,)5,33( −

–

высота штабеля. При горении горючих жидкостей в открытом резервуаре

(рис. 2.4–в)

– площадь равнобедренного треугольника с основанием,

равным диаметру резервуара

и высотой

d)5,12,1(

−

. При горении

жидкости, разлитой по поверхности земли, (рис. 2.4–г) факел пламени

представляется цилиндром, излучающая поверхность – прямоугольник с

основанием, равным диаметру пятна

, м и высотой

7,0

5,2

dH ≈ , м.

Диаметр пятна

оценивается, исходя из условия, что толщина слоя го-

рючей жидкости на поверхности земли равна 5 см.

а) б)

в)

г)

Рис.2.4. Аппроксимация излучающей поверхности пламени различных пожаров:

а) горящий дом; б) горящий штабель лесоматериалов; в) горение жидкости в

открытом резервуаре; г) горение разлитой по поверхности жидкости.

шт

а) б)

в)

г)

Рис.2.4. Аппроксимация излучающей поверхности пламени различных пожаров:

а) горящий дом; б) горящий штабель лесоматериалов; в) горение жидкости в

открытом резервуаре; г) горение разлитой по поверхности жидкости.

шт

114

Детерминированный метод, обладая простотой и физической на-

глядностью, позволяет получить только ступенчатую оценку.

Пример 1. Определить радиус теплового поражения людей при горении

деревянного дома длиной 10 м и высотой от земли до конька крыши 15 м.

Р е ш е н и е.

Радиус поражения находим из формулы (2.1):

пор

где

= 40 кВт/м

– среднеповерхностная плотность теплового излучения пла-

мени для твердых материалов;

– площадь факела пламени

10,

== aabF

м,

15=b м;

пор

J – пороговая интенсивность теплового излучения, при которой че-

ловек через 10…20 с начинает испытывать болевые ощущения

(

пор

J 4200 Вт/м

Подставляя численные значения величин в формулу, получим:

1,15

420028,6

15101040

≈

⋅

⋅⋅⋅

м.

Пример 2. При аварии на железной дороге из цистерны разлилось и заго-

релось 60 т мазута. Оценить радиус теплового поражения людей и возможность

возгорания деревянных домов, расположенных в 40 м от места аварии.

Исходные данные:

950=ρ

кг/м

– плотность мазута;

109,37 ⋅=Q

кДж/кг

– теплота сгорания мазута;

035,0

V кг/(м

·с) – массовая скорость выгорания

мазута;

E = 40 кВт/м

– среднеповерхностная плотность теплового излучения

пламени для нефтепродуктов;

2,4

J кВт/м

– пороговая интенсивность излу-

чения для человека;

8,189,13 −=

J кВт/м

– интенсивность излучения для возго-

рания древесины (время облучения соответственно 15…3 мин.). Полагаем, что

толщина пятна мазута на поверхности земли составляет

h см, безветрие.

Р е ш е н и е.

1. Определяем диаметр пятна разлившегося мазута:

πρ

, 1,40

05,095014,3

600004

≈

⋅⋅

⋅

=d м.

2. Рассчитываем продолжительность горения мазута:

Vht /

= ,

1357035,0/05,0950

≈

⋅

с=22,6 мин.

115

3. Определяем высоту пламени:

7,0

5,2 dH ≈

1,331,405,2

7,0

≈⋅=H

м.

4. Находим радиусы теплового поражения людей и возгорания деревян-

ных домов:

9,44

420028,6

1,331,401040

≈

⋅

⋅⋅⋅

м,

7,24

1390028,6

1,331,401040

≈

⋅

⋅⋅⋅

м.

Вероятностный метод прогнозирования. Предполагается, что ха-

рактеристики излучения и типового нагреваемого объекта – случайные ве-

личины, следовательно, и ожидаемый результат воздействия теплового из-

лучения - также случайная величина. Метод позволяет рассчитать вероят-

ность определенного вида поражения – в действующих нормативных до-

кументах – вероятность летальных последствий для человека. Если обра-

титься к рис.1.11, то это вероятность поражения при

переходе через поро-

говую кривую – из области «не поражен» в область «поражен».

Вероятность летального поражения человека тепловым излучением

определяют по значению пробит-функции, рассчитываемой с помощью

формулы:

)ln(56,25,9Pr

33,1

Jt ⋅+−= ,

(2.2)

где

– эффективное время экспозиции, с;

– интенсивность теплового

излучения, действующего на человека, кВт/м

Пробит

– характеристика случайной величины – поражения, рас-

пределенная по нормальному закону, которая определяется для рассматри-

ваемого воздействия при обработке результатов данных экспериментов и

аварий на пожаровзрывоопасных объектах. Вероятность поражения

P мо-

жет быть рассчитана по значению пробит-функции по формуле:

∫

−

∞−

−

5Pr

dteP

(2.3)

Расчет функции распределения нормально распределенной случай-

ной величины обычно ведут, используя табулированную функцию инте-

грал Лапласа )(zФ :

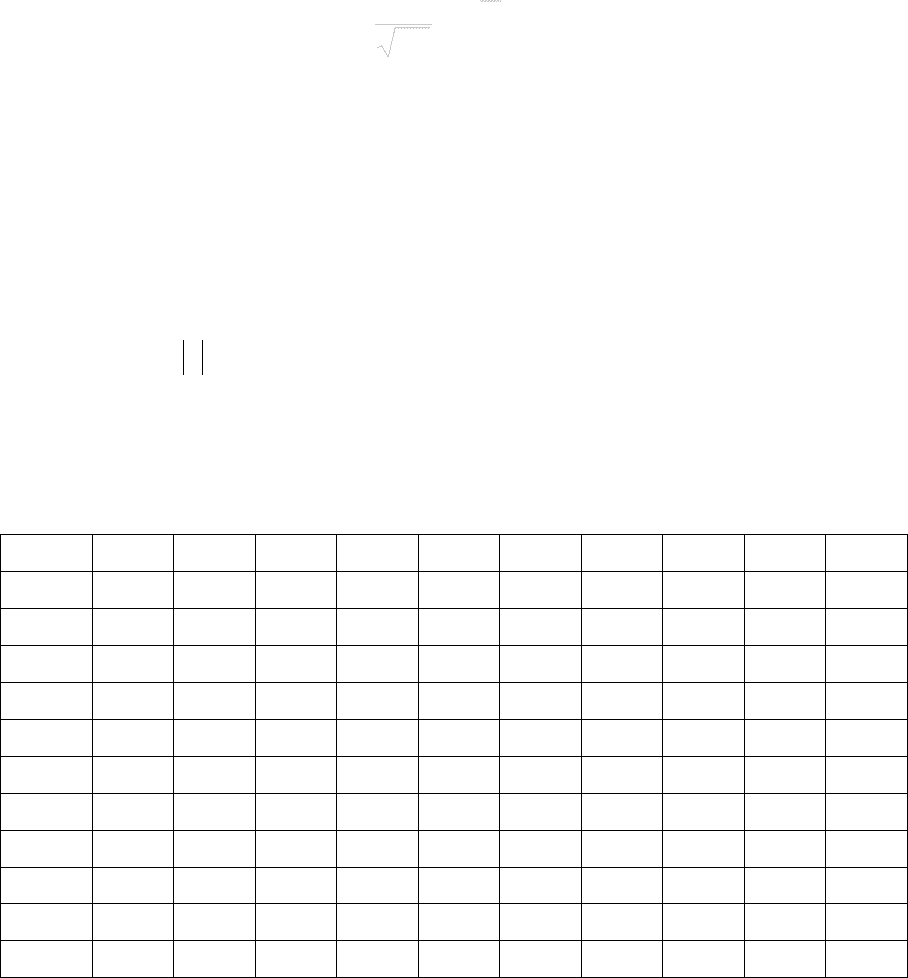
116

∫

−

dtezФ

)(

(2.4)

Тогда:

)5(P

5,0

−

= ФP

(2.5)

Для расчета интеграла Лапласа (2.4) можно воспользоваться аппрок-

симацией:

[

]

0,)8,037,0exp(15,0)()(

≥−−−=≈ zzzzФzФ

(2.6)

При

0<z

вследствие свойства нечетности

)(zФ

считаем

)()( zФzФ

аа

−=

Переход от пробит-функции к вероятности может быть осуществлен

и с помощью таблицы 2.3.

Т а б л и ц а 2.3

Значения пробит-функции

, %

0 1 2 3 4 5 6 7 8 9

0 - 2,67 2,95 3,12 3,25 3,36 3,45 3,52 3,59 3,66

10 3,72 3,77 3,82 3,87 3,92 3,96 4,01 4,05 4,08 4,12

20 4,16 4,19 4,23 4,26 4,29 4,33 4,36 4,39 4,42 4,45

30 4,48 4,50 4,53 4,56 4,59 4,61 4,64 4,67 4,69 4,72

40 4,75 4,77 4,80 4,82 4,85 4,87 4,90 4,92 4,95 4,97

50 5,00 5,03 5,05 5,08 5,10 5,13 5,15 5,18 5,20 5,23

60 5,25 5,28 5,31 5,33 5,36 5,39 5,41 5,44 5,47 5,50

70 5,52 5,55 5,58 5,61 5,64 5,67 5,71 5,74 5,77 5,82

80 5,84 5,88 5,92 5,95 5,99 6,04 6,08 6,13 6,18 6,23

90 6,28 6,34 6,41 6,48 6,55 6,64 6,75 6,88 7,05 7,33

99 7,33 7,37 7,41 7,46 7,51 7,58 7,65 7,75 7,88 8,09

В качестве примера использования вероятностного метода прогнози-

рования рассмотрим пожар огненный шар.

Интенсивность теплового излучения, входящая в (2.2), определяется

формулой:

kFEJ

⋅

(2.7)

где

– среднеповерхностная плотность теплового излучения пламени;

– угловой коэффициент облученности;

- коэффициент пропускания

117

атмосферы.

Значение

вычисляется по формуле:

[]

5,1

)/()5,0/(4

5,0/

DrDH

(2.8)

где

D – эффективный диаметр огненного шара, м;

– высота центра ог-

ненного шара, м;

– расстояние от облучаемого объекта до точки на по-

верхности земли непосредственно под центром огненного шара. Если вы-

сота центра облака неизвестна, принимают

. Тогда:

[

]

5,12

)/(14

(2.9)

Размер излучающей области

D огненного шара и время его горения

зависят от массы горючего вещества в шаре:

327,0

33,5 mD =

;

(2.10)

303,0

92,0 mt =

(2.11)

где

D – диаметр огненного шара, м;

– время его горения, с; m – масса

горючего вещества в облаке газовоздушной смеси, кг.

Коэффициент пропускания атмосферы

рассчитывается по форму-

ле:

[

]

)2/(100,7exp

224

DHrk −+⋅⋅−=

−

(2.12)

Пример 3. В результате разгерметизации трубопровода котельной в атмо-

сферу попало 350 кг метана. Определить вероятность летального поражения лю-

дей, находящихся на расстояниях 50 и 130 м от места аварии трубопровода в

случае воспламенения облака газовоздушной смеси и образовании огненного

шара.

Р е ш е н и е.

1. Рассчитываем эффективный диаметр огненного шара по

формуле (2.10):

2,3635033,5

327,0

≈⋅=D

м.

2. По формуле (2.11) определяем время горения шара:

9,535092,0

303,0

≈⋅=t

с.

3. Рассчитываем угловой коэффициент облученности для расстояний

r 50 м и =

r 130 м, полагаем высоту центра облака

1,182/ =

м:

118

[]

5,1

)/(14

[]

050,0

)2,36/50(14

5,1

≈

F ,

[]

025,0

)2,36/130(14

5,1

≈

F .

4. Рассчитываем коэффициент пропускания атмосферы:

[

]

976,0)1,181,1850(100,7exp

224

≈−+⋅⋅−=

−

[

]

924,0)1,181,18130(100,7exp

224

≈−+⋅⋅−=

−

5. Определяем интенсивность теплового излучения на расстояниях 50 и

130 м:

0,21976,0050,0450

≈

⋅

⋅=J кВт/м

, 4,10924,0025,0450

≈

⋅

J кВт/м

6. Рассчитываем пробит-функции и вероятности поражения для двух рас-

стояний:

41,5)0,219,5ln(56,25,9Pr

33,1

≈⋅+−= ,

P 66 %

02,3)4,109,5ln(56,25,9Pr

33,1

≈⋅+−= ,

P 2,4 %

2.3. ПРОГНОЗИРОВАНИЕ ПОСЛЕДСТВИЙ

ТЕХНОГЕННЫХ ВЗРЫВОВ

Оценка возможных последствий техногенных взрывов заключается в

определении размеров зон возможных поражений людей и разрушения

объектов. Для этого используются детерминированный или вероятностный

методы.

Детерминированный метод. При его использовании определяется

избыточное давление

PΔ

во фронте ударной волны на рассматриваемом

объекте, которое сравнивается с поражающим значением давления

Так производится наиболее простая – ступенчатая оценка типа “поражен –

не поражен”:

nф

PP Δ≥Δ

– объект поражен,

nф

– объект не пора-

жен. В качестве критерия поражения

обычно принимают нижний пре-

дел избыточного давления, при котором здания, сооружения, оборудова-

ние, системы электроснабжения получают средние повреждения. В целом,

считается, что большинство промышленных и жилых зданий разрушается

при избыточном давлении 25…30 кПа при внешнем воздействии и

119

20…25 кПа – при внутренних взрывах.

Более точная детерминированная оценка состояния объекта, позво-

ляющая определить материальный ущерб и средства для восстановления в

зависимости от степени его разрушения (слабые, средние, сильные, пол-

ные), может быть произведена, если имеются данные избыточных давле-

ний, вызывающих те или иные повреждения (табл. П. 2, П. 3).

Данные по степеням

разрушения объекта позволяют рассчитать ве-

роятность его поражения как функцию избыточного давления

PΔ

– т. е.

получить параметрический закон поражения

)(

. Будем считать, что

избыточное давление во фронте ВУВ, вызывающее разрушение объекта

PΔ

– случайная величина для данного типа объектов. Значение

PΔ

зави-

сит от того, с какой стороны объекта произведен взрыв, каково состояние

атмосферы, каковы индивидуальные особенности данного объекта среди

подобных и т. п. – т. е. от многих случайных факторов, интенсивность

влияния которых на величину

приблизительно одинакова. Тогда мож-

но предположить, что величина

распределена по нормальному закону

(хотя

0≥Δ

, формально считаем

∞

−

⎥

⎦

⎤

⎢

⎣

⎡

Δ−Δ

−

σπ

=Δ

)(

exp

)(

пп

(2.13)

где

PΔ – математическое ожидание поражающего избыточного давления;

σ – дисперсия случайной величины

Формальная замена левой границы диапазона поражающего избы-

точного давления с “0” на “– ∞” дает возможность использовать в даль-

нейшем табулированную функцию Лапласа.

Вероятность поражения объекта при заданном значении

PΔ

– это

вероятность того, что величина

превысит случайное значение пора-

жающего давления

PΔ

{}

∫

∞

−

ΔΔ=Δ>Δ=

пппф

PdPfPPPP )()(

(2.14)

120

Получаемая зависимость

)(

PP Δ

носит

название параметрического закона поражения

(рис. 2.5). Ошибка при замене предела интег-

рирования с “0” на “– ∞” незначительна.

Определение параметров нормального

распределения (2.13)

pп

, является само-

стоятельной сложной задачей, однако при

инженерных расчетах можно воспользоваться

выражениями (правило “трех сигм”):

maxmin

Δ+

=Δ

minmax

−

=σ

(2.15)

где

min

PΔ

– минимальное избыточное давление, определяющее нижнюю

границу слабых разрушений;

max

– максимальное избыточное давление,

определяющее верхнюю границу сильных разрушений.

Расчет вероятности поражения по формуле (2.14) удобнее проводить,

если привести распределение (2.13) к стандартному нормальному закону

)(

с параметрами 1,0

σ=

z :

пn

−

(2.16)

Тогда вероятность поражения объекта:

∫

∗

∞−

∗

−

zФdzeP )(5,0

(2.17)

где

пф

Δ−Δ

∗

∫

∗

−

∗

dzezФ

)(

– формула (2.4).

С использованием аппроксимации интеграла Лапласа (2.6) вероят-

ность поражения объекта при

пф

≥

(т. е. 0≥

∗

) определится выра-

жением:

)(5,0

∗

+= zФP

(2.18)

Если

пф

≤Δ

(т. е.

≤

∗

), то:

1,0

0,5

PΔ

Рис. 2.5. Параметрический

закон поражения

1,0

0,5

PΔ

Рис. 2.5. Параметрический

закон поражения