Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.


41
Частина 2. Початок алгебри
12
2
1
21
4
12
33 4
2
1
21
xxx
x
x
xxx
x
x
23223
22
1
21 21
xxxxxx
x
xx
231 233 0xx x xx x
45 4 5 5xx xx x
Після піднесення у квадрат одержимо
22
16 10 25 26 25 0xx x x x
1,2
13 169 25 13 144 13 12;x
1
25 5,x
2
15.x
Тому лише х
1
є розв’язком рівняння.
b) винесемо за дужки спільний множник (з меншим показником
степеня), тоді одержимо
22 2 2
5 5 3 140 5 28 140 5 5 2 1 3
xxx
xx
– це і є розв’язком рівняння.
c) цей приклад розв’яжемо шляхом введення нової змінної
30.
x
y
Тоді рівняння набуває вигляду: у
2
– 5у + 6 = 0.
Розв’язок цього квадратного рівняння відносно у буде:
1,2
5 25 5 25 24 5 1
6;
24 2 4 22
y
1
3;y
2
2.y
Тепер треба повернутися до початкової змінної х:
з рівності
1
33 1;
x
x
з рівності
23
32 log2
x
x
.
Знайдені х
1
і х
2
будуть розв’язками рівняння с).
d) рівняння
22
27
x
x
поділимо на
2
7
x
, тоді одержимо

42
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
2.3.7. Розв’язування логарифмічних рівнянь
Логарифмічними називають такі рівняння, які містять невідоме
під знаком логарифма.
При розв’язанні логарифмічних рівнянь використовують основні
властивості логарифмів:
1.
12 12
log log log
aa a
NN NN
.
2.
1
12
2
log log log
aa a
N
NN
N
.
3. log log
log log
1
4. log log
k
k
aa
n
a
a
a
a
NkN
n
x
x
k
NN
.
5.
lo
g
lo
g
bb
ca
ac
.
а також такі прийоми:
a) потенціювання: з рівності
11
lo
g
lo
g
.
aa
x
xxx
b) використання означення логарифма: якщо
lo
g
;
b
a
x
bxa
с) використання основної логарифмічної тотожності:
log
;
a
x
ax
d) введення нового невідомого;
e) перехід до нової основи логарифма за формулою
log
log
log
b
a
b
N
N
a
.
220
222
1202.
777
xx
xx
Тому розв’язком рівняння d) буде 2.

43
Частина 2. Початок алгебри
При розв’язанні логарифмічних рівнянь доцільно застосовувати
такий порядок дій:
1) знайти область припустимих значень. При цьому використо
вують те, що log
a
N існує лише при N > 0, а також співвідношення
0, 1, 1;
log 0, 1;
0, 1, 1;
a
якщо N a
NякщоN
якщо a N
2) розв’язують логарифмічне рівняння. При цьому бажано одер
жати
lo
g
,
a
x
b
тоді
,
b
x
a
або
1
lo
g
lo
g
,
aa
x
x
тоді
1
.
x
x
3) перевірити: чи входять знайдені значення невідомої в область
припустимих значень;
4) записати відповідь.
Приклад 9. Розв’язати рівняння:
12
1.
5lg 1lgxx
Розв’язання. У даному випадку областю припустимих значень
буде:
51
0, lg 5, lg 1 0, 10 , 10 .xxx xxx
Введемо нову невідому y = lgx. Тоді задане рівняння набуває
вигляду
2
12
12
11 102 5 1
51
560 2, 3.
yyyy
yy
yy y y
Тепер повернемось до початкової змінної:
з рівності lgx = 2
х
1
= 10
2
= 100;
з рівності lgx = 3
х
2
= 1000.
Розв’язки 100 та 1000 належать області припустимих значень.
44
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Вправи до розділу 2.3
1. Розв’язати лінійні рівняння:
а) 1 + х = 3 – х;b) 2х – 5 = –15 – 3х;
с) 4(х – 3) = 8 – х;d) 3z – 2 + 4(1 – z) = 5(1 – 2z) – 12;
e) 1 – 2[4 – 3(x + l)] = 4(x – 5) – 1.
2. Розв’язати рівняння:
а) (х – 4)
2
= (х – 2)
2
;b) х
2
+ (х + 1)
2
= (2х – 1)(х + 3);
с) (2х + 1)(х – 1) + х
2
= 3(х – 1)(х + 2) – 3;
d) х(х + 2)(х + 4) + х
3
= 2(х + 1)
3
;e) х
4
– 5х
2
+ 6 = 0.
3. Розв’язати рівняння:
a)
22
12
2;
12
xx
x
x
b)
,;
xa xa xb xb
ab ab
xa xb
c)
33
112;xx
d)
2
3
3
440.xx x
4. Розв’язати показникові та логарифмічні рівняння:
a)
2
343 73
76
;
67
xx x
b)
112
66 22 2;
xx xx x
c)
321 1
22277;
xxxxx
d)
21
7187;
x
x
e)
lg5 lg 10 1 lg 2 1 lg 21 20 ;xxx
f)
555
lo
g
9lo
g
10 lo
g
210;xx
g)
lg 1,5 lg ;xx
h)
ln 2 1 3.x
Приклад 10. Обчислити 4
R
, де R = 1+2log
2
9.
Розв’язання.
2
4
2
22
21 log 9
1 2log 9 log 924
44 2 22 4926244.
R

45
Частина 2. Початок алгебри
2.4. Нерівності
Існує багато різновидів нерівностей: лінійні, квадратні, раціо!
нальні, ірраціональні, показникові, логарифмічні, показниково!лога!
рифмічні, з модулями.
Економістам найчастіше треба розв’язувати лінійні (у тому числі
з багатьма невідомими), квадратні, раціональні та показникові не!
рівності.
При розв’язуванні нерівностей використовують такі властивості
нерівностей:
1. Якщо а > b i c є будь&яке дійсне число, тоді а + с > b + с та
а – с > b – с, тобто нерівність не зміниться при додаванні та
відніманні однакового дійсного числа с у обох його частинах.
2. Якщо а > b і с будь&яке додатне число, тоді ас > bc, a
,
ab
cc
тобто нерівність не змінюється, якщо обидві мого частини помножи&
ти або поділити на однакове додатне число с.
3. Якщо а > b і с будь&яке від’ємне число, тоді ас < bc та
,
ab
cc
тобто при множенні та діленні нерівності на від’ємне число нерівність
змінює свій знак на протилежний.
Приклад 11. Розв’язати нерівність
35 2
1.
43
y
y
Розв’язання. Помножимо задану нерівність на 12. Згідно з вла!
стивістю 2 нерівність не зміниться, тобто одержимо
352
12 12 1 12 9 4 5 2 12
43
y
yyy
12 9 20 8 12 12 9 20 4
yy yy
.
Перенесемо члени з невідомим у в ліву частину, а постійні числа
у праву частину нерівності, тоді одержимо
12 20 4 9 8 5
yy y
.

46
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Останню нерівність поділимо на (–8). Тоді, згідно з властивістю
3, нерівність змінює свій знак на протилежний. Отже, маємо:
5
85 ,
8
yy
тобто розв’язком заданого рівняння будуть усі дійсні числа у
5
,.
8
y
Приклад 12. Підприємство виробляє спецодяг, який продає по
60 гривень за кожну одиницю. Матеріал та оплата праці за вироб!
ництво кожної одиниці коштує 40 гривень. Власнику підприємства
треба кожного тижня сплачувати 3000 гривень за оренду приміщен!
ня, охорону, транспортні витрати, оплату праці прибиральниці, бух!
галтера та інше. Скільки одиниць спецодягу повинно виробляти
підприємство кожного тижня, щоб одержувати прибуток не менше
600 гривень щотижня?
Розв’язання. Шукану кількість одиниць спецодягу позначи!
мо х. Згідно з умовою задачі витрати кожного тижня складають
(40х + 3000) гривень, а доход 60х гривень.
Прибуток = доход – витрати = 60х – (40х + 3000) = 20х – 3000.
За умовою задачі треба одержати прибуток не менше 600 гри!
вень, тобто
20 3000 600 20 3600 1800xxx
(одиниць спецодягу).
Приклад 13. Знайти найменший цілий розв’язок нерівності
4
х
– 4
х–3
– 4032 > 0.
Розв’язання. Задану нерівність можна записати у вигляді
33 3 3
4032
4 4 1 4032 4 63 4032 4 64.
63
xxx
тобто
33
44 33 6.
x
xx
Найменшим цілим розв’язком заданої нерівності буде число 7.

47
Частина 2. Початок алгебри
У загальному випадку розв’язування нерівностей вигляду
0, 0, 0, 0fx fx fx fx
для будь!якого виразу доцільно проводити методом інтервалів. Суть
цього методу полягає у тому, що корені рівняння f(х) = 0 розподіля!
ють усю область визначення функції f(х) на інтервали, на яких f(х)
має постійний знак. Тому можна визначити знак функції на кожному
інтервалі шляхом підстановки у функцію замість х будь!якої точки х
0
з інтервалу, що розглядається, а потім обирати такі інтервали, на яких
функція має знак заданої нерівності.
Приклад 14. Розв’язати нерівність
13
23xx
та знайти
найменше ціле додатне значення розв’язку.
Розв’язання. Задана нерівність не існує при х = –2 та х = 3.
Тому областю її визначення буде
,2 2,3 3, .
Запише!
мо задану нерівність так, щоб у правій частині залишився лише 0,
тобто у вигляді
13 336 29
000
23 23 23
xx x
x x xx xx
.
При множенні нерівності на (–1) вона змінює свій знак на про!
тилежний. Тому одержуємо нерівність
29
0
23
x
xx
еквівалентну заданій.
Остання нерівність еквівалентна нерівності
29 2 30, 2, 3fx x x x x x
.
Останню нерівність будемо розв’язувати методом інтервалів.
З рівності (2х + 9)(х + 2)(х – 3) = 0 одержимо
1
9
,
2
x
2
2,x
3
3,x
які поділяють область визначення f(х) на інтервали:
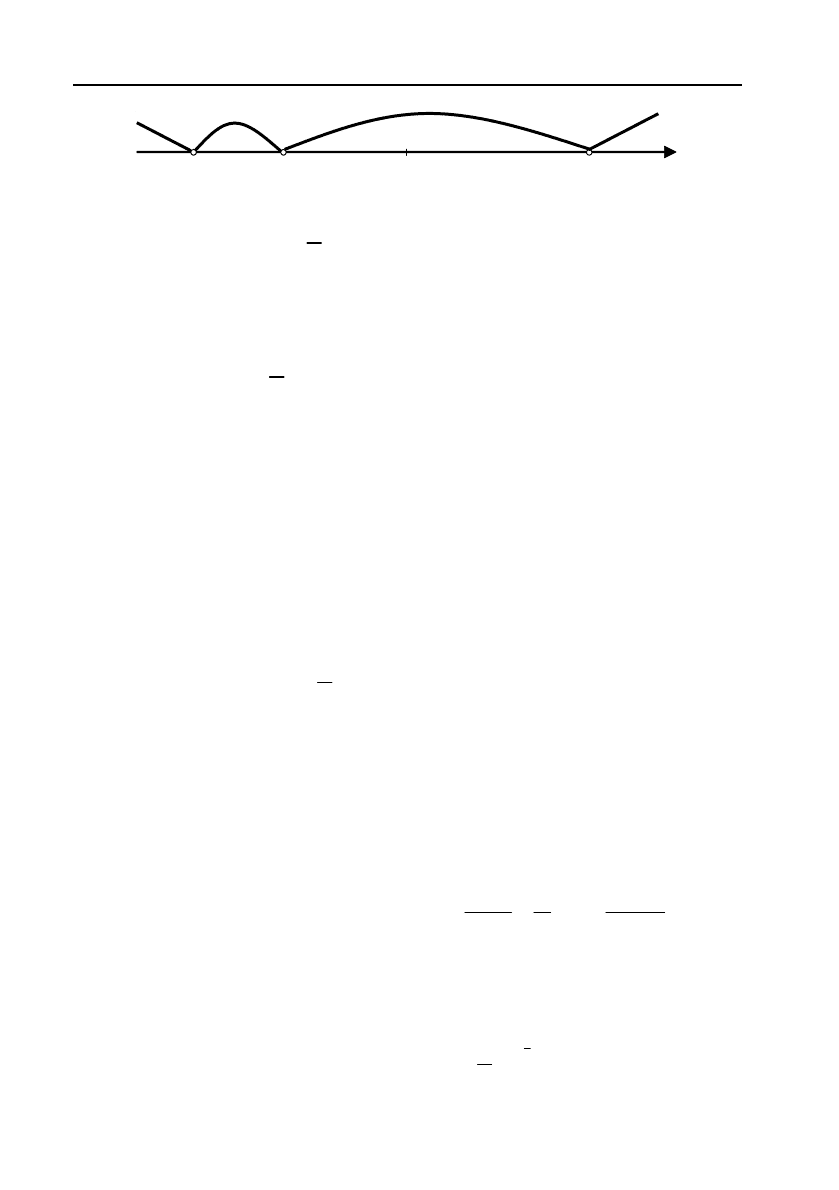
48
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
На інтервалі
9
,
2
візьмемо х
0
= –5, тоді
52595253 1380.f
На інтервалі
9
,2
2
візьмемо х
0
= –3, тоді
36932330.f
На інтервалі (–2, 3) візьмемо х
0
= 0, тоді
09230.f
На інтервалі
3,
візьмемо х
0
= 4, тоді
f(4) = (8 + 9)(4 + 2)(4 – 3) > 0.
Отже, розв’язком заданої нерівності буде об’єднання інтервалів,
де f(х) > 0 тобто
9
,2 3, .
2
x
Найменшим цілим додатним значенням буде 4, оскільки 3 не
належить області визначення.
Вправи до розділу 2.4
1. Розв’язати нерівності:
а) 3(2х – 1) > 4 + 5(х – 1); b)
121
1;
43 6
yy y
с) 1,2(2t – 3)
2,3(t – 1); d) (x – 2)(x – 5) < 0;
e) х
2
– 6х – 9
0; f) х
2
+ 13 < 6х;
g)
25 6 5 5;
xx
h)
2
1
4
log 5 8
2
2,5.
5
xx
х
–9/2 –2
3
0
–
–
+
+

49
Частина 2. Початок алгебри
2. Розв’язати задачі:
a) чоловік має 7000 гривень і бажає вкласти їх, частину під 8%, а
останні під 10%. Яку максимальну кількість коштів він повинен вкла!
сти під 8%, якщо бажає отримати загальний прибуток за рік 600 гри!
вень?
b) кожного місяця фірма може продати х одиниць виробів вартістю
р = 600 – 5х гривень за кожне. Яку кількість виробів треба продати
кожного місяця, щоб одержати не менше 18000 гривень?
c) на вступному іспиті з математики до економічного університе!
ту 15% абітурієнтів не розв’язали жодної задачі, 144 розв’язали за!
дачі з похибками, а кількість абітурієнтів, що розв’язали вірно усі
задачі, відноситься до кількості тих, що не розв’язали жодної задачі
не більше ніж
53
. Скільки абітурієнтів здавали іспит з математики
в той день? Яка кількість їх найбільша?
2.5. Елементи комбінаторики
Фахівцям різних спеціальностей доводиться розв’язувати задачі,
в яких розглядаються ті чи інші комбінації, складені з людей, літер,
цифр чи інших об’єктів.
Так, начальнику цеху потрібно розподілити різні види робіт між
верстатами, що є у наявності, завідуючому навчальною частиною
університету треба складати розклад занять і т.п.
Галузь математики, в якій вивчаються питання про кількість
різних комбінацій, що підпорядковані певним умовам, називають
комбінаторикою. Основні поняття та формули комбінаторики ви!
користовуються при розв’язуванні багатьох проблем життя, менедж!
менту, планування, задач теорії ймовірностей.
Більшість комбінаторних задач розв’язуються з використанням
двох основних правил – правила суми та правила добутку.
Правило суми: якщо деякий об’єкт А можна обрати m спосо!
бами, а об’єкт В – n способами (незалежно від вибору А), тоді вибір
або А або В можна зробити m + n способами.
Наприклад, якщо з двох цехів, в яких працюють 40 та 45 праців!
ників, треба обрати одного на профспілкову конференцію, тоді це
можна зробити 85 способами (обрати з одного цеху – 40 способів, з
другого – 45 способів).

50
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Правило добутку: якщо об’єкт А можна обрати m способами і
після такого вибору об’єкт В обрати n способами, тоді обрання пари
(А, В) у заданому порядку можна зробити mn способами.
Наприклад, якщо з двох класів, в яких навчаються 29 та 31 учнів,
треба направити на міську математичну олімпіаду будь!яких два
учня, по одному з кожного класу, тоді можливих комбінацій буде
29
31 = 899.
Деякі комбінації зустрічаються частіше за інші і мають свої назви:
розміщення, перестановки та сполучення.
В комбінаториці доведені формули, які дозволяють знаходити
кількість цих основних комбінацій. Ці формули разом з правилами
комбінаторики дозволяють знаходити кількість будь!яких комбінацій.
Ознайомимось з основними комбінаціями комбінаторики.
Означення. Комбінації, які взяті з n різних елементів в кількості
k (k < n) елементів і які відрізняються між собою хоча б одним еле&
ментом або розташовані у різному порядку називають розміщення
ми без повторень, їх кількість позначають
k
n
A
або A
n
(k) і знахо&
дять за формулою
!
,
!
k
n
n
A
nk
(1)
де
!123 .nn
Наприклад, якщо у навчальному плані 10 дисциплін і на кожен
день можна планувати 4 різних дисципліни, то розклад занять на
кожний день можна скласти
4
10
10! 12345678910
7 8 9 10 5040
6! 1 2 3 4 5 6
A
способами.
Означення. Різноманітні комбінації з n елементів в кількості k
елементів (k < n), що відрізняються між собою хоча б одним елемен&
том без врахування їх порядку, називають сполученням з n еле
ментів k, їх кількість позначають
k
n
C
або
()
n
Ck
і знаходять за
формулою
