Бардушкин В.В., Кожухов И.Б., Прокофьев А.А., Фадеичева Т.П. Основы теории делимости чисел. Решение уравнений в целых числах
Подождите немного. Документ загружается.

сомножители. Но тогда и в левой части должны сократиться все
сомножители, так как равенство
1
1
=
⋅
⋅
+ ks
рр … невозможно,
поскольку все числа
больше единицы. Следовательно,
разложения числа
п на простые сомножители совпадают
ks
рр ,,
1
…
+
Пусть
N, , и ∈n 1>n
r
pppп
⋅
⋅⋅= …
21
есть разложение п на
простые сомножители. Среди чисел
могут быть и
одинаковые. Пусть
– различные из этих чисел, а
– кратности, с которыми они входят в разложение.
Тогда
r
ppp ,,,
21
…
k
ppp ,,,
21
…
k
ααα ,,,
21
…
k
k
pppn
α
αα
⋅⋅⋅= …
21
21
.
Последнее представление называется каноническим разложением
натурального числа
п, , на простые сомножители. 1>n
Пример.
.
234
11532261360 ⋅⋅⋅=
С помощью канонического разложения
можно представить все делители
п. Они имеют вид:
k
k
pppn
α
αα
⋅⋅⋅= …
21
21
k
k
pppd
β
ββ
⋅⋅⋅= …
21
21
, где
ii
α
≤β≤0 , при ki ,,2,1 …
=
.
Действительно, если
, то по лемме 1 (см. § 1) каждый простой
делитель числа d делит п. Поэтому он содержится среди чисел
и входит в каноническое разложение числа d со
степенью, не большей, чем в каноническом разложении числа
п.
Поэтому
d представляется в виде . Очевидно и
обратное, что каждое число вида
, где
, при , есть делитель п.
nd |
k
ppp ,,,
21
…
k
k
pppd
β
ββ
⋅⋅⋅= …
21
21
k
k
pppd
β
ββ
⋅⋅⋅= …
21
21
ii
α≤β≤0 ki ,,2,1 …=
21
Замечание. Вопросы делимости, связанные с представлением
натуральных чисел в каноническом виде, подробно рассмотрены в § 6
данного пособия.
Теорема 3 (Евклид (
ΙΙΙ
в. до н.э.)). Множество простых чисел
бесконечно.
Доказательство. Допустим противное, что простые числа
образуют конечное множество и – наибольшее
простое число. Рассмотрим число
k
pрр ,,,
21
…
k
p
1
21
+
⋅
⋅
⋅
=
k
pppN … . Оно не
делится ни на одно из простых чисел
, так как при
делении
N на любое из этих чисел остаток равен 1. Но и по
следствию из леммы 5
N должно иметь простой делитель. Полученное
противоречие показывает, что сделанное предположение неверно и
теорема справедлива
k
pрр ,,,
21
…
1>N
Опишем удобный способ выделения простых чисел в данном
отрезке натурального ряда, известный еще греческому ученому
Эратосфену (276–194 г.г. до н.э.). Он состоит в отсеивании составных
чисел, находящихся в данном отрезке, и носит название
«решета
Эратосфена».
Напишем одно за другим числа
. Число 2,
являющееся простым, оставляем и зачеркиваем после него все четные
числа. Первое следующее за
2 незачеркнутое число есть 3. Оно не
делится на
2. Значит, оно не имеет делителей, отличных от 1 и 3, и
поэтому является простым. Оставляем
3 и зачеркиваем после него все
числа, кратные
3. Продолжая этот процесс, найдем все простые числа,
не превосходящие некоторого простого числа
. При этом будут
зачеркнуты все составные числа, кратные
. Первое
незачеркнутое после
число будет простым числом , так как
оно не делится на
и поэтому имеет своими делителями
только
1 и . Если найдено
N,,4,3,2 …
k
р
k
р,,3,2 …
k
р
1+k
р
k
р,,3,2 …
1+k
р Nр
k
≥ , то все оставшиеся
незачеркнутыми числа будут простыми, поскольку все кратные чисел
22
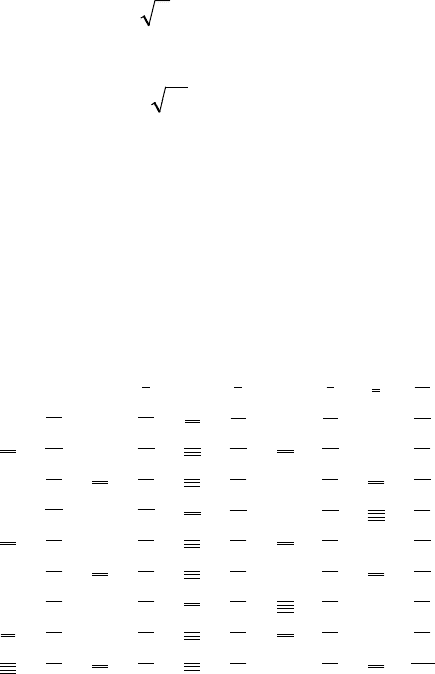
k
р,,3,2 … уже вычеркнуты, а по лемме 6 любое составное число п
имеет простой делитель
п≤ .
Составление таблицы простых чисел, не превосходящих
N,
указанным процессом закончено, как только зачеркнуты все числа,
кратные простым числам
N≤ .
Пример. Составьте таблицу простых чисел в отрезке натурального ряда
от
1 до 100.
Решение. В приводимой ниже таблице подчеркнуты все числа, которые
должны быть вычеркнуты в процессе применения решета Эратосфена
(одной чертой выделены все числа, кратные 2; двумя – все числа,
кратные
3 и не выделенные ранее; тремя – все числа, кратные 5 и не
выделенные ранее при двух предыдущих переборах; четырьмя – все
оставшиеся невыделенными числа, кратные
7):
.100,99,98,97,96,95,94,93,92,91
,90,89,88,87,86,85,84,83,82,81
,80,79,78,77,76,75,74,73,72,71
,70,69,68,67,66,65,64,63,62,61
,60,59,58,57,56,55,54,53,52,51
,
50,49,48,47,46,45,44,43,42,41
,40,39,38,37,36,35,34,33,32,31
,30,29,28,27,26,25,24,23,22,21
,20,19,18,17,16,15,14,13,12,11
,10,9,8,7,6,5,4,3,2
Так как
, то все невычеркнутые числа 2, 3,
5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97
являются простыми.
100121,12111
2
>=
23
Упражнения
2.1. Определите, является ли простым число:
1)*
353; 2)* 767; 3)* 1999; 4) 2003.
Ответ: 1)
353 – простое число; 2) 767 – составное число;
3)
1999 – простое число; 4) 2003 – простое число.
2.2.* Какие из чисел, заключенные между числами
а и b )( ba
<
, яв-
ляются простыми:
1)
, ; 2) , 2320=а 2350=b 40322=a 40330
=
b ;
3)
, ? 3628802=a 3628810=b
Ответ: 1)
2333, 2339, 2341, 2347;
2) среди этих чисел нет ни одного простого;
3) среди этих чисел нет ни одного простого.
2.3.* Докажите, что наименьшее число, взаимно простое с числами
, просто. п,...,3,2
2.4.* Докажите, что для любого натурального
п найдется такое нату-
ральное
х, что число составное. 1+хп
2.5. Докажите, что если число, являющееся квадратом некоторого цело-
го числа, делится на простое число
р, то оно должно делиться и на чис-
ло
.
2
p
2.6. При каких целых
п число является простым? 107
2
+− nn
Ответ: таких п не существует.
2.7. При каких целых
п число является простым? 1
24
++ nn
Ответ:
1
±
.
2.8. Про три простых числа известно, что одно из них является разно-
стью кубов двух других. Какие это числа
?
Ответ:
2, 3, 19.
2.9.* Докажите, что если
– простое число, то 1−
n
a 2
=
a и п – про-
стое число.
2.10.* Докажите, что если число
– простое, то для неко-
торого целого
.
12 +
m n
m 2=
0≥n
24
2.11.* Найдите все простые числа
р такие, что числа 2
+
p и 4
+
p
также простые.
Ответ:
3.
2.12.* Какие остатки при делении на
6 может иметь простое число,
бóльшее
3?
Ответ:
1 и 5.
2.13. Докажите, что если
р и – простые числа , то число
составное.
12 +p 5≥
14 +p
2.14.* Известно, что числа
p, p + 10, p + 14 – простые. Чему равно
число
p?
Ответ:
3.
2.15.* Известно, что числа
p и – простые. Чему равно p? 18
2
+р
Ответ:
3.
2.16.* Известно, что числа
p, 2p + 1, 4p + 1 – простые. Чему равно
число
p?
Ответ:
3.
2.17. Найдите все такие простые числа
р, что число также про-
стое.
12
2
+p
Ответ:
3.
2.18. Докажите, что число
составное для любого натураль-
ного
.
3
3
+− nn
1>n
2.19.* Найдите все такие простые числа
р, что числа и
также простые.
14
2
+p
16
2
+p
Ответ: 5.
2.20. Докажите, что остаток от деления простого числа на
30 либо явля-
ется простым числом, либо равен
1.
2.21.* Докажите, что если
)!1(
−
n не делится на п, то либо 4
=
n , либо
п – простое число.
2.22.* Пусть
. Докажите, что произведение всех простых чисел,
не превосходящих
п, больше п.
2>n
25
2.23.* Докажите, что если
, то между числами п и есть простое
число.
2>n !n
2.24.* Докажите, что если число
п – составное, то число 12
−
п
тоже
составное.
2.25.* Докажите, что квадрат простого числа, бóльшего трех, дает оста-
ток
1 при делении на 12.
2.26.* Докажите, что для любого числа
N в натуральном ряду чисел
можно найти
k идущих подряд составных чисел.
∈k
2.27.* Докажите, что если произведение
ab делится на простое число р,
то хотя бы одно из чисел
а, b делится на р.
2.28.* Докажите, что если сумма и произведение двух целых чисел де-
лятся на простое число
р, то каждое из них делится на р. Верно ли это,
если
р – составное?
2.29.* Найдите простое число
р, если известно, что число 113
+
р яв-
ляется кубом некоторого натурального числа.
Ответ:
2 или 211.
2.30.* Докажите, что при
сумма п последовательных нечетных
чисел, т.е. сумма
2≥п
)122(...)52()32()12(
−
+
+
++
+
+++ nkkkk ,
является составным числом.
2.31.* Докажите, что если
р – простое число, то число при
делится на р. Верно ли это утверждение, если число р не
является простым
?
i
р
С
11 −≤≤ pi
2.32.* Докажите, что число
делится на любое простое число р та-
кое, что
.
п
п
С
2
npп 2≤<
2.33.* Докажите, что число вида
4
4
+п
∈
п( N, п > 1) всегда состав-
ное.
2.34.* Обозначим через
п-ое по порядку простое число. Докажите,
что
.
n
p
np
n
2≥
26

2.35.* Обозначим через
п-ое по порядку простое число. Докажите,
что
.
n
p
1
2
2
−
≤
n
n
p
2.36.* Пусть
р – простое число. Докажите, что единственным решением
в целых числах уравнения
является
.
0
3233
=++ zppyx
0=== zyx
2.37.* Докажите, что существует бесконечно много простых чисел, даю-
щих при делении на
3 остаток 2.
2.38.* Докажите, что простых чисел вида
14
−
k бесконечно много.
2.39.* Из чисел от
1 до вычеркнуты все числа, делящиеся на 2,
3, 5 и 7. Какая часть первоначально взятых чисел осталась невычеркну-
той
?
!1000
Ответ:
35
8
7
1
1
5
1
1
3
1
1
2
1
1 =
⎟
⎠
⎞
⎜
⎝
⎛
−⋅
⎟
⎠
⎞
⎜
⎝
⎛
−⋅
⎟
⎠
⎞
⎜
⎝
⎛
−⋅
⎟
⎠
⎞
⎜
⎝
⎛
−
.
2.40.* Докажите, что среди чисел от
1 до а (включительно) имеется
⎥
⎦
⎤
⎢
⎣
⎡
b
a
чисел, делящихся на b. (Через
⎥
⎦
⎤
⎢
⎣
⎡
b
a
обозначена целая часть чис-
ла
ba .)
2.41.* Числа b и c взаимно просты. Сколько имеется чисел от 1 до а,
делящихся хотя бы на одно из чисел
b, c?
Ответ:
⎥
⎦
⎤
⎢
⎣
⎡
−
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
cb
а
с
а
b
a
.
2.42. Докажите, что число является составным, разложив
его на два целых сомножителя, бóльших 6000 (не вычисляя самого
числа, а используя только его выражение).
133
1724
++
Ответ:
. )1333233(6535
3681116
+++⋅++⋅
2.43. Найдите все упорядоченные тройки простых чисел
,
удовлетворяющие равенству
.
);;( rqp
rqp
pq
=+
Ответ: , . )17;3;2( )17;2;3(
27
§ 3. Сравнения
В ходе дальнейшего изложения будем считать, что число
т
является натуральным.
Определение. Целые числа
а и b сравнимы по модулю т, если они
имеют одинаковые остатки от деления на
т (при этом используется
запись
). )(modmba ≡
Замечание. Запись
означает делимость а на т. )(mod0 mа ≡
Пример.
. )7(mod410 ≡−
Из определения следует, что все целые числа по модулю
т
разбиваются на
т непересекающихся классов сравнимых между собой
чисел (т.е. чисел, имеющих одинаковые остатки при делении на
т):
110
,,,
−m
KKK …
.
Каждое число, входящее в какой-либо из классов, называется
вычетом этого класса, а сами классы – классами вычетов по модулю
т.
Беря по одному вычету из каждого класса, получим полную систему
вычетов по модулю
т.
Пример. Классами чисел по модулю
4 являются:
}{
...,4,...,8,4,0,4,8,...,4,...
0
nnK −−−= ,
}{
...,14,...,9,5,1,3,7,...,14,...
1
+
−−+−= nnK ,
}{
...,24,...,10,6,2,2,6,...,24,...
2
+
−−+−= nnK ,
}{
...,34,...,11,7,3,1,5,...,34,...
3
+
−−+−= nnK .
Совокупность
образует одну из полных систем
вычетов по модулю 4. Полной системой наименьших неотрицательных
вычетов по модулю
4 является . Полной системой
наименьших по абсолютной величине вычетов по модулю 4 является
, а также
{}
{
23,2,11,8 −
}
}{
3,2,1,0
{}
1,2,1,0 − 1,2,1,0 −
−
.
28
Теорема 4. Пусть Z. Соотношение ∈ba , )(mod mba
≡
имеет
место тогда и только тогда, когда
. )(| bam −
Доказательство.
Ö Если , то )(modmba ≡ rmqa
+
=
1
,
. Следовательно, rmqb +=
2
)(
21
qqmba
−
⋅
=− . Значит,
)(| bam −
Õ Если , то . Если )(| bam − mхba =− rmqb
+
=
, то
. Следовательно, rхqma ++⋅= )( )(mod mba ≡
Замечание. Из теоремы следует, что класс чисел по модулю
т,
содержащий число
Z, состоит из всех чисел ∈a
∈
х
Z вида
mqa
x
+= .
Свойства сравнений.
1. Рефлексивность:
. )(mod mаa ≡
Доказательство. Очевидно; следует из определения.
2. Симметричность: если
)(mod mba
≡
, то )(mod mab
≡
.
Доказательство. Очевидно; следует из определения.
3. Транзитивность: если
и )(mod mba ≡ )(mod mcb
≡
, то
. )(mod mca ≡
Доказательство. Очевидно; следует из определения.
4. Если
, , то )(mod
11
mba ≡ )(mod
22
mba ≡
)(mod
2121
mbbaa +≡+ .
Доказательство. По теореме 4
111
mхba
=
− ,
222
mхba
=
−
.
Следовательно,
)(
212211
xхmbaba
+
⋅
=
−+
−
, или
. Таким образом, согласно
этой же теореме,
)()()(
212121
xхmbbaa +⋅=+−+
)(mod
2121
mbbaa +
≡
+
29
5. Если
, то . )(mod mbсa ≡+ )(mod mсba −≡
Доказательство. По теореме 4
mxbсa
=
−
+
, или
. Таким образом, согласно этой же теореме,
mxcba =−− )(
)(mod mсba −≡
6. Если
, то , где )(mod mba ≡ )(mod mbmka ≡+
∈
k Z.
Доказательство. По теореме 4
mхba
=
− , следовательно,
, или )( kхmmkba +⋅=+− )()( kхmbmka
+
⋅
=
−
+
.
Таким образом, согласно этой же теореме,
)(mod mbmka
≡
+
7. Если
, , то )(mod
11
mba ≡ )(mod
22
mba ≡
)(mod
2121
mbbaa ⋅≡⋅ .
Доказательство. По теореме 4
111
mхba
+
= ,
222
mхba
+
=
.
Следовательно,
)(
2112212121
xmxxbхbmbbaa
+
+
⋅+
=
, или
. Таким образом, согласно этой же теореме,
mkbbaa =−
2121
)(mod
2121
mbbaa ⋅≡⋅
8. Если , то , где )(mod mba ≡ )(mod mba
nn
≡
∈
n N
0
.
Доказательство. Следует из предыдущего свойства.
9. Если
, то . )(mod mba ≡ )(mod mbkak ≡
Доказательство. По теореме 4
mхba
=
−
, значит,
. Таким образом, согласно этой же теореме,
)(хkmbkak ⋅=−
)(mod mbkak ≡
10. Если
, то , где )(mod mba ≡ )(mod mkbkak ≡
∈
k N.
Доказательство. По теореме 4
mхba
=
−
, значит,
. Таким образом, согласно этой же теореме,
xmkbkak ⋅=− )(
)(mod mkbkak ≡
30
