Бабенко Л.К. Организация и технология защиты информации: Введение в специальность
Подождите немного. Документ загружается.

21
X
0
X
1
X
2
X
3
X
4
X
5
X
6
K
7
)T(T
0
i
ш
i
)T(T
ш
i
0
i
СМ
5
ш
i
Г
N
6
N
5
СМ
4
СМ
3
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
32...
...1
N
4
N
3
N
2
N
1
СМ
1
КЗУ
X
7
K
R
СМ
2
K
6
K
5
K
4
K
3
K
2
K
1
K
8
C1 const C2 const
mod 2
32
- 1 mod 2
32
mod 2
32
Цикл. сдвиг на 11 шагов
в сторону старш. разряда
mod 2
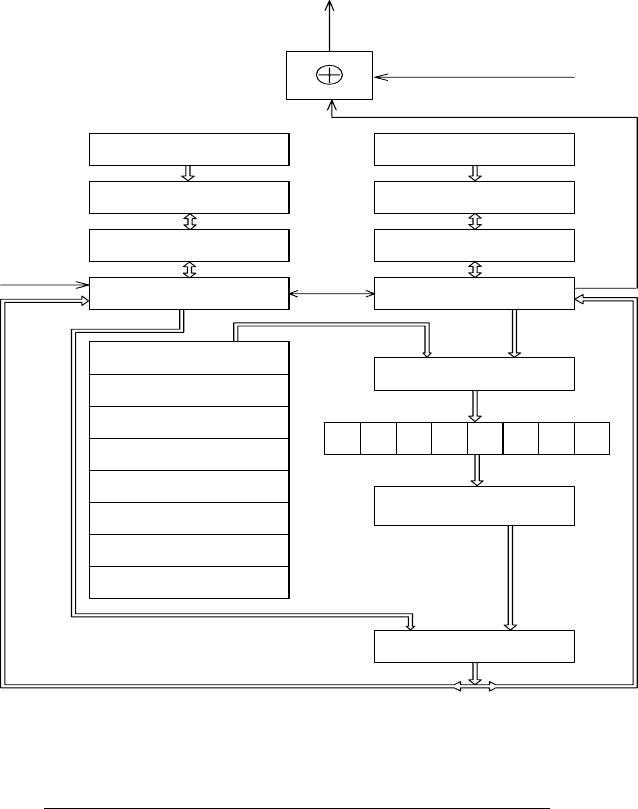
Рис.1.9 Режим гаммирования ГОСТ 28147-89
Открытое распределение ключей. Схема Диффи-Хеллмана
Важной составной частью шифрсистемы является ключевая система
шифра. Под ней понимается описание всех видов ключей (долговременных,
суточных, сеансовых и других) и алгоритмов их использования.

22
Одной из основных характеристик ключа является его размер
, опреде-
ляющий число всевозможных ключевых установок шифра. Если размер ключа
чрезмерно велик, то это приводит к удорожанию изготовления ключей, услож-
нению процедуры установки ключа, понижению надежности работы шифрую-
щего устройства.
Важнейшей частью практической работы с ключами является обеспе-
чение секретности
ключа. К основным мерам по защите ключей относятся сле-
дующие:
- ограничение круга лиц, допущенных к работе с ключами;
- регламентация рассылки, хранения и уничтожения ключей;
- регламентация порядка смены ключей;
- применение технических мер защиты ключевой информации от несан-
кционированного доступа.
Рассмотрим один из принципов распределения ключей (на основе од-
носторонней
функции), проработка которого имела весьма неожиданные
последствия - была изобретена система шифрования с открытым ключом.
Сначала небольшое отступление.
Понятие односторонней функции было введено в теоретическом иссле-
довании о защите входа в вычислительные системы . Функция f(x) называется
односторонней (one-way function), если для всех x из ее области определения
легко вычислить y=f(x), но нахождение по заданному y
0
такого x
0
, для которого
f(x
0
)=y
0
, вычислительно неосуществимо, то есть требуется настолько огромный
объем вычислений, что за них просто и не стоит браться.
Однако существование односторонних функций не доказано. В качест-
ве приближения была предложена Гиллом Дж. целочисленная показательная
функция f(x)=a
x
(mod n), где основание a и показатель степени x принадлежат
интервалу (1,n-1), а умножение ведется по модулю n (3*4 mod 10=2;
7*8mod 9=2). Функция вычисляется достаточно эффективно по схеме Горнера.
Если представление числа x в двоичной форме имеет вид
x
k-1
2
k-1
+ x
k-2
2
k-2
+ ...+ x
1
2
1
+ x
0
2
0
,
то
y = f(x) = a
x
mod n = ((...(a
xk-1
)
2
*a
xk-2
)
2
*...*a
x1
)
2
*a
x0
mod n.
Операция, обратная к этой, известна как операция вычисления дискрет-
ного логарифма: по заданным y, a и n найти такое целое x, что a
х
( mod n) = y.
До настоящего времени не найдено достаточно эффективных алгоритмов реше-
ния этой задачи.
Американские криптологи Диффи и Хеллман (Diffi W., Hellman M.E.
New direction in criptography. IEEE Trans. Inf. Theory, v. IT-22, 1976) предложили
схему распространения (рассылки) ключей для секретной связи на основе одно-
сторонней показательной функции. Ее суть состоит в следующем.
В протоколе обмена секретными ключами предполагается, что все
пользователи знают некоторые числа n
и a (1< a < n). Для выработки общего
23
секретного ключа пользователи A и B должны проделать следующую процеду-
ру:
1. Определить секретные ключи пользователей К
А
и К
В
.
Для этого каждый пользователь независимо выбирает случайные числа
из интервала (1,..., n-1).
2. Вычислить открытые ключи пользователей Y
A
и Y
B
.
Для этого каждый использует одностороннюю показательную функцию
Y=a
k
mod n со своим секретным ключом.
3. Обменяться ключами Y
A
и Y
B
по открытому каналу связи.
4. Независимо определить общий секретный ключ К.
Для этого пользователи выполняют вычисления с помощью той же од-
носторонней функции
A: Y
B
KA
(mod n) =
[
a
KB
]
KA
mod n = a
KA*KB
mod n = K.
B: Y
A
KB
(mod n) =
[
a
KA
]
KB
mod n = a
KB*KA
mod n = K.
Здесь каждый имеет показатель степени, а основание получает от парт-
нера
Безопасность (секретность) изложенной схемы зависит от сложности
вычисления секретных ключей пользователей (К
А
и К
В
). Пока не найдено удов-
летворительных быстрых алгоритмов нахождения К из а, Y
A
и Y
B
без явного
определения К
А
или К
В
.
1.5. Криптосистемы с открытым ключом
Дальнейшим развитием идеи односторонней функции стало введение
односторонней функции с секретом, а затем и системы шифрования с открытым
ключом.
Под односторонней функцией с секретом (с лазейкой, с потайной две-
рью - a trap-door one-way) называется зависящая от параметра k фукция y=f
k
(x),
такая, что знание k дает возможность легко построить обратное преобразование
x=f
-1
(y), тогда как без знания k определение х по известному y вычислительно
не осуществимо.
В принципе, основой таких функций является некоторая базовая функ-
ция, имеющая параметр n, который может принимать множество значений из
широкого диапазона. Известен некоторый способ определения обратной базо-
вой функции, основанный на определенном сочетании свойств параметра n.
Важно, чтобы определение сочетания свойств
параметра n по его значению бы-
ло вычислительно неосуществимо. Тогда, задав сочетание, определяем n, пря-
мую и обратную базовые функции, причем последнюю держим в секрете. Зна-
чит, n выступает как открытый ключ, а обратное преобразование - как секрет-
ный ключ.
24
Один из первых предложенных примеров таких функций основан на
степенной функции f(x)=x
m
(mod n), вычисление которой по известным n и m
производится достаточно эффективно. Преобразование, обратное к возведению
в степень x
m
(mod n) называется вычислением корня m-й степени по модулю n.
Например, 5
4
mod 21 = 16, поэтому 5 является корнем 4-й степени из 16 по мо-
дулю 21; 4
5
mod 25 = 24, 4 - есть корень 5-й степени из 24 по mod 25. В на-
стоящее время эффективный алгоритм этой операции известен, но требует зна-
ния специального разложения n по степеням простых чисел. Эта информация и
является секретным ключом. Определить такое разложение по значению n дос-
таточно сложно, но задав такое разложение мы однозначно определяем n.
Таким образом, криптосистема с
открытым ключом включает откры-
тый алгоритм E
k
шифрования и секретный алгоритм дешифрования D
k
, обрат-
ный к E
k
, но определение которого по E
k
вычислительно не осуществимо.
Иногда принято секретное преобразование D
k
называть секретным клю-
чем (private key), а открытое преобразование E
k
- открытым ключем (public key),
поэтому сами системы называют также двухключевыми
криптосистемами (two
key cryptosystem). Другое название таких криптосистем - асимметричные
крип-
тосистемы (asymmetric cryptosystem), в то время как обычные криптосистемы с
секретным ключом называются симметричными (symmetric criptosystem).
Так как в силу открытости любой злоумышленник имеет доступ к пре-
образованию зашифрования E
k
, то он может всегда выбрать любой открытый
текст и получить соответствующий ему шифртекст. Поэтому криптосистемы с
открытым ключом должны быть устойчивы к методам дешифрования по вы-
бранным открытому и шифрованному тексту.
Криптосистема RSA
Название криптосистемы образовано из первых букв фамилий предло-
живших ее авторов (Rivest R., Shamir A., Adleman L. A method for obtaining
digital signatures and pablic-key cryptosystems. Commun. ACM, v.21, N2, 1978).
Система относится к блочным экспоненциальным системам, так как
каждый блок М открытого текста рассматривается как целое число в интервале
(0,..., n-1) и преобразуется в блок С следующим открытым преобразованием
C = E (e,n) (M) = M
e
(mod n),
где E(e,n) - преобразование, а (e,n) - ключ зашифрования.
При расшифровании блок открытого текста М восстанавливается таким
же преобразованием, но с другим показателем степени.
M = D (d,n) (C) = C
d
(mod n),
где D(d,n) - преобразование, а (d,n) - ключ расшифрования.
В основе этого метода лежит довольно сложное теоретическое обосно-
вание. Числа e и d связаны с n определенной зависимостью и существуют реко-
мендации по выбору ключевых элементов на основе простых чисел. Если взять
два простых числа p и g, определить n = p х q, то можно определить пару чисел

25
e и d, удовлетворяющих заданным условиям. Если сделать открытыми числа e и
n, а ключ d (и обязательно p и g) держать в секрете - то предложенная система
является RSA-криптосистемой открытого шифрования. Очевидно, ее стойкость
определяется сложностью операции извлечения из С корня степени е по моду-
лю n.
Рассмотрим основные этапы реализации алгоритма RSA.
1. Отправитель вычисляет n = p х q и M=(p-1)(q-1).
2.
Затем он выбирает случайное целое число e, взаимно простое с М и
вычисляет d, удовлетворяющее условию
ed = 1 (mod M).
Напомним, что два числа являются взаимно простыми, если их HOD
=1. Числа а и b имеют HOD d, если d делит и а и b и максимальный среди таких
чисел.
3. После этого он публикует е и n как свой открытый ключ шифрова-
ния, сохраняя
d, как закрытый (секретный) ключ.
4. Рассмотрим теперь числа e и d. Предположим, что мы знаем одно из
них и знаем соотношение, которым они связаны. Мы могли бы легко вычислить
второе число, однако мы не знаем чисел p и q. Следовательно можно одно из
чисел подарить кому-нибудь вместе с n и попросить его посылать нам сообще
-
ния следующим образом.
5. Сообщение представить как векторы (блоки) длины l
X= (x
1
,x
2
...,x
l
)
0<x
i
< M;
6. Каждое x
i
возвести в степень e по mod n.
7. Прислать нам Y=(x
1
e
(mod n), x
2
e
(mod n),...,x
l
e
(mod n)).
Обозначим t=y
i
=х
i
e
(mod n) и рассмотрим расшифрование полученной
информации.
Для этого возведем полученное число t в степень второго числа пары -
d:
R=t
d
(mod n) = x
e
(mod n)
d
(mod n) = x
ed
(mod n).
В соответствие с п.2 соотношение ed=1(mod M). а это означает, что ed-
1 делится нацело на (p-1)(q-1), т.е. ed=1+a(p-1)(q-1),
где а - целое число.
Утверждается, что
х
ed
(mod n) =x.
Действительно,
x
ed
(mod n) = x
1+a(p-1)(q-1)
(mod n)
Учитывая,что
x
p-1
= 1 mod p, x
q-1
= 1 mod q (эти соотношения доказываются как малая
теорема Ферма, например в /10/) получим
x
(p-1)(q-1)
= 1(mod pq)
x
1+a(p-1) (g-1)
(mod n) = x, т.к.

26
x
a(p-1) (q-1)
= 1(mod pq), из-за того,
что x
(p-1) (q-1)
= 1(mod pq),
x mod n = x, так как x<M.
Что и требовалось доказать.
Цифровая (электронная) подпись
Одним из основных применений криптосистем с открытым ключом яв-
ляется их использование при создании так называемой цифровой или электрон-
ной подписи (digital signature). Впервые идея цифровой подписи была высказана
в работе Диффи и Хеллмана.
Один из вариантов изложения принципа электронной подписи выгля-
дит так. Требуется, чтобы существовали взаимообратные преобразования E
k
и
D
k
, для которых выполняется
E
k
[D
k
(M)] =M для любого открытого текста М.
Тогда D
k
считается секретным преобразованием, с помощью которого
пользователь может зашифровать исходный текст C=D
k
(M) и послать это зна-
чение в качестве цифровой подписи к сообщению М другим пользователям,
обладающим знанием открытого преобразования E
k
. Очевидно, что
определение D
k
при знании E
k
должно быть вычислительно неразрешимой
задачей. Система RSA широко используется в системе цифровой подписи, так
как ее преобразования обладают всеми необходимыми свойствами. Использо-
вание цифровой подписи предполагает существование двух процедур:
подписывания и проверки /8.9/.
Процедура подписывания
сообщения M – это возведение числа M в сте-
пень d по mod n:
S = M
d
(mod n).
Число S есть цифровая подпись, которую может выработать только
владелец секретного ключа.
Процедура проверки
подписи S , соответствующей сообщению M – это
возведение числа S в целую степень e по mod n:
M’= S
e
(mod n).
Если M’= M, то сообщение M признается подписанным пользователем,
который предоставил ранее открытый ключ e.
В реализации для сокращения времени подписывания и размера подпи-
си, в качестве источника для подписи служит не само исходное сообщение М
(произвольной длины), а некоторая производная от него (фиксированной дли-
ны). Для ее получения используется общеизвестная функция Н, отображающая
любое сообщение М в сообщение Н(М) фиксированного малого размера, кото-
рое далее преобразуется в цифровую подпись. Функция Н называется функцией
хеширования (hash function), в простейшем случае это может быть, например,
функция вычисления контрольной суммы текста сообщения по модулю 2
32
, раз-

27
мер приведенного для электронного подписывания сообщения тогда будет ра-
вен 32 двоичным разрядам (четырем байтам).
2. Программно-аппаратные средства защиты информации в компьютерах
2.1. Программные средства защиты от копирования
и несанкционированного использования
Методы защиты данных в компьютере можно разделить на механиче-
ские, аппаратные и программные.
К механическим способам относятся разнообразные крышки
и чехлы с
замками, клейкие пластины для приклеивания терминала к компьютеру, а ком-
пьютера к столу, запираемые помещения с сигнализацией и другие.
Аппаратные средства реализуются в виде специальных электронных
модулей, подключаемых к системному каналу компьютера или портам ввода-
вывода, и осуществляющих обмен кодовыми последовательностями с защи-
щенными программами.
Наиболее разнообразны
программные средства. Сюда относятся про-
граммы шифрации данных по задаваемому пользователем ключу, администра-
торы дисков, позволяющие ограничить доступ пользователей к отдельным ло-
гическим дискам, методы установки программного продукта с дистрибутивных
дискет, позволяющие выполнить установку не более заданного числа раз, за-
пуск защищаемых программ посредством не копируемых ключевых дискет,
специальные защитные программные
оболочки, куда погружаются защищаемые
программы и многие другие.
Рассмотрим некоторые программные средства защиты программного
обеспечения от копирования.
Задача защиты программного обеспечения – создание и идентификация
некоторого уникального ключевого признака. В процессе запуска или при рабо-
те защищенное приложение проверяет этот уникальный ключевой признак. Ес-
ли обнаруживается, что ключевой признак совпадает с
эталоном, хранящимся в
защищенной программе, то программа продолжает выполнение, если нет, про-
грамма прекращает свою работу.
Привязка к местоположению на диске
Если требуется исключить копирование программы с жесткого диска на
другой жесткий диск, её можно привязать к номеру кластера или сектора, с ко-
торого начинается файл программы на диске. Привязка осуществляется сле-
дующим образом. Специально подготовленная установочная программа откры-
вает файл с рабочей программой и по таблице открытых файлов находит на
-

28
чальный номер кластера. Это число, являющееся своеобразным ключом, запи-
сывается установочной программой в определенное место файла рабочей про-
граммы (естественно в поле данных). Рабочая же программа после запуска,
прежде всего, выполняет ту же операцию: определяет начальный адрес, а затем
сравнивает его с ключом. Если числа совпадают, программа приступает к вы-
полнению своей содержательной части, если не совпадают – аварийно заверша-
ется. При копировании программы на другой диск (или даже на тот же самый)
она окажется расположенной в другом месте, и номер кластера, записанный
установочной программой, уже не будет соответствовать реальному адресу
файла, в то же время с помощью установочной дискеты программу не
трудно
установить на любом диске.
Запись ключа за логическими пределами файла
Как известно, DOS выделяет место под файлы целыми кластерами, в ре-
зультате чего за логическим концом файла практически всегда имеется свобод-
ное пространство (до конца кластера). При копировании файла на другой диск
реально переносятся только байты, соответствующие самому файлу, так как
число копируемых байтов определяется логической длиной файла. Байты по-
следнего
кластера файла, находящиеся за логическими пределами файла, не
копируются. Если в них записать ключ, то при копировании ключ исчезнет.
Методика работы с программой не отличается от уже описанной. После записи
рабочей программы на жесткий диск, она устанавливается с помощью специ-
альной установочной программы (хранящейся на дискете). Установочная про-
грамма открывает
файл с рабочей программой, перемещает указатель файла на
его конец и записывает ключ (одно или несколько слов) за прежними предела-
ми файла. Затем с помощью средств DOS файл укорачивается до прежней дли-
ны. В результате ключ оказывается физически прилегающим к файлу, но логи-
чески за его пределами. При использовании этого метода установочная
про-
грамма должна перед записью ключа проанализировать длину файла. Если файл
занимает целое число кластеров, его предварительно следует удлинить так, что-
бы он занял часть следующего кластера, иначе некуда будет записать ключ. То
же получится, если, скажем, при длине ключа 2 байта файл занимает целое чис-
ло кластеров минус 1 байт. В
этом случае файл также требует удлинения.
Рабочая программа после запуска выполняет те же операции, что и ус-
тановочная (за исключением удлинения файла) и проверяет, записан ли извест-
ный ей ключ за концом файла.
Ключевая дискета с нестандартным форматом
Достаточно надежный способ защиты программ от переноса на другие
компьютеры заключается в использовании не копируемой ключевой дискеты. В

29
этом случае рабочая программа, находящаяся на жестком диске, перед началом
работы проверяет наличие на дисководе дискеты с ключевой информацией. Для
того, чтобы ключевую дискету нельзя было размножить с помощью команды
DISKCOPY, осуществляющей копирование на физическом уровне, ключевая
информация записывается на дорожке с нестандартным форматом, располо-
женной к тому же за пределами
рабочего пространства диска.
Такая ключевая дискета подготавливается специальной установочной
программой, которая с помощью функции 05h прерывания BIOS 13h, форма-
тирует, например, дорожку номер 40 (или 80) с размером сектора 256 байт вме-
сто 512 и записывает на неё заданный ключ.
Рабочая программа перед началом осуществляет чтение нестандартной
дорожки и при отсутствии самой дорожки или ключа на ней
аварийно заверша-
ется.
Привязка к параметрам среды
Можно осуществлять защиту файла (т. е. выявлять факт незаконного
копирования файла на другой компьютер) используя так называемую "привязку
к параметрам среды" (т.е. к определенным характеристикам аппаратной и
программной части ЭВМ). Для реализации этого метода обычно используют
так называемый "пристыковочный модуль" (ПМ).
Модуль – это часть кода, которая получает управление либо
перед нача-
лом выполнения основной программы, либо после её завершения (хотя, в
принципе, возможны ситуации, когда этот модуль получает управление не
один раз за время отработки программы).
Требования к ПМ:
-подключение к файлу любого размера;
-исходный текст (код) защищаемого файла после подключения ПМ
трудно отделить от защиты;
-ПМ не
должен накладывать ограничений на защищаемый файл.
Характеристики, проверяемые ПМ:
-динамические;
-статические.
Динамические характеристики
– это, например, скорость вращения
жесткого диска (HDD), точная частота работы микропроцессора (CPU).
Недостаток динамических характеристик:
сильная зависимость этих
характеристик от температуры, влажности, напряжения, частоты сети, износа
отдельных частей ЭВМ.
Статические характеристики
– это, например:
- тип микропроцессора в совокупности с разрядностью шины дан-
ных;
- тип сопроцессора для работы с плавающей точкой;

30
- тактовая частота работы микропроцессора (с точностью до единиц
мегагерц);
- тип ПЭВМ;
- дата регистрации BIOS;
- сигнатура производителя BIOS и её адрес в оперативной памяти,
контрольная сумма байтов BIOS;
- размер основной оперативной памяти;
- размер расширенной памяти;
- размер дополнительной отображаемой памяти;
- тип клавиатуры;
- тип видеоадаптера;
- тип
и интерфейс "мыши";
- число параллельных (LPT) портов;
- число последовательных (RS232) портов;
- тип и число НЖМД;
- тип и число НГМД.
2.2.Защита программного обеспечения от копирования с помощью
электронных ключей
Использование электронных ключей относится к аппаратным средствам
защиты.
Ключ представляет собой устройство, имеющее два разъема: одним он
подсоединяется к
параллельному или последовательному порту компьютера,
другой служит для подключения принтера, модема или прочих устройств. При
этом ключ не влияет на работу порта, полностью «прозрачен» для подключае-
мых через него устройств и не мешает их нормальной работе.
Интеллектуальные и физические возможности ключа во многом опре-
деляются той базой, на которой собран ключ
. Современные ключи собирают на
базе микросхем энергонезависимой электрически перепрограммируемой памя-
ти, так называемой EEPROM-памяти (Electrically Erasable Programmable Read
Only Memory); на базе заказных ASIC – чипов (Application Spesific Integrated
Circuit) с памятью или без; на базе микропроцессоров.
Ключи на базе EEPROM
Это самые простые и недорогие ключи, выпускаемые для параллельно-
го порта CENTRONICS. Для обеспечения каскадирования дополнительно ис-
пользуется мультиплексор. Количество ключей, которые могут работать кас-
кадно, обычно не превышает трех. Из-за типовых схемотехнических решений
эти ключи имеют «прозрачность» только для принтеров, работающих в стан-
дартном протоколе CENTRONICS. Двунаправленный протокол, в котором
ра-
