Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics

Подождите немного. Документ загружается.

24 3 Basics of polynomial theory

linear polynomial cx + d = 0 which is solved for x by simply multiplying both

sides of the equation by the inverse of c, provided that c 6= 0 holds. The solution

thus becomes x = −c

−1

d. Linear polynomials, i.e., polynomials of degree 1 ﬁnd

use in manipulating levelling and gravimetric observations. In these cases, they

are manipulated in vector space through the solution of linear algebraic equation

Ax + y = 0 to give the solution x = (A

−1

y, provided that A

A is regular.

Polynomials of degree 2 are known as quadratic polynomials. For univariate

cases, they take the form ax

+ bx + c = 0. For simple cases such as x

+ 2x = 0,

the solution can be obtained by factorization, e.g., x(x + 2) leading to x = 0 or

x = −2. The general solution of quadratic equations of the form ax

+ bx + c = 0

with real coeﬃcients {a, b, c} is given by the quadratic formulae

x =

−b ±

√

− 4ac

, (3.8)

x =

−b ±

√

− 4ac

. (3.9)

Press [334] discourages the use of (3.8) or (3.9) in the determination of the two

roots for cases where a or c (or both) are small since this leads to inaccurate solu-

tions. The main reason cited is that when either the coeﬃcient a or c (or both) is

small, one of the roots involves the subtraction b from a very nearly equal value.

They instead propose the formular

q = −

[b + sgn(b)

− 4ac] , (3.10)

with Sign(x) giving -1, 0 or 1 depending on whether x is negative, zero, or positive.

The two roots are then given by

, x

. (3.11)

In computer algebra software of Matlab and Mathematica, the roots of a quadratic

polynomial are obtained via

• Matlab: x = roots

([a b c]),

where

[a b c]

is a vector containing the coeﬃcients

in the ﬁeld R of reals. The quadratic equation can also be solved using the solve

command, e.g., solve(‘ax

+ bx + c = 0, x

), where x indicates the variable to

be solved.

• Mathematica: x = Root[f, k], where f is the quadratic equation and k the k

root. The quadratic equation can als o be solved using the solve command, e.g.,

Solve[ax

+ bx + c == 0, x].

In general, every quadratic polynomial has exactly two real or two complex ro ots.

From the coeﬃcients, if b

− 4ac > 0, the roots are real but if b

− 4ac < 0 the

roots are a pair of non real complex numbers. The case where b

− 4ac = 0 gives

real and identical roots and is also known as the bifurcation point upon which the

roots change sign.

3-6 Univariate polynomials with real coeﬃcients 25

3-62 Cubic polynomials

These are polynomials of degree 3 and take the form ax

+ bx

+ cx + d = 0.

Like quadratic polynomials, simple cases can also be solved via factorization

e.g., x

− 2x = 0 is factored as x(x

− 2) to give the solutions x = 0, x = −

√

2 or

x = +

√

2. Another approach would be to reduce the cubic polynomial such that

the p olynomials of degree 2 are eliminated to give a simpliﬁed version of the form

+ ey + f = 0 known as a reduced cubic polynomial. The simpliﬁed version can

then be solved for the roots via Cardano’s formula as

y =

−

√

T +

−

√

T , (3.12)

where T = (

)

. Once one real root say ξ

has b een obtained, the polynomial

+ey +f = 0 is divided by (y −ξ

) and the resulting quadratic polynomial solved

for the remaining roots. An alternative approach is presented by [334] who proceed

as follows: Let {a, b, c} be the real coeﬃcients of a cubic polynomial. Compute







K ≡

− 3b

L ≡

− gab + 27c

(3.13)

If K and L are real, and L < K, then the cubic polynomial has three real roots

computed by







= −2

√

Kcos(

) −

= −2

√

Kcos(

Θ + 2π

) −

= −2

√

Kcos(

Θ − 2π

) −

(3.14)

where

Θ = cos

−1

(

√

Using computer algebra software of Matlab and Mathematica the roots of a cubic

polynomial are obtained via

• Matlab: x = roots

([a b c d]),

where

[a b c d]

is a vector containing the coeﬃ-

cients in the ﬁeld R of reals. The quadratic equation can also be solved using

the solve command, e.g., solve(‘ax

+ bx

+ cx + d = 0, x

The origin of the equation is traced by the authors to chapter VI of Fran¸cois Vi`ete’s

treatise “De emendatione” Published in 1615

26 3 Basics of polynomial theory

• Mathematica: x = Root[f, k], where f is the cubic equation, and k, the k

root. The quadratic equation can als o be solved using the solve command, e.g.,

Solve[‘ax

+ bx

+ cx + d == 0, x

]. Considering a = 1, the solution is

x =











−(b/3) −

(1/3)

(−b

+3c))

(3(−2b

+9bc−27d+3

√

−b

+4c

+4b

d−18bcd+27d

)

(1/3)

)

(−2b

+9bc−27d+3

√

−b

+4c

+4b

d−18bcd+27d

)

(1/3)

(3×2

(1/3)

)

x =











−(b/3) +

((1+i

√

3)(−b

+3c))

(3×2

(2/3)

(−2b

+9bc−27d+3

√

−b

+4c

+4b

d−18bcd+27d

)

(1/3)

)

−

((1−i

√

3)(−2b

+9bc−27d+3

√

−b

+4c

+4b

d−18bcd+27d

)

(1/3)

)

(6×2

(1/3)

)

x =











−(b/3) +

((1−i

√

3)(−b

+3c))

(3×2

(2/3)

(−2b

+9bc−27d+3

√

−b

+4c

+4b

d−18bcd+27d

√

)

(1/3)

)

−

((1+i

√

3)(−2b

+9bc−27d+3

√

−b

+4c

+4b

d−18bcd+27d

)

(1/3)

)

(6×2

(1/3)

)

In general, if ξ

, ξ

are the roots of a cubic polynomial, the discriminant D can

de deﬁned as

D = (ξ

− ξ

)

(ξ

− ξ

)

(ξ

− ξ

)

, (3.15)

and computed from the coeﬃcients a, b, c, d to infer on the nature of the roots. Con-

sidering a = 1, [235, p. 156, Exercise 10.17] gives the formula of the discriminant

D from the coeﬃcients b, c, d as

D = 18bcd − 4b

d + b

− 4c

− 27d

. (3.16)

If D > 0 then the roots of the cubic polynomial are real and distinct. If D < 0,

then one of the roots is re al and the remaining two are non real complex conjugate.

In a case where D = 0, multiple roots all which are real are given. In case the

coeﬃcients b, c, d are all positive, then all the three roots will be negative, while if

b, d are negative and c positive, all the roots will be p ositive.

3-63 Quartic polynomials

Quartic polynomials are those of degree 4. In a case where one ro ot ξ

exist for a

polynomial p(x) = 0, the division algorithm can be applied to obtain the factor

(x − ξ

)f(x). Here, f(x) is a cubic polynomial that can be s olved as discussed in

Sect. 3-62 to give at least one real root. The quartic polynomial ax

+ bx

+ cx

dx + e = 0 therefore has at least two real roots. The following conditions may

apply for a quartic p olynomial:

• p(x) has four real roots.

• p(x) has two real roots and two complex conjugate ro ots .

• p(x) has no real roots.

3-7 Methods for investigating roots 27

The solution of a quartic polynomial proceeds via substitution approach in-order

to reduce it. Considering a case where a = 1, the quartic polynomial x

+bx

+cx

dx+e = 0 is reduced by substituting x = z+a, with a ∈ R, to Z

+CZ

+EZ +F =

0 which is solved for g(Z) = 0. The solutions of g(Z) = 0 satisﬁes those of p(x) = 0

(see Sect. 3-5). Z

+ CZ

+ EZ + F = 0 is called the reduced quartic polynomial

which can be solved as discussed by [235, pp. 159-166].

Solution of the roots of quartic polynomials using Computer algebra software

of Matlab and Mathematica is as follows:

• Matlab: x = roots

([a b c d e])

, where

[a b c d e]

is a vector containing the

coeﬃcients in the ﬁeld R of reals. The quadratic equation can also be solved

using the solve comm and, e.g., solve(

+ bx

+ cx

+ dx + e = 0, x

)

• Mathematica: x = Root[f, k], where f is the quartic equation and k the k

root. The quadratic equation can als o be solved using the solve command, e.g.,

Solve[ax

+ bx

+ cx

+ dx + e == 0, x]. In the accompanying CD, one of the

Mathematica solution when a = 1 is presented.

In general, if ξ

, ξ

are the roots of a quartic polynomial, the discriminant

D can de deﬁned as

D = (ξ

− ξ

)

(ξ

− ξ

)

(ξ

− ξ

)

(ξ

− ξ

)

(ξ

− ξ

)

(ξ

− ξ

)

, (3.17)

and computed from the coeﬃcients b, c, d, e to infer on the nature of the roots.

Considering a = 1, [235, p. 171] gives the formula of the discriminant D from the

coeﬃcients b, c, d, e as

D =







18bcd

+ 18b

cde − 80bc

de − 6b

e + 144cd

+144b

− 128c

− 192bde

+ b

− 4b

− 4c

−4b

e + 16c

e − 27d

− 27b

+ 256e

(3.18)

If D > 0 then all the roots of the quartic polynomial are real and distinct or all

the four roots are pairs of non real complex conjugates. If D < 0, then two roots

are real and distinct while the other two are complex conjugates. For a case where

D = 0, at least two of the ro ots coincide.

3-7 Methods for investigating roots

3-71 Logarithmic and contour plot s on complex plane

Here we introduce two graphical and an algebraic - numeric m ethod to ﬁnd roots

of polynomials. Let us c onsider the following polynomial

f = −2829 + 65593z − 228035z

+ 536375z

− 295200z

+ 222000z

28 3 Basics of polynomial theory

ReHzL

ImHzL

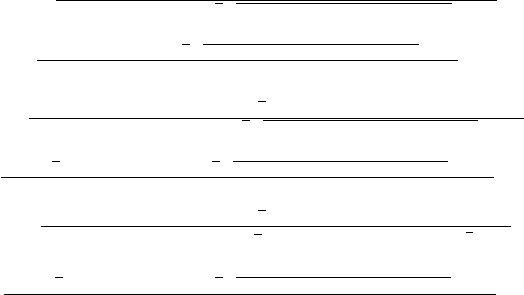
Figure 3.3. The surface of the function log(abs(f(z)) + 1) on the complex plane

Plotting the logarithmic of the absolute value of f (z)+1 on the complex plane leads

to Fig. 3.3. The additive constant is used to avoid singularity at abs(f(z)) = 0.

The “holes” on the surface show the approximate positions of the roots. To get

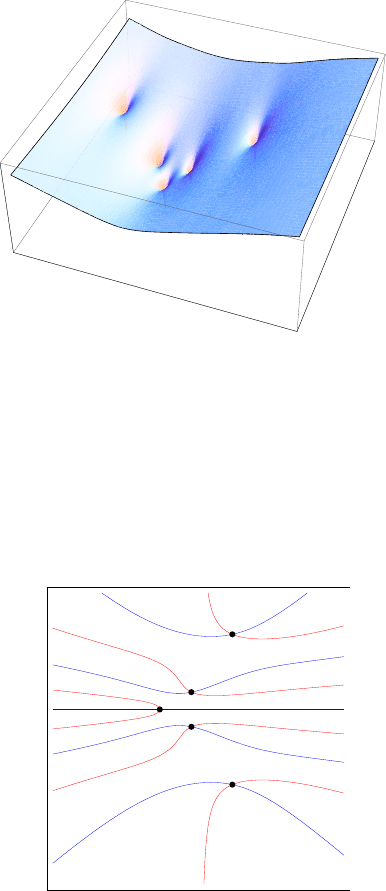
better approximation, we can display Re(f(z)) = 0 and Im(f(z)) = 0 contours

on the complex plane in Fig. 3.4. The cross points of these contours represent

locations of the roots.

ReHzL

ImHzL

Figure 3.4. The contour plot of f(z) on the complex plane. Along the lines the real

and imaginary parts are zero

3-7 Methods for investigating roots 29

3-72 Isograph simulator

Let us consider the exponential form of the complex numbers z = r

exp(iφ)

, and

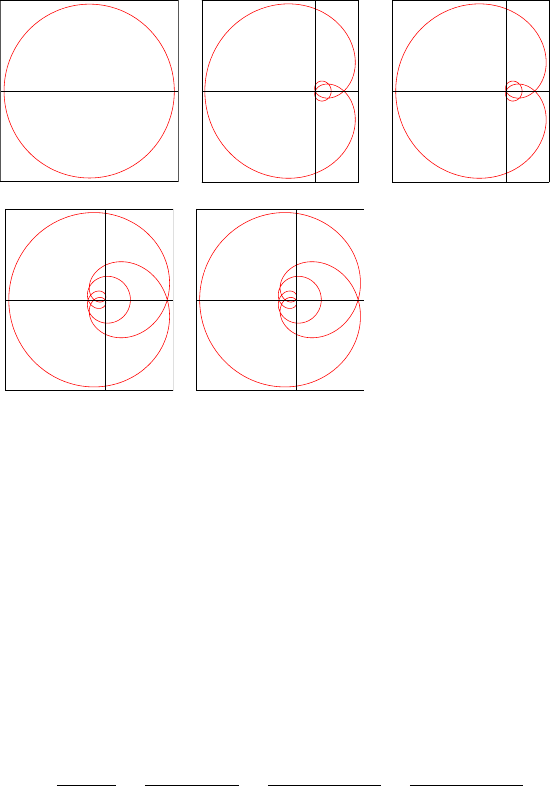
display f(z) as function of φ at constant r. Changing r values, ﬁnd the proper r

value at which the curve of f(z) crosses the origin of the coordinate system of the

complex plane (0, 0). The function IsoGraphSimulator in Mathematica simulates

this process. The numerical values of the roots are computed via NSolve and are

as presented in Fig. 3.5.

ÈxÈ=0.051165

ÈxÈ=0.213937 + 0.29782 I

ÈxÈ=0.213937 - 0.29782 I

ÈxÈ=0.425345 + 1.29279 I

ÈxÈ=0.425345 - 1.29279 I

Figure 3.5. The contour plot of f(z) on the complex plane. Along the lines the real

and imaginary parts are zero

3-73 Application of inverse series

We consider the x = r(y), as the inverse mapping of y = f(x). Then the roots of

f(x) can be computed as r(0), while f(r(0)) = 0. In order to illustrate the idea

let us consider the power series expansion for following second order polynomial,

about the point x = 0 to order four,

y = f (x) = c + bx + ax

The inverse series provides the approximation of the inverse function r(y),

r(y) =

(y − c)

−

(a(y − c)

)

(2a

(y − c)

)

−

(5a

(y − c)

)

The r(0) gives the root of the polynomial f(x) as

30 3 Basics of polynomial theory

r(0) = −

−

One may recognize that the (k + 1)

h term can be expressed as

−

−1−2k

1+k

Binomial[2k, k]

1 + k

indeed, for example, considering the ﬁrst four terms, we get

−

However, with inﬁnity terms we get the analytical solution,



−1 +

−4ac



Now we can apply this metho d to the polynomial considered as an example,

f(x) = −2829 + 65593z − 228035z

+ 536375z

− 295200z

+ 222000z

whose inverse is

r(y) = 0.0000152455(y + 2829.) + 8.08033 × 10

−10

(y + 2829.)

5.66776 × 10

−14

(y + 2829.)

+ 3.91367 × 10

−18

(y + 2829.)

+ 2.14685 × 10

−22

(y + 2829.)

2.00147 × 10

−27

(y + 2829.)

− 1.89902 × 10

−30

(y + 2829.)

− 3.98433 × 10

−34

(y + 2829.)

−

5.76614 × 10

−38

(y + 2829.)

− 6.85252 × 10

−42

(y + 2829.)

− 6.79426 × 10

−46

(y + 2829.)

−

5.16349 × 10

−50

(y + 2829.)

− 1.66894 × 10

−54

(y + 2829.)

+ 3.69854 × 10

−58

(y + 2829.)

1.05096 × 10

−61

(y + 2829.)

+ 1.77627 × 10

−65

(y + 2829.)

+ 2.38232 × 10

−69

(y + 2829.)

2.64939 × 10

−73

(y + 2829.)

+ 2.32786 × 10

−77

(y + 2829.)

+ 1.18834 × 10

−81

(y + 2829.)

One of the real root is

r(0) = 0.051165

Using this root, we can reduce the order of our polynomial to a quartic. For further

details, see Chap. 2 of the accompanying CD.

3-8 Computation of zeros of polynomial systems

In one variable case, the polynomial,

p(x) = a

+ a

d−1

(d−1)

+ . . . + a

+ a

x + a

has d roots, counting multiplicities, in the ﬁeld C of complex numbers according to

the fundamental theorem of algebra. However in multivariable case, the situation

is more complicated. To keep the discussion easy and transparent, we consider a

system of two p olynomials. Let us consider the following system,

G = a

+ a

x + a

xy + a

H = b

+ b

y + b

3-8 Computation of zeros of polynomial sys tems 31

Theorem 3.2 (B´ezout’s Theorem). Consider two polynomial equations in two

unknowns: g(x, y) = h(x, y) = 0. If this system has only ﬁnitely many zeros (x, y) ∈

, then the number of zeros is at most deg(g) ∗ deg(h). Here deg(g) and deg(h)

are the total degree of g(x,y) and h(x,y), respectively, see Sect. 3-1

These two polynomials have precisely four distinct zeros (x, y) ∈ C

for generic

choices of coeﬃcients a

and b

. It means that a certain polynomial in the coeﬃ-

cients a

, b

, called the discriminant, should be non- zero. The discriminant can be

computed via the function Resultant, which is zero if and only if the polynomials

have a common root, see details in Chapter 5.

B´ezout’ s theorem would predict 2 ∗ 3 = 6 common complex zeros for our

system. Indeed, in projective geometry we would expect the cubic curve (G = 0)

and the quadratic curve (H = 0) to intersect in six points. However, the system

has actually 4 common roots. To understand why is four and not six let us consider

convex polygons associated with our system. A polytope is a subset of R

which is

the convex hull of a ﬁnite set of points. A 2-dimensional polytope is called polygon.

Consider a polynomial f(x, y),

f(x, y) = a

+ a

+ . . . + a

This is a polygon in R

having at most m vertices. In general, every polynomial

in n unknowns can be represented by a Newton polytope in R

. Let us consider

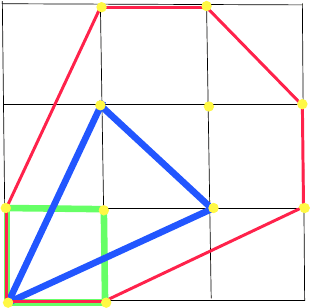
the Newton polygons of our systems. The Newton p olygon of the polynomial G is

quadrangel with points (0,0), (1,0),(1,1) and (0,1), while that of the polynomial

H is a triangle (0,0), (2,1), (1,2), see Fig. 3.6.

Figure 3.6. Mixed area of Newton-polygons of the two polynomials

The Minkowski sum of the two polygons, P and Q in the plane is

32 3 Basics of polynomial theory

P + Q = p + q : p ∈ P, q ∈ Q

The Newton p olygon of the product of two polynomials is the Minkowski sum of

the Newton polyon of these two polynomials, namely

New(G ∗ H) = N ew(G) + N ew(H)

The corresponding points can be seen on Fig. 3.6. So the Minkowski sum of the

polygons mirrors the algebraic operation of multiplying polynomials. If P and Q

ar any two polynomials then their mixed area can be deﬁned as it follows.

M(P, Q) = area(P + Q) − area(P ) −area(Q)

In our case,

M(New(G), New(H)) =

− 1 −

= 4

This number coincides with the number of common zeros of G and H. This is not

an accident, but is an instance of the general theorem of Bernstein.

Theorem 3.3 (Bernstein’s Theorem). If G and H are two generic bivariate

polynomials, then the number of non-zero solutions of G(x, y) = H(x, y) = 0 ∈ C

equals the mixed area M(New(G), New(H)).

Elimination theory deals with the problem of eliminating one or more variables

from a system of polynomial equations, thus reducing the problem to a smaller

problem in fewer variables. For instance, if we wish to solve,

U = a

+ a

x + a

; V = b

+ b

x + b

for U = V = 0 with a

6= 0 and b

6= 0, we can eliminate the variable x to get a

polynomial of degree 4 which is the resultant. This resultant vanishes if and only

if the given quadratic polynomials have common c omplex root x. This resultant

method can be extended for case n > 2 and various determinants formulae are

known for multivariate resultant, see Chap. 5. Other approaches include Groebner

basis and homotopy which are discussed in the Chaps. 4 and 7 respectively.

3-9 Concluding remarks

What we have presented is just a nutshell of the topic “polynomials”. Several

books, e.g., [55, 298, 335, 436] are dedicated speciﬁcally to it.

4 Groebner basis

“There are no good, general methods for solving systems of more than one

nonlinear equation. Furthermore, it is not hard to see why (very likely)

there never will be any good, general methods:...” W. H. Press et al.

4-1 The origin

This chapter presents you the reader with one of the most powerful computer

algebra to ols, besides the polynomial resultants (discussed in the next chapter),

for solving nonlinear systems of equations which you may encounter. The basic

tools that you will require to develop your own algorithms for solving problems

requiring closed form (exact) solutions are presented. This powerful tool is the

“Gr¨obner basis” written in English as Groebner basis. It was ﬁrst suggested by B.

Buchberger in 1965, a PhD student of Wolfgang Groebner (1899 - 1980). Groebner,

already in 1949, had suggested a method for ﬁnding a linearly independent basis

of the vector space of the residue class ring of the polynomial ring modulo a

polynomial ideal. In studying termination of this method, Buchberger came up

both with the notion of Groebner bases (certain generating sets for polynomial

ideals) and with an always terminating algorithm for computing them. In 1964,

H. Hironaka (1931-) had indep e ndently introduced an analogous notion for the

domain of power series in connection with his work on resolution of singularities

in algebraic geometry and named it standard basis [262, p. 187]. However, he did

not give any method for computing these bases. B. Buchberger decided to honour

his thesis supervisor W. Groebner by naming the standard basis for Ideals in

polynomial rings k [x

, . . ., x

] as Groebner basis [95].

In this book, as in modern books, we will adopt the term Groebner basis

and present the subject in the simplest form that can easily be understood from

geodetic as well as geoinformatics perspective.

As a recipe, consider that most problems in nature, here in geodesy, geoin-

formatics, machine vision, robotics, surveying etc., can be modelled by nonlinear

systems of equations. Let us consider a simple case of planar distance measure-

ments in Fig. 4.1. Equations relating these measured distances to the co ordinates

of an unknown station were already presented in Sect. 3-4. In that section, we did

relate the me asured distances {s

, i = 1, 2} to the coordinates of the unknown

station by (3.5) and (3.6). We stated that the intersection of these two equations

lead to univariate polynomials whose solution give the desired position of an un-

known station. We did not however give any explanation on how the univariate

polynomials are derived from the set of multivariate quadratic polynomials (3.5)

and (3.6). The derivation of the univariate polynomials from systems of nonlin-

ear equations form one of the major tasks of Groebner basis. Let us denote the

distance {s

, i = 1, 2} by {d

, i = 1, 2} and re-write (3.5) and (3.6) respectively as

= (x

− x

)

+ (y

− y

)

(4.1)

and

J.L. Awange et al., Algebraic Geodesy and Geoinformatics, 2nd ed.,

DOI 10.1007/978-3-642-12124-1 4,

 Springer-Verlag Berlin Heidelberg 2010