Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


SINGULAR INTEGRALS
309
Table 5.22 Examples
of
Gauss-Laguerre quadrature
Nodes
2
4
8
16
32
64
J(l)-
J~l)
l.OlE-
4
1.28E-
5
-9.48E-
8
3.16E
-11
7.11E-
14
J(2)-
J!2)
-8.05E-
2
-4.20E-
2
1.27E-
2
-1.39E-
3
3.05E-
5
1.06E-
7
J<3l -
1~3)
7.75E-
2
6.96E-
2
3.70E-
2
1.71E-
2
8.31E-
3
4.07E-
3
Gauss-Laguerre quadrature
is
best for integrands that decrease exponentially as
x--+
oo.
For
integrands that are
0(1fxP),
p > 1, as x--+
oo,
the convergence
rate becomes quite poor
as
p
--+
1.
These comments are illustrated in Table 5.22.
For a formal discussion of the convergence of Gauss-Laguerre quadrature, see
Davis and Rabinowitz
(1984, p. 227).
One especially easy case of Gaussian quadrature
is
for the singular integral
f
l
f(x)
dx
I(!)=
-1/1-
xz
(5.6.12)
With this weight function, the orthogonal polynomials are the Chebyshev poly-
nomials
{Tn(x),
n
~
0}. Thus the integration nodes in (5.6.10) are given by
(
2j-
1 )
xj,n
=cos
2
n
'IT
j = 1,
...
, n
and from (5.3.11), the weights are
'IT
w.
=-
J,n
n
j=1,
...
,n
(5.6.13)
Using the formula (5.3.10) for the error, the Gaussian quadrature formula for
(5.6.12) is given by
(5.6.14)
for some - 1 <
11
<
1.
This formula
is
related to the composite midpoint rule (5.2.18). Make the
change of variable
x = cos
()
in (5.6.14) to obtain
w
'IT
n
1 !(cos
0)
dO=
- E !(cos
oj,n)
+ E
o n
j=l
(5.6.15)
where
Oj,
n =
(2
j -
1)'1T
j2n.
Thus Gaussian quadrature for (5.6.12)
is
equivalent
to the composite midpoint rule applied to the integral on the left in
(5.6.15). Like

310
NUMERICAL
INTEGRATION
the trapezoidal rule, the midpoint rule has an error expansion very similar to that
given in (5.4.9) using the Euler-MacLaurin formula. The Corollary 1 to Theorem
5.5 also
is
valid, showing the composite midpoint rule to be highly accurate for
periodic functions. This
is
reflected in the high accuracy of (5.6.14). Thus
Gaussian quadrature for (5.6.12) results in a formula that would have been
reasonable from the asymptotic error expansion for the composite midpoint rule
applied to the integral on the left of (5.6.15).
Analytic treabnent of
singularity Divide the interval of integration into two
parts, one containing the singular point, which
is
to be treated analytically.
For
example, consider
I
=.foh!(x)log(x)
dx =
[{
+
J.h]/(x}log(x}
dx = /
1
+ /
2
(5.6.16)
Assuming
f(x)
is smooth on
[t:,
b], apply a standard technique to the evaluation
of
/
2
•
For
/(x)
about zero, assume it has a convergent Taylor series
on
[0,
t:].
Then
(
((
00
)
1
1
=
lt(x)log(x)
dx
= 1
,Eajxj
log(x)
dx
0 0 0
00
(j+
1 [ 1 ]
=:[a.--
log(t:)-
--
o
lj+1
j+1
For
example, with
define
1
4,.
I = cos (
x)
log (
x)
dx
0
1
1
= L
1
cos(x)log(x)
dx
0
( =
.1
(5.6.17)
(3
[ 1 ]
£5
[ 1 ]
=
t:[
log (
t:)
-
1]
- - log (
t:)
- - + - log (
t:)
- - - · · ·
6 3 600 5
This
is
an alternating series, and thus
it
is clear
that
using the first three terms
will give a very accurate value for
/
1
•
A standard method can
be
applied to /
2
on
[.1,
4'1T].
Similar techniques can be used with infinite intervals of integration
[a,
oo
),
discarding the integral over [b,
oo)
for some large value
of
b. This is
not
developed here.
Product integration Let
/(/)
=
J:w(x)f(x)
dx
with a near-singular
or
singu-
lar weight function
w(x)
and a smooth function
f(x).
The
main idea is to

SINGULAR INTEGRALS
311
produce a sequence of functions fn(x) for which
1.
II/-
fnlloo
= Max
IJ(x)-
fn(x)l
__.
0
a:;;x:;;b
2. The integrals
In(!)=
J.bw(x)fn(x)
dx
a
(5.6.18)
can be fairly easily evaluated.
This generalizes the schema
(5.0.2) of the introduction.
For
the error,
II(!)-
In(!)
I~
J.biw(x)IIJ(x)-
fn(x)jdx
a
~II/-
!niL,.,
fi
w(x)
I dx
a
(5.6.19)
Thus
In(/)
__.
!(f)
as
n
---.
oo,
and the rate of convergence is at least
as
rapid
as
that
of
fn(x)
to
f(x)
on
[a,
b].
Within the preceding framework, the product integration methods are usually
defined by using piecewise polynomial interpolation to define fn(x) from
f(x).
To illustrate the main ideas, while keeping the algebra simple,
we
will define the
product trapezoidal method for evaluating
I(!)=
fobJ(x)log(x)
dx
(5.6.20)
Let
n
~
1, h =
bjn,
xj
=
jh
for j =
0,
1,
...
, n. Define fn(x) as the piecewise
linear function interpolating to
f(x)
on the nodes x
0
,
x
1
,
...
, xn. For
xj-l
~
x
~
xj,
define
(5.6.21)
for j = 1, 2,
...
, n. From (3.1.10), it is straightforward to show
h2
Ill-
fnlloo
~
sllf"lloo
(5.6.22)
provided
f(x)
is
twice continuously differentiable for 0
~
x
~
b.
From (5.6.19)
we obtain the error bound
(5.6.23)
This method of defining
/n(/)
is
similar to the regular trapezoidal rule (5.1.5).
The rule (5.1.5) could also have been obtained by integrating the preceding
function fn(x),
but
the weight function would have been simply
w(x)
=
1.
We

i -··- -······
312 NUMERICAL INTEGRATION
can easily generalize the preceding by using higher degree piecewise polynomial
interpolation. The use of piecewise quadratic interpolation to define
/,(x)
leads
to a formula
/,(/)
called the product
Simpson's
rule. And using the same
reasoning as led to
(5.6.23), it can be shown that
(5.6.24)
Higher order formulas can be obtained by using even higher degree interpolation.
For
the computation
of/,(/)
using (5.6.21),
1
Jx
1
w
0
=-
(x
1
-
x)Iog(x)
dx
h x
0
1
JX·
wj
= h
1
(x-
xj_
1
)
log
(x)
dx
.
Xj-1
1
1
xj+l
+-
(xj+
1
-
x)
log(x)
dx
h
xj
(5.6.25)
j=1,
...
,n-1
(5.6.26)
The calculation of these weights can be simplified considerably. Making the
change
of
variable
x-
xj_
1
= uh, 0
.:5;
u
.:5;
1,
we have
1
JX·
11
-
1
(x-
xj_
1
)
log(x)
dx
= h u
log[{J-
1 +
u)h]
du
h
xj-l
0
h
11
= - log
(h)
+ h u log
(J
- 1 +
u)
du
2 0
and
1
JX·
11
-
1
( x j -
x)
log ( x)
dx
= h ( 1 -
u)
log [
(j
- 1 +
u)
h] du
h
Xj-l
. 0
h
11
= - log (h) + h ( 1 - u) log
(j
- 1 +
u)
du
2 0
Define
,h(k)
= f(l-
u)
log(u
+
k)
du
(5.6.27)
----~--------------·-·-
----·---------- -
--
I
SINGULAR INTEGRALS 313
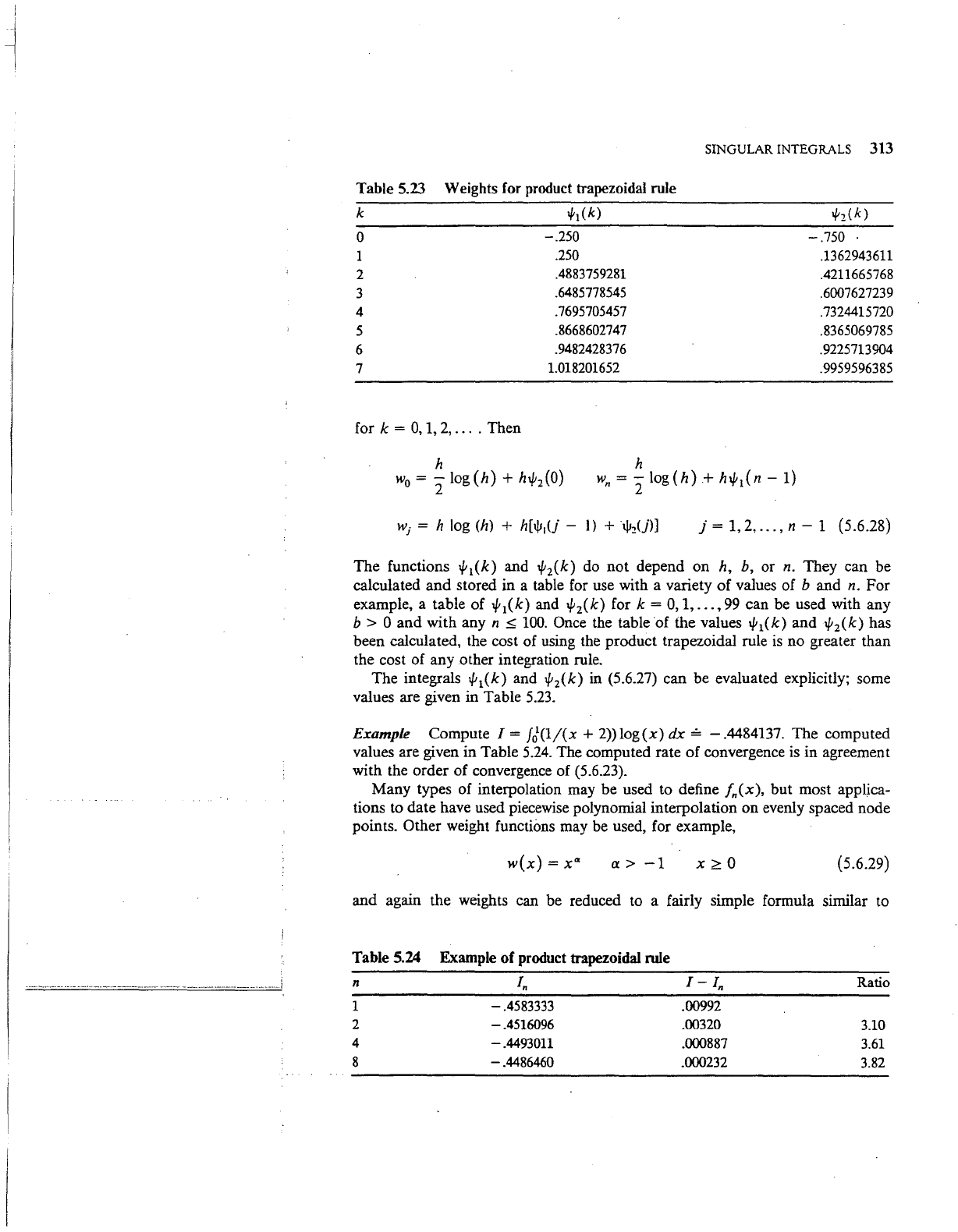
Table 5.23
Weights for product trapezoidal rule
k
1/tl
(k)
l/t2
(
k)
0
-.250
-.750
.
.
250
.1362943611
2
.4883759281
.4211665768
3
.6485778545
.6007627239
4
.7695705457
.7324415720
5
.8668602747
.8365069785
6
.9482428376
.9225713904
7
1.018201652 .9959596385
for k =
0,
1,
2,
....
Then
h
h
w
0
= 2
log
(h) + h
th
(
0)
w"
=
2log(h)
+
hth(n-
1)
j = 1, 2,
...
, n - 1 (5.6.28)
The functions
th(k)
and
th(k)
do not depend on
h,
b,
or n. They can be
calculated and stored in a table for use with a variety of values of
b and n. For
example, a table of
th(k)
and
l[;
2
(k)
fork=
0,
1,
...
,99
can be used with any
b > 0 and with any n
~
100.
Once the table of the values
l[;
1
(k)
and
l[;
2
(k)
has
been calculated, the cost of using the product trapezoidal rule
is
no greater than
the cost of any other integration rule.
The integrals
t/;
1
(k)
and
th(k)
in (5.6.27) can be evaluated explicitly; some
values are given in Table
5.23.
Example Compute
I=
Jl(lj(x
+
2))log(x)
dx
= -.4484137. The computed
values are given in Table
5.24.
The computed rate of convergence
is
in agreement
with the order of convergence of (5.6.23).
Many types of interpolation may be used to define
fn(x),
but most applica-
tions to date have used piecewise polynomial interpolation on evenly spaced node
points.
Other weight functions may be used, for example,
w(x) =
xa
a>
-1
x~O
(5.6.29)
and again the weights can be reduced to a fairly simple formula similar to
Table 5.24
Example
of
product trapezoidal rule
n
I"
I-
In
Ratio
1 -.4583333 .00992
2
-.4516096
.00320
3.10
4
-.4493011
.000887
3.61
8
-.4486460
.000232
3.82

!
I
j
I
·---·-·--
_
_j
314
NUMERICAL INTEGRATION
(5.6.28). For an irrational value of a, say
1
w(x)
=
---;.r-
xv2
-1
a change of variables can no longer be used to remove the singularity in the
integraL Also, one of the major applications
of
product integration
is
to integral
equations in which the kernel function has
an
algebraic
andjor
logarithmic
singularity. For such equations, changes of variables are no longer possible, even
with square root singularities.
For
example, consider the equation
i\
(x)
-
-~b
fP(Y)
dy
=
f(x)
fP
a
lx-
Yl
112
with i\, a,
b,
and f given and
fP
the desired unknown function. Product
integration leads to efficient procedures for such equations, provided fP(Y)
is
a
smooth function
[see Atkinson (1976), p. 106].
For complicated weight functions in which the
wei~ts
wj
can no longer be
calculated, it is often possible to modify the problem to one in which product
integration is still easily applicable. This
will
be examined using
an
example.
Example Consider
I=
/
0
/(x)
log(sin
x)
dx.
The
integrand has a singularity at
both
x = 0 and x =
'TT.
Use
[
sin(x)]
log (sin
x)
=
log
x
(.,
_
x)
+ log (
x)
+ log
(.,
-
x)
and this gives
I=
fo"t(x) log [
x(
:n_x
x)]
dx
+
{'t(x)
log
(x)
dx
+
fo"t(x)log(.,-
x)
dx
(5.6.30)
Integral /
1
has an infinitely differentiable integrand, and any standard numerical
method will perform
welL
Integral I
2
has already been discussed, with
w(x)
=
log(x).
For
I
3
,
use a change of variable to write
I
3
=
1"t(x)1og(.,-
x)
dx
=
1"t(.,-
z)log(z)
dz
0 0
Combining with I
2
,
I2
+
I3
=
fo"log{x)[f(x)
+
/(.,-
x)]
dx

NUMERICAL DIFFERENTIATION 315
to
which the preceding work applies. By such manipulations, the applicability
of
the
cases
w(x)
= log.(x) and
w(x)
= X
0
is
much
greater
than might first
be
imagined.
For
an
asymptotic error analysis
of
product
integration; see the work
of
de
Hoog
and
Weiss (1973), in which some generalizations
of
the
Euler-
MacLaurin
expansion are derived. Using their results, it can
be
shown
that
the
error
in the
product
Simpson rule is
0(
h
4
log
(h)).
Thus
the
bound
(5.6.24) based
on
the
interpolation error
f(x)
- fn(x) does
not
predict the correct rate·
of
convergence. This is similar to the result (5.1.17) for the Simpson rule error, in
which the
error
was smaller than the use
of
quadratic
interpolation would lead
us
to believe.
5.7 Numerical Differentiation
Numerical
approximations to derivatives are used mainly in two ways. First, we
are
interested in calculating derivatives
of
given
data
that are often
obtained
empirically. Second, numerical differentiation formulas are used in deriving
numerical methods for solving ordinary
and
partial
differential equations.
We
·begin this section by .deriving some
of
the most commonly used formulas for
numerical differentiation.
The
problem
of
numerical differentiation
is
in
some ways more difficult
than
that
of
numerical integration. When using empirically determined function
values, the
error
in these values will usually
lead
to instability in the numerical
differentiation
of
the function. In contrast, numerical integration is stable when
faced with such errors (see
Problem 13).
The
classical fonnulas One
of
the main
approaches
to deriving a numerical
approximation
to
f'(x)
is to use the derivative
of
a polynomial Pn(x)
that
interpolates
f(x)
at
a given set
of
node points.
Let
x
0
,
x
1
,
•••
,
xn
be
given,
and
let
Pn(x) interpolate
f(x)
at these nodes. Usually {X;} are evenly spaced.
Then
use
f'(x)
=
p~(x)
From
(3.1.6), (3.2.4),
and
(3.2.11):
n
Pn(x)
= L
f(x)l/x)
j-0
1/x)
=
i'n(x)'
(x-
x)i'n(x)
(5.7.1)
(x
-,x
0
) • • •
(x-
xj_
1
)(x-
xj+l) · · ·
(x-
xn)
(xj-
x
0
) • • •
(xj-
xj_
1
)(xj-
xj+l) · · ·
(xj-
xJ
'~'n(x)
=
(x-
x
0
) • • •
{x-
xn)
f{x)-
Pn(x)
=
'~'n(x)f[xo,···•
Xn,
x}
(5.7.2)

316 NUMERICAL INTEGRATION
Thus
II
f'(x)
=
p~(x)
= L
f(x)IJ(x)
=
Dhf(x)
j=O
f'(x)-
Dhf(x)
=
ir:(x)J[x
0
,
..•
,
x,,
x]
+i',{x
)/[x
0
,
•••
,
x,,
x,
x]
with the last step using (3.2.17). Applying (3.2.12),
(5.7.3)
(5.7.4)
with
~
1
,
~
2
E
£'{
x
0
,
...
,
x,,
x
}.
Higher order differentiation formulas and their
error can
be
obtained by further differentiation
of
(5.7.3)
and
(5.7.4).
The most common application of the preceding is to evenly spaced nodes
{
x;}. Thus let
X;=
X
0
+
ih
i
~
0
with h >
0.
In
this case, it
is
straightforward to show
that
Thus
We
now
derive examples of each case.
ir;(x)=FO
v;(x)
= 0
{5.7.6)
(5.7.7)
Let n =
1,
so that p,(x)
is
just the linear interpolate of
(x
0
,
f(x
0
))
and
(x
1
,
f(x
1
)).
Then (5.7.3) yields
(5.7.8)
From (5.7.5),
(5.7.9)
since
i'(x
0
)
=
0.
To
improve on this with linear interpolation, choose x = m =
(x
0
+ x
1
)j2.
Then

NUMERICAL DIFFERENTIATION 317
We usually rewrite this by letting 8 =
h/2,
to
obtain
1
/'(m)
~
Dsf(m) =
28
[/(m
+
8)-
J(m-
8)]
(5.7 .10)
For
the error, using (5.7.5) and
ir{(m)
= 0,
m-
8 5:
~
2
5: m + 8 (5.7.11)
In
general, to obtain the higher order case in (5.7.7), we
want
to choose the nodes
{X;}
to have
'~':(x)
= 0. This will be true if n is
odd
and
the nodes are placed
symmetrically about x, as in (5.7.10).
To
obtain higher order formulas in which the nodes all lie on one side
of
x,
use higher values
of
n in (5.7.3).
For
example, with x = x
0
and n =
2,
(5.7.12)
(5.7.13)
The method
of
undetermined coefficients
Another
method to derive formulas
for numerical integration, differentiation,
and
interpolation is called the method
of
undetermined coefficients.
It
is
often equivalent
to
the formulas obtained from
a polynomial interpolation formula,
but
sometimes
it
results in a simpler deriva-
tion. We will illustrate the method by deriving a formula for
f"(x).
Assume
f"(x)
~
D~
2
>J(x)
=
Af(x
+h)+
Bf(x.)
+
Cf(x-
h)
(5.7.14)
with A, B,
and
C unspecified. Replace
f(x
+h)
and
f(x-
h)
by the Taylor
expansions
with x - h
5:
L
5:
x 5:
~
+
5:
x +
h.
Substitute into (5.7.14) and rearrange
into
a polynomial in powers of h:
Af(x
+h)+
Bf(x)
+
Cf(x-
h)
h2
=(A+
B +
C)f(x)
+
h(A-
C)f(x)
+-(A+
C)f"(x)
2
(5.7.15)

318 NUMERICAL INTEGRATION
In
order
for this to equal
f"(x),
we set
A+B+C=O
A-
C=O
2
A
+C=-
h2
The solution
of
this system
is
This yields the formula
1
A
=C=-
h1
-2
B=-
h1
D<
1
>J(
x)
=
_J(_x_+_h_)_-_2/_(_x
)_+_f(_x_-_h_)
h
h1
.
(5.7.16)
(5.7.17)
For
the error, substitute (5..7.16) into (5.7.15)
and
use (5.7.17). This yields
Using Problem 1
of
Chapter 1, and assuming
f(x)
is four times continuously
differentiable,
(5.7.18)
for some
x-
h
~
~
~
x
+h.
Formulas (5.7.17) and (5.7.18) could have been
derived by calculating
p2'(x)
for the quadratic polynomial interpolating
f(x)
at
x - h,
x,
x + h,
but
the preceding
is
probably simpler.
The
general idea
of
the method
of
undetermined coefficients is to choose the
Taylor coefficients in an expansion in h so as to obtain the desired derivative (or
integral) as closely as possible.
Effect of
error
in function values The preceding formulas are useful when
deriving methods for solving ordinary
and
partial differential equations,
but
they
can lead to serious errors when applied to function values that are obtained
empirically.
To
illustrate a method for analyzing the effect
of
such errors, we
consider.
the
second derivative approximation (5.7.17).
Begin by rewriting (
5.
7 .17) as
with
xj
= x
0
+
jh.
Let the actual values used
be[;
with
J(x;) =
[;
+
f.;
i = 0,
1,2
(5.7.19)
