Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


318 Chapter 5
Substituting this equation into the preceding solution yields
> f(r)=subs(theta=0,u(r,theta));
(r −1)(2 −r) =
∞
n=1
√
2 sin
nπ ln(r)
ln(2)
B(n) sinh
1
2
nπ
2
ln(2)
√
ln(2)
(5.124)
This equation is the Fourier series expansion of f(r) in terms of the orthonormal
Sturm-Liouville eigenfunctions found earlier. To evaluate the Fourier cofficients, we take the
inner product of both sides with respect to the orthonormal eigenfunctions, and, taking
advantage of the previous statement of orthonormality, we get, for n = 1, 2, 3,...,
> B(n):=(1/sinh(n*Pi*b/ln(a)))*Int(f(r)*R[n](r)*w(r),r=1..a);B(n):=simplify(value(%)):
B(n) :=
2
1
(r −1)(2 −r)
√
2 sin
nπ ln(r)
ln(2)
√
ln(2)r
dr
sinh
1
2
nπ
2
ln(2)
(5.125)
> B(n):=simplify(subs({sin(n*Pi/2)=(exp(i*n*Pi/2)−exp(−i*n*Pi/2))/(2*i),cos(n*Pi/2)=
(exp(i*n*Pi/2)+exp(−i*n*Pi/2))/2},B(n))):B(n):=simplify(subs({exp(i*n*Pi)=(−1)ˆn,
exp(−i*n*Pi)=(−1)ˆn},B(n)));
B(n) :=
√
2ln(2)
5/2
(n
2
π
2
+10(−1)
1+n
n
2
π
2
−8ln(2)
2
+8ln(2)
2
(−1)
n
)
nπ sinh
1
2
nπ
2
ln(2)
n
4
π
4
+5n
2
π
2
ln(2)
2
+4ln(2)
4
(5.126)
Generalized series terms
> u[n](r,theta):=eval(R[n](r)*Theta[n](theta));
u
n
(r, θ) :=
2ln(2)
2
sin
nπ ln(r)
ln(2)
n
2
π
2
+10(−1)
1+n
n
2
π
2
−8ln(2)
2
+8ln(2)
2
(−1)
n
× sinh
⎛
⎝
nπ
1
2
π −θ
ln(2)
⎞
⎠
⎞
⎠
nπ sinh
1
2
nπ
2
ln(2)
n
4
π
4
+5n
2
π
2
ln(2)
2
+4ln(2)
4
(5.127)

The Laplace Par tial Differential Equation 319
Series solution
> u(r,theta):=Sum(u[n](r,theta),n=1..infinity);
u(r, θ) :=
∞
n=1
2ln(2)
2
sin
nπ ln(r)
ln(2)
n
2
π
2
+10(−1)
1+n
n
2
π
2
−8ln(2)
2
+8ln(2)
2
(−1)
n
× sinh
⎛
⎝
nπ
1
2
π −θ
ln(2)
⎞
⎠
⎞
⎠
πn sinh
1
2
nπ
2
ln(2)
n
4
π
4
+5n
2
π
2
ln(2)
2
+4ln(2)
4
(5.128)
First few terms of expansion
> u(r,theta):=sum(u[n](r,theta),n=1..5):
> cylinderplot([r,theta,u(r,theta)],r=1..a,theta=0..b,axes=framed,thickness=1);
0.2
0.25
0.15
0.1
0
0
0.5
y
z
1
22
1.5
1
x
0.5
0
1.5
0.05
Figure 5.8
The three-dimensional surface shown in Figure 5.8 depicts the electrostatic potential
distribution u(r, θ) over the cylindrical region. Note how the edges of the surface adhere to the
given boundary conditions. The equipotential lines can be obtained from Maple by clicking on
the figure, choosing the special option “Render the plot using the polygon patch and contour
style” in the graphics bar, and then clicking the “redraw” button.
EXAMPLE 5.7.4: We seek the steady-state temperature distribution in a thin cylindrical plate
over the domain D ={(r, θ) |0 <r<1, −π<θ<π} whose lateral surface is insulated. The
side r = 1 has a temperature distribution f(θ) given as follows, the solution is finite at r = 0,
and we force periodic boundary conditions on the angle θ.
SOLUTION: The homogeneous Laplace equation is
∂
∂r
u(r, θ) +r
∂
2
∂r
2
u(r, θ)
r
+
∂
2
∂θ
2
u(r, θ)
r
2
= 0
The boundary conditions are
|
u(0,θ)
|
< ∞ and u(1,θ)= sin(3θ)

320 Chapter 5
and
u(r, −π) = u(r, π) and u
θ
(r, −π) = u
θ
(r, π)
Here we see that the boundary conditions are periodic with respect to the θ variable.
Ordinary differential equations from the method of separation of variables are
d
2
dθ
2
(θ)+λ(θ) = 0
and
r
2
d
2
dr
2
R(r)
+r
d
dr
R(r)
−λR(r) = 0
Periodic conditions on the θ equation
(−π) = (π) and
θ
(−π) =
θ
(π)
Assignment of system parameters
> restart:with(plots):a:=1:
The allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Example 2.6.1. For n = 0,
> lambda[0]:=0;
λ
0
:= 0 (5.129)
For n = 1, 2, 3,...,
> lambda[n]:=nˆ2;
λ
n
:= n
2
(5.130)
Orthonormal eigenfunctions
For n = 1, 2, 3,...,
> phi[n](theta):=sqrt(1/Pi)*cos(n*theta);psi[n](theta):=sqrt(1/Pi)*sin(n*theta);phi[m](theta):=
subs(n=m,phi[n](theta)):psi[m](theta):=subs(n=m,psi[n](theta)):
φ
n
(θ) :=
cos(nθ)
√
π
ψ
n
(θ) :=
sin(nθ)
√
π
(5.131)
For n = 0,

The Laplace Par tial Differential Equation 321
> phi[0](theta):=1/sqrt(2*Pi);
φ
0
(θ) :=
1
2
√
2
√
π
(5.132)
Statement of orthonormality with respect to the weight function w(θ) = 1
> w(theta):=1:Int(phi[n](theta)*phi[m](theta)*w(theta),theta=−Pi..Pi)=delta(n,m);
π
−π
cos(nθ) cos(mθ)
π
dθ = δ(n, m) (5.133)
> Int(psi[n](theta)*psi[m](theta)*w(theta),theta=−Pi..Pi)=delta(n,m);
π
−π
sin(nθ) sin(mθ)
π
dθ = δ(n, m) (5.134)
Basis vectors for the r equation for λ>0
> r1(r):=rˆ(sqrt(lambda));r2(r):=rˆ(−sqrt(lambda));
r1(r) := r
√
λ
r2(r) := r
−
√
λ
(5.135)
General solution to the r equation for λ>0
> R[n](r):=C(n)*rˆ(sqrt(lambda))+D(n)*rˆ(−sqrt(lambda));
R
n
(r) := C(n)r
√
λ
+D(n)r
−
√
λ
(5.136)
Substituting into the r-dependent boundary condition and requiring a finite solution at r = 0
yields
> D(n):=0;
D(n) := 0 (5.137)
The r-dependent solution for n = 1, 2, 3,..., for the given eigenvalues, reads
> R[n](r):=rˆ(n);
R
n
(r) := r
n
(5.138)
Basis vectors for the r equation for λ = 0

322 Chapter 5
> r1(r):=1;r2(r):=ln(r);
r1(r) := 1
r2(r) := ln(r) (5.139)
General solution to the r equation for λ = 0is
> R[0](r):=A(0)+B(0)*ln(r);
R
0
(r) := A(0) +B(0) ln(r) (5.140)
Substituting into the r-dependent boundary condition at r = 0 yields
> B(0):=0;
B(0) := 0 (5.141)
The r-dependent solution for n = 0 reads
> R[0](r):=A(0);
R
0
(r) := A(0) (5.142)
Generalized series terms
> u[0](r,theta):=R[0](r)*phi[0](theta);u[n](r,theta):=R[n](r)*(A(n)*phi[n](theta)+B(n)*
psi[n](theta));
u
0
(r, θ) :=
1
2
A(0)
√
2
√
π
u
n
(r, θ) := r
n
A(n) cos(nθ)
√
π
+
B(n) sin(nθ)
√
π
(5.143)
Eigenfunction expansion
> u(r,theta):=u[0](r,theta)+Sum(u[n](r,theta),n=1..infinity);
u(r, θ) :=
1
2
A(0)
√
2
√
π
+
∞
n=1
r
n
A(n) cos(nθ)
√
π
+
B(n) sin(nθ)
√
π
(5.144)
Evaluation of Fourier coefficients from the specific remaining boundary condition
u(1,θ)= f(θ)
> f(theta):=sin(3*theta);
f(θ) := sin(3θ) (5.145)
Substituting this condition into the preceding solution yields

The Laplace Par tial Differential Equation 323
> f(theta)=subs(r=a,u(r,theta));
sin(3θ) =
1
2
A(0)
√
2
√
π
+
∞
n=1
A(n) cos(nθ)
√
π
+
B(n) sin(nθ)
√
π
(5.146)
This equation is the Fourier series expansion of f(θ) in terms of the orthonormalized
Sturm-Liouville eigenfunctions found earlier. To evaluate the Fourier cofficients, we take the
inner product of both sides with respect to the orthonormalized eigenfunctions, and, taking
advantage of the previous statement of orthonormality, we get, for n = 1, 2, 3,...,
> A(n):=(1/(aˆ(n)))*Int(f(theta)*phi[n](theta)*w(theta),theta=−Pi..Pi);A(n):=
expand(value(%)):
A(n) :=
π
−π
sin(3θ) cos(nθ)
√
π
dθ (5.147)
> A(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},A(n)));
A(n) := 0 (5.148)
> B(n):=(1/aˆn)*Int(f(theta)*psi[n](theta)*w(theta),theta=−Pi..Pi);
B(n) :=
π
−π
sin(3θ) sin(nθ)
√
π
dθ (5.149)
> B(n):=expand(value(%));
B(n) := −
6 sin(πn)
√
π(−9 +n
2
)
(5.150)
The only term that survives here is the n = 3 term, which is evaluated to be the limit of the
preceding equation:
> B(3):=limit(B(n),n=3);
B(3) :=
√
π (5.151)
Note that, because of the previous statement of orthonormality, only the n = 3 term survives.
We use the Kronecker delta to write the B(n) term as
> B(n):=B(3)*delta(n,3);
B(n) :=
√
πδ(n,3) (5.152)
For n = 0,
324 Chapter 5
> A(0):=Int(f(theta)*phi[0](theta)*w(theta),theta=−Pi..Pi);A(0):=value(%):
A(0) :=
π
−π
1
2
sin(3θ)
√
2
√
π
dθ (5.153)
> A(0):=value(%);
A(0) := 0 (5.154)
Generalized series terms
> u[0](r,theta):=eval(R[0](r)*phi[0](theta));u[n](r,theta):=R[n](r)*(A(n)*phi[n](theta)
+B(n)*psi[n](theta));
u
0
(r, θ) := 0
u
n
(r, θ) := r
n
δ(n, 3) sin(nθ) (5.155)
Series solution
> u(r,theta):=u[0](r,theta)+Sum(u[n](r,theta),n=1..infinity);
u(r, θ) :=
∞
n=1
r
n
δ(n, 3) sin(nθ) (5.156)
First few terms of expansion
> u(r,theta):=rˆ3*sin(3*theta);
u(r, θ) := r
3
sin(3θ) (5.157)
> cylinderplot([r,theta,u(r,theta)],r=0..a,theta=−Pi..Pi,axes=framed,orientation=[21,69],
thickness=1);
1
0.5
0
20.5
21
21
20.5
0
0.5
1
1
0
21
x
y
z
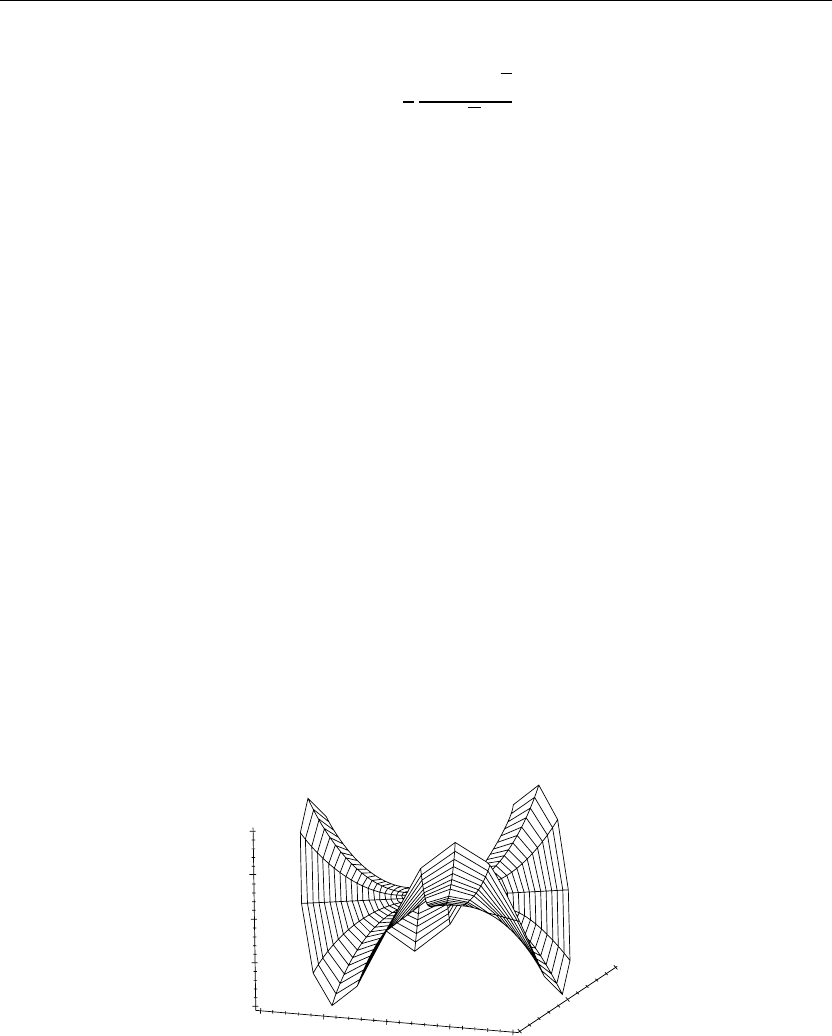
Figure 5.9
The three-dimensional surface shown in Figure 5.9 depicts the steady-state temperature
distribution u(r, θ) over the cylindrical region. Note how the edges of the surface adhere to the

The Laplace Par tial Differential Equation 325
given boundary conditions. The temperature isotherms can be obtained from Maple by clicking
on the figure, choosing the special option “Render the plot using the polygon patch and contour
style” in the graphics bar, and then clicking the “redraw” button.
Chapter Summary
Laplace equation in rectangular coordinates
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
Sturm-Liouville problem with respect to the x variable
d
2
dx
2
X(x)+λX(x) = 0
Homogeneous boundary conditions
κ
1
X(0) +κ
2
X
x
(0) = 0
and
κ
3
X(a)+κ
4
X
x
(a) = 0
Solution in terms of eigenfunctions with respect to the x variable
u(x, y) =
∞
n=0
X
n
(x)
A(n) cosh
λ
n
y
+B(n) sinh
λ
n
y
Sturm-Liouville problem with respect to the y variable
d
2
dy
2
Y(y) +λY(y) = 0
Homogeneous boundary conditions
κ
1
Y(0) +κ
2
Y
y
(0) = 0
and
κ
3
Y(b) +κ
4
Y
y
(b) = 0
Solution in terms of eigenfunctions with respect to the y variable
u(x, y) =
∞
n=0
Y
n
(y)
A(n) cosh
λ
n
x
+B(n) sinh
λ
n
x

326 Chapter 5
Laplace equation in cylindrical coordinates
∂
∂r
u(r, θ) +r
∂
2
∂r
2
u(r, θ)
r
+
∂
2
∂θ
2
u(r, θ)
r
2
= 0
Sturm-Liouville problem with respect to the θ variable
d
2
dθ
2
(θ)+λ(θ) = 0
Homogeneous boundary conditions
κ
1
(0) +κ
2
θ
(0) = 0
and
κ
3
(b)+κ
4
θ
(b) = 0
Solution in terms of eigenfunctions with respect to the θ variable
u(r, θ) =
∞
n=0
n
(θ)
A(n)r
√
λ
n
+B(n)r
−
√
λ
n
Sturm-Liouville problem in terms of the r variable
r
2
d
2
dr
2
R(r)
+r
d
dr
R(r)
+λR(r) = 0
Homogeneous boundary conditions
κ
1
R(1) +κ
2
R
r
(1) = 0
and
κ
3
R(b) +κ
4
R
r
(b) = 0
Solution in terms of eigenfunctions with respect to the r variable
u(r, θ) =
∞
n=0
R
n
(r)
A(n) cosh
λ
n
θ
+B(n) sinh
λ
n
θ
We have considered solutions to the steady-state or time-invariant wave and diffusion equation.
This partial differential equation is called the “Laplace” equation. In electrostatics, this
equation is referred to as the “potential” equation. Solutions to the Laplace equation are said to
be “harmonic.”

The Laplace Par tial Differential Equation 327
Exercises
In the following exercises, we are asked to develop the graphics showing temperature
isotherms and electrostatic equipotential lines. These graphics can be obtained from Maple by
clicking on the figure, choosing the special option “Render the plot using the polygon patch
and contour style” in the graphics bar, and then clicking the “redraw” button.
Exercises in Rectangular Coordinates
5.1. We seek the steady-state temperature distribution in a thin plate over the rectangular
domain D ={(x,y) |0 <x<1, 0 <y<1} whose lateral surface is insulated. The sides
x = 0 and y = 0 are at the fixed temperature of zero, the side x = 1 is insulated, and the
side y = 1 has a given temperature distribution. The boundary conditions are
u(0,y)= 0 and u
x
(1,y)= 0
u(x, 0) = 0 and u(x, 1) = x
1 −
x
2
Develop the graphics for the three-dimensional temperature surface showing the
isotherms.
5.2. We seek the steady-state temperature distribution in a thin plate over the rectangular
domain D ={(x,y) |0 <x<1, 0 <y<1} whose lateral surface is insulated. The sides
y = 0 and y = 1 are at a fixed temperature of zero, the side x = 1 is insulated, and the
side x = 0 has a given temperature distribution. The boundary conditions are
u(0,y)= y(1 −y) and u
x
(1,y)= 0
u(x, 0) = 0 and u(x, 1) = 0
Develop the graphics for the three-dimensional temperature surface showing the
isotherms.
5.3. We seek the electrostatic potential in a charge-free rectangular domain
D ={(x,y) |0 <x<1, 0 <y<1}. The sides x = 0,x= 1, and y = 1 are held at a fixed
potential of zero, and the side y = 0 has a given potential distribution. The boundary
conditions are
u(0,y)= 0 and u(1,y)= 0
u(x, 0) = x(1 −x) and u(x, 1) = 0
Develop the graphics for the three-dimensional equipotential surfaces showing the
equipotential lines.
5.4. We seek the steady-state temperature distribution in a thin plate over the rectangular
domain D ={(x,y) |0 <x<1, 0 <y<1} whose lateral surface is insulated. The sides
