Антошина И.В., Котов Ю.Т. Микропроцессоры и микропроцессорные системы (аналитический обзор)

Подождите немного. Документ загружается.

251

ходных значений, не зависящих от предыдущего состояния се-

ти. Рекуррентные сети являются динамическими, так как в силу

обратных связей в них модифицируются входы нейронов, что при-

водит к изменению состояния сети.

Здесь каждый нейрон передает свой выходной сигнал ос-

тальным нейронам, включая самого себя. Выходными сигналами

сети могут быть все или

некоторые выходные сигналы нейронов

после нескольких тактов функционирования сети. Все входные

сигналы подаются всем нейронам. Элементы слоистых и полно-

связных сетей могут выбираться по-разному. Существует, впро-

чем, стандартный выбор: нейрон с адаптивным неоднородным ли-

нейным сумматором на входе. Для полносвязной сети входной

сумматор нейрона фактически распадается на два: первый

вычис-

ляет линейную функцию от входных сигналов сети, второй линей-

ную функцию от выходных сигналов других нейронов, получен-

ных на предыдущем шаге. Функция активации нейронов (характе-

ристическая функция) это нелинейный преобразователь выходного

сигнала сумматора. Если функция одна для всех нейронов сети, то

сеть называют однородной (гомогенной). Если же характеристиче-

ская функция

зависит еще от одного или нескольких параметров,

значения которых меняются от нейрона к нейрону, то сеть назы-

вают неоднородной (гетерогенной).

Составлять сеть из нейронов стандартного вида не обяза-

тельно. Слоистая или полносвязная архитектуры не налагают су-

щественных ограничений на участвующие в них элементы. Един-

ственное жесткое требование, предъявляемое архитектурой к

эле-

ментам сети, это соответствие размерности вектора входных сиг-

налов элемента (она определяется архитектурой) числу его входов.

Если полносвязная сеть функционирует до получения ответа за-

данное число тактов k, то ее можно представить как частный слу-

чай k-слойной сети, все слои которой одинаковы и каждый из них

соответствует такту функционирования полносвязной сети

Существенное различие между полносвязной и слоистой

сетями становится очевидным, когда число тактов функциониро-

вания заранее не ограничено и слоистая сеть так работать не мо-

жет. Доказаны теоремы о полноте: для любой непрерывной функ-

ции нескольких переменных можно построить нейронную сеть,

252

которая вычисляет эту функцию с любой заданной точностью.

Так что нейронные сети в каком-то смысле могут все.

Способность к обучению является фундаментальным свой-

ством мозга. В контексте ИНС процесс обучения может рассмат-

риваться как настройка архитектуры сети и весов связей для эф-

фективного выполнения специальной задачи. Обычно нейронная

сеть должна

настроить веса связей по имеющейся обучающей вы-

борке. Функционирование сети улучшается по мере итеративной

настройки весовых коэффициентов. Свойство сети обучаться на

примерах делает их более привлекательными по сравнению с сис-

темами, которые следуют определенной системе правил функцио-

нирования, сформулированной экспертами.

Для конструирования процесса обучения, прежде всего, не-

обходимо иметь модель

внешней среды, в которой функционирует

нейронная сеть - знать доступную для сети информацию. Эта мо-

дель определяет парадигму обучения. Во-вторых, необходимо по-

нять, как модифицировать весовые параметры сети - какие прави-

ла обучения управляют процессом настройки. Алгоритм обучения

означает процедуру, в которой используются правила обучения

для настройки весов.

Существуют три парадигмы обучения

: "с учителем", "без

учителя" (самообучение) и смешанная. В первом случае нейронная

сеть располагает правильными ответами (выходами сети) на каж-

дый входной пример. Веса настраиваются так, чтобы сеть произ-

водила ответы как можно более близкие к известным правильным

ответам. Усиленный вариант обучения с учителем предполагает,

что известна только критическая оценка правильности

выхода

нейронной сети, но не сами правильные значения выхода. Обуче-

ние без учителя не требует знания правильных ответов на каждый

пример обучающей выборки. В этом случае раскрывается внут-

ренняя структура данных или корреляции между образцами в сис-

теме данных, что позволяет распределить образцы по категориям.

При смешанном обучении часть весов определяется

посредством

обучения с учителем, в то время как остальная получается с по-

мощью самообучения.

Теория обучения рассматривает три фундаментальных

свойства, связанных с обучением по примерам: емкость, слож-

253

ность образцов и вычислительная сложность. Под емкостью

понимается, сколько образцов может запомнить сеть, и какие

функции и границы принятия решений могут быть на ней сформи-

рованы. Сложность образцов определяет число обучающих при-

меров, необходимых для достижения способности сети к обобще-

нию. Слишком малое число примеров может вызвать "переобу-

ченность" сети, когда

она хорошо функционирует на примерах

обучающей выборки, но плохо - на тестовых примерах, подчинен-

ных тому же статистическому распределению.

Известны 4 основных типа правил обучения: коррекция по

ошибке, машина Больцмана, правило Хебба и обучение методом

соревнования.

- правило коррекции по ошибке. При обучении с учителем

для каждого входного примера задан желаемый выход d. Реальный

выход сети y может не совпадать с желаемым. Принцип коррекции

по ошибке при обучении состоит в использовании сигнала (d-y)

для модификации весов, обеспечивающей постепенное уменьше-

ние ошибки. Обучение имеет место только в случае, когда перцеп-

трон ошибается. Известны различные модификации этого алго-

ритма обучения.

- обучение Больцмана представляет собой стохастическое

правило обучения, которое

следует из информационных теорети-

ческих и термодинамических принципов. Целью обучения Больц-

мана является такая настройка весовых коэффициентов, при кото-

рой состояния видимых нейронов удовлетворяют желаемому рас-

пределению вероятностей. Обучение Больцмана может рассматри-

ваться как специальный случай коррекции по ошибке, в котором

под ошибкой понимается расхождение корреляций состояний в

двух режимах .

- правило Хебба: если нейроны с обеих сторон синапса ак-

тивизируются одновременно и регулярно, то сила синаптической

связи возрастает. Важной особенностью этого правила является то,

что изменение синаптического веса зависит только от активности

нейронов, которые связаны данным синапсом. Это существенно

упрощает цепи обучения в реализации VLSI.

- обучение методом соревнования. В отличие от

обучения

Хебба, в котором множество выходных нейронов могут возбуж-

254

даться одновременно, при соревновательном обучении выход-

ные нейроны соревнуются между собой за активизацию. Это явле-

ние известно как правило "победитель берет все". Подобное обу-

чение имеет место в биологических нейронных сетях. Обучение

посредством соревнования позволяет кластеризовать входные

данные: подобные примеры группируются сетью в соответствии с

корреляциями и представляются одним элементом. При

обучении

модифицируются только веса "победившего" нейрона. Эффект

этого правила достигается за счет такого изменения сохраненного

в сети образца (вектора весов связей победившего нейрона), при

котором он становится чуть ближе ко входному примеру.

Одной из особенностей нейросетевых методов обработки

информации является высокая параллельность вычислений и, сле-

довательно, целесообразность использования специальных средств

аппаратной поддержки. В значительной мере успех в решении

рассмотренных задач обусловлен использованием оригинальных

ускорительных плат. Такие платы работают параллельно с процес-

сором обыкновенного ПК и несут на себе основную вычислитель-

ную нагрузку, превращая основной процессор компьютера в уст-

ройство управления и обслуживания мощных вычислительных

средств, расположенных на ускорительной плате.

Например в

НТЦ "Модуль" разработаны многопроцессор-

ные ускорительные платы МЦ5.001 и МЦ5.002. Первая из них

имеет в своем составе 4 микропроцессора TMS320C40 с тактовой

частотой 50 МГц и пиковой производительностью 275 MIPS. Каж-

дый процессор имеет свою локальную статическую память объе-

мом 1 Мбайт. К 2 процессорам дополнительно подключены 2 бло-

ка динамической памяти объемом 16 Мбайт каждый. К одному из

процессоров подключена также статическая память объемом 1

Мбайт, используемая для обмена данными с ПК. Процессоры со-

единены друг с другом специальными высокоскоростными кана-

лами с пропускной способностью 20 Мбайт/с каждый. Наращива-

ние и комплексирование плат осуществляется на материнской пла-

те ПК с помощью шины ISA.

Ускорительная плата МЦ5.002 содержит 6 процессоров

TMS320C40 и выполнена

в конструктиве VME, что позволяет ис-

255

пользовать ее в бортовых системах, расположенных на лета-

тельном аппарате.

Нейропроцессор обычно состоит из двух основных блоков:

скалярного, выполняющего роль универсального вычислительного

устройства, и векторного, ориентированного на выполнение век-

торно-матричных операций. Скалярное устройство обеспечивает

интерфейсы с памятью и коммуникационными портами, позво-

ляющими объединять процессоры в вычислительные сети различ-

ной конфигурации

. Основное назначение скалярного устройства -

подготовка данных для векторной части процессора. Для этого

существует несколько режимов адресации, интерфейс с памятью,

наборы арифметических и логических операций, возможность ра-

боты с регистровыми парами.

Центральным звеном нейропроцессора является целочис-

ленное векторное устройство, обладающее возможностями обра-

ботки данных различной разрядности. Оно оперирует n-

разрядными словами. Таким

образом, процессор рассчитан на вы-

сокопроизводительную обработку больших массивов целочислен-

ных данных. К примеру отечественный нейропроцессор, разрабо-

танный в НТЦ "Модуль". Скалярное устройство обеспечивает ин-

терфейсы с памятью и 2 коммуникационными портами. Скалярное

устройство имеет адресных регистров и такое же количество реги-

стров общего назначения разрядностью 32 бита каждый.

Центральным звеном нейропроцессора является

целочис-

ленное векторное устройство, обладающее возможностями обра-

ботки данных различной разрядности. Оно оперирует 64-

разрядными словами, которые могут быть разбиты на целочислен-

ные составляющие практически произвольной разрядности в пре-

делах от 1 до 64 бит. На каждую инструкцию векторного процес-

сора затрачивается от 1 до 32 тактов. При этом одновременно об-

рабатывается до 32 64-разрядных слов.

Для организации непре-

рывной подачи данных в операционное устройство (ОУ) векторно-

го процессора используются внутренние блоки памяти, называе-

мые векторными регистрами. Они выполняют роль буфера опе-

рандов, буфера для хранения матрицы весов, очереди результатов.

При выполнении команды в операционном устройстве операнды

по очереди извлекаются из внутреннего буфера и подаются на

256

один из входов ОУ. Внутри ОУ производятся вычисления, а их

результат заносится в буфер результатов. Векторные инструкции,

хотя и занимают несколько тактов процессорного времени, могут

выполняться параллельно с инструкциями скалярного процессора.

Таким образом, процессор рассчитан на высокопроизводительную

обработку больших массивов целочисленных данных.

Нейропроцессор выполнен по технологии 0,5 мкм. Его так-

товая частота

33 МГц. На специальных векторно-матричных опе-

рациях он дает увеличение производительности в десятки раз по

сравнению с процессором TMS320C40. Благодаря наличию ком-

муникационных портов с интерфейсом, идентичным портам

TMS320C40, нейропроцессор может быть интегрирован в гетеро-

генную многопроцессорную систему.

Для нейропроцессора разработан полный пакет системного

программного обеспечения, включая символьный отладчик, и ряд

прикладных

библиотек, в частности библиотеку векторно-

матричных вычислений.

Специфика рассматриваемых вычислительных средств и

решаемых задач обуславливает новые требования к технике про-

граммирования. Программисту приходится оперировать другими

категориями, по-другому строить логику программы, решать зада-

чи, которые не могли возникнуть при традиционном программи-

ровании. Перед ним стоит задача - максимально эффективно ис-

пользовать

ресурсы вычислительной системы, правильно распре-

делить нагрузку между процессорами, задействовать их специ-

фичные возможности.

Здесь на первый план выходят методы параллельной обра-

ботки данных. Причем слова "параллельная обработка" можно по-

нимать как обработку на параллельно работающих процессорах,

так и одновременную обработку нескольких элементов данных на

одном процессоре. Современный процессор позволяет выполнять

несколько инструкций за один такт, что заставляет программиста

продумывать как способы организации самих вычислений, так и

способы подготовки данных, для того чтобы параллельно выпол-

няемые процессы не блокировали друг друга.

Трудности, возникающие при программировании много-

процессорных систем, хорошо известны: синхронизация парал-

257

лельных процессов, механизмы обмена данными, проблемы

"критических участков", когда несколько процессов задействуют

одни и те же ресурсы. Еще одной важной особенностью современ-

ных процессоров является высокая разрядность операндов, напри-

мер 64 бита, что позволяет размещать в них по несколько малораз-

рядных элементов данных и обрабатывать их параллельно. Приме-

ром эффективного использования

отмеченной особенности совре-

менных процессоров является технология MMX, где 64-разрядный

регистр разбивается на 8 независимых байтов или на 4 16-битных

слова, которые обрабатываются параллельно. Независимость эле-

ментов состоит в том, что при смещениях или вычитании не про-

исходит заимствования битов у соседних элементов.

По сравнению с обычными компьютерами, нейрокомпью-

теры обладают рядом преимуществ. Во

первых — высокое быст-

родействие, связанное с тем, что алгоритмы нейроинформатики

обладают высокой степенью параллельности. Во вторых — нейро-

системы делаются очень устойчивыми к помехам и разрушениям.

В третьих — устойчивые и надежные нейросистемы могут созда-

ваться из ненадежных элементов, имеющих значительный разброс

параметров.

Несмотря на перечисленные выше преимущества, эти уст-

ройства имеют ряд

недостатков:

1. Они создаются специально для решения конкретных за-

дач, связанных с нелинейной логикой и теорией самоорганизации.

Решение таких задач на обычных компьютерах возможно только

численными методами.

2. В силу своей уникальности эти устройства достаточно

дорогостоящи.

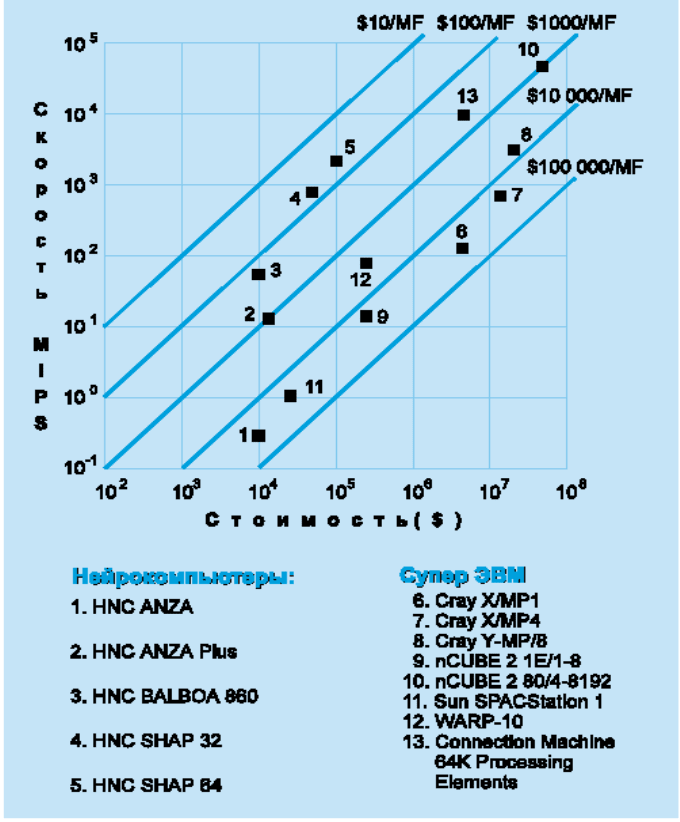
Иллюстрацией преимуществ нейросистем по сравнению с

другими их типами может быть диаграмма, представленная на

рис.70.

Большинство современных нейросистем представляют со-

бой просто персональный компьютер или рабочую станцию, в со-

став которых входит дополнительная нейроплата. К их числу от-

носятся, например, компьютеры серии FMR фирмы Fujitsu. Такие

системы имеют бесспорное право на существование, поскольку их

возможностей вполне достаточно для разработки новых алгорит-

258

мов и решения большого числа прикладных задач методами

нейроматематики.

Рис. 70

Однако наибольший интерес представляют специализиро-

ванные нейрокомпьютеры, непосредственно реализующие прин-

ципы НС. Типичными представителями таких систем являются

259

компьютеры семейства Mark фирмы TRW (первая реализация

перцептрона, разработанная Розенблатом, называлась Mark I).

Модель Mark III фирмы TRW представляют собой рабочую

станцию, содержащую до 15 процессоров семейства Motorola

68000 с математическими сопроцессорами. Все процессоры объе-

динены шиной VME. Архитектура системы, поддерживающая до

65 000 виртуальных процессорных элементов с более чем 1 млн.

настраиваемых соединений, позволяет обрабатывать до 450 тыс.

межсоединений/с.

Mark IV - это однопроцессорный суперкомпьютер

с конвей-

ерной архитектурой. Он поддерживает до 236 тыс. виртуальных

процессорных элементов, что позволяет обрабатывать до 5 млн.

межсоединений/с.

Компьютеры семейства Mark имеют общую программную

оболочку ANSE (Artificial Neural System Environment), обеспечи-

вающую программную совместимость моделей.

Помимо указанных моделей фирмы TRW предлагает также

пакет Mark II - программный эмулятор НС.

Другой интересной моделью является нейрокомпьютер

NETSIM, созданный фирмой Texas Instruments на базе разработок

Кембриджского

университета. Его топология представляет собой

трехмерную решетку стандартных вычислительных узлов на базе

процессоров 80188. Компьютер NETSIM используется для моде-

лирования таких моделей НС, как сеть Хопфилда - Кохонена и НС

с обратным распространением. Его производительность достигает

450 млн. межсоединений/с.

Фирма Computer Recognitiion Systems (CRS) продает серию

нейрокомпьютеров WIZARD/CRS 1000, предназначенных для об-

работки видеоизображений. Размер входной изображения 512 x

512 пиксел. Модель

CRS 1000 уже нашла применение в промыш-

ленных системах автоматического контроля.

8.6.11. Масштабируемая архитектура

Ярким примером масштабируемой архитектуры является

система Cray T3E, которая использует микропроцессоры DEC

21164 (DEC Alpha EV5), RISK-процессоры с пиковой производи-

260

тельностью 600 Мфлоп и 21164А для машин Cray T3E-900 и

Cray T3E-1200. Каждый

процессорный элемент (ПЭ) Cray

T3E имеет свою собственную

DRAM-память объёмом от 64

Мбайт до 2 Гбайт. В отличие от

системы CRAY T3D, в которой

исполняемая задача запрашивает

фиксированное количество

процессоров на все время

выполнения, в CRAY T3E

неиспользуемые процессоры могут

использоваться другими задачами.

Модели T3E, T3E-900, T3E-1200,

Т3Е-1350.

Каждый узел в

системе

содержит один процессорный эле-

мент (ПЭ), включающий процессор, память и средство коммута-

ции, которое осуществляет связь между ПЭ. Система конфигури-

руется до 2048 процессоров. Пиковая производительность состав-

ляет 2,4 Тфлоп.

Разделяемая, высокопроизводительная, глобально адресуе-

мая подсистема памяти делает возможным обращение к локальной

памяти каждого ПЭ в Cray T3E. Процессорные элементы в системе

Cray T3E связаны

в трехмерный тор двунаправленной высокоско-

ростной сетью с малым временем задержки, которая в шесть раз

превосходит по скорости аналогичную сеть в Cray T3D. Также до-

бавлена адаптивная маршрутизация, при которой возможен обход

участков с высокой эффективностью передачи.

Cray T3E выполняют операции ввода/вывода через много-

численные порты на один или более каналы GigaRing. Каналы

ввода/

вывода интегрированы в 3-х мерную межузловую сеть и

пропорциональны размеру системы. При этом при добавлении ПЭ

пропускная способность каналов ввода/вывода увеличивается и

масштабируемые приложения могут выполнятся на системах с

большим числом процессоров также эффективно, как на системах

с меньшим числом процессоров.