Angermann L. (ed.). Numerical Simulations - Applications, Examples and Theory
Подождите немного. Документ загружается.

Numerical Simulation of Elastic-Plastic Non-Conforming Contact
271
Plastic strains induce residual stresses, namely elastic stresses that would persist after elastic
unloading. These stresses superimpose the ones induced by contact pressure. The resulting
state generates further plastic strain if stress intensity exceeds yield strength. Consequently,
an accurate estimation of stress field in the elastic-plastic body is essential to plastic strain
increment prediction.
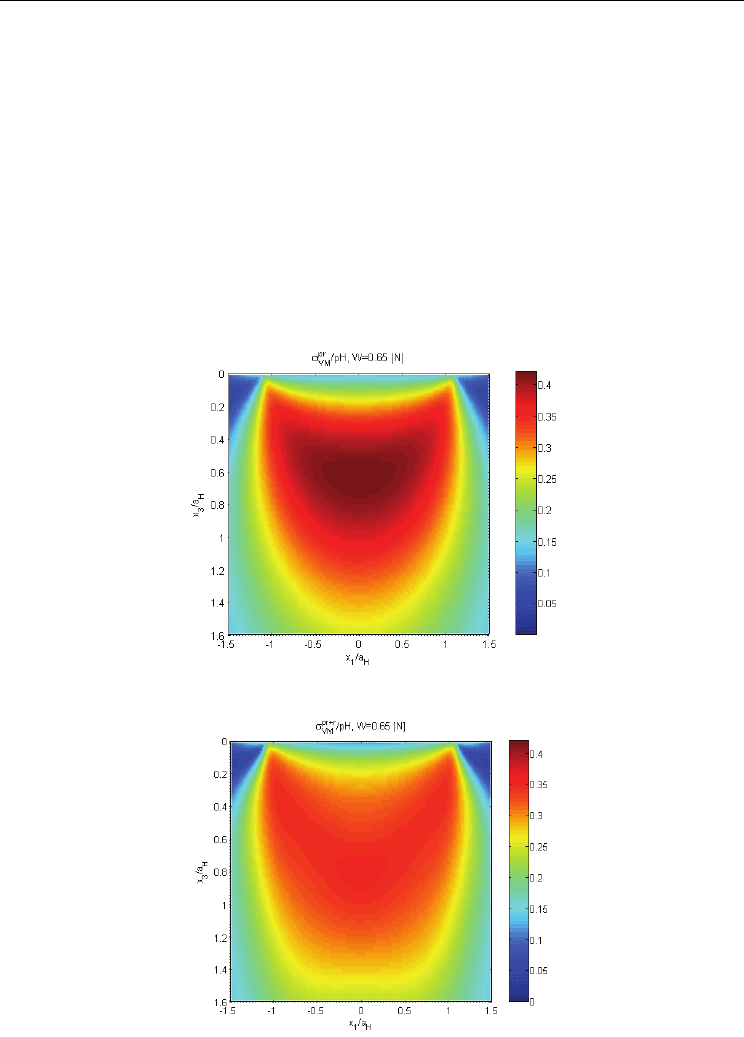
Figures 6 and 7 depict distributions of equivalent von Mises contact stress (stress induced by
contact pressure) and total stress in the elastic-plastic half-space. Residual stress intensity,
Fig. 8, is one order of magnitude smaller than equivalent contact stress. Comparison of
distributions depicted in Figs. 6 and 7, using the same scale, suggests that residual stress
reduces peaks in contact stress intensity, thus making the resulting field more uniform. This
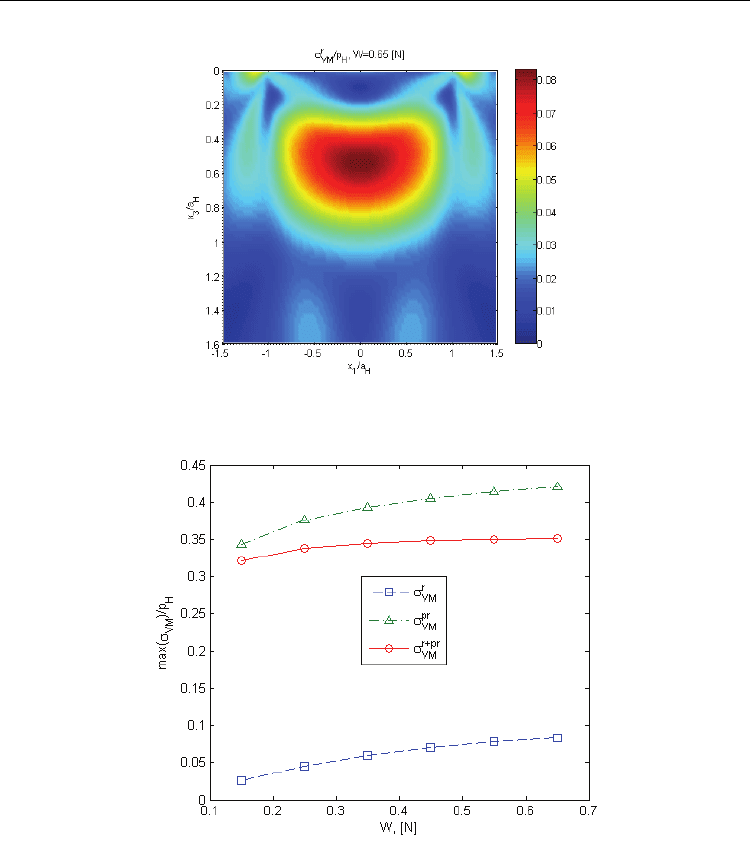
behavior is also suggested by the curves traced in Fig. 9. Maximum intensity of contact
stress increase more rapidly than the maximum of the total field, due to contribution of
residual stress. Consequently, residual stresses, which represent material response to plastic
flow, act to impede further plastic yielding.
Fig. 6. Von Mises stress induced by contact pressure
Fig. 7. Maximum intensities of stress fields versus loading level
Numerical Simulations - Applications, Examples and Theory
272
Fig. 8. Von Mises residual stress
Fig. 9. Total (contact and residual) Von Mises stress in the elastic-plastic body
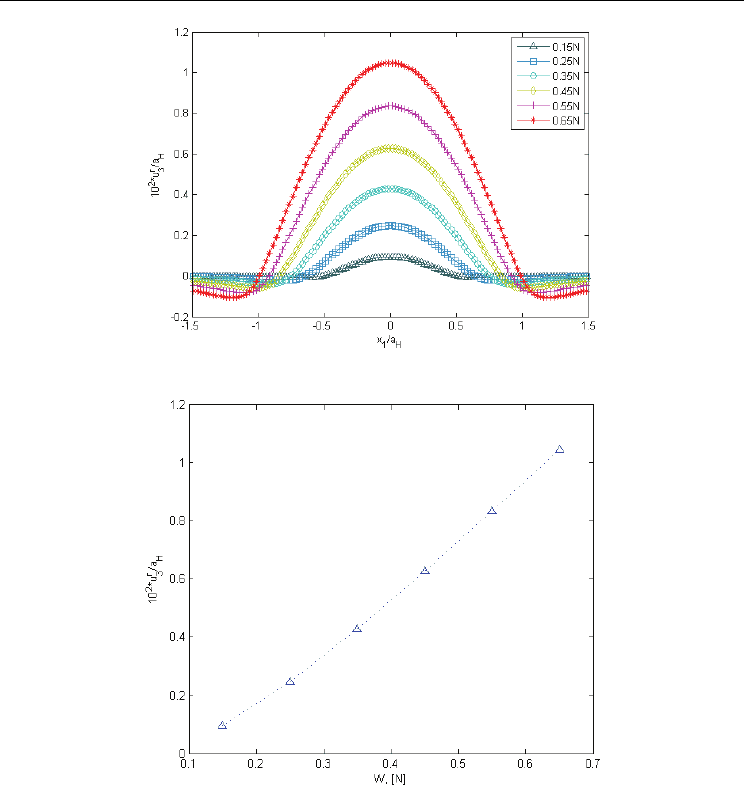
Profiles of residual prints corresponding to the same six loading levels are depicted in Fig.
10. These profiles show that residual displacement increase contact conformity in
investigated non-conforming contact, leading to a more uniform distribution of contact
pressure.
The variation of residual print maximum depth with the loading level is presented in Fig.
11. This curve was also obtained experimentally by El Ghazal, (El Ghazal, 1999), numerically
by Jacq et al., (Jacq et al., 2002), and using FEA by Benchea and Cretu, (Benchea & Cretu,
2008).
Numerical Simulation of Elastic-Plastic Non-Conforming Contact
273
Fig. 10. Residual print profiles in elastic-plastic spherical contact
Fig. 11. Residual print depth versus loading level
6.2 E-EP and EP-EP Contact
Normal residual displacement enters interference equation, by superimposing the
deflections induced by contact pressure. When only one of the contacting bodies, let it be
body (2), is elastic-plastic and the other one, let it be body (1), is elastic, the following
interference equation can be written by superimposing the residual part of
displacement
2
3
()r
u
, related to development of plastic zone in the elastic-plastic body (2), in
elastic contact interference relation, Eq. (7):
12
2
12
33
ω
+
+
=
++−
()
()
()
(, ) (, ) (, ) (, ) .
pr
r
hi j hi i j u i j u i j
(35)
Numerical Simulations - Applications, Examples and Theory
274
On the other hand, when contacting bodies are both elastic-plastic, Eq. (35) encloses residual
displacements of both surfaces, namely
12
3
+()
(, )
r
uij. If the hardening behavior or contacting
bodies is dissimilar, residual displacement should be computed for every body separately.
The model is simplified considerably if the bodies follow the same hardening law and have
the same initial contact geometry, because, due to symmetry of the problem about the
common plane of contact,
12
33
=
() ( )rr
uu. Consequently, Eq. (35) becomes:
12
2
12
33
2
ω
+
+
=
++−
()
()
()
(, ) (, ) (, ) (, ) .
pr
r
hi j hi i j u i j u i j (36)
To validate Eq. (36), the contact between two spheres of radius
0 015= .Rm is simulated
numerically, for two different material behaviors: elastic, and elastic-plastic following
Swift's law, with the following parameters: 945
=
BMPa, 20
=
C , 0 121
=
.n .
The contact is loaded up to a level of 11 179
=
,WN, corresponding to a hertzian pressure
8=
H
p
GPa and to a Hertz contact radius 817
μ
=
H
am.
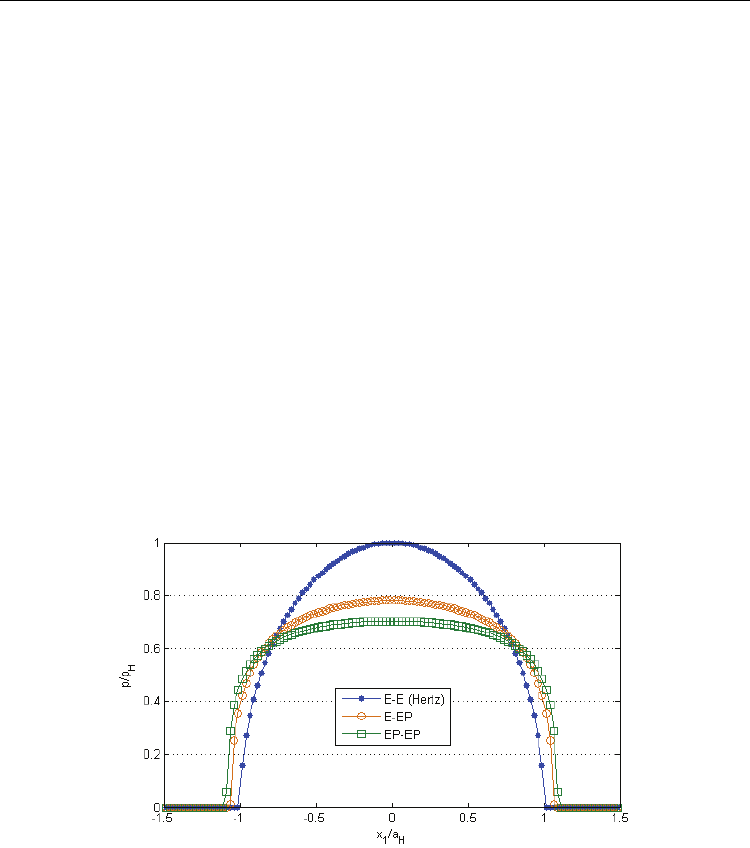
Pressure distributions obtained using Eqs. (35) and (36) respectively, depicted in Fig. 12,
agree well with already published results, (Boucly et al., 2007). As expected, in the EP-EP
contact, pressure appears more flattened compared to the E-EP case, due to a more
pronounced increasing in contact conformity related to doubling of the residual term.
Fig. 12. Pressure profiles for various material behaviors
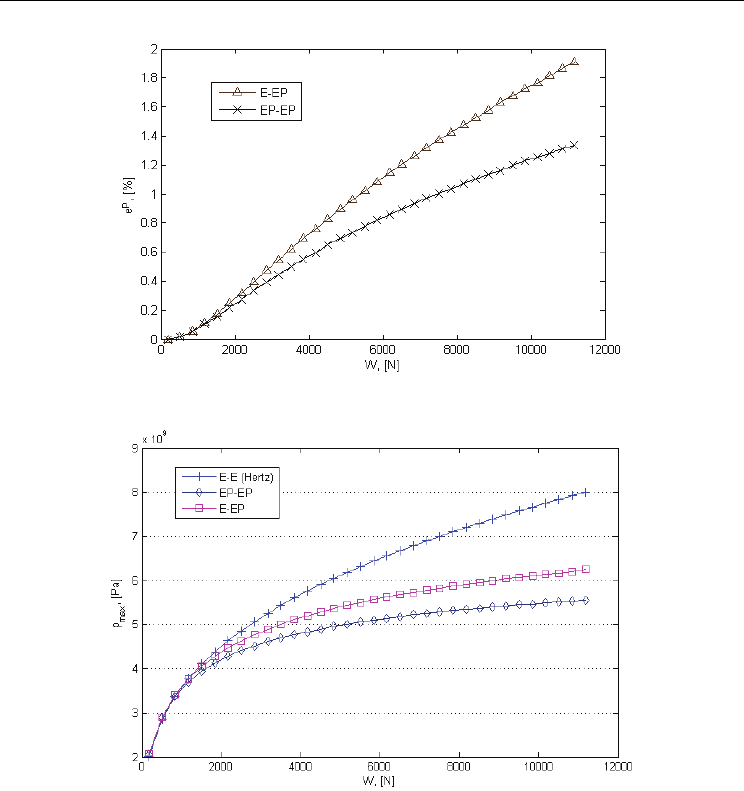
Variations of maximum effective plastic strain with loading level, in the E-EP and in the EP-
EP contact respectively, are depicted in Fig. 13. Intensity of plastic strains in the E-EP contact
is up to 40% higher than the one corresponding to the EP-EP scenario.
Variations of maximum pressure with the loading level in the E-E, the E-EP and the EP-EP
contact, are depicted in Fig. 14. The curves presented in Figs. 13 and 14 also match well the
results of Boucly, Nélias, and Green, (Boucly et al., 2007).
Numerical Simulation of Elastic-Plastic Non-Conforming Contact
275
Fig. 13. Maximum effective accumulated plastic strain versus loading level
Fig. 14. Maximum pressure versus loading level
6.3 R-EPP contact and experimental validation
As Contact Mechanics uses simplifying assumptions in order to circumvent the
mathematical complexity of the arising equations, experimental validation is needed to
verify model viability. An extended program of experimental research was conducted in
the Contact Mechanics Laboratory of the University of Suceava, aiming to assess residual
print parameters in rough elastic-plastic non-conforming contacts. The stand used for the
loading experiments was originally designed by Nestor et al., (Nestor et al., 1996).
Microtopography of deformed surface was scanned with a laser profilometer UBM14.
Contact between a steel ball, assumed as a rigid indenter, and a lead specimen, simulating
the elastic-plastic half-space, was loaded up to an equivalent hertzian pressure
Numerical Simulations - Applications, Examples and Theory
276
094= .
H
p
GPa . The contact was also simulated using the numerical formulation. As lead is
best described as an EPP material, a linear hardening law with a very small slope was
considered in the numerical model. As stated in (Jacq, 2001), the plastic strain increment is
undefined when assuming a purely EPP material behavior.
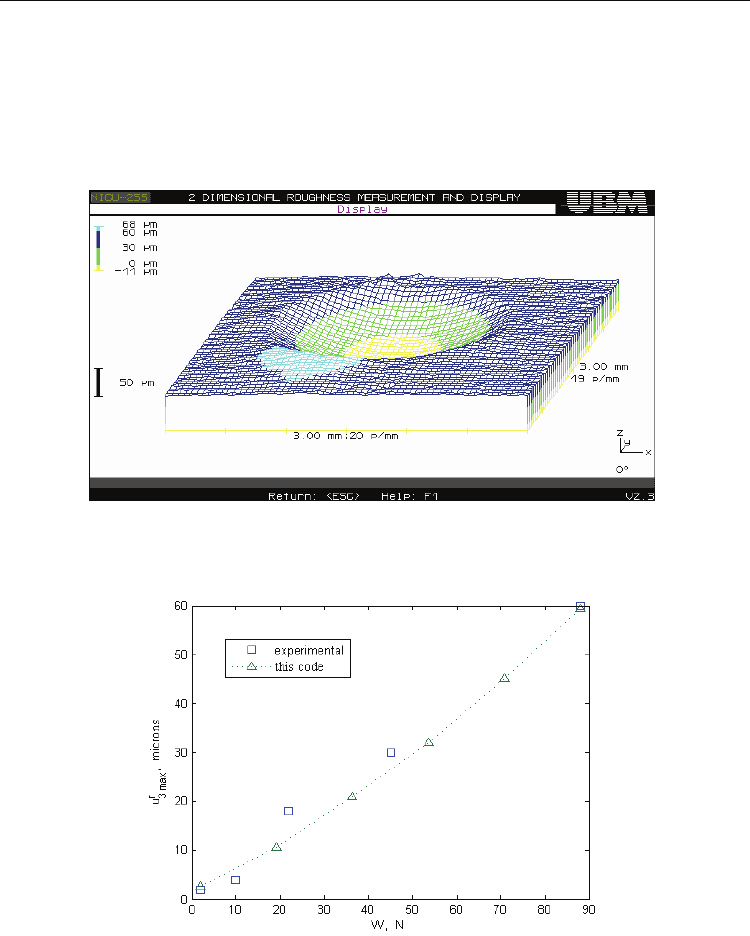
Residual prints at a hertzian pressure of
094. GPa is depicted in Fig. 15.
Fig. 15. Experimental residual print in R-EPP contact,
094= .
H
p
GPa
Fig. 16. Residual print depth versus loading level
Variation of print depth with loading level is presented in Fig. 16. The agreement between
the values predicted numerically and those obtained experimentally is considered
satisfactory, giving the complexity of the phenomena involved.

Numerical Simulation of Elastic-Plastic Non-Conforming Contact
277
6. Conclusions
A numerical approach for simulating the elastic-plastic contact with isotropic hardening,
based on Betti’s reciprocal theorem, is overviewed in this paper. Problem decomposition, as
originally suggested by Mayeur and later by Jacq, is employed to assess pressure and plastic
strain distribution, on three nested iterative levels.
The newly proposed algorithm has two major advantages over other existing methods.
Firstly, the plastic strain increment is determined in a fast convergent Newton-Raphson
procedure which iterates a scalar, namely the effective accumulated plastic strain. The
method, originally suggested by Fotiu and Nemat-Nasser, employs an elastic predictor,
which places the trial state outside yield surface, and a plastic corrector, used to derive the
return path to the yield locus. The algorithm is fast, stable, and accurate even for large
loading increments.
An additional advantage arises from moving residual stress computation, which is very
computationally intensive, to an upper iterative level.
Secondly, the use of three-dimensional spectral methods for solving the intrinsically three-
dimensional inclusion problem improves dramatically the overall algorithm efficiency.
Solution is obtained by problem decomposition, following a method originally suggested by
Chiu. Subproblem of stresses due to eigenstrains in infinite space is solved using influence
coefficients also derived by Chiu. Traction-free surface condition is imposed with the aid of
Boussinesq fundamental solutions, in a simplified formulation, well adapted to elastic-
plastic contact modeling.
With the newly advanced three-dimensional convolution and convolution-correlation
hybrid algorithm, based on the DCFFT technique, the computational effort is reduced
dramatically, allowing for finer grids in problem discretization.
The newly proposed algorithm was used to simulate, with a high resolution of 120 120 80××
elementary cells, the spherical contact between bodies with various behaviors: R-EP, E-EP,
EP-EP and R-EPP.
Elastic-plastic pressure appears flattened compared to the elastic case, due to changes in
hardening state of the EP material, and in contact conformity due to superposition of
residual displacement in interference equation.
Plastic zone, initially occupying a hemispherical region located at hertzian depths, advances
toward half-space boundary with increased loading, enveloping an elastic core. This
development is consistent with existing models for the elastic-plastic process, marking the
passing from elastic-plastic range to fully plastic.
Residual stress intensity is one order of magnitude smaller than equivalent stresses induced
by contact pressure. They contribute to total elastic field by decreasing the peaks in contact
stress intensity, thus impeding further plastic flow.
A modified interference equation is used for solving the EP-EP contact with similar
hardening behavior and symmetry about the common plane of contact.
Furthermore, residual displacement predicted numerically for the R-EPP contact match well
print depths obtained experimentally in indentation of a lead specimen, assumed as an EPP
half-space, with a steel ball assumed as a rigid indenter.

Numerical Simulations - Applications, Examples and Theory
278
7. Acknowledgement
This paper was supported by the project “Progress and development through post-doctoral
research and innovation in engineering and applied sciences – PRiDE - Contract no.
POSDRU/89/1.5/S/57083”, project co-funded from European Social Fund through
Sectorial Operational Program Human Resources 2007-2013.
Grant CNCSIS 757/2007-2008, entitled “Research upon the Effects of Initial Stresses in
Dental Biocontacts” provided partial support for this work.
8. References
Antaluca, E. (2005). Contribution a l'étude des contacts élasto-plastiques - effet d'un
chargement normal et tangentiel. Ph.D. Thesis, INSA Lyon, France.
Benchea, M. & Cretu, S. (2008). An Improved Incremental Model to Analyse Elastic - Plastic
Concentrated Contacts – The Finite Element Analysis and Validation.
Acta
Tribologica
, Vol. 16, ISSN 1220-8434.
Boucly, V., Nélias, D., & Green, I. (2007). Modeling of the Rolling and Sliding Contact
Between Two Asperities.
J. Tribol. (Trans. ASME), Vol. 129, pp. 235 - 245.
Boussinesq, J. (1969).
Application des potentiels á l'etude de l'equilibre et du mouvement des solides
élastiques
. Reed. A. Blanchard, Paris.
Chen, W. W., Wang, Q. J., Wang, F., Keer, L. M., & Cao, J. (2008). Three-Dimensional
Repeated Elasto-Plastic Point Contacts, Rolling, and Sliding.
J. Tribol. (Trans.
ASME)
, Vol. 75, pp. 021021-1 - 021021-12.
Chiu, Y. P. (1977). On the Stress Field Due to Initial Strains in a Cuboid Surrounded by an
Infinite Elastic Space.
J. Appl. Mech. (Trans. ASME), Vol. 44, p. 587-590.
Chiu, Y. P. (1978). On the Stress Field and Surface Deformation in a Half Space with
Cuboidal Zone in Which Initial Strains Are Uniform.
J. Appl. Mech. (Trans. ASME),
Vol. 45, p. 302-306.
El Ghazal, H. (1999). Etude des proprietes microstructurales et mecaniques des aciers
16NiCrMo13 cemente et 32CrMoV13 nitrure - Application a la prevision de leur
limite d’endurance en fatigue de roulement. Ph.D. Thesis, INSA Lyon, France.
Fotiu, P. A., & Nemat-Nasser, S. (1996). A Universal Integration Algorithm for Rate-
Dependant Elastoplasticity.
Comput. Struct., Vol. 59, pp. 1173–1184.
Jacq, C. (2001). Limite d'endurance et durée de vie en fatigue de roulement du 32CrMoV13
nitruré en présence d'indentations. Ph.D. Thesis, INSA Lyon, France.
Jacq, C., Nélias, D., Lormand, G., & Girodin, D. (2002). Development of a Three-Dimensional
Semi-Analytical Elastic-Plastic Contact Code.
J. Tribol. (Trans. ASME), Vol. 124, pp.
653–667.
Jin, X., Keer, L. M., and Wang, Q. (2008). Note on the FFT Based Computational Code and Its
Application.
Proceedings of the STLE/ASME International Joint Tribology Conference
IJTC2008
, October 20-22, 2008, Miami, Florida, USA.
Kalker, J. J., van Randen, Y. A.. (1972). A Minimum Principle for Frictionless Elastic Contact
with Application to Non-Hertzian Half-Space Contact Problems.
J. Eng. Math., Vol.
6(2), pp. 193-206.

Numerical Simulation of Elastic-Plastic Non-Conforming Contact
279
Liu, S. B., and Wang, Q. (2002). Studying Contact Stress Fields Caused by Surface Tractions
With a Discrete Convolution and Fast Fourier Transform Algorithm.
J. Tribol.
(Trans. ASME)
, Vol. 124, pp. 36–45.
Liu, S. B., Wang, Q., & Liu, G. (2000). A Versatile Method of Discrete Convolution and FFT
(DC-FFT) for Contact Analyses.
Wear, Vol. 243 (1–2), pp. 101–111.
Liu, S. Wang, Q. (2005). Elastic Fields due to Eigenstrains in a Half-Space.
J. Appl. Mech.
(Trans. ASME)
, Vol. 72, p. 871-878.
Mayeur, C. (1995). Modélisation du contact rugueux élastoplastique. Ph.D. Thesis, INSA
Lyon, France.
Mindlin, R. D., & Cheng, D. H. (1950). Thermoelastic Stress in the Semi-Infinite Solid.
J. Appl.
Phys.
, Vol. 21, p. 931-933.
Mura, T. (1968).
The Continuum Theory of Dislocation. Advances in Material Research, Ed.
Herman, H., Vol. 3, Interscience Publisher.
Mura, T. (1988). Inclusion Problem.
ASME Applied Mechanics Review, Vol. 41, pp. 15-20.
Nélias, D., Boucly, V., & Brunet, M. (2006). Elastic-Plastic Contact Between Rough Surfaces:
Proposal for a Wear or Running-In Model.
J. Tribol. (Trans. ASME), Vol. 128, pp. 236
- 244.
Nestor, T., Prodan, D., Pătraş-Ciceu, S., Alaci, S., & Pintilie, D. (1996). Stand pentru
determinarea histerezisului static la solicitarea de contact (in Romanian).
Proceedings of VAREHD 8, Suceava.
Polonsky, I. A., & Keer, L. M. (1999). A Numerical Method for Solving Rough Contact
Problems Based on the Multi-Level Multi-Summation and Conjugate Gradient
Techniques.
Wear, Vol. 231(2), pp. 206–219.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., Flannery, B. P. (1992).
Numerical Recipes in C
– The Art of Scientific Computing
– Second Edition. Cambridge University Press.
Shewchuk, J. R. (1994). An Introduction to the Conjugate Gradient Method Without the
Agonizing Pain. School of Computer Science, Carnegie Mellon University.
Spinu, S. (2008). A Refined Numerical Method for Elastic Contact Problem with a Tilting
Torque on the Contact Area.
Acta Tribologica, Vol. 16, ISSN 1220-8434.
Spinu, S. (2009). Contributions to the Solution of the Elastic-Plastic Normal Contact Problem
(in Romanian), Ph.D. Thesis, University of Suceava, Romania.
Spinu, S., Diaconescu, E. (2008). Numerical Simulation of Elastic Conforming Contacts
under Eccentric Loading.
Proceedings of the STLE/ASME International Joint Tribology
Conference IJTC2008
, Miami, Florida, USA.
Spinu, S., Diaconescu, E. (2009). A Fast Numerical Method to Predict Elastic Fields Due to
Eigenstrains in an Isotropic Half-Space - Part I. Algorithm Overview.
The Annals of
University “Dunărea de Jos“ of Galati
, Fascicle VIII, 2009 (XV), ISSN 1221-4590, Issue
2, Tribology, pp. 191-196.
Spinu, S., Gradinaru, D. & Marchitan, M. (2007). Improvement of Pressure Distribution in
Elastic Non-Hertzian Contacts – Numerical Simulations.
Acta Tribologica, Vol. 15,
ISSN 1220-8434.
Wang, F., & Keer, L. M. (2005). Numerical Simulation for Three Dimensional Elastic-Plastic
Contact With Hardening Behavior.
J. Tribol. (Trans. ASME), 127, pp. 494–502.

Numerical Simulations - Applications, Examples and Theory
280
Zhou, K., Chen, W. W., Keer, L. M., & Wang, Q. J. (2009). A Fast Method for Solving Three-
Dimensional Arbitrarily Shaped Inclusions in a Half-Space.
Comput. Methods Appl.
Mech. Engrg.
, Vol. 198, p. 885-892.
