Андрейчиков А.В., Андрейчикова О.Н. Анализ, синтез, планирование решений в экономике

Подождите немного. Документ загружается.

Рассмотренная модификация МАИ может эффективно применяться при решении широкого класса

социально-экономических и управленческих задач.

Оценка однородности иерархии

После решения задачи иерархического синтеза оценивается однородность всей иерархии с помощью

суммирования показателей однородности всех уровней, приведенных путем "взвешивания" к первому

иерархическому уровню, где находится корневая вершина. Число шагов алгоритма по вычислению

однородности определяется конкретной иерархией.

Рассмотрим принципы вычисления индекса ИО

и отношения ОО

однородности иерархии.

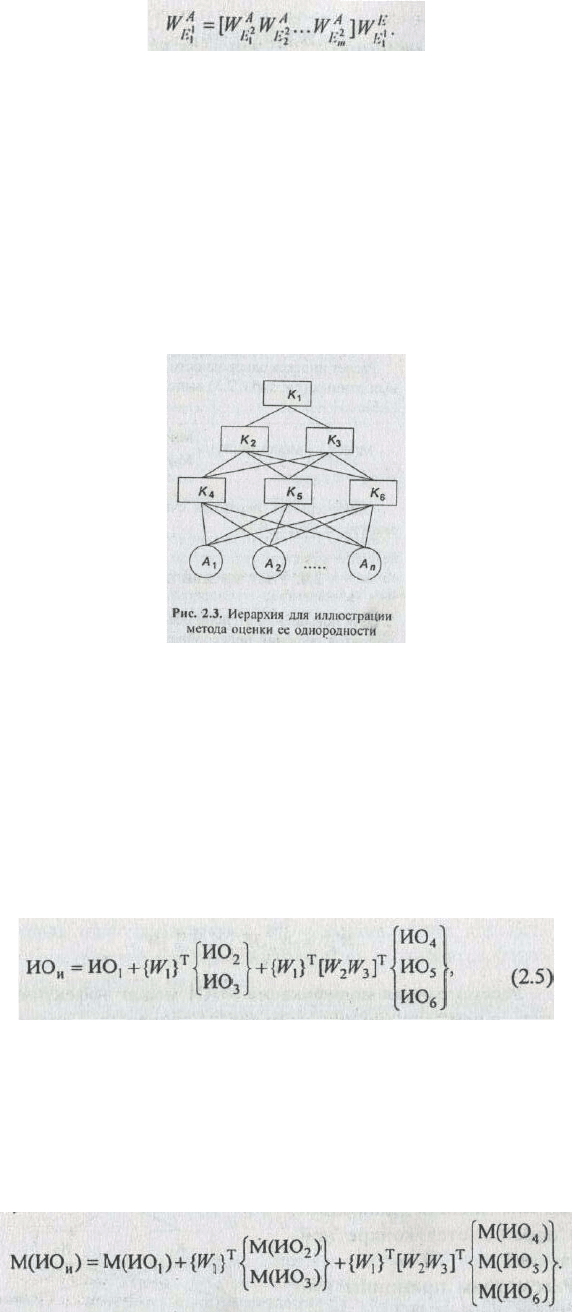
Пусть задана иерархия критериев и альтернатив (рис. 2.3.) и для каждого уровня определен индекс

однородности и векторы приоритетов критериев следующим образом:

ИО

— индекс однородности для 1-го уровня;

{ИО

, ИО

} — индексы однородности для 2-го уровня;

{ИО

, ИО

} — индексы однородности для 3-го уровня;

} — вектор приоритетов критериев К

и К

относительно критерия К

;

},{W

} — векторы приоритетов критериев К

, К

относительно критериев К

и К

второго

уровня.

В этом случае индекс однородности рассматриваемой иерархии можно определить по формуле

где Т — знак транспонирования.

Определение отношения однородности ОО

для всей иерархии осуществляется по формуле

ОО

= ИО

/ М(ИО

где М(ИО

) — индекс однородности иерархии при случайном заполнении матриц попарных

сравнений.

Расчет индекса однородности М(ИО

) с учетом экспериментальных данных (см. табл. 2.3)

выполняется по формуле, аналогичной (2.5):

Однородность иерархии считается удовлетворительной при значениях ОО

≤ 0,10.

2.4. Учет мнений нескольких экспертов

Для повышения степени объективности и качества процедуры принятия решений целесообразно

учитывать мнения нескольких экспертов. С этой целью проводится групповая экспертиза, причем

множество экспертов может быть подразделено на несколько подмножеств в зависимости от области

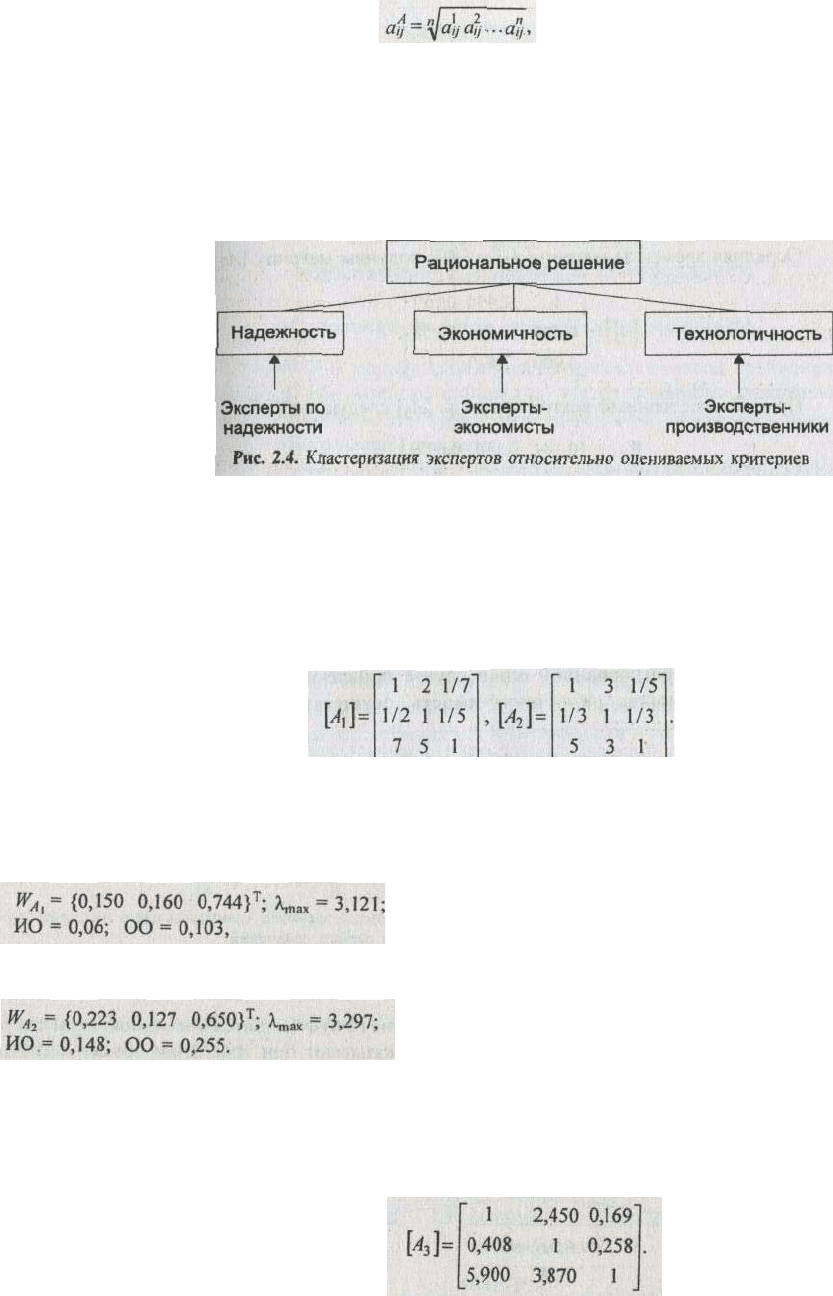
экспертизы [З], определяемой характером критериев, используемых в иерархии. Оценка весомости

критериев и альтернатив с учетом данного подхода предполагает привлечение специалистов-

управленцев, маркетологов, производственников, специалистов-теоретиков и т. п. (рис. 2.4).

Для агрегирования мнений экспертов принимается среднегеометрическое, вычисляемое по

следующему соотношению:

(2.6)

где a

— агрегированная оценка элемента, принадлежащего i-й строке и j-му столбцу матрицы

парных сравнений;

п — число матриц парных сравнений, каждая из которых составлена одним экспертом.

Логичность критерия (2.6) становится очевидной, если два равноценных эксперта указывают при

сравнении объектов соответственно оценки а и 1/а, что при вычислении агрегированной оценки дает

единицу и свидетельствует об эквивалентности сравниваемых объектов.

Осреднение суждений экспертов может быть осуществлено и на уровне собственных векторов

матриц парных сравнений. При этом результаты будут эквивалентны тем, которые получены на уровне

элементов матриц, если однородность составленных матриц достаточна и удовлетворяет условию OO ≤

0,10. Покажем это на следующем примере.

Пусть заданы суждения двух экспертов в виде матриц попарных сравнений [A

] и [A

Для этих матриц собственные векторы W

Аi

, максимальные собственные значения λ

max

и оценки

однородности (ИО; OO) имеют следующий вид:

для матрицы [A

]

Для матрицы [A

Осреднение на уровне элементов собственных векторов дает

= {0,184 0,117 0,699}

Осредняя элементы матриц [A

] [A

], получим матрицу [А

Правый собственный вектор матрицы [А

] следующий:



W= {0,184 0,116 0,699}

Сравнивая два собственных вектора W



W определенных двумя разными способами, можно

убедиться в их совпадении, даже несмотря на то, что однородность суждений эксперта, заполнившего

матрицу [A

], была неудовлетворительной (OO = 0,255 > 0,10).

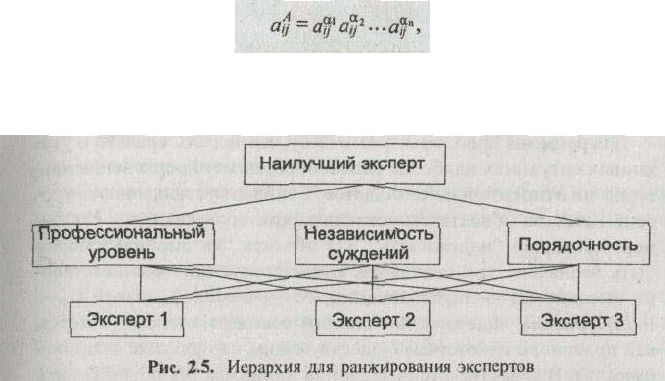
В достаточно ответственных задачах при оправданных затратах на экспертизу осреднение суждений

экспертов проводится с учетом их квалификации ("веса"). Для определения весовых коэффициентов

экспертов целесообразно использовать иерархическую структуру критериев (рис. 2.5).

Расчет агрегированной оценки в случае привлечения п экспертов, имеющих различную значимость,

осуществляется по формуле

где a

— оценка объекта, проведенная k-м экспертом с весовым коэффициентом a

; при этом а

+ а

+...+ а

= 1.

2.5. Методы сравнения объектов относительно стандартов и копированием

Сравнение объектов относительно стандартов

Во второй модификации рассматривается метод сравнения объектов относительно стандартов. Метод

попарного сравнения альтернатив не всегда может быть эффективно применен в некоторых

практических ситуациях:

• эксперту может быть предложено для анализа более девяти альтернатив. В этом случае построение

однородных матриц попарных сравнений становится затруднительным. Это связано с физическими

ограничениями интеллекта человека;

• при добавлении новых альтернатив изменяется порядок ранее прошедших сравнение альтернатив

относительно критериев качества. Нарушение порядка альтернатив нежелательно при решении ряда

прикладных задач, связанных со значительными финансовыми, материальными и социальными

затратами на корректировку последствий принимаемых решений или возможностью возникновения

конфликтной ситуации между экспертами, готовящими и обосновывающими решения, и лицами,

принимающими решения, несущими ответственность за принятые решения и их последствия;

• альтернативы могут поступать эксперту для сравнения не одновременно, а через определенные

промежутки времени. Поэтому в данной ситуации не представляется возможным попарно сравнить

объекты.

Для решения проблемы сравнения и оценки альтернатив в указанных ситуациях наиболее

целесообразен метод сравнения альтернатив

относительно стандартов. Стандарт устанавливает уровень

качества объекта относительно критерия качества. Например, критерию "надежность" для объекта

"автомобиль" может быть назначено три стандарта, характеризующих соответственно высокий (H —

high), средний (М — medium), низкий (L — little) уровень надежности. Каждый стандарт

отождествляется, как правило, с некоторым существующим на практике эталоном качества. В качестве

таких эталонов принимаются объекты, аналогичные сравниваемым альтернативам

. Например, для

видов обеспечения банковских кредитов высокий, средний и низкий стандарты по критерию

"ликвидность" могут быть отождествлены соответственно с драгоценными металлами, ценными бума-

гами и недвижимостью.

В иерархической структуре стандарты присваиваются элементам, имеющим непосредственную связь

с альтернативами. При этом число стандартов по каждому такому элементу (критерию качества) может

быть различно и определяется экспертом с учетом конкретной ситуации. По каждому стандарту

экспертом устанавливается относительная степень предпочтения, которая указывает значимость

стандарта для эксперта. Численное значение каждого стандарта определяется их попарным сравнением

по девятибалльной шкале (см. табл. 2.1) путем обработки матрицы

Вектор приоритетов стандартов будет иметь следующий вид:

{Н= 0,625 М= 0,257 L= 0,091}

Из вышеприведенной матрицы следует, что эксперт отдал слабое предпочтение высокому стандарту

(Н) перед средним (М), а также среднему перед низким стандартом (L). В то же время предпочтение

высокого стандарта (Н) перед низким (L) определено как очень сильное (оценка 7 в матрице).

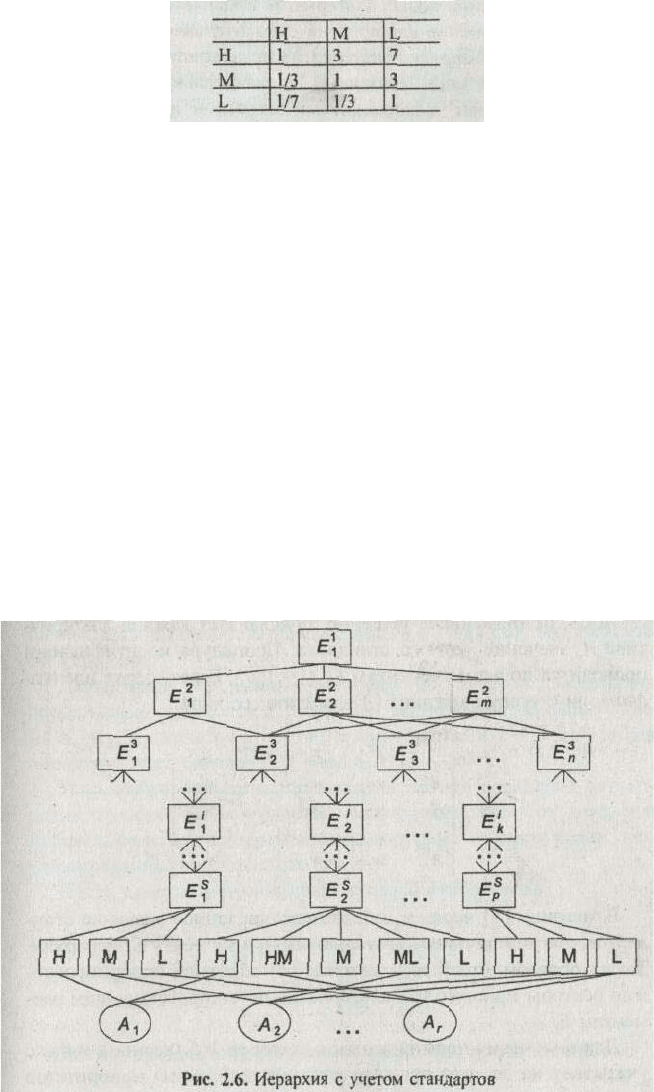
Рассмотрим правила построения иерархии (рис. 2.6), учитывающей стандарты и алгоритм

вычисления векторов приоритетов альтернатив.

Введем следующие обозначения:

С = {С

, C

} — множество стандартов, включающее два подмножества, устанавливающие

соответственно основную { С

} и дополнительную { С

} шкалы. Основная шкала включает градации

{Н, М, L}, где Н, М, L — соответственно высокий, средний и низкий уровень стандартов по

определенному критерию. Дополнительная шкала может включать градации C

= {НН, НМ, ML, LL},

где НН, НМ, ML, LL — соответственно очень высокое; промежуточное между высоким и средним;

промежуточное между средним и низким; очень низкое значение стандартов.

Для конкретного элемента E

, включенного в иерархию из множества С, определяется подмножество

стандартов С

, такое, что С

⊂ С, С

∈ E

. Например, для элементов иерархии (см. рис. 2.6)

и E

определены стандарты Н, М, L, а для элемента Е

— стандарты Н, НМ, М, ML, L. Следует

отметить, что экспертом могут быть назначены различные значения для одних и тех же по

наименованию стандартов, относящихся соответственно к элементам E

и E

Вычисление векторов приоритетов альтернатив относительно элементов иерархии,, учитывающей

стандарты, осуществляется следующим образом.

Для каждого элемента E

иерархии, непосредственно связанного со стандартами, устанавливается

подмножество

⊂ С. Стандарты, входящие в подмножества С

, сформированные относительно E

попарно сравниваются по девятибалльной шкале предпочтений. Относительные предпочтения

стандартов фиксируются в матрицах, обработка которых по итерационному алгоритму, выполняемому

в соответствии с соотношениями (2.2) и (2.3), позволяет определить для них правые собственные

векторы W

∈ E

. В собственном векторе верхний индекс указывает на принадлежность вектора уровню

стандартов в иерархии.

Лицо, принимающее решение, присваивает каждой альтернативе А

значение одного стандарта.

Процедура идентификации проводится по всем элементам E

(j =

p,

). В результате идентификации

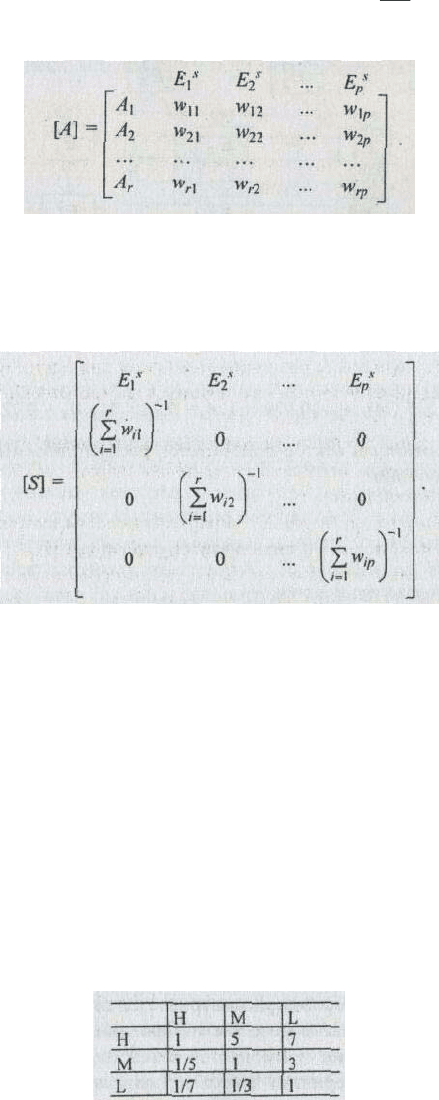
строится матрица [А] следующего вида:

В матрице [А] через w

обозначено численное значение стандартов, соответствующее альтернативе А

и элементу

иерархии. Таким образом, столбцы в матрице [А] образуют ненормированные векторы

приоритетов альтернатив по соответствующим элементам

Для получения нормированных векторов W

(верхний индекс указывает на то, что ранжируются

альтернативы) приоритетов альтернатив матрица [А] умножается на диагональную матрицу [S] вида:

Множество нормированных векторов приоритетов альтернатив относительно всех элементов самого

нижнего уровня иерархии определяется перемножением матриц

]=[A]

[S].

В полученной матрице [ W

] столбцами являются нормированные векторы приоритетов альтернатив

для каждого элемента E

иерархии.

Дальнейшее определение векторов приоритетов альтернатив относительно элементов E

иерархии,

расположенных выше уровня

S, осуществляется в соответствии с шагами 2 и 3 алгоритма

иерархического синтеза (см. разд. 2.3).

Рассмотрим пример использования метода сравнения альтернатив относительно стандартов,

подтверждающий тот факт, что добавление новой альтернативы не нарушает порядок ранее

проранжированных альтернатив.

Пусть имеется матрица предпочтений стандартов:

Вектор приоритетов стандартов имеет следующий вид:

Н = 0,696 М = 0,225 L = 0,079.

Рассмотрим четыре альтернативы

,..., А

которым поставлены в соответствие следующие значения

вектора приоритетов стандартов:

= 0,225 (М), А

= 0,079 (L), А

= 0,225 (М), А

=0,079 (L),

Нормированный вектор приоритетов рассматриваемых альтернатив следующий:

= { 0,370 0,130 0,370 0,130 }

где Т — знак транспонирования;

(4) — нижний индекс, указывающий число ранжируемых альтернатив.

В соответствии с приведенным вектором альтернативы ранжируются в порядке убывания

приоритета: А

, А

Добавим к рассматриваемому множеству альтернатив новую — А

и присвоим ей значение,

соответствующее высокому стандарту — Н. Нормированный вектор приоритетов для пяти альтернатив

имеет следующий вид:

= {0,137 0,061 0,173 0,061 0,534}

В соответствии с этим вектором альтернативы ранжируются в порядке убывания приоритета

следующим образом: А

. Анализ приведенной последовательности показывает, что до-

бавление новой альтернативы А

, не привело к нарушению порядка у ранее проанализированных

альтернатив А

, ..., А

Сравнение объектов методом копирования

В третьей модификации рассматривается определение вектора приоритетов альтернатив методом

копирования.

Метод копирования применяется в тех случаях, когда среди анализируемых альтернатив имеются

такие, которые идентичны по одним или нескольким анализируемым свойствам (критериям качества).

Например, пневматическая виброзащитная система рукавного типа, используемая в рессорном

подвешивании пассажирских автобусов, идентична по качеству виброизоляции с металлическим

механизмом перескока, реализующим квазинулевую жесткость.

Рассмотрим процедуры сравнения и установления приоритета альтернатив, используемые в методе

копирования.

Пусть определено множество альтернатив А = {а

, а

, ..., а

}, каждая из которых отличается от всех

других альтернатив этого множества уровнем качества по рассматриваемому критерию К

и определено

другое множество альтернатив В == {b

, b

, ..., b

}, каждая из которых имеет одинаковые свойства со

всеми другими по ранее определенному критерию К

. Предположим, что множество А имеет хотя бы

один элемент а

, свойство которого по критерию К

идентично свойствам всех альтернатив множества

В. Тогда все альтернативы множества В являются копиями элемента а

по критерию К

. При такой

ситуации эксперт по критерию К

попарно сравнивает только альтернативы множества А. Далее на

основании матрицы попарных сравнений рассчитывается нормированный собственный вектор

ранжирующий альтернативы множества

A. Всем альтернативам-копиям {b

, b

, ..., b

} присваивается

значение нормированного собственного вектора

, соответствующее элементу a

. В результате

получается новый ненормированный вектор приоритетов

всех альтернатив, входящих в множества

A и В. Вектор W

нормируется путем деления каждого значения указанного вектора на сумму всех его

значений.

Метод копирования аналогичен методу сравнения альтернатив относительно стандартов в том плане,

что позволяет не нарушать порядок ранее проранжированных альтернатив при добавлении новых,

являющихся копиями ранее проранжированных альтернатив. Кроме того, число анализируемых

альтернатив при добавлении копий может превышать пороговое значение, равное девяти,

установленное для метода попарного сравнения.

Рассмотрим пример добавления к ранее проранжированным объектам альтернатив-копий.

Допустим, определены три альтернативы A

, А

и А

, для которых экспертом установлена

относительная степень предпочтений по критерию "надежность функционирования системы". Альтер-

нативы сравниваются попарно в матрице, для которой рассчитывается нормированный собственный

вектор, имеющий значения {0,5 0,3 0,2}

. В приведенном векторе указан знак транспонирования — Т, а

порядок значений вектора соответствует весу альтернатив А

, А

и А

. Предположим, что для анализа

поступают две новые альтернативы

, А

, свойства которых по указанному критерию полностью

идентичны свойствам альтернативы

. В этом случае альтернативам-копиям присваиваются веса,

соответствующие весу альтернативы А

,, т. е. А

= 0,2 и А

= 0,2. Новый ненормированный вектор

приоритетов альтернатив принимает следующий вид:

{0,5 0,3 0,2 0,2 0,2}

Значения весов пяти альтернатив после нормирования предыдущего вектора приоритетов имеют

следующий вид:

= 0,35, А

== 0,21, А

= 0,14, A

= 0,14.

Анализ двух векторов приоритетов, характеризующих соответственно множества из трех и пяти

альтернатив, показывает, что добавление альтернатив А

, А

не нарушило порядок приоритетности

альтернатив А

, А

и А

Метод копирования позволяет существенно сократить время экспертов на подготовку исходных

данных для анализа и уменьшить вероятность внесения в них как случайных, так и логических ошибок.

2.6. Многокритериальный выбор на иерархиях с различным числом и составом

альтернатив под критериями

В четвертой модификации рассматривается метод определения векторов приоритетов альтернатив

для иерархий с различным числом и различающимся составом альтернатив под критериями.

В практике принятия решений нередко встречается задача, когда ранжируемые по множеству

критериев альтернативы оцениваются экспертом не по всем критериям. Эта задача характерна для

ситуаций, в которых множество критериев, выделенных для всех рассматриваемых альтернатив,

является избыточным относительно одной или нескольких альтернатив. Таким образом, в рассмат-

риваемом случае эксперт имеет разное количество альтернатив под каждым критерием или под их

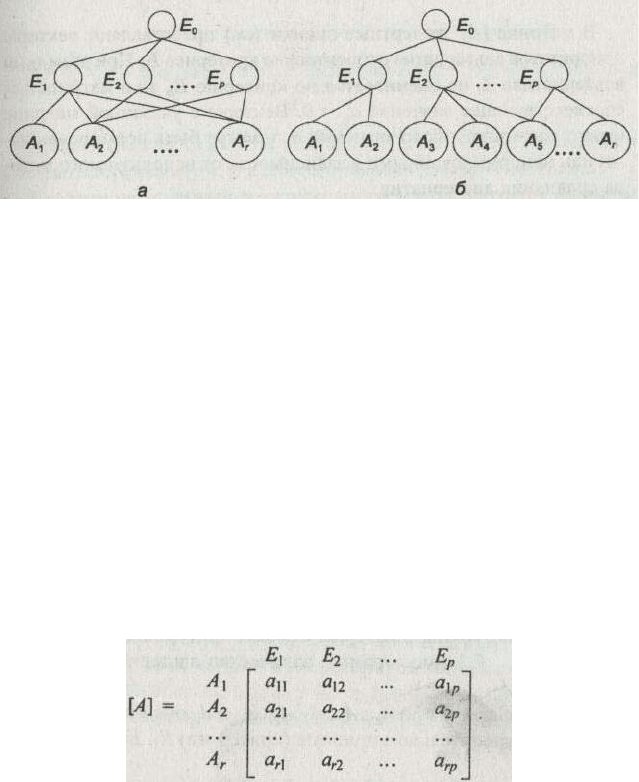
частью. На рис. 2.7 приведены примеры иерархий, в которых каждый критерий E

из множества {Е

, E

... , Е

} имеет разное количество альтернатив из множества {А

,А

, ... ,А

Альтернативы А

и А

; А

, А

; А

и А

оцениваются соответственно относительно элементов

(критериев) Е

, Е

(рис. 2.7а).

Рис. 2.7. Примеры иерархий с разным числом альтернатив под критериями а — синтез; б —

декомпозиция

Рассмотрим методику определения вектора приоритета альтернатив для случая, когда иерархия

имеет один уровень критериев, объединенных фокусом (рис. 2.7 б) с учетом значимости критериев, и

разное количество альтернатив у каждого критерия. Методика предполагает выполнение ряда процедур

по структурированию информации и проведению вычислительных операций.

Процедура 1. Исходная проблема структурируется в виде иерархии, устанавливающей взаимосвязь

между множеством сравниваемых альтернатив {

, A

,... , А

}и множеством критериев {E

, Е

, ... , Е

Процедура 2. На основе иерархической структуры определяется бинарная матрица [В],

устанавливающая соответствие между альтернативами и критериями. Матрица

[В] содержит элементы

= {0,1}. При этом если альтернатива А

оценивается по критерию E

, то b

= 1, в противном случае b

= 0.

Процедура 3.

Осуществляется экспертная оценка альтернатив по соответствующим критериям. Для

этой цели используются метод попарного сравнения, метод сравнения относительно стандартов или

метод копирования. На основе экспертных оценок с учетом матрицы

[В] строится матрица [А]

следующего вида:

В матрице [А] экспертные оценки {a

} представляют векторы приоритетов альтернатив

относительно критериев E

. При этом если альтернатива

не оценивается по критерию Е

, то в матрице

[А] соответствующее значение a

= 0. Векторы в указанной матрице имеют различное число значений

и могут быть нормированными или ненормированными в зависимости от используемого метода

сравнения альтернатив.

Процедура 4. В результате обработки матрицы попарных сравнений критериев Е

определяется

нормированный вектор приоритетов критериев X.

Процедура 5. Формируются структурные критерии S и L, отображаемые соответствующими

диагональными матрицами [S] и [L].

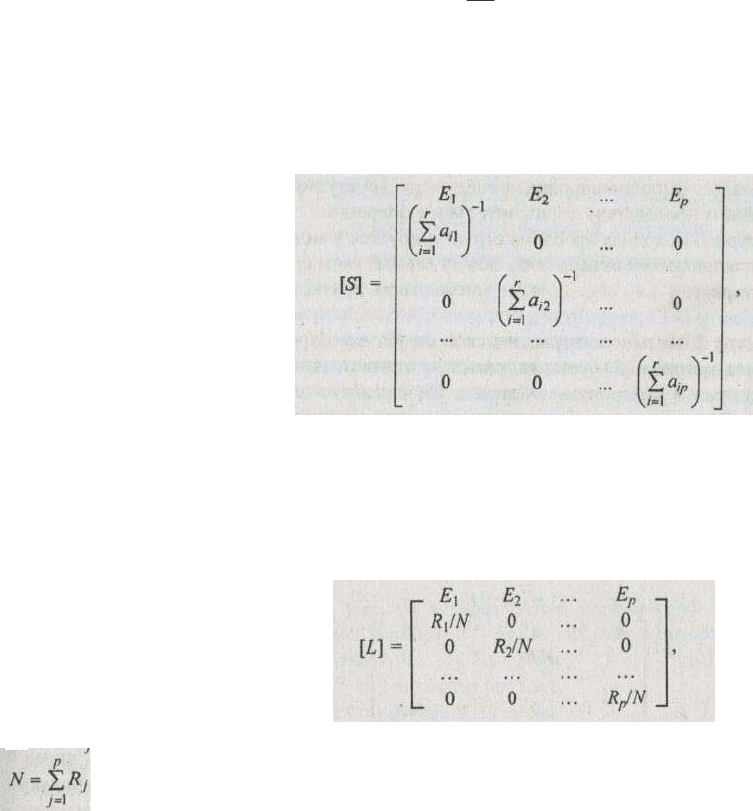
Рассмотрим состав упомянутых матриц.

Матрица [S] имеет следующий вид:

где a

— значения векторов приоритетов из матрицы [А].

С помощью матрицы [S] обеспечивается нормирование векторов приоритетов альтернатив,

образующих матрицу [А], если последняя заполнена методом сравнения относительно стандартов или

копирования без предварительного нормирования.

Матрица [L] имеет следующий вид:

где R

— число альтернатив А

, находящихся под критерием Е

— суммарное число альтернатив, находящихся под всеми критериями.

Здесь следует отметить, что число N в матрице [L] может приниматься равным числу

рассматриваемых альтернатив r, т.е. N= r. При этом на конечный результат способ определения N не

оказывает влияния.

Использование структурного критерия

L позволяет эксперту или ЛПР изменять при необходимости

вес альтернатив, связанных с соответствующими критериями пропорционально отношению

/ N. Этим

обеспечивается повышение приоритета альтернатив, образующих большие группы, и снижение

приоритета альтернатив в группах с их относительно небольшим числом. Здесь имеется в виду, что

группу определяют альтернативы, являющиеся "потомками" по отношению к критерию E

Необходимость в приведенной вычислительной процедуре обусловлена тем, что у критериев-

"родителей" с высоким приоритетом в иерархии может находиться большое число альтернатив-

"потомков", а у критериев-родителей" с низким приоритетом — значительно меньшее число

альтернатив-"потомков", чем в первом случае. Поэтому в этой ситуации желательно повышение

приоритетов альтернатив в большой группе,

поскольку, если альтернатив много, каждая из них получит

меньший составной приоритет, чем каждая альтернатива, входящая в меньшую группу с низким

приоритетом критерия.

На практике возможны также ситуации, прямо противоположные выше охарактеризованной, когда

требуется повысить приоритет так называемых редких альтернатив-"потомков", образующих

относительно критериев-"родителей" маленькие группы. В этом случае структурная матрица

[L]

принимает следующий вид:

Процедура 6.

Определяется вектор приоритетов альтернатив W относительно критериев. Данная

процедура реализуется последовательным перемножением слева направо следующих матриц и

векторов:

а) для случая, когда экспертные оценки в матрице [А] ненормированы:

W=[A] [S][L] X [B]; (2.7)

б) для случая, когда экспертные оценки в матрице [А] нормированы:

W=[A] [L] X [B]. (2.8)

В выражениях (2.7) и (2.8) диагональная матрица [В] предназначена для окончательного

нормирования значений вектора приоритетов альтернатив. Эта матрица имеет следующий вид:

где х

— значение ненормированного вектора приоритетов альтернатив, полученное после

последовательного перемножения слева направо матриц [A], [S], [L] и вектора X ;

r — число альтернатив.

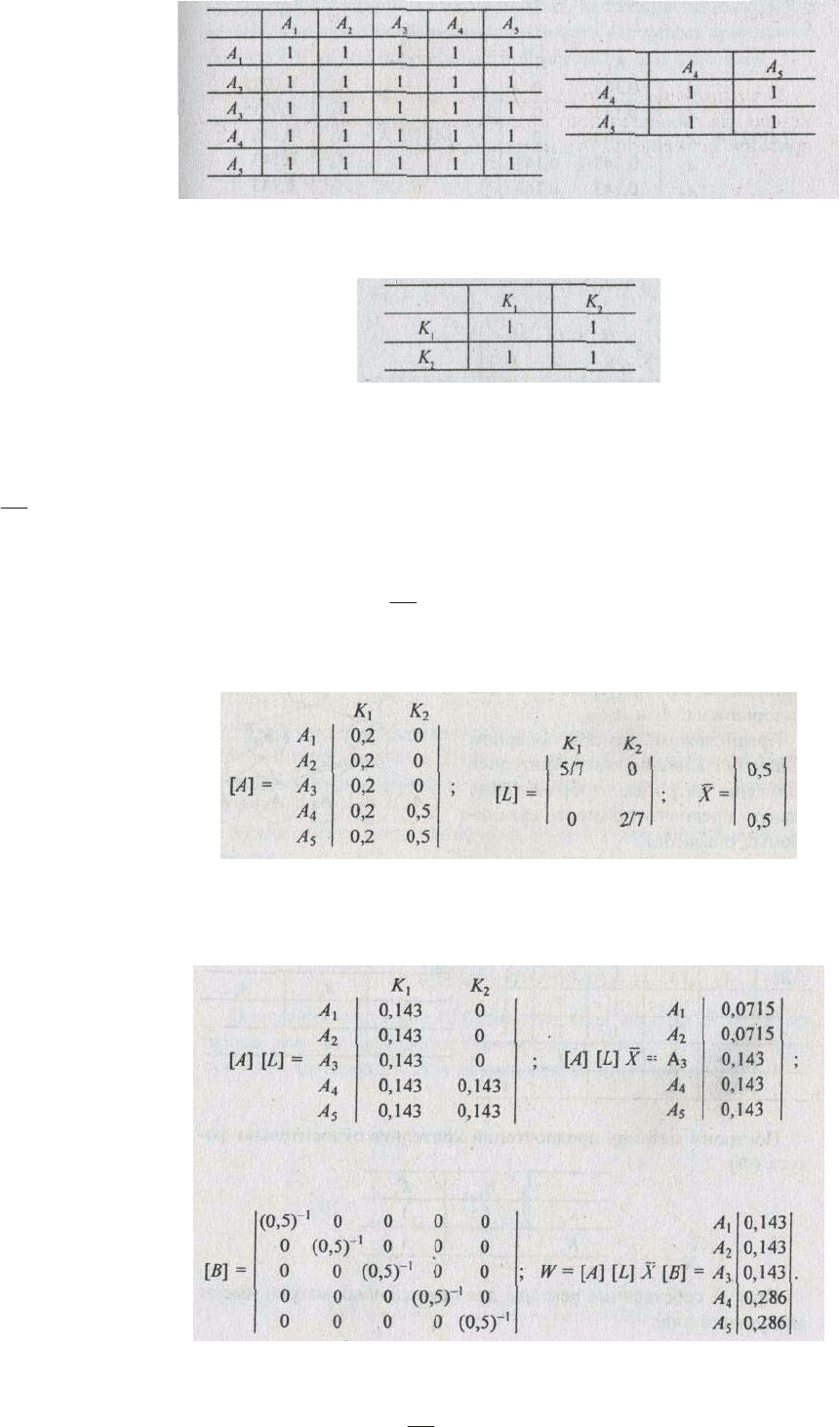
Рассмотрим пример вычисления вектора приоритета альтернатив.

Допустим, имеется иерархическая система (рис. 2.8), включающая корневую вершину — фокус (Ф),

два критерия К

и К

и пять альтернатив A

, ... ,А

. При этом по критерию К

оцениваются все пять

альтернатив, а по критерию К

— две альтернативы: А

и А

Предположим, что при попарном сравнении альтернатив и критериев получены матрицы,

отображающие равную предпочтительность сравниваемых объектов.

Матрицы предпочтений альтернатив относительно критериев K

и K

соответственно примут вид:

Построим матрицу предпочтений критериев относительно фокуса (Ф):

Правые собственные векторы для приведенных матриц имеют следующий вид:



W = {0,2 0,2 0,2 0,2 0,2}

— приоритет альтернатив по критерию K

;



= {0,5 0,5}

— приоритет альтернатив по критерию К

;

X = {0,5 0,5}

— приоритет критериев относительно фокуса Ф.

Поскольку векторы приоритетов альтернатив относительно критериев K

и К

нормированы,

результирующий вектор рассчитывается по формуле (2.8).

При этом матрицы [А] и [L] и вектор X с учетом ранее выполненных расчетов имеют следующий

вид:

Производя последовательные перемножения матриц и вектора слева направо, получим следующие

результаты:

Следует отметить, что при неучете структурного критерия L результирующий вектор приоритетов

альтернатив имеет следующий вид:

W'=[A] X= {0,1 0,1 0,1 0,35 0,35}