Андреева Е.В., Егоров Ю.Е. Вычислительная геометрия на плоскости
Подождите немного. Документ загружается.

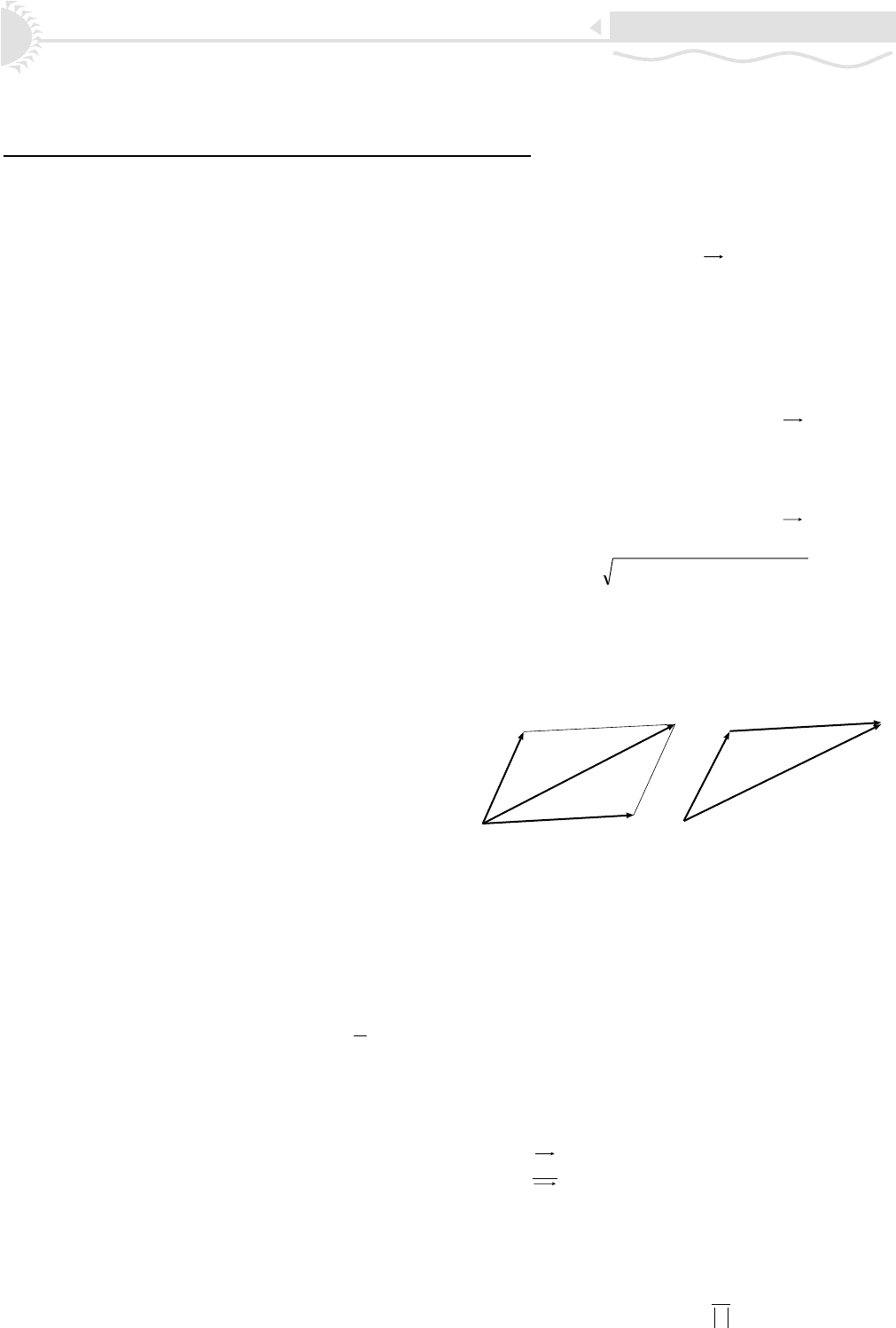
2002 ¹ 39 ÈÍÔÎÐÌÀÒÈÊÀ
26
ÇÀÄÀ×È
Âû÷èñëèòåëüíàÿ ãåîìåòðèÿ ýòî ðàçäåë èíôîðìà-
òèêè, èçó÷àþùèé àëãîðèòìû ðåøåíèÿ ãåîìåòðè÷åñêèõ
çàäà÷. Òàêèå çàäà÷è âîçíèêàþò â êîìïüþòåðíîé ãðàôè-
êå, ïðîåêòèðîâàíèè èíòåãðàëüíûõ ñõåì, òåõíè÷åñêèõ
óñòðîéñòâ è äð. Èñõîäíûìè äàííûìè â òàêîãî ðîäà çà-
äà÷àõ ìîãóò áûòü ìíîæåñòâî òî÷åê, íàáîð îòðåçêîâ,
ìíîãîóãîëüíèê è ò.ï. Ðåçóëüòàòîì ìîæåò áûòü ëèáî îò-
âåò íà êàêîé-òî âîïðîñ (òèïà ïåðåñåêàþòñÿ ëè ýòè
ïðÿìûå), ëèáî êàêîé-òî ãåîìåòðè÷åñêèé îáúåêò (íà-
ïðèìåð, íàèìåíüøèé âûïóêëûé ìíîãîóãîëüíèê, ñîäåð-
æàùèé çàäàííûå òî÷êè) [1].
 Èíôîðìàòèêå ¹ 14 çà ýòîò ãîä áûëà îïóáëè-
êîâàíà ñòàòüÿ îäíîãî èç àâòîðîâ, ïîñâÿùåííàÿ çàäà-
÷àì âû÷èñëèòåëüíîé ãåîìåòðèè â îëèìïèàäàõ ïî èí-
ôîðìàòèêå.  ÷àñòíîñòè, òàì áûë ñôîðìóëèðîâàí ðÿä
ýëåìåíòàðíûõ ïîäçàäà÷, íà êîòîðûå îïèðàåòñÿ ðåøå-
íèå áîëüøèíñòâà çàäà÷ âû÷èñëèòåëüíîé ãåîìåòðèè.
Îäíàêî çàíÿòèÿ äàæå ñ ìàòåìàòè÷åñêè õîðîøî ïîäãî-
òîâëåííûìè ó÷àùèìèñÿ ñòàðøèõ êëàññîâ ïîêàçàëè, ÷òî
ðåøåíèå òàêèõ ïîäçàäà÷ âûçûâàåò ó íèõ áîëüøîå çàò-
ðóäíåíèå. Çàäà÷à ëèáî ñòàâèò èõ â òóïèê, ëèáî âûá-
ðàííûé ëîáîâîé ñïîñîá ðåøåíèÿ íàñòîëüêî ñëîæåí,
÷òî äîâåñòè åãî äî êîíöà áåç îøèáîê ó÷àùèåñÿ íå
ìîãóò. Àíàëèç ðåçóëüòàòîâ ðåøåíèÿ ãåîìåòðè÷åñêèõ
çàäà÷ íà âñåðîññèéñêèõ îëèìïèàäàõ ïî èíôîðìàòèêå
ïðèâîäèò ê òåì æå âûâîäàì. Òàêóþ ñèòóàöèþ ìû ñ÷è-
òàåì ïîïðàâèìîé. Öåëü íàñòîÿùåé ñòàòüè ïîêàçàòü
ïîäõîäû ê ðåøåíèþ ãåîìåòðè÷åñêèõ çàäà÷ íà ïëîñêî-
ñòè, êîòîðûå ïîçâîëÿþò äîñòàòî÷íî áûñòðî è ìàêñè-
ìàëüíî ïðîñòî ïîëó÷àòü ðåøåíèÿ áîëüøèíñòâà ýëåìåí-
òàðíûõ ïîäçàäà÷.
Âåêòîðû è êîîðäèíàòû
×òîáû ïðèìåíÿòü ìåòîäû âû÷èñëèòåëüíîé ãåîìåòðèè,
íåîáõîäèìî ãåîìåòðè÷åñêèå îáðàçû ïåðåâåñòè íà ÿçûê
÷èñåë. Áóäåì ñ÷èòàòü, ÷òî íà ïëîñêîñòè çàäàíà äåêàðòîâà
ñèñòåìà êîîðäèíàò (ÑÊ). Îáùåïðèíÿòî âûáèðàòü êî-
îðäèíàòíûå îñè òàê, ÷òîáû ïîâîðîò íà óãîë
2
π
, ïðè êî-
òîðîì îñü Ox ñîâìåùàåòñÿ ñ îñüþ Oy, ïðîèñõîäèë ïðî-
òèâ ÷àñîâîé ñòðåëêè. Òàêóþ ÑÊ íàçûâàþò ïðàâîé.  äàëü-
íåéøåì ïîäðàçóìåâàåòñÿ, ÷òî íàøà ÑÊ ïðàâàÿ. Â òàêîé
ÑÊ íàïðàâëåíèå ïîâîðîòà ïðîòèâ ÷àñîâîé ñòðåëêè íàçû-
âàåòñÿ ïîëîæèòåëüíûì.
Òåïåðü ãåîìåòðè÷åñêèå îáúåêòû ïîëó÷àþò àíàëèòè÷å-
ñêîå âûðàæåíèå. Òàê, ÷òîáû çàäàòü îòðåçîê, äîñòàòî÷íî
óêàçàòü êîîðäèíàòû åãî êîíöîâ. Ïðÿìóþ ìîæíî çàäàòü,
óêàçàâ ïàðó åå òî÷åê, ëèáî êîîðäèíàòàìè îäíîé åå òî÷-
êè è âåêòîðîì, õàðàêòåðèçóþùèì íàïðàâëåíèå ýòîé
ïðÿìîé, è ò.ä. Âîîáùå ïðè ðåøåíèè çàäà÷ îñíîâíûì
èíñòðóìåíòîì äëÿ íàñ áóäóò âåêòîðû. Íàïîìíèì ïîýòî-
ìó íåêîòîðûå ñâåäåíèÿ î íèõ.
Âû÷èñëèòåëüíàÿ ãåîìåòðèÿ íà ïëîñêîñòè
Å.Â. Àíäðååâà, Þ.Å. Åãîðîâ,
Ìîñêâà
Îòðåçîê AB, ó êîòîðîãî òî÷êó A ñ÷èòàþò íà÷àëîì (òî÷-
êîé ïðèëîæåíèÿ), à òî÷êó B êîíöîì, íàçûâàþò âåê-
òîðîì AB è îáîçíà÷àþò ëèáî
AB
, ëèáî æèðíîé ñòðî÷-
íîé ëàòèíñêîé áóêâîé, íàïðèìåð, a. Äëÿ îáîçíà÷åíèÿ
äëèíû âåêòîðà (òî åñòü äëèíû ñîîòâåòñòâóþùåãî îò-
ðåçêà) áóäåì ïîëüçîâàòüñÿ ñèìâîëîì ìîäóëÿ (íàïðè-
ìåð, |a|). Äâà âåêòîðà íàçûâàþòñÿ ðàâíûìè, åñëè îíè
ñîâìåùàþòñÿ ïàðàëëåëüíûì ïåðåíîñîì.
Ïóñòü òî÷êè A è B èìåþò êîîðäèíàòû (x
1
, y
1
) è (x
2
, y
2
)
ñîîòâåòñòâåííî. Êîîðäèíàòàìè âåêòîðà
AB
íàçûâàåòñÿ
ïàðà ÷èñåë (x
2
x
1
, y
2
y
1
). Íàîáîðîò, åñëè âåêòîð
èìååò êîîðäèíàòû (x, y) è ïðèëîæåí ê òî÷êå (x
1
, y
1
),
òî ëåãêî âû÷èñëèòü êîîðäèíàòû (x
2
, y
2
) åãî êîíöà:
x
2
= x
1
+ x, y
2
= y
1
+ y. Äëèíà âåêòîðà
AB
ïî òåîðåìå
Ïèôàãîðà ðàâíà
2
12
2
12
)()(
yyxx
+
. Ðàâåíñòâî
äâóõ âåêòîðîâ a = (a
x
, a
y
) è b = (b
x
, b
y
) ýêâèâàëåíòíî
ðàâåíñòâó èõ ñîîòâåòñòâóþùèõ êîîðäèíàò: a
x
= b
x
, a
y
= b
y
.
Âåêòîðû ìîæíî ñêëàäûâàòü è óìíîæàòü íà ÷èñëà.
Ñëîæåíèå âåêòîðîâ ïðîèçâîäèòñÿ ïî ïðàâèëó òðåóãîëü-
íèêà èëè ïî ïðàâèëó ïàðàëëåëîãðàììà (ðèñ. 1).
a
b
a+b
a
b
a+b
Ðèñ. 1
Ïîä ðàçíîñòüþ âåêòîðîâ a è b ïîíèìàþò ñóììó
âåêòîðà a ñ âåêòîðîì, ïðîòèâîïîëîæíûì âåêòîðó b
(ò.å. ïðîòèâîïîëîæíî íàïðàâëåííûì è ñîâïàäàþùèì ñ
íèì ïî äëèíå). Ïðè óìíîæåíèè âåêòîðà a íà ÷èñëî t
ïîëó÷àåòñÿ âåêòîð, èìåþùèé äëèíó |t | ⋅ |a|; åãî íà-
ïðàâëåíèå ñîâïàäàåò ñ íàïðàâëåíèåì a, åñëè t > 0, è
ïðîòèâîïîëîæíî åìó, åñëè t < 0. Ýòî ïîçâîëÿåò íàì
ââåñòè îòíîøåíèå êîëëèíåàðíûõ âåêòîðîâ (ò.å. ñîíàï-
ðàâëåííûõ èëè ïðîòèâîïîëîæíî íàïðàâëåííûõ), ïî-
íèìàÿ ïîä íèì êîýôôèöèåíò èõ ïðîïîðöèîíàëüíîñ-
òè. Ñ ïîìîùüþ òàêîãî îòíîøåíèÿ óäîáíî îïèñûâàòü
ïîðÿäîê ðàñïîëîæåíèÿ òî÷åê íà ïðÿìîé. Íàïðèìåð,
óñëîâèå
AC
AB
< 0 îçíà÷àåò, ÷òî òî÷êè A, B è C ëåæàò
íà îäíîé ïðÿìîé, ïðè÷åì òî÷êà A ëåæèò ìåæäó B è C.
Îòìåòèì åùå, ÷òî âåêòîð, ñîíàïðàâëåííûé ñ äàííûì
âåêòîðîì a è èìåþùèé çàäàííóþ äëèíó l, ìîæíî
âûðàçèòü ñëåäóþùèì îáðàçîì:
a
a
l
. Â äàëüíåéøåì ìû
2002 ¹ 39 ÈÍÔÎÐÌÀÒÈÊÀ
27
ÇÀÄÀ×È
íåîäíîêðàòíî áóäåì ýòèì ïîëüçîâàòüñÿ. Â êîîðäèíà-
òàõ ïåðå÷èñëåííûå îïåðàöèè íàä âåêòîðàìè çàïèñû-
âàþòñÿ òàê:
åñëè a = (a
x
, a
y
) è b = (b
x
, b
y
),
òî a + b = (a
x
+ b
x
, a
y
+ b
y
),
a b = (a
x
b
x
, a
y
b
y
) è t ⋅ a = (t ⋅ a
x
, t ⋅ a
y
).
Ñêàëÿðíûì ïðîèçâåäåíèåì äâóõ íåíóëåâûõ âåêòîðîâ
a = (x
1
, y
1
) è b = (x
2
, y
2
) íàçûâàåòñÿ ÷èñëî
(a, b) = |a | ⋅ |b | ⋅ cos ϕ,
ãäå ϕ óãîë ìåæäó ýòèìè âåêòîðàìè.
 êîîðäèíàòàõ îíî âû÷èñëÿåòñÿ òàê:
(a, b) = x
1
x
2
+ y
1
y
2
.
Êàê âèäíî èç ôîðìóë, ñêàëÿðíîå ïðîèçâåäåíèå ìîæíî
èñïîëüçîâàòü äëÿ íàõîæäåíèÿ óãëà ìåæäó âåêòîðàìè. Â
÷àñòíîñòè, äâà íåíóëåâûõ âåêòîðà ïåðïåíäèêóëÿðíû òîãäà
è òîëüêî òîãäà, êîãäà èõ ñêàëÿðíîå ïðîèçâåäåíèå ðàâíî
íóëþ (
0
2
=
π
cos
). Òàê êàê cos ϕ ïîëîæèòåëåí äëÿ îñò-
ðûõ óãëîâ è îòðèöàòåëåí äëÿ òóïûõ, óãîë ìåæäó âåêòîðà-
ìè îñòðûé (òóïîé) â òîì è òîëüêî òîì ñëó÷àå, êîãäà èõ
ñêàëÿðíîå ïðîèçâåäåíèå ïîëîæèòåëüíî (îòðèöàòåëüíî).
Óãîë ìåæäó âåêòîðàìè
Ïóñòü a è b äâà íåíóëåâûõ âåêòîðà, îòëîæåííûå
îò îäíîé òî÷êè.  øêîëüíîì êóðñå ãåîìåòðèè ïîä óãëîì
ìåæäó âåêòîðàìè ïîíèìàåòñÿ ìåíüøèé èç äâóõ óãëîâ
ìåæäó ëó÷àìè, íà êîòîðûõ ëåæàò âåêòîðû a è b. Çíà÷å-
íèå òàêîãî óãëà âñåãäà íàõîäèòñÿ â ïðîìåæóòêå [0; π].
Äëÿ âû÷èñëåíèé ÷àñòî áîëåå óäîáíûì îêàçûâàåòñÿ
ïîíÿòèå îðèåíòèðîâàííîãî óãëà, ò.å. óãëà, ó÷èòûâàþùå-
ãî âçàèìíîå ðàñïîëîæåíèå âåêòîðîâ. Çíà÷åíèå îðèåí-
òèðîâàííîãî óãëà ïî àáñîëþòíîé âåëè÷èíå ðàâíî îáû÷-
íîìó óãëó ìåæäó âåêòîðàìè. Îðèåíòèðîâàííûé óãîë
ìåæäó âåêòîðàìè a è b ïîëîæèòåëüíûé, åñëè ïîâîðîò
îò âåêòîðà a ê âåêòîðó b ñîâåðøàåòñÿ â ïîëîæèòåëüíîì
íàïðàâëåíèè (â íàøåé ÑÊ ïðîòèâ ÷àñîâîé ñòðåëêè), è
îòðèöàòåëüíûé â äðóãîì ñëó÷àå. Ãîâîðÿò òàêæå, ÷òî
ïàðà âåêòîðîâ a è b ïîëîæèòåëüíî (îòðèöàòåëüíî) îðè-
åíòèðîâàíà. Òàêèì îáðàçîì, âåëè÷èíà îðèåíòèðîâàííîãî
óãëà çàâèñèò îò ïîðÿäêà ïåðå÷èñëåíèÿ âåêòîðîâ è ìîæåò
ïðèíèìàòü çíà÷åíèÿ â èíòåðâàëå (π; π]. Íà ðèñ. 2 îðè-
åíòèðîâàííûå óãëû ìåæäó âåêòîðàìè
OA
è
OB
è ìåæäó
âåêòîðàìè
OB
è
OA
ðàâíû ïî ìîäóëþ, íî ïåðâûé èç íèõ
îòðèöàòåëüíûé, à âòîðîé ïîëîæèòåëüíûé.
Äëÿ ëþáûõ âåêòîðîâ
OA
,
OB
è
OC
ëåãêî âû÷èñëèòü
âåëè÷èíó îðèåíòèðîâàííîãî óãëà AOB, çíàÿ âåëè÷èíû óã-
ëîâ AOC è COB: îíà ðàâíà èõ ñóììå ñ ó÷åòîì çíàêîâ.
Íàïðèìåð, ïðè òàêîì ðàñïîëîæåíèè âåêòîðîâ, êàê íà
ðèñ. 2, óãîë AOC âîéäåò â ñóììó ñî çíàêîì ïëþñ, à óãîë
COB ñ ìèíóñîì. Ìîæåò ñëó÷èòüñÿ, ÷òî ïðè ñóììè-
ðîâàíèè äâóõ ïîëîæèòåëüíûõ (äâóõ îòðèöàòåëüíûõ)
óãëîâ ðåçóëüòàò ïðåâçîéäåò π ïî ìîäóëþ. Òîãäà, ÷òîáû
ïîëó÷èòü ïðàâèëüíîå çíà÷åíèå óãëà, íóæíî îòíÿòü (äî-
áàâèòü) 2π. Çàìå÷àòåëüíî, ÷òî ïðè ýòîì íàì íå ïðèäåòñÿ
ðàññìàòðèâàòü ðàçëè÷íûå ñëó÷àè âçàèìíîãî ðàñïîëîæå-
íèÿ âåêòîðîâ. Â ýòîì è ñîñòîèò ïðåèìóùåñòâî èñïîëüçî-
âàíèÿ îðèåíòèðîâàííûõ óãëîâ.
B
A
C
O
Ðèñ. 2
Êàê, çíàÿ êîîðäèíàòû âåêòîðîâ, íàéòè óãîë ìåæäó
íèìè? Î÷åâèäíûé ñïîñîá ñëåäóåò èç ôîðìóëû äëÿ ñêà-
ëÿðíîãî ïðîèçâåäåíèÿ:
ba
ba
⋅
=ϕ
),(
cos
. Îäíàêî ïðè ýòîì
ïîëó÷èòñÿ çíà÷åíèå íåîðèåíòèðîâàííîãî óãëà è ÷àñòü èí-
ôîðìàöèè (âîçìîæíî, ïîëåçíàÿ) áóäåò íàìè ïîòåðÿíà.
Êðîìå òîãî, èñïîëüçîâàíèå ýòîé ôîðìóëû äëÿ ïðîãðàììè-
ðîâàíèÿ íå âñåãäà óäîáíî. Íàïðèìåð, â ÿçûêå Ïàñêàëü,
êàê è â ðÿäå äðóãèõ ÿçûêîâ ïðîãðàììèðîâàíèÿ, èç îáðàò-
íûõ òðèãîíîìåòðè÷åñêèõ ôóíêöèé ðåàëèçîâàíà òîëüêî ôóíê-
öèÿ arctg ϕ. Ìû ïîêàæåì, êàê íàéòè óãîë èíà÷å, ïîñëå
òîãî, êàê ïîçíàêîìèìñÿ ñ îðèåíòèðîâàííîé ïëîùàäüþ.
Îðèåíòèðîâàííàÿ ïëîùàäü
Îðèåíòèðîâàííàÿ ïëîùàäü òðåóãîëüíèêà ýòî åãî
îáû÷íàÿ ïëîùàäü, ñíàáæåííàÿ çíàêîì. Çíàê ó îðèåíòè-
ðîâàííîé ïëîùàäè òðåóãîëüíèêà ABC òàêîé æå, êàê ó
îðèåíòèðîâàííîãî óãëà ìåæäó âåêòîðàìè
AB
è
AC
. Òî
åñòü åå çíàê çàâèñèò îò ïîðÿäêà ïåðå÷èñëåíèÿ âåðøèí.
Íà ðèñ. 2 òðåóãîëüíèê ABC ïðÿìîóãîëüíûé. Åãî îðè-
åíòèðîâàííàÿ ïëîùàäü ðàâíà
||| |
2
AB AC
⋅
KK H KKKH
(îíà áîëüøå
íóëÿ, òàê êàê ïàðà
AB
,
AC
îðèåíòèðîâàíà ïîëîæèòåëü-
íî). Ýòó æå âåëè÷èíó ìîæíî âû÷èñëèòü äðóãèì ñïîñî-
áîì. Ïóñòü O ïðîèçâîëüíàÿ òî÷êà ïëîñêîñòè. Íà íà-
øåì ðèñóíêå ïëîùàäü òðåóãîëüíèêà ABC ïîëó÷èòñÿ, åñëè
èç ïëîùàäè òðåóãîëüíèêà OBC âû÷åñòü ïëîùàäè OAB è
OCA. Òàêèì îáðàçîì, íóæíî ïðîñòî ñëîæèòü îðèåíòèðî-
âàííûå ïëîùàäè òðåóãîëüíèêîâ OAB, OBC è OCA. Ýòî
ïðàâèëî ðàáîòàåò ïðè ëþáîì âûáîðå òî÷êè O.
Òî÷íî òàê æå äëÿ âû÷èñëåíèÿ ïëîùàäè ëþáîãî
ìíîãîóãîëüíèêà A
1
A
2
A
n
íóæíî ñëîæèòü îðèåíòèðî-
âàííûå ïëîùàäè òðåóãîëüíèêîâ OA
1
A
2
, OA
2
A
3
, , OA
n
A
1
(ðèñ. 3).  ñóììå ïîëó÷èòñÿ ïëîùàäü ìíîãîóãîëüíèêà,
âçÿòàÿ ñî çíàêîì ïëþñ, åñëè ïðè îáõîäå ëîìàíîé A
1
A
2
A
n
âíóòðåííîñòü ìíîãîóãîëüíèêà íàõîäèòñÿ ñëåâà, è ñî çíà-
êîì ìèíóñ, åñëè îíà íàõîäèòñÿ ñïðàâà. Îíà è íàçûâàåò-
ñÿ îðèåíòèðîâàííîé ïëîùàäüþ ìíîãîóãîëüíèêà
A
1
A
2
A
n
. Òàêèì îáðàçîì, äëÿ ïðàâîé ÑÊ îðèåíòèðî-
2002 ¹ 39 ÈÍÔÎÐÌÀÒÈÊÀ
28
ÇÀÄÀ×È
âàííàÿ ïëîùàäü îêàæåòñÿ ïîëîæèòåëüíîé ïðè îáõîäå
ãðàíèöû ìíîãîóãîëüíèêà ïðîòèâ ÷àñîâîé ñòðåëêè.
O
A
1
A
2
A
3
A
4
A
5
Ðèñ. 3
Èòàê, âû÷èñëåíèå ïëîùàäè ìíîãîóãîëüíèêà ñâåëîñü
ê íàõîæäåíèþ îðèåíòèðîâàííîé ïëîùàäè òðåóãîëüíè-
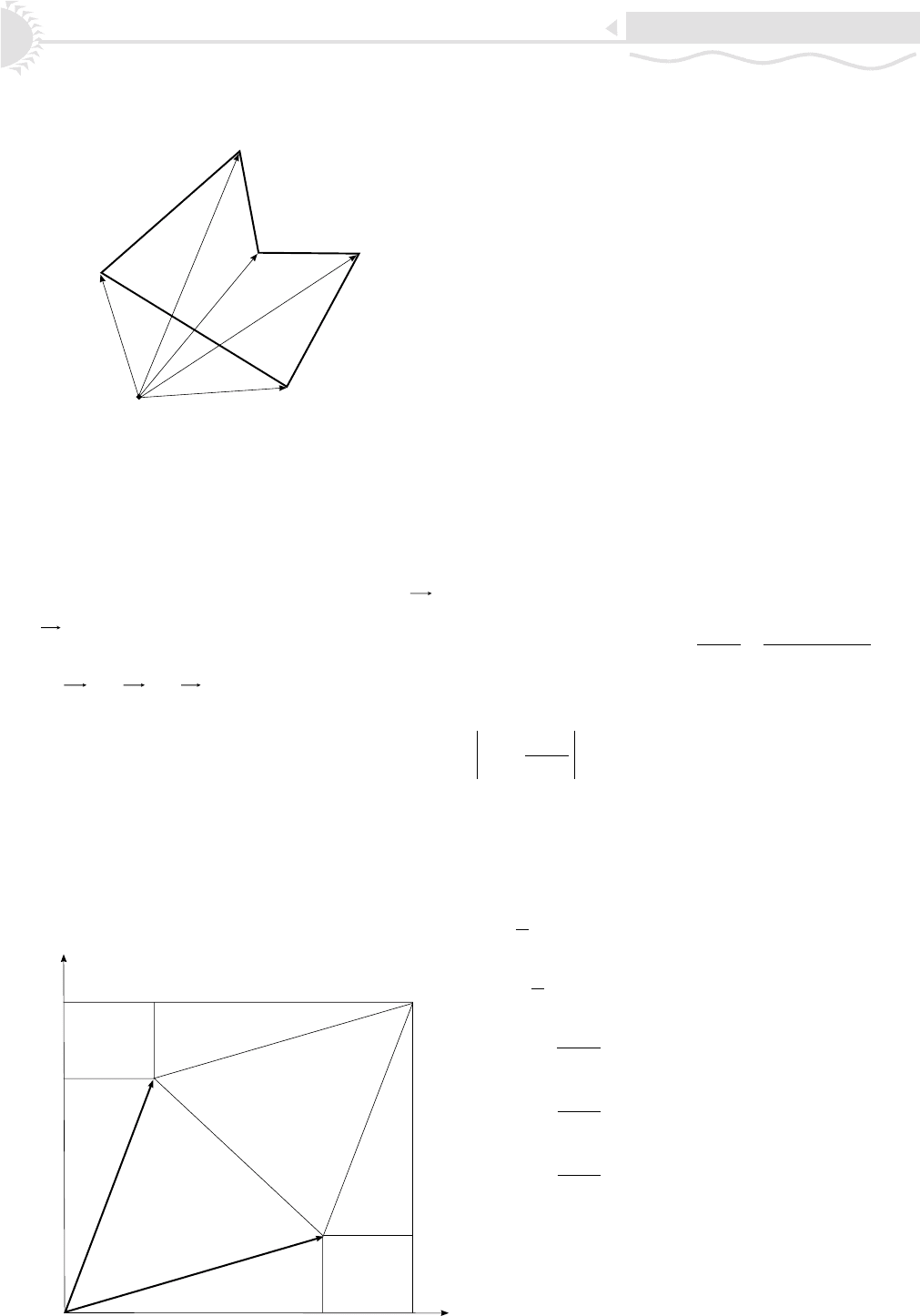
êà. Ïîñìîòðèì, êàê âûðàçèòü åå â êîîðäèíàòàõ. Ïóñòü
S îðèåíòèðîâàííàÿ ïëîùàäü òðåóãîëüíèêà, ïîñòðîåí-
íîãî íà âåêòîðàõ a = (x
1
, y
1
) è b = (x
2
, y
2
). Âû÷èñëèì
åå äëÿ êîíêðåòíîãî ðàñïîëîæåíèÿ âåêòîðîâ (ðèñ. 4). Âå-
ëè÷èíà S çäåñü ïîëîæèòåëüíà (ïàðà âåêòîðîâ a =
OA
è
b =
OB
ïîëîæèòåëüíî îðèåíòèðîâàíà). Äîñòðîèì íàø
òðåóãîëüíèê äî ïàðàëëåëîãðàììà OACB ïëîùàäè 2S
(çäåñü
OC
=
OA
+
OB
). Òîãäà ïëîùàäü ïðÿìîóãîëü-
íèêà OC
1
CC
2
ðàâíà
|OC
1
| ⋅ |OC
2
| = (x
1
+ x
2
)(y
1
+ y
2
) =
= 2S + 2S
1
+ 2S
2
+ 2S
3
=
= 2S + x
1
y
1
+ x
2
y
2
+ 2x
2
y
1
(çäåñü S
1
, S
2
, S
3
îáû÷íûå íåîðèåíòèðîâàííûå ïëî-
ùàäè). Ðàñêðûâ ñêîáêè â ëåâîé ÷àñòè ðàâåíñòâà è âû-
ðàçèâ 2S, ïîëó÷èì
2S = x
1
y
2
x
2
y
1
. (1)
yy
12
+
y
2
C
2
C
C
1
A
B
O
x
1
xx
12
+
S
S
3
S
1
S
2
S
S
2
S
3
S
1
b
a
Ðèñ. 4
Íåòðóäíî óáåäèòüñÿ, ÷òî è ïðè äðóãèõ âàðèàíòàõ ðàñ-
ïîëîæåíèÿ âåêòîðîâ ôîðìóëà (1) òàêæå îñòàåòñÿ ñïðà-
âåäëèâîé. Òàêèì îáðàçîì, îðèåíòèðîâàííàÿ ïëîùàäü ïà-
ðàëëåëîãðàììà, ïîñòðîåííîãî íà âåêòîðàõ a = (x
1
, y
1
) è
b = (x
2
, y
2
), ðàâíà x
1
y
2
x
2
y
1
.
Âåëè÷èíà x
1
y
2
x
2
y
1
íàçûâàåòñÿ êîñûì (èëè ïñåâäî-
ñêàëÿðíûì) ïðîèçâåäåíèåì âåêòîðîâ a è b. Äëÿ êîñî-
ãî ïðîèçâåäåíèÿ ìû áóäåì óïîòðåáëÿòü îáîçíà÷åíèå
[a, b]. Åãî íàçâàíèå ñâÿçàíî ñî ñâîéñòâîì êîñîé ñèì-
ìåòðèè: [a, b] = [b, a] (â ëèòåðàòóðå ýòî îáîçíà÷å-
íèå èñïîëüçóåòñÿ äëÿ âåêòîðíîãî ïðîèçâåäåíèÿ, íî â îò-
ëè÷èå îò ïîñëåäíåãî êîñîå ïðîèçâåäåíèå ñêàëÿð). Òàê
êàê íåîðèåíòèðîâàííàÿ ïëîùàäü ïàðàëëåëîãðàììà, ïî-
ñòðîåííîãî íà âåêòîðàõ a è b, ðàâíà |a| ⋅ |b| ⋅ |sin ϕ|, à
çíàê sin ϕ ñîâïàäàåò ñî çíàêîì îðèåíòèðîâàííîãî óãëà
ϕ, òî [a, b] = |a| ⋅ |b | ⋅ sin ϕ. Âåëè÷èíà [a, b] áîëüøå
íóëÿ, åñëè ïàðà âåêòîðîâ a è b ïîëîæèòåëüíî îðèåíòè-
ðîâàíà, è ìåíüøå íóëÿ â ïðîòèâíîì ñëó÷àå. Êîñîå ïðî-
èçâåäåíèå íåíóëåâûõ âåêòîðîâ ðàâíî íóëþ òîãäà è òîëü-
êî òîãäà, êîãäà îíè êîëëèíåàðíû (sin 0 = sin π = 0).
Òåïåðü, êàê è îáåùàëè, íàéäåì â êîîðäèíàòàõ óãîë
ìåæäó äâóìÿ âåêòîðàìè. Ïóñòü ϕ îðèåíòèðîâàííûé
óãîë ìåæäó âåêòîðàìè a = (x
1
, y
1
) è b = (x
2
, y
2
). Ñîïî-
ñòàâëÿÿ ôîðìóëû äëÿ ñêàëÿðíîãî è êîñîãî ïðîèçâåäåíèé
ýòèõ âåêòîðîâ, èìååì
2
1
2
1
1
22
1
),(
],[
tg
yyxx
yxyx
+
==ϕ
ba
ba
. Çíàÿ
òàíãåíñ óãëà ìåæäó âåêòîðàìè, ìû ëåãêî íàéäåì óãîë
ìåæäó ïðÿìûìè, íà êîòîðûõ ëåæàò a è b: îí ðàâåí
),(
],[
arctg
ba
ba
. ×òîáû ïîëó÷èòü íåïîñðåäñòâåííî ñàì óãîë
ìåæäó âåêòîðàìè, îñòàëîñü âûÿñíèòü, îñòðûé îí èëè òó-
ïîé. Ýòî ìû îïðåäåëèì ïî çíàêó ñêàëÿðíîãî ïðîèçâåäå-
íèÿ. Ó÷òåì åùå, ÷òî çíàê îðèåíòèðîâàííîãî óãëà ñîâ-
ïàäàåò ñî çíàêîì êîñîãî ïðîèçâåäåíèÿ. Òîãäà îêîí÷à-
òåëüíî èìååì:
ϕ =
2
π
, åñëè (a, b) = 0, [a, b] > 0;
ϕ =
2
π
, åñëè (a, b) = 0, [a, b] < 0;
ϕ =
),(
],[
arctg
ba
ba
, åñëè (a, b) > 0; (2)
ϕ =
),(
],[
arctg
ba
ba
+ π, åñëè (a, b) < 0, [a, b] ≥ 0;
ϕ =
),(
],[
arctg
ba
ba
π, åñëè (a, b) < 0, [a, b] < 0.
Âåëè÷èíà îáû÷íîãî óãëà ðàâíà ìîäóëþ çíà÷åíèÿ îðè-
åíòèðîâàííîãî óãëà.
Îòìåòèì, ÷òî âñå ñêàçàííîå îá îðèåíòèðîâàííûõ óã-
ëàõ è ïëîùàäÿõ îòíîñèëîñü ê ïðàâîé ÑÊ. Ìîæåò ñòàòü-
ñÿ, ÷òî äëÿ êîíêðåòíîé çàäà÷è óäîáíåå ââåñòè ëåâóþ ÑÊ.
Ê ïðèìåðó, êîîðäèíàòû ïèêñåëåé íà ýêðàíå ìîíèòîðà
äàþòñÿ èìåííî â ëåâîé ÑÊ (îñü àáñöèññ ñìîòðèò âïðàâî,
2002 ¹ 39 ÈÍÔÎÐÌÀÒÈÊÀ
29
ÇÀÄÀ×È
îñü îðäèíàò âíèç). Ïðè òàêîì âûáîðå îñåé ïîëîæè-
òåëüíûì ÿâëÿåòñÿ ïîâîðîò ïî ÷àñîâîé ñòðåëêå. Ñ ýòîé ïî-
ïðàâêîé âñå âûøåèçëîæåííîå ïðèìåíèìî è ê ëåâîé ÑÊ.
Óðàâíåíèÿ ëèíèé
1.1. Óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç äâå ðàç-
ëè÷íûå òî÷êè, çàäàííûå ñâîèìè êîîðäèíàòàìè.
Ïóñòü íà ïðÿìîé çàäàíû äâå íåñîâïàäàþùèå òî÷êè: P
1
ñ êîîðäèíàòàìè (x
1
, y
1
) è P
2
c êîîðäèíàòàìè (x
2
, y
2
).
Ñîîòâåòñòâåííî âåêòîð ñ íà÷àëîì â òî÷êå P
1
è êîíöîì â
òî÷êå P
2
èìååò êîîðäèíàòû (x
2
x
1
, y
2
y
1
). Åñëè
P(x, y) ïðîèçâîëüíàÿ òî÷êà íà íàøåé ïðÿìîé, òî êî-
îðäèíàòû âåêòîðà
PP
1
ðàâíû (x x
1
, y y
1
). Ñ ïîìî-
ùüþ êîñîãî ïðîèçâåäåíèÿ óñëîâèå êîëëèíåàðíîñòè âåê-
òîðîâ
PP
1
è
21
PP
ìîæíî âûðàçèòü òàê:
],[
2
11
PPPP
= 0,
ò.å. (x x
1
)(y
2
y
1
) (y y
1
)(x
2
x
1
) = 0 (3)
èëè
(y
2
y
1
)x + (x
1
x
2
)y + x
1
(y
1
y
2
) + y
1
(x
2
x
1
) = 0
Ïîñëåäíåå óðàâíåíèå ïåðåïèøåì ñëåäóþùèì îáðàçîì:
ax + by + c = 0, (4)
ãäå a = y
2
y
1
,
b = x
1
x
2
,
c = x
1
(y
1
y
2
) + y
1
(x
2
x
1
).
Èòàê, âñÿêóþ ïðÿìóþ ìîæíî çàäàòü óðàâíåíèåì
âèäà (4). Â ñëåäóþùåì ïóíêòå ìû ïîêàæåì, ÷òî è íà-
îáîðîò, ïðè ëþáûõ çíà÷åíèÿõ êîýôôèöèåíòîâ (êðîìå
a = b = 0) óðàâíåíèå òàêîãî âèäà çàäàåò íà ïëîñêîñòè
íåêîòîðóþ ïðÿìóþ.
Çàìåòèì, ÷òî ïðè ïðîãðàììèðîâàíèè ïåðâóþ èç ôîð-
ìóë (3) íåëüçÿ èñïîëüçîâàòü â ôîðìå îòíîøåíèÿ
1
1
2
1
1
2
yy
yy
xx
xx
=
, òàê êàê, âî-ïåðâûõ, äàæå åñëè âñå
êîîðäèíàòû çàäàííûõ òî÷åê öåëûå, îøèáêè âåùåñòâåí-
íîé àðèôìåòèêè ïðè îïåðàöèè äåëåíèÿ íå ïîçâîëÿò
ïðîâåðÿòü ñ ïîìîùüþ óêàçàííîãî ñîîòíîøåíèÿ ïðèíàä-
ëåæíîñòü òîé èëè èíîé òî÷êè äàííîé ïðÿìîé, à, âî-
âòîðûõ, åñëè òî÷êà P ñîâïàäåò ñ P
1
, ïðîãðàììà áóäåò
ïðåðâàíà â ñèëó äåëåíèÿ íà íîëü.
Óðàâíåíèå ïðÿìîé ìîæíî çàïèñûâàòü è â ïàðàìåòðè-
÷åñêîì âèäå. Ëþáîé âåêòîð, ïðèëîæåííûé ê òî÷êå P
1
è
çàêàí÷èâàþùèéñÿ â ïðîèçâîëüíîé òî÷êå P(x, y), ëåæà-
ùåé íà íàøåé æå ïðÿìîé, ìîæíî ïîëó÷èòü èç
21
PP
ïó-
òåì óìíîæåíèÿ íà íåêîòîðîå âåùåñòâåííîå ÷èñëî t. Òîã-
äà äëÿ êàæäîé èç êîîðäèíàò â îòäåëüíîñòè ñïðàâåäëèâî:
(x x
1
) = t(x
2
x
1
) è (y y
1
) = t(y
2
y
1
).
Âûðàçèâ îòñþäà x è y, ïîëó÷àåì ñèñòåìó ïàðàìåòðè-
÷åñêèõ óðàâíåíèé, êîòîðîé óäîâëåòâîðÿåò êàæäàÿ òî÷êà
íàøåé ïðÿìîé:
x = x
1
+ t(x
2
x
1
),
y = y
1
+ t(y
2
y
1
). (5)
Íàîáîðîò, åñëè êîîðäèíàòû (x, y) òî÷êè P óäîâëåòâî-
ðÿþò ýòèì ñîîòíîøåíèÿì, âåêòîð
PP
1
êîëëèíåàðåí
21
PP
è, çíà÷èò, òî÷êà P ëåæèò íà ïðÿìîé P
1
P
2
. Òàêèì îáðà-
çîì, ñèñòåìà óðàâíåíèé (5), ãäå ïàðàìåòð t ïðîáåãàåò
âñþ äåéñòâèòåëüíóþ îñü, çàäàåò ïðÿìóþ P
1
P
2
.
Ýòà æå ñèñòåìà, íî ñî ââåäåííûìè îãðàíè÷åíèÿìè íà
çíà÷åíèÿ t, áóäåò çàäàâàòü è îòðåçîê P
1
P
2
, è ëó÷ P
1
P
2
. Äëÿ
îòðåçêà t ∈[0, 1] (òî åñòü x ìåíÿåòñÿ â äèàïàçîíå [x
1
, x
2
],
à y â äèàïàçîíå [y
1
, y
2
]), à äëÿ ëó÷à t ∈[0, ∞).
1.2. Óðàâíåíèå ïðÿìîé, çàäàííîé îäíîé èç åå òî÷åê è
âåêòîðîì íîðìàëè ê íåé.
Ïóñòü çàäàííàÿ òî÷êà P
0
ïðÿìîé èìååò êîîðäèíàòû
(x
0
, y
0
), à íåêîòîðûé âåêòîð íîðìàëè n ê íåé (òî åñòü
âåêòîð, îðòîãîíàëüíûé íàøåé ïðÿìîé) êîîðäèíàòû
(a, b). Åñëè P(x, y) ïðîèçâîëüíàÿ òî÷êà íà íàøåé ïðÿ-
ìîé, òî êîîðäèíàòû âåêòîðà
PP
0
ðàâíû (x x
0
, y y
0
).
Òîãäà ñêàëÿðíîå ïðîèçâåäåíèå îðòîãîíàëüíûõ âåêòîðîâ
(n,
PP
0
) ìîæíî âûðàçèòü òàê:
(n,
PP
0
) = a(x x
0
) + b(y y
0
) = 0. (6)
Î÷åâèäíî, ÷òî óðàâíåíèå ïðÿìîé (6) òàêæå íåñëîæíî
ïðèâåñòè ê âèäó (4). Òîãäà ñòàíîâèòñÿ ïîíÿòíî, ÷òî
êîýôôèöèåíòû a è b èç óðàâíåíèÿ (4) ïðåäñòàâëÿþò
ñîáîé êîîðäèíàòû îäíîãî èç âåêòîðîâ íîðìàëè ê îïè-
ñûâàåìîé äàííûì óðàâíåíèåì ïðÿìîé. Îòñþäà ñëåäó-
åò, ÷òî ïðè ëþáûõ çíà÷åíèÿõ êîýôôèöèåíòîâ a, b è c
(êðîìå a = b = 0) óðàâíåíèå (4) çàäàåò ïðÿìóþ. Åþ
áóäåò ïðÿìàÿ, ïåðïåíäèêóëÿðíàÿ âåêòîðó (a, b) è ïðî-
õîäÿùàÿ ÷åðåç òî÷êó, ÷üè êîîðäèíàòû óäîâëåòâîðÿþò (4).
Ïðè a ≠ 0 òàêîé òî÷êîé áóäåò, íàïðèìåð, òî÷êà
(
a
c
, 0), ïðè a = 0 òî÷êà (0,
b
c
).
Íåñìîòðÿ íà òî ÷òî ïîñòàíîâêà çàäà÷è íà ïåðâûé
âçãëÿä êàæåòñÿ íåñêîëüêî èñêóññòâåííîé, èìåííî ñ åå
ïîìîùüþ ìû ïîëó÷èëè óäîáíûé èíñòðóìåíò äëÿ ðàñ-
ñìîòðåíèÿ öåëîãî ðÿäà äðóãèõ çàäà÷.  ÷åì ñåé÷àñ íàì è
ïðåäñòîèò óáåäèòüñÿ.
1.3. Óðàâíåíèå ïðÿìîé, ïåðïåíäèêóëÿðíîé äàííîé è
ïðîõîäÿùåé ÷åðåç çàäàííóþ òî÷êó.
Ïóñòü çàäàííàÿ òî÷êà P
0
èñêîìîé ïðÿìîé èìååò êî-
îðäèíàòû (x
0
, y
0
). Åñëè P(x, y) ïðîèçâîëüíàÿ òî÷êà
íà òîé æå ïðÿìîé, òî êîîðäèíàòû âåêòîðà
PP
0
ðàâíû
(x x
0
, y y
0
). Ýòîò âåêòîð ïåðïåíäèêóëÿðåí âåêòîðó
21
PP
, ãäå P
1
(x
1
, y
1
) è P
2
(x
2
, y
2
) òî÷êè íà äàííîé
ïðÿìîé. Òîãäà ñêàëÿðíîå ïðîèçâåäåíèå îðòîãîíàëüíûõ
âåêòîðîâ (
21
PP
,
PP
0
) ìîæíî âûðàçèòü òàê:
(x
2
x
1
)(x x
0
) + (y
2
y
1
)(y y
0
) = 0 (7)
èëè
(x
2
x
1
)x + (y
2
y
1
)y + (x
2
x
1
)x
0
+ (y
2
y
1
)y
0
= 0.
Åñëè æå èñõîäíàÿ ïðÿìàÿ çàäàíà êîýôôèöèåíòàìè
a, b è c ñâîåãî óðàâíåíèÿ, òî ëåãêî çàìåòèòü, ÷òî âåê-
òîð åå íîðìàëè ñ êîîðäèíàòàìè (a, b) êîëëèíåàðåí
âåêòîðó
PP
0
.
2002 ¹ 39 ÈÍÔÎÐÌÀÒÈÊÀ
30
ÇÀÄÀ×È
Òîãäà, çàïèñûâàÿ êîñîå ïðîèçâåäåíèå ýòèõ âåêòîðîâ,
ïîëó÷èì
b(x x
0
) a(y y
0
) = 0. (8)
1.4. Óðàâíåíèå ïðÿìîé, ïàðàëëåëüíîé äàííîé è íàõî-
äÿùåéñÿ îò íåå íà çàäàííîì ðàññòîÿíèè r.
Î÷åâèäíî, ÷òî èñêîìûõ ïðÿìûõ äâå. Âåêòîð íîðìàëè ê
èñõîäíîé ïðÿìîé îðòîãîíàëåí è êàæäîé èç ïàðàëëåëüíûõ
ïðÿìûõ. Çíà÷èò, êîýôôèöèåíòû a è b ïðè x è y â óðàâíå-
íèè (4) äëÿ ïàðàëëåëüíûõ ïðÿìûõ ìîæíî âçÿòü òàêèìè
æå, êàê è ó èñõîäíîé ïðÿìîé. Îñòàåòñÿ ïîäîáðàòü çíà÷å-
íèå äëÿ òðåòüåãî èç êîýôôèöèåíòîâ. Îáîçíà÷èì åãî äëÿ
îäíîé ïðÿìîé c
1
, äëÿ âòîðîé c
2
. Êàê óæå áûëî ïîêàçà-
íî âûøå, äëÿ îïðåäåëåíèÿ ýòèõ êîýôôèöèåíòîâ äîñòàòî÷-
íî çíàòü õîòÿ áû ïî îäíîé òî÷êå íà êàæäîé ïðÿìîé.
Âîçüìåì ïðîèçâîëüíóþ òî÷êó P(x
0
, y
0
) íà èñõîäíîé ïðÿ-
ìîé (åñëè ïðÿìàÿ áûëà çàäàíà íå äâóìÿ òî÷êàìè, òî òî÷êó
ìîæíî íàéòè ïî ðåöåïòó, ïðåäëîæåííîìó â êîíöå 1.2).
Ïðîâåäåì ÷åðåç íåå ïðÿìóþ, ïåðïåíäèêóëÿðíóþ äàííîé.
Íà ïàðàëëåëüíîé æå ïðÿìîé áóäåì èñêàòü òî÷êó M(x
1
, y
1
)
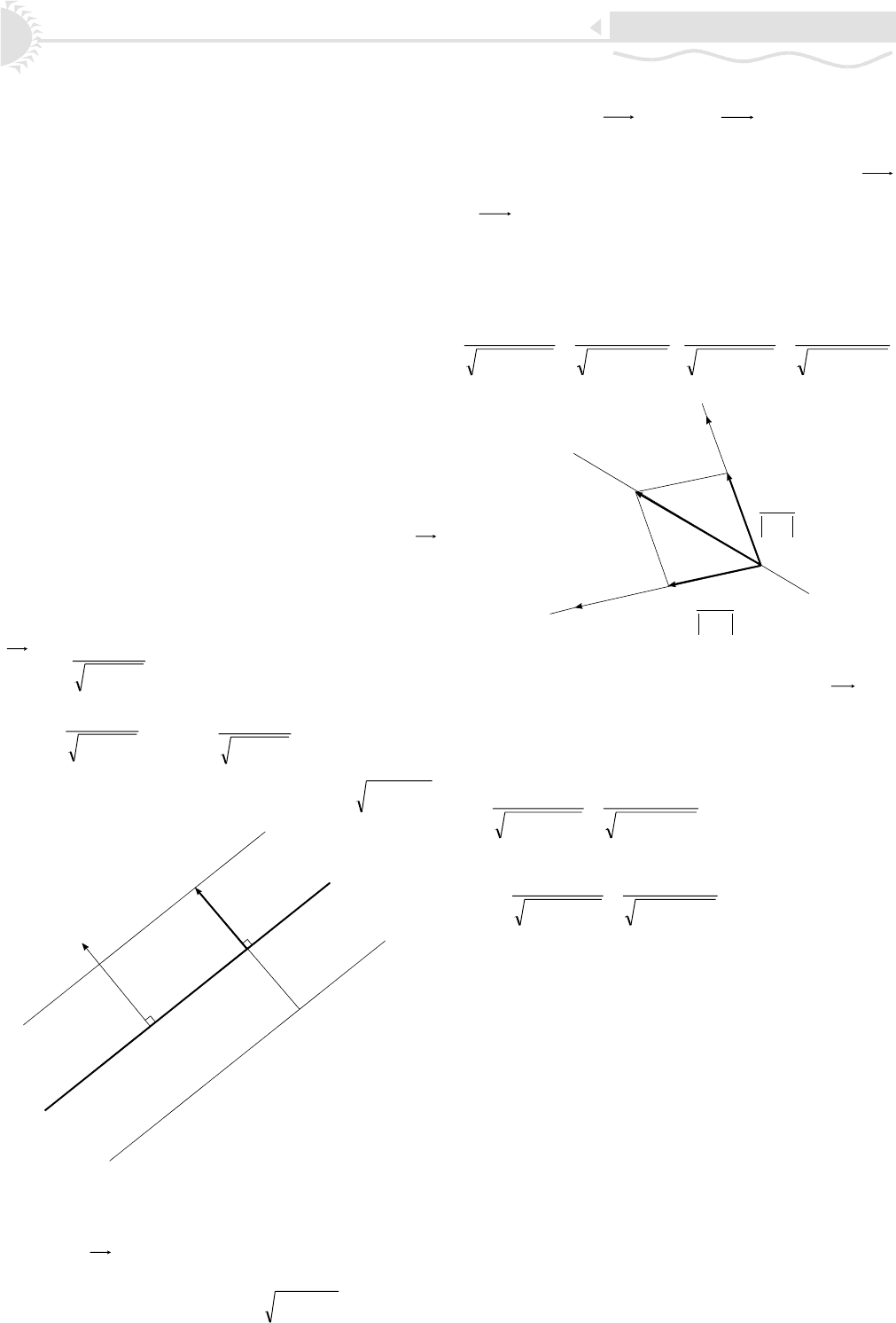
åå ïåðåñå÷åíèÿ ñ ýòèì ïåðïåíäèêóëÿðîì (ðèñ. 5). Íàì
èçâåñòåí îäèí âåêòîð íîðìàëè n = (a, b). Âåêòîð
PM
êîëëèíåàðåí åìó, à åãî äëèíà ðàâíà r. Äëÿ îïðåäåëåííî-
ñòè áóäåì ñ÷èòàòü, ÷òî, êàê è íà ðèñóíêå, íîðìàëü ëå-
æèò ïî òó æå ñòîðîíó îò ïðÿìîé, ÷òî è òî÷êà M. Òîãäà
22
ba
r
PM
+
⋅=
n
. Çíà÷èò, êîîðäèíàòû òî÷êè M ðàâíû
22
0
ba
r
ax
+
⋅+
,
22
0
ba
r
by
+
⋅+
. Ïîäñòàâëÿÿ èõ â
óðàâíåíèå (6), ïîëó÷àåì
2
2
00
1
barbyaxc
+=
.
n
r
P
M
Ðèñ. 5
Óðàâíåíèå îäíîé èç ïðÿìûõ ïîëó÷åíî.  êà÷åñòâå âåê-
òîðà íîðìàëè äëÿ äðóãîé ïðÿìîé ìîæíî èñïîëüçîâàòü
âåêòîð
PM
.  ýòîì ñëó÷àå èìååì
2
2
002
barbyaxc
++=
.
1.5. Óðàâíåíèå áèññåêòðèñû óãëà.
Ïóñòü âåêòîðû
10
PP
(x
1
, y
1
) è
20
PP
(x
2
, y
2
) ïðèëîæå-
íû ê òî÷êå P
0
(x
0
, y
0
). Íàéäåì óðàâíåíèå áèññåêòðèñû
óãëà P
1
P
0
P
2
. Åñëè ìû ðàçäåëèì êàæäûé èç âåêòîðîâ
10
PP
è
20
PP
íà åãî äëèíó, ïîëó÷èâ ïðè ýòîì âåêòîðû åäèíè÷-
íîé äëèíû, òî âåêòîð èõ ñóììû áóäåò ëåæàòü íà áèññåê-
òðèñå óãëà ìåæäó íèìè (ðèñ. 6). Êîîðäèíàòû ýòîãî âåê-
òîðà ðàâíû
2
2
2
2
2
2
1
2
1
1
yx
x
yx
x
+
+
+
,
2
2
2
2
2
2
1
2
1
1
yx
y
yx
y
+
+
+
.
P
2
P
0
P
1
Ðèñ. 6
Èç óñëîâèÿ åãî êîëëèíåàðíîñòè âåêòîðó
PP
0
, ãäå
P(x, y) ïðîèçâîëüíàÿ òî÷êà íà èñêîìîé ïðÿìîé, ïî-
ëó÷àåì óðàâíåíèå áèññåêòðèñû:
)(
2
2
2
2
2
2
1
2
1
1
0
+
+
+
xx
yx
y
yx
y
0)(
0
2
2
2
2
2
2
1
2
1
1
=
+
+
+
yy
yx
x
yx
x
.
(9)
Ïðè íåîáõîäèìîñòè èç (9) íåñëîæíî ïîëó÷èòü êîýô-
ôèöèåíòû a, b è c äëÿ çàïèñè óðàâíåíèÿ íàéäåííîé ïðÿ-
ìîé â âèäå (4).
1.6. Óðàâíåíèå îêðóæíîñòè.
Ïî îïðåäåëåíèþ îêðóæíîñòè ñ öåíòðîì â òî÷êå
M
0
(x
0
, y
0
) è ðàäèóñîì r, òî÷êà M(x, y) ïðèíàäëåæèò
åé òîãäà è òîëüêî òîãäà, êîãäà ðàññòîÿíèå ìåæäó M
0
è M
ðàâíî r. Çàïèñàâ ôîðìóëó äëÿ âû÷èñëåíèÿ êâàäðàòà ðàñ-
ñòîÿíèÿ ìåæäó äâóìÿ òî÷êàìè, ìû ïðèäåì ê ñëåäóþ-
ùåìó óðàâíåíèþ îêðóæíîñòè:
(x x
0
)
2
+ (y y
0
)
2
= r
2
. (10)
Íà ïðàêòèêå îêàçûâàåòñÿ ïîëåçíûì çíàíèå òàêæå è
ïàðàìåòðè÷åñêèõ óðàâíåíèé îêðóæíîñòè. Îáðàòèìñÿ
ñíà÷àëà ê îêðóæíîñòè ñ öåíòðîì â íà÷àëå êîîðäèíàò.
Åñëè îáîçíà÷èòü çà t óãîë ìåæäó ðàäèóñîì-âåêòîðîì
OM (çäåñü M(x, y) ïðîèçâîëüíàÿ òî÷êà îêðóæíîñòè)
02
02
PP
PP
KKKKH
0
1
0
1
PP
PP
KKK KH

2002 ¹ 39 ÈÍÔÎÐÌÀÒÈÊÀ
31
ÇÀÄÀ×È
è îñüþ Ox, îòñ÷èòûâàåìûé ïðîòèâ ÷àñîâîé ñòðåëêè, òî
î÷åâèäíî, ÷òî x = rcos t, y = rsin t. Çíà÷èò, äëÿ ïðîèç-
âîëüíîé îêðóæíîñòè ïàðàìåòðè÷åñêèå óðàâíåíèÿ áóäóò
âûãëÿäåòü òàê:
x = x
0
+ rcos t,
y = y
0
+ rsin t.
(11)
 çàêëþ÷åíèå ïîêàæåì, êàê îïðåäåëèòü äëèíó l íàè-
ìåíüøåé äóãè îêðóæíîñòè, åñëè èçâåñòíû êîîðäèíàòû
öåíòðà îêðóæíîñòè (x
0
, y
0
) è êîíöîâ äóãè (x
1
, y
1
) è
(x
2
, y
2
). Èç êóðñà ãåîìåòðèè èçâåñòíî, ÷òî äëèíà îê-
ðóæíîñòè ïðÿìî ïðîïîðöèîíàëüíà óãëó ϕ ìåæäó âåêòî-
ðàìè (x
1
x
0
, y
1
y
0
) è (x
2
x
0
, y
2
y
0
): l = rϕ. À
êàê âû÷èñëèòü çíà÷åíèå òàêîãî óãëà, óæå áûëî ïîêàçàíî
âûøå (íàäî òîëüêî ó÷åñòü, ÷òî â ñëó÷àå ïîèñêà äëèíû
íàèìåíüøåé èç äâóõ äóã íàñ èíòåðåñóåò íåîðèåíòèðî-
âàííûé óãîë â äèàïàçîíå [0, π]).
1.7. Êàñàòåëüíûå ê îêðóæíîñòè.
Ïóñòü îêðóæíîñòü èìååò öåíòð â òî÷êå P
0
(x
0
, y
0
) è
ðàäèóñ r. Òðåáóåòñÿ íàéòè óðàâíåíèå êàñàòåëüíûõ ê íåé,
ïðîõîäÿùèõ ÷åðåç òî÷êó P
1
(x
1
, y
1
). Çäåñü âîçìîæíû
òðè ñëó÷àÿ. Åñëè |P
0
P
1
| < r , òî P
1
ëåæèò âíóòðè îêðóæ-
íîñòè è êàñàòåëüíûõ, ïðîõîäÿùèõ ÷åðåç íåå, íå ñóùå-
ñòâóåò. Åñëè |P
0
P
1
| = r, òî P
1
ëåæèò íà îêðóæíîñòè.
Òîãäà ó èñêîìîé êàñàòåëüíîé íàì èçâåñòíû òî÷êà P
1
è
íîðìàëü
01
PP
, è åå óðàâíåíèå ëåãêî âûïèñûâàåòñÿ (ñì.
ï. 1.3). Íàêîíåö, â ñëó÷àå P
0
P
1
> r òî÷åê êàñàíèÿ äâå,
è, îáîçíà÷èâ îäíó èç íèõ P
2
, ìû èìååì ïðÿìîóãîëüíûé
òðåóãîëüíèê P
0
P
2
P
1
(ðèñ. 7). Ìîæíî ïîïûòàòüñÿ íàéòè
èñêîìîå óðàâíåíèå â ëîá. Åñëè (x
2
, y
2
) êîîðäèíà-
òû òî÷êè êàñàíèÿ P
2
, òî ïî òåîðåìå Ïèôàãîðà âûïèñû-
âàåòñÿ äëèíà îòðåçêà P
1
P
2
(P
0
P
2
= r, P
0
P
1
âû÷èñëÿåòñÿ
ïî èçâåñòíûì êîîðäèíàòàì). Äðóãîå ñîîòíîøåíèå íà
êîîðäèíàòû x
2
è y
2
óðàâíåíèå îêðóæíîñòè (10).
Îáà ýòè óðàâíåíèÿ êâàäðàòíûå. Ðåøåíèå òàêîé ñèñòå-
ìû óðàâíåíèé ïðåäñòàâëÿåò ñåðüåçíóþ òðóäíîñòü äëÿ
ó÷àùèõñÿ. Ïîïðîáóåì îáîéòèñü áåç êâàäðàòíûõ óðàâ-
íåíèé, èñïîëüçóÿ ñêàëÿðíîå è êîñîå ïðîèçâåäåíèÿ âåê-
òîðîâ.
P
0
P
2
P
3
P
1
r
Ðèñ. 7
Ìû áóäåì èñêàòü êîîðäèíàòû a = x
2
x
1
è b = y
2
y
1
âåêòîðà
21
PP
. Êàê óæå áûëî ñêàçàíî âûøå, äëèíû ñòîðîí
ïðÿìîóãîëüíîãî òðåóãîëüíèêà P
0
P
2
P
1
ëåãêî íàõîäÿòñÿ. Âû-
ïèøåì ñêàëÿðíîå ïðîèçâåäåíèå âåêòîðîâ
21
PP
è
01
PP
:
(
21
PP
,
01
PP
) = |P
1
P
2
| ⋅ |P
1
P
0
| ⋅ cos ϕ = |P
1
P
2
|
2
.
Ãåîìåòðè÷åñêèé ñìûñë êîñîãî ïðîèçâåäåíèÿ
[
01
PP
,
21
PP
] óäâîåííàÿ ïëîùàäü òðåóãîëüíèêà P
0
P
2
P
1
,
âçÿòàÿ ñî çíàêîì ïëþñ äëÿ îäíîé èç òî÷åê êàñàíèÿ è ñ
ìèíóñîì äëÿ äðóãîé:
[
01
PP
,
21
PP
] = ±|P
0
P
2
| ⋅ |P
1
P
2
|.
Çàïèñûâàÿ ýòè æå ïðîèçâåäåíèÿ â êîîðäèíàòàõ, ïîëó-
÷èì ñèñòåìó ëèíåéíûõ óðàâíåíèé îòíîñèòåëüíî a è b:
(x
0
x
1
) ⋅ a + (y
0
y
1
) ⋅ b = |P
1
P
2
|
2
,
(x
0
x
1
) ⋅ b (y
0
y
1
) ⋅ a = ±|P
0
P
2
| ⋅ |P
1
P
2
|.
Òàêóþ ñèñòåìó ðåøèòü óæå íåñëîæíî. Äàëåå ïî òî÷êå
P
1
(x
1
, y
1
) è íàïðàâëÿþùåìó âåêòîðó
21
PP
= (a, b) âû-
ïèñûâàåòñÿ óðàâíåíèå êàñàòåëüíîé. Çàäà÷à ðåøåíà. Åñëè
æå íàì òðåáóåòñÿ åùå íàéòè è êîîðäèíàòû òî÷êè êàñà-
íèÿ, òî ýòî ìîæíî ñäåëàòü, èñïîëüçóÿ êîîðäèíàòû òî÷êè
P
1
è íàéäåííûå êîîðäèíàòû âåêòîðà
21
PP
.
Ê ðåøåíèþ ýòîé æå çàäà÷è åñòü ïîäõîä, ïðè êîòîðîì
íå ïðèõîäèòñÿ ðåøàòü äàæå ñèñòåìó ëèíåéíûõ óðàâíå-
íèé. Îïóñòèì èç âåðøèíû P
2
ïðÿìîãî óãëà âûñîòó P
2
P
3
(ðèñ. 7). Èç ïîäîáèÿ òðåóãîëüíèêîâ P
1
P
2
P
0
è P
1
P
3
P
2
íàé-
äåì äëèíû îòðåçêîâ P
1
P
3
è P
3
P
2
:
1
0
2
2
1
3
1
PP
PP
PP
=
;
1
0
202
1
32
PP
PPPP
PP
⋅
=
. Òåïåðü ïîñëåäîâàòåëüíî íàõîäèì êî-
îðäèíàòû âåêòîðà
31
PP
, òî÷êè P
3
(x
3
, y
3
) è, íàêîíåö, èñïîëü-
çóÿ èçâåñòíûå êîîðäèíàòû âåêòîðà n = (y
0
y
1
, x
1
x
0
),
ïåðïåíäèêóëÿðíîãî ïðÿìîé P
1
P
3
, êîîðäèíàòû òî÷êè P
2
:
0
1
3
1
0
1
3
1
PP
PP
PPPP
⋅=
;
x
3
= x
1
+ (
31
PP
)
x
, y
3
= y
1
+ (
31
PP
)
y
;
n
n
23
23
PP
PP
⋅=
;
x
2
= x
3
+ (
23
PP
)
x
, y
2
= y
3
+ (
23
PP
)
y
.
Ïðîäîëæåíèå â ¹ 41/2002
2002 ¹ 40 ÈÍÔÎÐÌÀÒÈÊÀ
28
ÇÀÄÀ×È
H
P
2
P
1
h
P
Âû÷èñëèòåëüíàÿ ãåîìåòðèÿ íà ïëîñêîñòè
Å.Â. Àíäðååâà, Þ.Å. Åãîðîâ,
Ìîñêâà
Ïðîäîëæåíèå. Íà÷àëî â N¹ 39/2002
Âçàèìíîå ðàñïîëîæåíèå òî÷åê è ôèãóð
2.1. Ðàñïîëîæåíèå òî÷êè îòíîñèòåëüíî ïðÿìîé, ëó÷à
èëè îòðåçêà.
 ïåðâóþ î÷åðåäü â ýòîé çàäà÷å íàñ èíòåðåñóåò ïðè-
íàäëåæíîñòü äàííîé òî÷êè P(x, y) óêàçàííîìó ãåîìåò-
ðè÷åñêîìó îáúåêòó, óðàâíåíèå êîòîðîãî íàì èçâåñòíî
(ëèáî ìîæåò áûòü ëåãêî ïîëó÷åíî). ×òîáû îòâåòèòü
íà ýòîò âîïðîñ äëÿ ïðÿìîé, äîñòàòî÷íî ïîäñòàâèòü êî-
îðäèíàòû çàäàííîé òî÷êè â óðàâíåíèå ïðÿìîé (3) èëè
(4). Ðàâåíñòâî íóëþ çíà÷åíèÿ ïîëó÷åííîãî âûðàæåíèÿ
(äëÿ âåùåñòâåííûõ êîîðäèíàò èëè êîýôôèöèåíòîâ óðàâ-
íåíèÿ ïðîâåðêó íà ðàâåíñòâî íóëþ íåîáõîäèìî îñóùå-
ñòâëÿòü ñ ó÷åòîì ïîãðåøíîñòè) îçíà÷àåò, ÷òî òî÷êà ïðè-
íàäëåæèò äàííîé ïðÿìîé. Åñëè çíà÷åíèå âûðàæåíèÿ
ìåíüøå íóëÿ, òî òî÷êà ëåæèò â îäíîé ïîëóïëîñêîñòè îò
ïðÿìîé, åñëè áîëüøå íóëÿ â äðóãîé. Äåéñòâèòåëüíî,
óðàâíåíèå (3) ïîëó÷åíî â ïðåäïîëîæåíèè, ÷òî ïðÿìàÿ
ïðîõîäèò ÷åðåç òî÷êè P
1
(x
1
, y
1
) è P
2
(x
2
, y
2
). Çàìåòèì,
÷òî ëåâàÿ ÷àñòü (3) ýòî çíà÷åíèå êîñîãî ïðîèçâåäå-
íèÿ âåêòîðîâ
PP
1
è
2
1
PP
. Åãî çíàê îïðåäåëÿåò îðèåíòà-
öèþ ýòîé ïàðû âåêòîðîâ, èíà÷å ãîâîðÿ, ïðèíàäëåæíîñòü
òî÷êè P îäíîé èç ïîëóïëîñêîñòåé (à ðàâåíñòâî íóëþ
ïðèíàäëåæíîñòü ïðÿìîé).
Åñëè ïðÿìàÿ èçíà÷àëüíî çàäàíà äâóìÿ ñâîèìè òî÷êà-
ìè, òî äëÿ ðåøåíèÿ äàííîé çàäà÷è äîñòàòî÷íî âû÷èñ-
ëèòü çíà÷åíèå óêàçàííîãî êîñîãî ïðîèçâåäåíèÿ, à óðàâ-
íåíèå ïðÿìîé âûïèñûâàòü íå íóæíî.
 ñëó÷àå ïðîâåðêè ïðèíàäëåæíîñòè òî÷êè ëó÷ó ïðè
ðàâåíñòâå [
PP
1
,
2
1
PP
] íóëþ (çäåñü P
1
íà÷àëî ëó÷à, à
P
2
ëþáàÿ òî÷êà, ïðèíàäëåæàùàÿ ëó÷ó) ïîëåçíî âû-
÷èñëèòü è ñêàëÿðíîå ïðîèçâåäåíèå ýòèõ æå âåêòîðîâ.
Åñëè îíî ìåíüøå íóëÿ, òî P
1
ëåæèò íà ïðÿìîé ìåæäó P
2
è P, ñëåäîâàòåëüíî, P ëó÷ó íå ïðèíàäëåæèò. ×òîáû â àíà-
ëîãè÷íîé ñèòóàöèè óáåäèòüñÿ â ïðèíàäëåæíîñòè òî÷êè P
îòðåçêó P
1
P
2
, íåîáõîäèìî âû÷èñëèòü åùå è çíà÷åíèå ñêà-
ëÿðíîãî ïðîèçâåäåíèÿ
),(
2
1
2
PPPP
. Åñëè îíî íåîòðèöà-
òåëüíî, òî òî÷êà P ëåæèò íà îòðåçêå.
Ïóñòü òåïåðü íàì òðåáóåòñÿ îïðåäåëèòü, íà êàêîì
ðàññòîÿíèè íàõîäèòñÿ çàäàííàÿ òî÷êà P îò îïðåäåëåí-
íîé ïðÿìîé, ëó÷à èëè îòðåçêà. Ôîðìóëà äëÿ ðàññòîÿ-
íèÿ îò òî÷êè äî ïðÿìîé ïîëó÷àåòñÿ èç ñîïîñòàâëåíèÿ
äâóõ ñïîñîáîâ âû÷èñëåíèÿ ïëîùàäè òðåóãîëüíèêà:
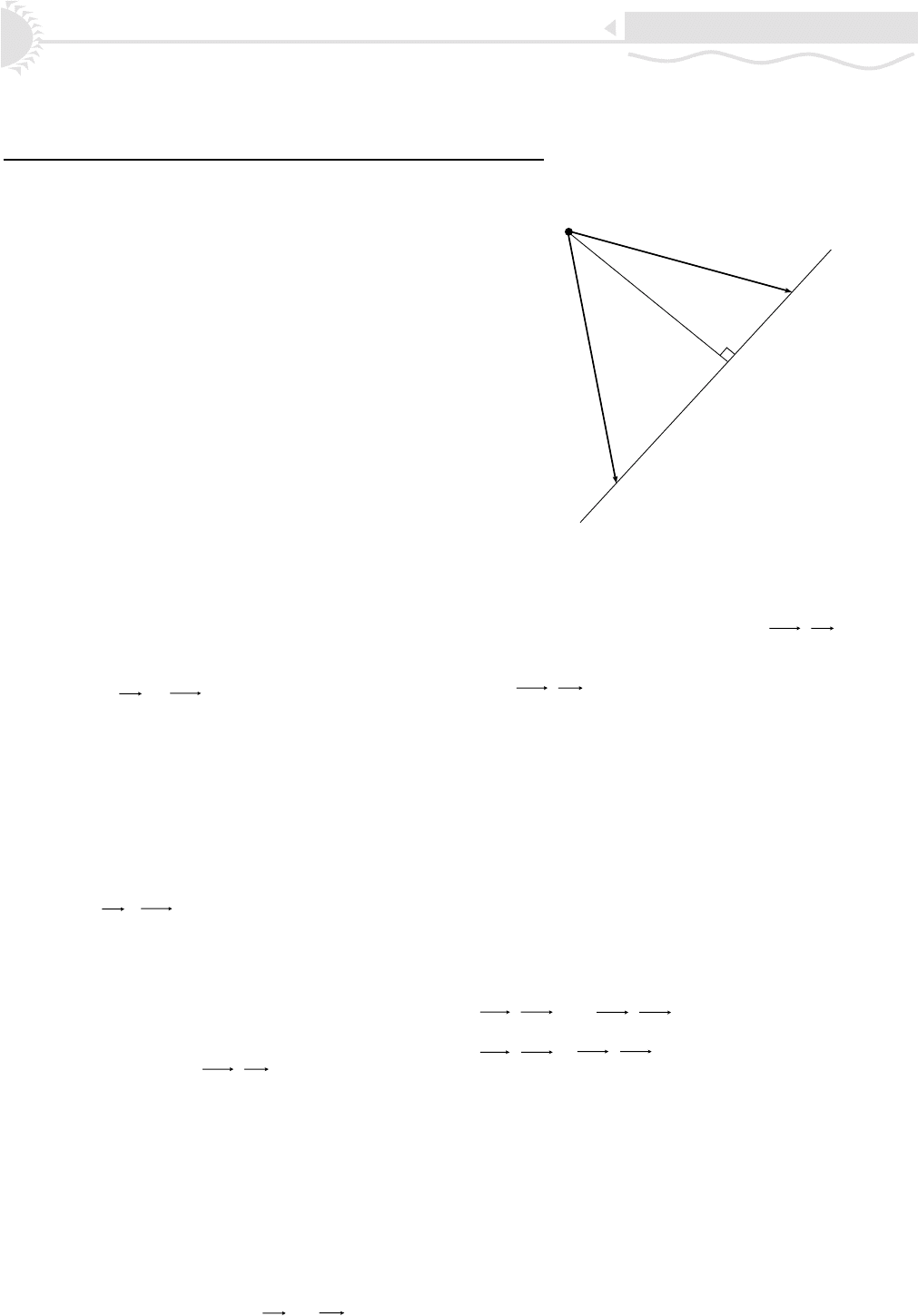
2S = h ⋅ |P
1
P
2
| = |[PP
1
, PP
2
]| (ñì. ðèñ. 8). Òî åñòü ðàññòî-
ÿíèå h îò òî÷êè P äî ïðÿìîé, çàäàííîé êîîðäèíàòàìè
òî÷åê P
1
è P
2
, ìîæíî ïîäñ÷èòàòü êàê îòíîøåíèå ìîäóëÿ
êîñîãî ïðîèçâåäåíèÿ âåêòîðîâ
1
PP
è
2
PP
ê äëèíå îò-
ðåçêà P
1
P
2
.
Äëÿ ëó÷à èëè îòðåçêà óêàçàííûé ñïîñîá íàõîæäåíèÿ
ðàññòîÿíèÿ íóæíî ñëåãêà ïîäêîððåêòèðîâàòü. Òî÷êà H
(ðèñ. 8) ïðèíàäëåæèò ëó÷ó P
1
P
2
â òîì è òîëüêî òîì ñëó-
÷àå, êîãäà ñêàëÿðíîå ïðîèçâåäåíèå
),(
1
2
1
PPPP
≥ 0. Äëÿ
îòðåçêà P
1
P
2
, êîíå÷íî, íóæíî åùå è âûïîëíåíèå óñëî-
âèÿ
),(
2
1
2
PPPP
≥ 0. Òîãäà ïðèìåíèìà ôîðìóëà ðàññòî-
ÿíèÿ îò òî÷êè äî ïðÿìîé.  ïðîòèâíîì ñëó÷àå ðàññòî-
ÿíèå îò òî÷êè äî ëó÷à (îòðåçêà) áóäåò ðàâíî ðàññòîÿ-
íèþ îò òî÷êè äî íà÷àëà ëó÷à (äî áëèæàéøåãî êîíöà
îòðåçêà).
2.2. Âçàèìíîå ðàñïîëîæåíèå äâóõ òî÷åê îòíîñèòåëüíî
ïðÿìîé.
Îáû÷íî òðåáóåòñÿ ïðîñòî âûÿñíèòü, ïî îäíó èëè ðàç-
íûå ñòîðîíû îò îïðåäåëåííîé ïðÿìîé ëåæàò äâå òî÷êè
P
1
è P
2
, çàäàííûå ñâîèìè êîîðäèíàòàìè. Âûáåðåì íà
ïðÿìîé äâå ïðîèçâîëüíûå íåñîâïàäàþùèå òî÷êè P
3
è
P
4
(èìè ìîãóò áûòü êàê ðàç òå òî÷êè, êîòîðûìè îïðåäå-
ëåíà íàøà ïðÿìàÿ). Òîãäà, åñëè êîñûå ïðîèçâåäåíèÿ
],[
4
3
1
3
PPPP
è
],[
4
323
PPPP
èìåþò ðàçíûé çíàê, òî åñòü
],[
4
3
1
3
PPPP
⋅
],[
4
323
PPPP
< 0, òî òî÷êè ëåæàò ïî ðàçíûå
ñòîðîíû îò ïðÿìîé; åñëè çíàêè ñîâïàäàþò òî ïî îäíó
ñòîðîíó, à åñëè îäíî èç íèõ ðàâíî 0, òî ñîîòâåòñòâóþùàÿ
òî÷êà ëåæèò íà èñõîäíîé ïðÿìîé. Âîîáùå æå ýòà çàäà÷à
ÿâëÿåòñÿ ÷àñòüþ ñëåäóþùåé, áîëåå ñëîæíîé, çàäà÷è.
2.3. Âçàèìíîå ðàñïîëîæåíèå äâóõ ïðÿìûõ èëè ïðÿ-
ìîé è îòðåçêà.
Ëåãêî âûÿñíèòü, ïåðåñåêàþòñÿ ëè äâå ïðÿìûå èëè ïà-
ðàëëåëüíû. Íàïîìíèì åùå ðàç, ÷òî óñëîâèå êîëëèíåàðíîñ-
òè äâóõ âåêòîðîâ ýòî ðàâåíñòâî íóëþ èõ êîñîãî ïðîèç-
âåäåíèÿ. Åñëè ïðÿìûå çàäàíû óðàâíåíèÿìè a
1
x + b
1
y +
+ c
1
= 0 è a
2
x + b
2
y + c
2
= 0, òî óäîáíî ïåðåéòè ê èõ
íîðìàëÿì n
1
= (a
1
, b
1
) è n
2
= (a
2
, b
2
). Òîãäà óñëîâèå
Ðèñ. 8
2002 ¹ 40 ÈÍÔÎÐÌÀÒÈÊÀ
29
ÇÀÄÀ×È
êîëëèíåàðíîñòè íîðìàëåé (à çíà÷èò, è ïàðàëëåëüíîñòè
ïðÿìûõ): [n
1
,
n
2
] = a
1
b
2
a
2
b
1
= 0. Åñëè ïðÿìûå çàäà-
íû ïàðàìè òî÷åê, òî òàêèì æå ñïîñîáîì ïðîâåðÿåòñÿ
êîëëèíåàðíîñòü íàïðàâëÿþùèõ âåêòîðîâ. Ïðîâåðêà íà-
ëè÷èÿ ïåðåñå÷åíèÿ ïðÿìîé è îòðåçêà íàìè ôàêòè÷åñêè
óæå áûëà ïðîèçâåäåíà ïðè ðåøåíèè çàäà÷è 2.2.
Ïóñòü ïðÿìàÿ è îòðåçîê ïåðåñåêàþòñÿ â îäíîé òî÷êå.
Íàéäåì åå.
Îáîçíà÷èì êîíöû îòðåçêà P
1
(x
1
, y
1
) è P
2
(x
2
, y
2
). Ïóñòü
P
3
(x
3
, y
3
) è P
4
(x
4
, y
4
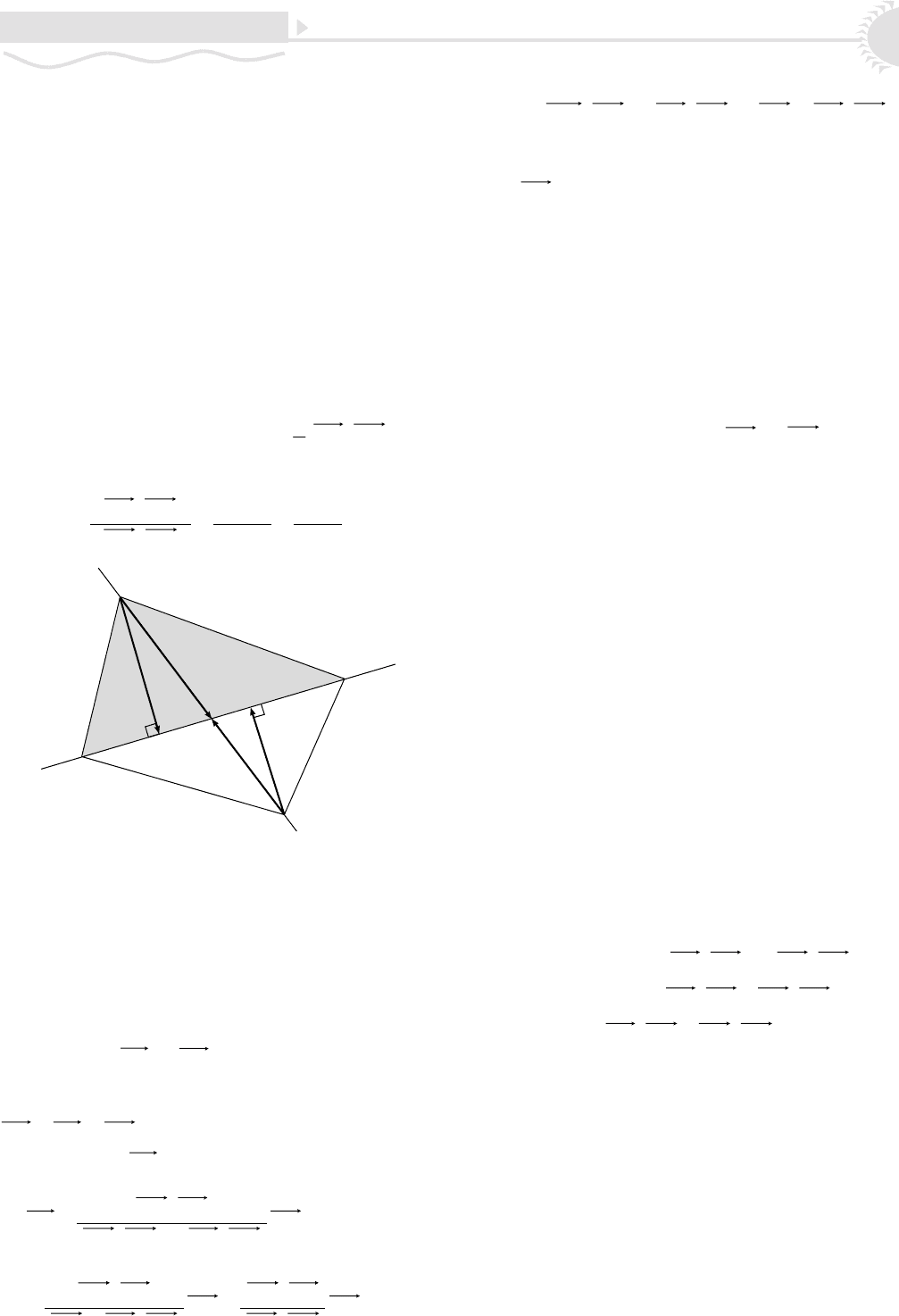
) äâå òî÷êè íà ïðÿìîé, à M
èñêîìàÿ òî÷êà ïåðåñå÷åíèÿ (ðèñ. 9). Îïóñòèì èç êîí-
öîâ îòðåçêà íà ïðÿìóþ ïåðïåíäèêóëÿðû P
1
H
1
è P
2
H
2
.
Òðåóãîëüíèêè P
3
P
1
P
4
è P
3
P
2
P
4
èìåþò îáùåå îñíîâàíèå.
Ñëåäîâàòåëüíî, îòíîøåíèå èõ ïëîùàäåé ðàâíî îòíîøå-
íèþ èõ âûñîò |P
1
H
1
| è |P
2
H
2
|. Íî ïëîùàäü (îðèåíòèðî-
âàííàÿ) òðåóãîëüíèêà P
3
P
1
P
4
ýòî
],[
2
1
4
3
1
3
PPPP
, àíà-
ëîãè÷íî âûðàæàåòñÿ ïëîùàäü P
3
P
2
P
4
. Òî åñòü
||
||
||
||
|],[|
|],[|
2
1
22
11
4
323
4
3
1
3
MP
MP
HP
HP
PPPP
PPPP
==
.
P
1
P
3
P
4
P
2
H
1
H
2
M
Ðèñ. 9
Ïîñëåäíåå ðàâåíñòâî âûòåêàåò èç ïîäîáèÿ òðåóãîëü-
íèêîâ P
1
H
1
M è P
2
H
2
M. Îòñþäà ïîëó÷àåì
32 3 3 3 2
41 1 4
[, ] [, ]
PP PP PM PP PP PM⋅= ⋅
KKKKHKKKKH KKKH KKKH KKKKHKKKKH
. (12)
 ýòîé ôîðìóëå ó÷òåíî è òî, ÷òî îäíà èç ïëîùàäåé
ìîæåò áûòü ðàâíà íóëþ, è òî, ÷òî óêàçàííûå ïëîùàäè
èìåþò îäèíàêîâûå çíàêè â òî÷íîñòè òîãäà, êîãäà òî÷êè
P
1
è P
2
ëåæàò ïî îäíó ñòîðîíó îò ïðÿìîé P
3
P
4
(òî åñòü
êîãäà âåêòîðû
MP
1
è
MP
2
ñîíàïðàâëåíû). Ìû íàøëè,
â êàêîì îòíîøåíèè äåëèòñÿ ýòîò îòðåçîê òî÷êîé M (âíóò-
ðåííèì èëè âíåøíèì îáðàçîì). Ñ äðóãîé ñòîðîíû,
2
11
2
PPMPMP
=
. Ïîäñòàâèì ýòî ñîîòíîøåíèå â (12).
Äàëåå âûðàçèòü
MP
1
äåëî òåõíèêè:
2
1
4
3
1
3
4
323
1
3
4
3
1
],[],[
],[
PP
PPPPPPPP
PPPP
MP
==
(13)
2
1
4
32
1
1
3
4
3
2
1
4
3
1
323
1
3
4
3
],[
],[
],[
],[
PP
PPPP
PPPP
PP
PPPPPP
PPPP
==
.
(Çäåñü ìû èñïîëüçîâàëè ñâîéñòâî ëèíåéíîñòè êîñîãî ïðî-
èçâåäåíèÿ:
],[],[],[
4
3
1
323
4
3
1
3
4
323
PPPPPPPPPPPPPP
=
,
êîòîðîå ëåãêî óñòàíàâëèâàåòñÿ, åñëè çàïèñàòü ýòî ðàâåíñò-
âî â êîîðäèíàòàõ.) Òåïåðü, çíàÿ êîîðäèíàòû òî÷êè P
1
è
âåêòîð
MP
1
, íàõîäèì òî÷êó M.
Òàêèì îáðàçîì, ìû íàøëè òî÷êó ïåðåñå÷åíèÿ ïðÿ-
ìîé è îòðåçêà. Äëÿ íàõîæäåíèÿ ïåðåñå÷åíèÿ äâóõ ïðÿ-
ìûõ íà îäíîé èç íèõ âûáèðàþòñÿ ïðîèçâîëüíûå òî÷êè
P
1
è P
2
, íà äðóãîé P
3
è P
4
.
Ìîæåò áûòü, âûâîä (13) íå ñîâñåì ýëåìåíòàðåí, íî
ñàìó ôîðìóëó ëåãêî çàïîìíèòü, åñëè ïîíÿòü åå ãåîìåò-
ðè÷åñêèé ñìûñë. Òàê, åñëè îòðåçêè P
1
P
2
è P
3
P
4
ïåðåñåêà-
þòñÿ, òî ïëîùàäü ÷åòûðåõóãîëüíèêà P
1
P
2
P
3
P
4
ïî èçâåñò-
íîé ôîðìóëå åñòü ïîëîâèíà ïðîèçâåäåíèÿ äèàãîíàëåé íà
ñèíóñ óãëà ìåæäó íèìè. Òî åñòü ïî àáñîëþòíîé âåëè÷è-
íå êîñîå ïðîèçâåäåíèå âåêòîðîâ
2
1
PP
è
4
3
PP
, ñòîÿùåå
â çíàìåíàòåëå ôîðìóëû (13), ýòî óäâîåííàÿ ïëîùàäü
÷åòûðåõóãîëüíèêà P
1
P
2
P
3
P
4
.  ÷èñëèòåëå æå ìû èìååì
óäâîåííóþ ïëîùàäü òðåóãîëüíèêà P
3
P
4
P
1
.
2.4. Îïðåäåëåíèå âçàèìíîãî ðàñïîëîæåíèÿ äâóõ îò-
ðåçêîâ èëè ëó÷åé.
Ïðîâåðèòü íàëè÷èå ïåðåñå÷åíèÿ ó äâóõ îòðåçêîâ (à
çà÷àñòóþ íàñ èíòåðåñóåò ëèøü ñàì ôàêò ïåðåñå÷åíèÿ)
íåñëîæíî îïÿòü æå ñ èñïîëüçîâàíèåì êîñîãî ïðîèçâåäå-
íèÿ. Ïóñòü ïåðâûé îòðåçîê çàäàí òî÷êàìè P
1
è P
2
, à
âòîðîé P
3
è P
4
. Îòðåçêè ïåðåñåêàþòñÿ òîãäà, êîãäà,
âî-ïåðâûõ, ïåðåñåêàþòñÿ îãðàíè÷èâàþùèå èõ ïðÿìî-
óãîëüíèêè è, âî-âòîðûõ, êîíöû êàæäîãî îòðåçêà ëåæàò
ïî ðàçíûå ñòîðîíû îò ïðÿìîé, êîòîðîé ïðèíàäëåæèò
äðóãîé îòðåçîê. Ïåðâîå èç ýòèõ óñëîâèé ïîçâîëÿåò íå
ðàññìàòðèâàòü îòäåëüíî òîò ñëó÷àé, êîãäà îòðåçêè ëåæàò
íà îäíîé ïðÿìîé.
Îáîçíà÷èì x
max1
è x
min1
ìàêñèìàëüíóþ è ìèíèìàëü-
íóþ èç x-êîîðäèíàò ïåðâîãî îòðåçêà, x
max2
è x
min2
âòî-
ðîãî îòðåçêà. Äëÿ y-êîîðäèíàò èìååì àíàëîãè÷íî y
max1
,
y
min1
, y
max2
è y
min2
. Òîãäà óñëîâèÿ ïåðåñå÷åíèÿ îòðåçêîâ
ôîðìàëüíî ìîæíî çàïèñàòü òàê:
1) x
max1
≥ x
min2
, x
max2
≥ x
min1
, y
max1
≥ y
min2
è y
max2
≥ y
min1
;
2) êîñûå ïðîèçâåäåíèÿ
],[
2
1
3
1
PPPP
è
],[
2
141
PPPP
èìå-
þò ðàçíûé çíàê, òî÷íåå,
0],[],[
2
141
2
1
3
1
≤⋅
PPPPPPPP
;
3) àíàëîãè÷íî
0],[],[
4
323
4
3
1
3
≤⋅
PPPPPPPP
.
Åñëè ôàêò íàëè÷èÿ ïåðåñå÷åíèÿ íàìè óæå óñòàíîâëåí,
òî äëÿ îòðåçêîâ, íàõîäÿùèõñÿ íà ïåðåñåêàþùèõñÿ ïðÿ-
ìûõ, òî÷êà ïåðåñå÷åíèÿ èùåòñÿ, êàê è â çàäà÷å 2.3. Äëÿ
îòðåçêîâ îäíîé ïðÿìîé èõ ïåðåñå÷åíèå (òî÷êó èëè îò-
ðåçîê) ìîæíî íàéòè ïóòåì ïîäñ÷åòà çíà÷åíèÿ äâóõ ñêà-
ëÿðíûõ ïðîèçâåäåíèé àíàëîãè÷íî çàäà÷å 2.1 èëè ñ ïîìî-
ùüþ ñðàâíåíèÿ êîîðäèíàò êîíöîâ îòðåçêîâ.
Ââåäåì òåïåðü ïîíÿòèå ðàññòîÿíèÿ ìåæäó äâóìÿ íå-
ïåðåñåêàþùèìèñÿ îòðåçêàìè êàê ìèíèìàëüíîå ñðåäè
ðàññòîÿíèé ìåæäó âñåìè ïàðàìè òî÷åê äâóõ îòðåçêîâ.
Íåñëîæíî ïîíÿòü, ÷òî îíî ðàâíî ðàññòîÿíèþ îò êîíöà
îäíîãî èç îòðåçêîâ äî äðóãîãî îòðåçêà (çàäà÷à 2.1).
Ïîýòîìó äëÿ ðåøåíèÿ çàäà÷è äîñòàòî÷íî ïîäñ÷èòàòü
2002 ¹ 40 ÈÍÔÎÐÌÀÒÈÊÀ
30
ÇÀÄÀ×È
ñîîòâåòñòâóþùåå ðàññòîÿíèå äëÿ êàæäîé èç ÷åòûðåõ êîí-
öåâûõ òî÷åê è âûáðàòü èç íèõ ìèíèìàëüíîå.
Äëÿ ïðîâåðêè íàëè÷èÿ ïåðåñå÷åíèÿ äâóõ ëó÷åé P
1
P
2
è
P
3
P
4
ñëåäóåò èçó÷èòü âçàèìíîå ðàñïîëîæåíèå ñîîòâåòñòâó-
þùèõ ïðÿìûõ. Ðàâåíñòâî íóëþ êîñîãî ïðîèçâåäåíèÿ
],[
4
32
1
PPPP
îçíà÷àåò ïðèíàäëåæíîñòü ëó÷åé ïàðàëëåëü-
íûì ïðÿìûì. Åñëè ýòè ïðÿìûå ðàçëè÷íû, òî âåêòîðû
3
1
PP
è
2
1
PP
íåêîëëèíåàðíû è, çíà÷èò, êîñîå ïðîèçâåäå-
íèå
],[
2
1
3
1
PPPP
îòëè÷íî îò íóëÿ.  ýòîì ñëó÷àå ëó÷è íå
ïåðåñåêàþòñÿ. Êîãäà ëó÷è ëåæàò íà îäíîé ïðÿìîé, ñ
ïîìîùüþ çíàêà ñêàëÿðíîãî ïðîèçâåäåíèÿ
),(
4
32
1
PPPP
ìîæíî ïîíÿòü, â îäíó èëè â ðàçíûå ñòîðîíû îíè íàïðàâ-
ëåíû.  ïåðâîì ñëó÷àå ñêàëÿðíîå ïðîèçâåäåíèå áóäåò ïî-
ëîæèòåëüíûì, à âî âòîðîì îòðèöàòåëüíûì. Åñëè ëó÷è
ñîíàïðàâëåíû, òî îïðåäåëèòü, êàêîé èç ëó÷åé ÿâëÿåòñÿ èõ
ïåðåñå÷åíèåì, ìîæíî, ïîäñ÷èòàâ çíà÷åíèå ñêàëÿðíîãî ïðî-
èçâåäåíèÿ
),(
3
1
2
1
PPPP
. Êîãäà îíî áîëüøå íóëÿ, ïåðåñå÷å-
íèåì ÿâëÿåòñÿ ëó÷ P
3
P
4
, â ïðîòèâíîì ñëó÷àå ëó÷ P
1
P
2
. Â
ñëó÷àå æå ïðîòèâîïîëîæíîé íàïðàâëåííîñòè ëó÷åé èõ ïå-
ðåñå÷åíèå ëèáî îòðåçîê P
1
P
3
, è òîãäà íà÷àëî ëþáîãî èç
äâóõ ëó÷åé ëåæèò âíóòðè äðóãîãî ëó÷à:
0),(
3
1
2
1
>
PPPP
,
ëèáî îäíà òî÷êà P
1
= P
3
:
0),(
3
1
2
1
=
PPPP
, ëèáî îíî ïóñ-
òî:
0),(
3
1
2
1
<
PPPP
.
Íàêîíåö, åñëè ïðÿìûå P
1
P
2
è P
3
P
4
ïåðåñåêàþòñÿ â îä-
íîé òî÷êå M
)0],([
4
32
1
≠
PPPP
, òî íàéòè ýòó òî÷êó ìîæ-
íî òàê æå, êàê â çàäà÷å 2.3. Çàòåì ñëåäóåò ïðîâåðèòü,
÷òî M ïðèíàäëåæèò êàæäîìó èç ëó÷åé:
0),(
1
2
1
≥
MPPP
è
0),(
3
4
3
≥
MPPP
.
2.5. Âçàèìíîå ðàñïîëîæåíèå îêðóæíîñòè è ïðÿìîé.
Ïðÿìàÿ ìîæåò ïåðåñåêàòü îêðóæíîñòü â äâóõ òî÷êàõ,
êàñàòüñÿ åå èëè íå èìåòü ñ îêðóæíîñòüþ îáùèõ òî÷åê.
Ýòè ñëó÷àè ëåãêî îïðåäåëÿþòñÿ. Äîñòàòî÷íî íàéòè ðàñ-
ñòîÿíèå îò öåíòðà îêðóæíîñòè äî äàííîé ïðÿìîé (ïî
ôîðìóëå ðàññòîÿíèÿ îò òî÷êè äî ïðÿìîé, ñì. 2.1). Åñëè
ýòî ðàññòîÿíèå (îáîçíà÷èì åãî l) ìåíüøå ðàäèóñà îê-
ðóæíîñòè r, òî ïðÿìàÿ ïåðåñåêàåò îêðóæíîñòü â äâóõ
òî÷êàõ, åñëè ðàâíî åìó, òî ïðÿìàÿ êàñàåòñÿ îêðóæíîñ-
òè, à åñëè îíî áîëüøå ðàäèóñà, òî îáùèõ òî÷åê íåò. Â
ïîñëåäíåì ñëó÷àå íàñ ìîæåò èíòåðåñîâàòü è ðàññòîÿíèå
îò ïðÿìîé äî îêðóæíîñòè. Îíî ðàâíî l r.
Áîëåå ñëîæíîé ÿâëÿåòñÿ çàäà÷à ïîèñêà îáùèõ òî÷åê ïðÿ-
ìîé è îêðóæíîñòè. Ñëó÷àé êàñàíèÿ áûë ðàññìîòðåí íàìè â
ï. 1.7. Ïóñòü òåïåðü ïðÿìàÿ è îêðóæíîñòü ïåðåñåêàþòñÿ â
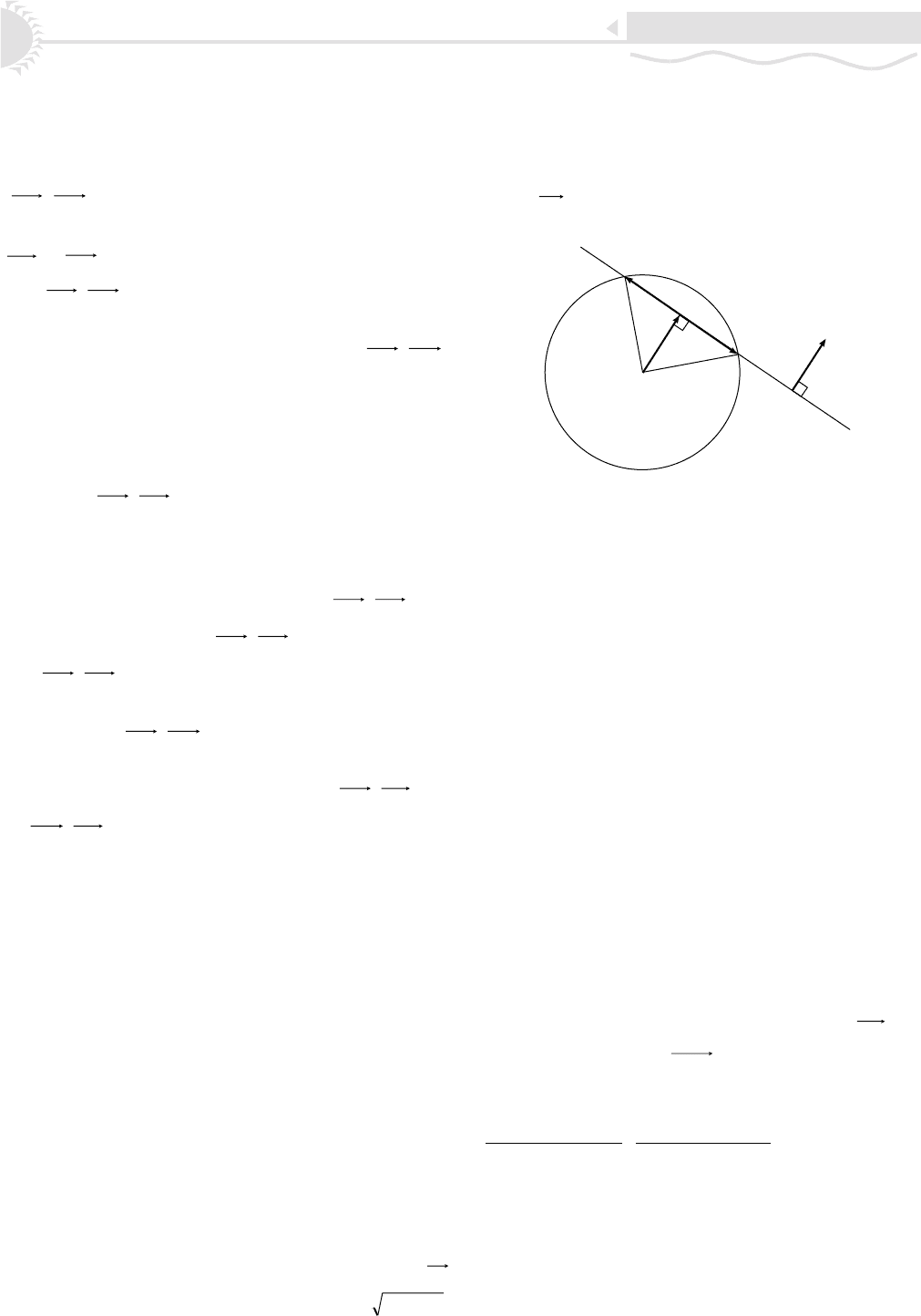
äâóõ òî÷êàõ. Êîîðäèíàòû ýòèõ òî÷åê ìîæíî íàéòè ïî ñëåäó-
þùåìó àëãîðèòìó (ðèñ. 10). Íàéäåì âåêòîð n íîðìàëè ê
ïðÿìîé. Îòëîæèì â íàïðàâëåíèè ýòîãî âåêòîðà âåêòîð
OA
äëèíû l. Âû÷èñëèì ðàññòîÿíèå |AP
1
| = |AP
2
| =
22
lr
.
Îò òî÷êè A âäîëü ïðÿìîé îòëîæèì â îáå ñòîðîíû âåê-
òîðû äëèíû |AP
1
|. Èõ êîíöû äàäóò íàì äâå èñêîìûå
òî÷êè P
1
è P
2
. Êàæäûé èç øàãîâ ýòîãî àëãîðèòìà â
îòäåëüíîñòè íàìè óæå ðàññìàòðèâàëñÿ ðàíåå. Çàìåòèì òîëü-
êî, ÷òî íà ïåðâîì øàãå íåîáõîäèìî ïðàâèëüíî âûáðàòü
îäíî èç äâóõ âîçìîæíûõ íàïðàâëåíèé íîðìàëè ê ïðÿìîé.
Äëÿ ýòîãî äîñòàòî÷íî ïðîâåðèòü, ÷òî ñêàëÿðíîå ïðîèçâåäå-
íèå
0),(
≥
OMn
, ãäå M ïðîèçâîëüíàÿ òî÷êà ïðÿìîé.
r
l
A
P
1
P
2
O
n
Ðèñ. 10
2.6. Âçàèìíîå ðàñïîëîæåíèå äâóõ îêðóæíîñòåé.
Äâå ðàçëè÷íûå îêðóæíîñòè òàêæå ìîãóò ïåðåñåêàòü-
ñÿ â äâóõ òî÷êàõ, êàñàòüñÿ äðóã äðóãà èëè íå èìåòü îá-
ùèõ òî÷åê.  ïîñëåäíåì ñëó÷àå îäíà èç îêðóæíîñòåé
ìîæåò ðàñïîëàãàòüñÿ âíóòðè äðóãîé (íàçîâåì òàêèå îê-
ðóæíîñòè âëîæåííûìè) èëè êàæäàÿ èç îêðóæíîñòåé
ëåæèò âíå äðóãîé.
Ïðîâåðêà íàëè÷èÿ ïåðåñå÷åíèÿ èëè êàñàíèÿ àíàëî-
ãè÷íî ïðåäûäóùåé çàäà÷å îñóùåñòâëÿåòñÿ ïóòåì ñðàâ-
íåíèÿ ðàññòîÿíèÿ ìåæäó öåíòðàìè îêðóæíîñòåé (îáî-
çíà÷èì åãî l) ñ èõ ðàäèóñàìè. Åñëè l > r
1
+ r
2
èëè
l < |r
1
r
2
|, òî îêðóæíîñòè îáùèõ òî÷åê íå èìåþò.
Âòîðîå óñëîâèå îáîçíà÷àåò âëîæåííîñòü îäíîé îêðóæ-
íîñòè â äðóãóþ. Ïðè çàìåíå çíàêà ëþáîãî èç ýòèõ
äâóõ íåðàâåíñòâ íà ðàâåíñòâî ìû ïîëó÷èì ñëó÷àé êà-
ñàíèÿ îêðóæíîñòåé (âíåøíåãî èëè âíóòðåííåãî). Åñëè
æå |r
1
r
2
| < l < r
1
+ r
2
, òî îêðóæíîñòè èìåþò ðîâíî
äâå òî÷êè ïåðåñå÷åíèÿ.
Êîîðäèíàòû òî÷êè êàñàíèÿ îêðóæíîñòåé íàéòè î÷åíü
ïðîñòî. Âåäü öåíòðû îêðóæíîñòåé O
1
(x
1
, y
1
) è O
2
(x
2
, y
2
)
çàäàþò ïðÿìóþ, íà êîòîðîé ëåæèò è òî÷êà êàñàíèÿ
P(x
3
, y
3
). Áóäåì ñ÷èòàòü, ÷òî òî÷êà O
1
ÿâëÿåòñÿ öåíòðîì
îêðóæíîñòè áîëüøåãî ðàäèóñà. Òîãäà âåêòîð
PO
1
ñî-
íàïðàâëåí ñ âåêòîðîì
2
1
OO
. Äëèíû îáîèõ âåêòîðîâ
òàêæå èçâåñòíû, ïîýòîìó èñêîìûå êîîðäèíàòû ðàâíû
++
l
ryyy
l
rxxx
11
2
111
2
1
)(
,
)(
. Ïðîâåðüòå, ÷òî
åñëè r
1
< r
2
, òî â ñëó÷àå âëîæåííîñòè îêðóæíîñòåé ïîëó-
÷åííàÿ ôîðìóëà íóæäàåòñÿ â êîððåêòèðîâêå.
Ïðè ïîèñêå êîîðäèíàò äâóõ òî÷åê ïåðåñå÷åíèÿ îê-
ðóæíîñòåé âîñïîëüçóåìñÿ ìåõàíèçìîì, óæå îïèñàííûì
â çàäà÷å 1.7. Ðàññìîòðèì òðåóãîëüíèê O
1
O
2
P (ðèñ. 11). Â
íåì íàì èçâåñòíû äëèíû âñåõ òðåõ ñòîðîí (r
1
> r
2
è l).
Ïðîâåäåì â òðåóãîëüíèêå âûñîòó PH.  ïîëó÷èâøåìñÿ
ïðÿìîóãîëüíîì òðåóãîëüíèêå O
1
HP íåèçâåñòíû äëèíû
êàòåòîâ. Íàéäåì O
1
H, çàïèñàâ òåîðåìó êîñèíóñîâ äëÿ
2002 ¹ 40 ÈÍÔÎÐÌÀÒÈÊÀ
31
ÇÀÄÀ×È
òðåóãîëüíèêà O
1
O
2
P: r
2
2
= r
1
2
+ l
2
2lr
1
⋅
cos ϕ =
= r
1
2
+ l
2
2l ⋅ |O
1
H|. Îòñþäà
l
rlr
HO
2
)(
||
2
2
2
2
1
1
+
=
.
Ïî òåîðåìå Ïèôàãîðà |HP | =
2
1
2
1
||
OHr
. Òåïåðü
ïîñëåäîâàòåëüíî íàõîäèì: âåêòîð
1
2
11
||
OH
OH OO
l
=
KKKKH KKKKKH
,
òî÷êó Í ïî èçâåñòíîé òî÷êå O
1
è âåêòîðó
HO
1
, âåêòîð
n = (y
2
y
1
, x
1
x
2
), ïåðïåíäèêóëÿðíûé O
1
O
2
, âåêòîð
n
n ||
|| HP
HP
=
, íàêîíåö, òî÷êó P ïî èçâåñòíîé òî÷êå H è
âåêòîðó
HP
. Çàìåíèâ â ïîñëåäíåì äåéñòâèè âåêòîð
HP
íà ïðîòèâîïîëîæíûé, ïîëó÷èì è âòîðóþ òî÷êó ïåðåñå-
÷åíèÿ îêðóæíîñòåé.
O
1
O
2
P
H
r
2
r
1
Ðèñ. 11
Çàìåòèì, ÷òî ïðè ðåøåíèè çàäà÷ 1.7, 2.5 è 2.6 ìû
èñïîëüçóåì ïîøàãîâûå àëãîðèòìû. À èìåííî, àíàëèçè-
ðóÿ ÷åðòåæ, âûäåëÿåì öåïî÷êó îáúåêòîâ (âåêòîðîâ, òî÷åê
è ò.ï.), êàæäûé èç êîòîðûõ çà îäèí ýëåìåíòàðíûé øàã
ïîëó÷àåòñÿ èç óæå íàéäåííûõ îáúåêòîâ. Ôàêòè÷åñêè ìû
ïîñëåäîâàòåëüíî âîññòàíàâëèâàåì ïàðàìåòðû îáúåêòîâ,
âûäåëåííûõ íàìè íà ÷åðòåæå. Öåïî÷êà âû÷èñëåíèé äîë-
æíà ïðèâåñòè íàñ ê îòâåòó, ïðè ýòîì êàæäûé øàã ïðå-
äåëüíî ïðîñò è âïîëíå î÷åâèäåí. Íå èñêëþ÷åíî, ÷òî ó
çàäà÷è èìååòñÿ áîëåå êîðîòêîå àíàëèòè÷åñêîå ðåøåíèå
(íàïðèìåð, ðåøåíèå ñèñòåìû óðàâíåíèé). Îäíàêî ïî-
øàãîâûé ìåòîä â ñèëó ñâîåé íàãëÿäíîñòè ïðîçðà÷åí è
ïîçâîëÿåò êîíòðîëèðîâàòü êàæäûé øàã ðåøåíèÿ, à èìåí-
íî ýòî êà÷åñòâî ìîæåò ñûãðàòü ðåøàþùóþ ðîëü ïðè ïðî-
âåðêå àëãîðèòìà è îòëàäêå ïðîãðàììû.
2.7. Ïðîâåðêà ïðèíàäëåæíîñòè òî÷êè âíóòðåííåé
îáëàñòè ìíîãîóãîëüíèêà.
Ïóñòü M íåêîòîðàÿ òî÷êà ïëîñêîñòè. Òðåáóåòñÿ
îïðåäåëèòü åå ìåñòîíàõîæäåíèå îòíîñèòåëüíî çàìêíó-
òîé ëîìàíîé, ÿâëÿþùåéñÿ ãðàíèöåé ìíîãîóãîëüíèêà.
Ðàññìîòðèì ñíà÷àëà ñëó÷àé âûïóêëîãî ìíîãîóãîëüíèêà.
Ïóñòü çàäàííûå ñâîèìè êîîðäèíàòàìè âåðøèíû ìíîãî-
óãîëüíèêà P
0
, P
1
, , P
n1
ïåðå÷èñëåíû â ïîðÿäêå åãî îá-
õîäà ïðîòèâ ÷àñîâîé ñòðåëêè. Ïðè òàêîì îáõîäå ìíîãî-
óãîëüíèê ëåæèò ñëåâà îò ãðàíèöû. È, çíà÷èò, åñëè òî÷êà
M ëåæèò âíóòðè ìíîãîóãîëüíèêà, òî îðèåíòèðîâàííûé
óãîë ìåæäó âåêòîðàìè
MP
i
è
1
+
i
i
PP
îòðèöàòåëåí. Ïî-
ýòîìó íàì äîñòàòî÷íî ïîäñ÷èòàòü âåëè÷èíó êîñûõ ïðî-
èçâåäåíèé
1
[, ]
ii
i
PM PP
+
KKKH KKKKKH
, i = 0, 1, , n 1; çíà÷åíèå
i + 1 áåðåòñÿ ïî ìîäóëþ n. Åñëè âñå ïîëó÷åííûå ïðè
ýòîì çíà÷åíèÿ îòðèöàòåëüíû, òî òî÷êà M âíóòðåííÿÿ.
Åñëè æå îäíî èç íèõ ðàâíî íóëþ, à âñå îñòàëüíûå îòðè-
öàòåëüíû, òî M ïðèíàäëåæèò ãðàíèöå ìíîãîóãîëüíèêà
(óáåäèòåñü, ÷òî ïðîñòî ðàâåíñòâà íóëþ îäíîãî èç çíà÷å-
íèé íå äîñòàòî÷íî).  ïðîòèâíîì æå ñëó÷àå òî÷êà M
ëåæèò âíå íàøåãî ìíîãîóãîëüíèêà.
Ðàññìîòðèì òåïåðü ïðîèçâîëüíûé ìíîãîóãîëüíèê.
Ïðîâåäåì ãîðèçîíòàëüíûé ëó÷ èç òî÷êè M, íàïðèìåð,
âëåâî. Òàê êàê ìíîãîóãîëüíèê îãðàíè÷åí, òî âñåãäà ëåãêî
óêàçàòü íà ýòîì ëó÷å òî÷êó P(x, y), çàâåäîìî åìó íå
ïðèíàäëåæàùóþ. Äàëåå ïîäñ÷èòàåì êîëè÷åñòâî ïåðåñå-
÷åíèé îòðåçêà PM ñ ãðàíèöåé ìíîãîóãîëüíèêà. Åñëè îíî
ðàâíî íóëþ èëè ÷åòíî, òî òî÷êà M ëåæèò âíå ìíîãî-
óãîëüíèêà, â ïðîòèâíîì ñëó÷àå âíóòðè íåãî.
Êîëè÷åñòâî ïåðåñå÷åíèé îòðåçêà PM ñ ãðàíèöåé ìû
ïîäñ÷èòàåì, ðàññìîòðåâ ïî î÷åðåäè ïåðåñå÷åíèå îòðåçêà
PM ñ êàæäûì èç çâåíüåâ ëîìàíîé. Ïðè ýòîì âîçìîæíû
ñëåäóþùèå îñîáûå ñëó÷àè.
1. Îäíî èç çâåíüåâ ëîìàíîé öåëèêîì ñîäåðæèòñÿ âíóò-
ðè îòðåçêà PM.
2. Çâåíî ëîìàíîé êàñàåòñÿ îòðåçêà PM.
3. M ëåæèò íà îäíîì èç çâåíüåâ ëîìàíîé.
 ïîñëåäíåì ñëó÷àå M ïðèíàäëåæèò ãðàíèöå ìíîãî-
óãîëüíèêà, è â ïîäñ÷åòå îáùåãî ÷èñëà ïåðåñå÷åíèé íåîá-
õîäèìîñòè íåò. Äëÿ äâóõ ïåðâûõ ñëó÷àåâ ïîñòóïèì ñëå-
äóþùèì îáðàçîì.  ïåðâîì ñëó÷àå ïåðåñå÷åíèå áóäåì
èãíîðèðîâàòü. Âî âòîðîì äîïîëíèòåëüíî ïðîâåðèì,
íèæíèì èëè âåðõíèì êîíöîì çâåíî ëîìàíîé êàñà-
åòñÿ ãîðèçîíòàëüíîãî îòðåçêà PM. Åñëè òî÷êîé êàñàíèÿ
ÿâëÿåòñÿ íèæíèé êîíåö çâåíà, òî ïåðåñå÷åíèå èãíî-
ðèðóåòñÿ, à åñëè âåðõíèé òî çàñ÷èòûâàåòñÿ. Ñ ó÷å-
òîì ýòîãî ñîãëàøåíèÿ êàñàíèå îòðåçêà PM ãðàíèöû ìíî-
ãîóãîëüíèêà â îäíèõ òî÷êàõ èãíîðèðóåòñÿ, à â äðóãèõ
òî÷êàõ ñ÷èòàåòñÿ äâàæäû. Ýòî íå èçìåíèò ÷åòíîñòè ÷èñ-
ëà ïåðåñå÷åíèé, à òîëüêî îíà âàæíà ïðè ïîèñêå îòâåòà
íà âîïðîñ äàííîé çàäà÷è. Åñëè æå îòðåçîê äåéñòâèòåëü-
íî ïåðåñåêàåò ëîìàíóþ â åå âåðøèíå, òî, ïî íàøåìó
ñîãëàøåíèþ, ÷èñëî ïåðåñå÷åíèé êàê ðàç óâåëè÷èòñÿ íà
åäèíèöó (ïåðåñå÷åíèå ñ âåðõíèì ðåáðîì çàñ÷èòàíî íå
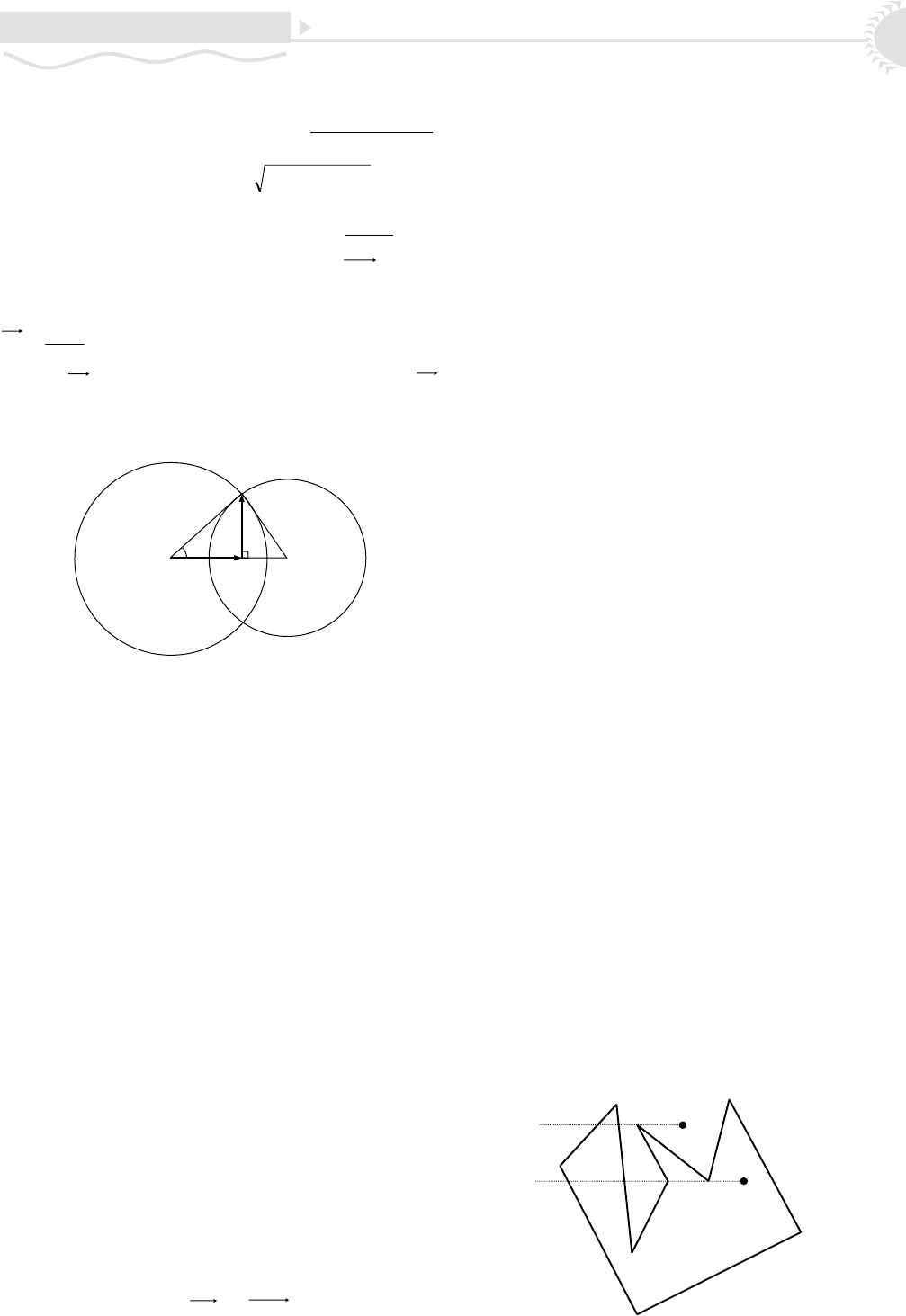
áóäåò, à ñ íèæíèì áóäåò). Íàïðèìåð, íà ðèñ. 12
êîëè÷åñòâî ïåðåñå÷åíèé äëÿ âåðõíåé èç èññëåäóåìûõ
òî÷åê áóäåò ðàâíî ÷åòûðåì (êàñàíèå çàñ÷èòàíî äâàæ-
äû), à äëÿ íèæíåé òî÷êè òðåì (êàñàíèå íå ó÷òåíî, à
ïåðåñå÷åíèå â âåðøèíå ëîìàíîé ó÷òåíî îäèí ðàç).
Ðèñ. 12
""" """!
l
Ïðîäîëæåíèå ñì. â ¹ 41
