Ammari H., Benkirane A., Touzani A. (editors) Recent Developments in Nonlinear Analysis
Подождите немного. Документ загружается.


December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
260
Let E be any measurable set in IR
N
, such that 0 < λ(E) < ∞. Then there
exists a positive constant C such that
Z
E
|u −u
E
| dλ ≤ C |||∇u|||
A,E
,
for all u ∈ W
1
A,loc
(IR
N
).
3) Let A be an N-function such that A and A
∗
satisfy the ∆
2
condition.
Suppose that IR
N
is A-hyperbolic. Let E be any non empty bounded domain
in IR
N
. Then there exists a positive constant C such that for all u ∈ E
0
A
(E)
Z
E
|u| dλ ≤ C |||∇u|||
A
.
Recall that for all f ∈ L
A
such that |||f|||
A
> 1, we have
R
A ◦ f dλ >
|||f|||
A
. We set s(A) = inf
n
log
R
A◦f dλ
log|||f|||
A
− 1, f ∈ L
A
, |||f|||
A
> 1
o
. Hence
s(A) ≥ 0. One can consult [37] for some examples of N-functions satisfying
s(A) > 0.
Now we are ready to solve the A-Laplace equation.
Theorem 9.3. Let L
A
be a reflexive Orlicz space such that s(A) > 0. Let
h ∈ L
∞
(IR
N
) have compact support. Then the equation ∆
A
u + h = 0 has a
weak solution u ∈ L
1
A
(IR
N
) if IR
N
is A-hyperbolic.
Remark 9.2. 1) We have in fact solved the equation in the space E
0
A
(D) ⊂
L
1
A
(IR
N
).
2) When A(t) = p
−1
t
p
, p > 1, L
A
= L
p
is the usual Lebesgue space,
we have s(A) = p − 1 > 0. Thus we recover the result in [94], when the
manifold M is IR
N
.
Corollary 9.2. Let L
A
(IR
N
) be a reflexive Orlicz space such that s(A) > 0
and α < N. Suppose that h ∈ L
∞
(IR
N
) has compact support. Then the
equation ∆
A
u + h = 0 has a weak solution u ∈ L
1
A
(IR
N
).
References
1. D. R. Adams, Traces of potentials arising from translation invariant opera-
tors, Ann. Scuola Norm. Sup. Pisa Cl. Sci. 25 (1971) 203-217.
2. D. R. Adams, Maximal operators and capacity, Proc. Amer. Math. Soc., 34
(1972) 152-156.
3. D. R. Adams, Traces of potentials. II, Indiana Univ. Math. J., 22 (1973)
907-918.
4. D. R. Adams, A note on Riesz potentials, Duke Math. J., 42 (1975) 765-778.
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
261
5. D. R. Adams, On the existence of strong type estimates in IR
N
, Ark. Mat.,
14 (1976) 125-140.
6. D. R. Adams, Sets and functions of finite L
p
-capacity, Indiana Univ. Math.
J., 27 (1978a) 611-627.
7. D. R. Adams, Quasi-additivity and sets of finite L
p
-capacity, Pacific Journal
Math., 79 (1978) 283-291.
8. D. R. Adams, Capacity and the obstacle problem, Appl. Math. Optim., 8
(1981) 39-57.
9. D. R. Adams, Lectures on L
p
-Potential Theory, Department of Mathematics,
University of Ume˚a, 1981.
10. D. R. Adams, The exceptional sets associated with the Besov spaces, in Linear
and Complex Analysis Problem Book. 199 Research Problems (V. P. Havin,
S. V. Hruˇsˇc¨ev, N. K. Nikol’skii, eds.), Lecture Notes in Math. 1043, 515-
518, Springer, Berlin Heidelberg, 1984. Also in Linear and Complex Analysis
Problem Book 3, Part II (V. P. Havin, N. K. Nikol’skii, eds.) Lecture Notes
in Math. 1574, 169-172, Springer, Berlin Heidelberg, 1994.
11. D. R. Adams, Weighted nonlinear potential theory, Trans. Amer. Math. Soc.
287 (1986) 73-94.
12. D. R. Adams, A note on the Choquet integrals with respect to Hausdorff
capacity, in Function Spaces and Applications, Proc. Lund 1986 (M. Cwikel,
J. Peetre, Y. Sagher, H. Wallin, eds.) Lecture Notes in Math. 1302, 115-124,
Springer, Berlin Heidelberg, 1988.
13. D. R. Adams, A sharp inequality of J. Moser for higher order derivatives,
Ann. of Math., 128 (1988) 385-398.
14. D. R. Adams and A. Heard, The necessity of Wiener test for some semi-linear
elliptic equations, Indiana Univ. Math. J., 41 (1992) 109-124.
15. D. R. Adams and L. I. Hedberg, Inclusion relation among fine topologies in
nonlinear potential theory, Indiana Univ. Math. J., 33 (1984) 117-126.
16. D. R. Adams, L. I. Hedberg, Function spaces and potential theory. Springer-
Verlag, Berlin, New York 1996.
17. D. R. Adams and J. L. Lewis, Fine and quasi connectedness in nonlinear
potential theory, Ann. Inst. Fourier (Grenoble) 35:1 (1985) 57-73.
18. D. R. Adams and N. G. Meyers, Thinness and Wiener criteria for nonlinear
potentials, Indiana Univ. Math. J., 22 (1972) 169-197.
19. D. R. Adams and N. G. Meyers, Bessel potentials. Inclusion relations among
classes of exceptional sets, Indiana Univ. Math. J., 22 (1973) 873-905.
20. D. R. Adams and M. Pierre, Capacitary strong type estimates in semi-linear
problems, Ann. Inst. Fourier (Grenoble) 41 (1991) 117-135.
21. D. R. Adams and J. C. Polking, The equivalence of two definitions of capacity,
Proc. Amer. Math. Soc., 37 (1973) 529-534.
22. R. Adams, Sobolev spaces, Acad. Press, New York, London, Torento, (1975).
23. R. Adams, On the Orlicz-Sobolev imbedding theorem, J. Func. Analysis, 24
(1977) 241-257.
24. H. Aikawa, Tangential boundary behavior of Green potentials and contractive
properties of L
p
-capacities, Tokyo Math. J. 9 (1986) 223-245.
25. H. Aikawa, Comparison of L
p
-capacity and Hausdorff measure, Complex
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
262
Variables, 15 (1990)223-232.
26. H. Aikawa, Quasiadditivity of Riesz capacity, Math. Scand., 69 (1991) 15-30.
27. H. Aikawa, Quasiadditivity of capacity and minimal thinness, Ann. Acad. Sci.
Fenn. Ser. A. I. Math. 18 (1993) 65-75.
28. N. A¨ıssaoui, Note sur la capacitabilit´e dans les espaces d’Orlicz, Ann. Sci.
Math. Qu´ebec. 19 (1995) 107-113.
29. N. A¨ıssaoui, On the continuity of Bessel potentials in Orlicz spaces, Collect.
Math. 47, 1 (1996) 77-89.
30. N. A¨ıssaoui, Instability of capacity in Orlicz spaces, Potential analysis, 6
(1997) 327-346.
31. N. A¨ıssaoui, Bessel potentials in Orlicz spaces, Revista Matem´atica de la
Universidad Complutense de Madrid, Vol. 10, N
o
.1 (1997) 55-79.
32. N. A¨ıssaoui, Some developments of strongly nonlinear potential theory, Lib-
ertas Mathematica, Vol.XIX (1999) 155-170.
33. N. A¨ıssaoui, On the continuity of strongly nonlinear potential, Math. Slovaca,
51 (2001), n
o
2, 215-228.
34. N. A¨ıssaoui, Capacitary type estimates in strongly nonlinear potential the-
ory and applications, Revista Matem´atica de la Universidad Complutense de
Madrid, Vol. XIV, num.2 (2001) 347-370.
35. N. A¨ıssaoui, Maximal operators, Lebesgue points and quasicontinuity in
strongly nonlinear potential theory, Acta Math. Univ. Comenianae, Vol
LXXI, 1 (2002) 35-50.
36. N. A¨ıssaoui, Strongly nonlinear potential theory on metric spaces, Abstr.
Appl. Anal., 7, no. 7, (2002) 357-374.
37. N. A¨ıssaoui, On the A-Laplacian, Abstr. Appl. Anal., 2003:13 (2003) 743-
755.
38. N. A¨ıssaoui, Weighted strongly nonlinear potential theory, Houston Journal
of Mathematics, 29, no. 1, (2003) 207-230.
39. N. A¨ıssaoui, Wolff inequality in strongly nonlinear potential theory and appli-
cations, African Diaspora Journal of Mathematics, Vol1, Number 1, (2004)
69-83.
40. N. A¨ıssaoui, Another extension of Orlicz-Sobolev spaces to metric spaces,
Abstr. Appl. Anal., 2004:1, (2004) 1-26.
41. N. A¨ıssaoui, Orlicz-Sobolev spaces with zero boundary values on metric spaces,
Southwest Journal of Pure and Applied Mathematics, 1, (2004) 10-32.
42. N. A¨ıssaoui, A. Benkirane, Capacit´es dans les espaces d’Orlicz, Ann. Sci.
Math. Qu´ebec. 18 (1994) n
o
1, 1-23.
43. N. A¨ıssaoui, A. Benkirane, Potentiel non lin´eaire dans les espaces d’Orlicz,
Ann. Sci. Math. Qu´ebec. 18 (1994) n
o
2, 105-118.
44. N. Aronszajn, F. Mulla, P. Szeptycki, On spaces of potentials connected with
L
p
classes, Ann. Inst. Fourier (Grenoble) 13 (1963) 211-306.
45. N. Aronszajn, K.T Smith, Theory of Bessel potentials, Ann. Inst. Fourier
(Grenoble) 11 (1961) 383-475.
46. A. Benkirane, Potentiel de Riesz et probl`emes elliptiques dans les espaces
d’Orlicz, Th`ese de Doctorat, U. L. B. (1988).
47. A. Benkirane and J. P. Gossez, An approximation theorem in higher order
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
263
Orlicz-Sobolev spaces and applications, Studia Math., 92 (1989) 231-255.
48. C. Fernstr¨om, On the instability of capacity, Ark. Mat., 15 (1977) 241-252.
49. B. Fugled, On the theory of potentials in locally compact spaces, Acta Math.,
103 (1960) 139-215.
50. B. Fugled, On generalized potentials of functions in the Lebesgue classes, Mat.
Scand., 8 (1960) 287-304.
51. B. Fugled, Le th´eor`eme du minimax et la th´eorie fine du potentiel, Ann. Inst.
Fourier (Grenoble) 15:1 (1965) 65-88.
52. B. Fugled, Quasi topology and fine topology, S´eminaire de Th´eorie du Poten-
tiel (Brelot-Choquet-Deny) 10 (1965-1966) no. 12.
53. B. Fugled, Applications du th´eor`eme minimax `a l’´etude de diverses capacit´es,
C. R. Acad. Sci. Paris S´er. A-B 266 (1968) 921-923.
54. B. Fugled, The quasi topology associated with a countably subadditive set
function, Ann. Inst. Fourier (Grenoble) 21:1 (1971) 123–169.
55. B. Fugled, Connexion en topologie fine et balayage des mesures, Ann. Inst.
Fourier (Grenoble) 21:3 (1971) 227–244.
56. B. Fugled, Finely harmonic functions, Lecture Notes in Math. 289, Springer,
Berlin Heidelberg, 1972.
57. B. Fugled, A simple proof that certain capacities decrease under contraction,
Hiroshima Math. J. 19 (1989) 567-573.
58. V. Gol’dshtein, M. Troyanov, Sur la non r´esolubilit´e du p-Laplacien sur IR
n
,
C. R. Acad. Sci. Paris 326 (1998), 1185-1187.
59. K. Hansson, Imbedding theorems of Sobolev type in potential theory, Math.
Scand., 45 (1979) 77-102.
60. V. P. Havin, Non-linear potential theory, Russian Math. Surveys 27:6 (1972)
71-148.
61. V. P. Havin, Use of (p,l)-capacity in problems of the theory of exceptional
sets, Math. USSR-Sb., 19 (1973) 547-580.
62. V. P. Havin and V. G. Maz’ya, Non-linear potential theory, Russian
Math.Surveys 27:6 (1972) 71-148.
63. L. I. Hedberg, Non-linear potentials and approximation in the mean by ana-
lytic functions, Math. Z. 129 (1972) 299-319.
64. L. I. Hedberg, On certain convolution inequalities, Proc. Amer. Math. Soc.,
36 (1972) 505-510.
65. L. I. Hedberg, Bounded point evaluation and capacity, J. Funct. Anal., 10
(1972) 269-280.
66. L. I. Hedberg, Approximation in the mean by solutions of elleptic equations,
Duke Math. J., 40 (1973) 9-16.
67. L. I. Hedberg, removable singularities and condenser capacities, Ark. Mat.,
12 (1974) 181-201.
68. L. I. Hedberg, Two approximation problems in function spaces, Ark. Mat.,
16 (1978) 51-81.
69. L. I. Hedberg, Nonlinear potential theory, in Potential Theory, Proc. Int.
Conf. Potential Theory, Nagoya 1990 (M. kishi, ed.) 43-54, de Gruyter, Berlin
New York, 1991.
70. L. I. Hedberg and Th. H. Wolff, Thin sets in nonlinear potential theory, Ann.
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
264
Inst. Fourier (Grenoble) 33:4 (1983) 161-187.
71. B. Jawerth, C. P´erez, G. Welland, The positive cone in Triebel-Lizorkin spaces
and the relations among potential and maximal operators. Contemporary
Mathematics, Proc. Conf. Boca Raton 1988 (M. Milman and T. Schonbek,
Eds.) 107, 71-971. Amer. Math. Soc., Providence, R. I, 1989.
72. M. A. Krasnosel’skii, Y. B. Rutickii, Convex functions and Orlicz spaces, P.
Noordhoff, Groningen (The Netherlands), 1961.
73. A. Kufner, O. Hohn, S. Fuˇc´ık, Function spaces. Academia, Prague, 1977.
74. W. A. J. Luxemburg, Banach function spaces. Thesis, Delft University, 1955.
75. V. G. Maz’ya, On the theory of n-dimensional Schrodinger operator, Izv.
Akad. Nauk SSSR. Ser.Mat. 28 (1964) 1142-1172.
76. V. G. Maz’ya, Polyharmonic capacity in the theory of the first boundary value
problem, Sibirsk. Mat. Zh. 6 (1965) 127-148.
77. V. G. Maz’ya, On (p,l)-capacity, imbedding theorems and the spectrum of a
self adjoint operators, Mat. USSR-Izv. 7 (1973) 375-387.
78. V. G. Maz’ya, Behaviour of solutions to the Dirichlet problem for the bihar-
monicoperator at a boundary point, Lecture Notes in Math. 703 , 250-262,
Springer, Berlin Heidelberg, 1979.
79. V. G. Maz’ya, Sobolev spaces, Springer-Verlag, Berlin-New York, 1985.
80. N. G. Meyers, A theory of capacities for potentials of functions in Lebesgue
classes, Math. Scand., 26 (1970) 255-292.
81. N. G. Meyers, Continuity of Bessel potentials, Isr. J. Math. 11 (1972) 271-
283.
82. N. G. Meyers, Taylor expansion of Bessel potentials, Indiana Univ. Math. J.,
23 (1974) 1041-1049.
83. N. G. Meyers, Continuity properties of potentials, Duke Math. J., 42 (1975)
157-166.
84. N. G. Meyers, Integral inequalities of Poincar´e and Wirtinger type, Arch.
Rat. Mech. Anal., 68 (1978) 113-120.
85. B. Muckenhoupt and R.L. Wheeden, Weighted norm inequalities for frac-
tional integrals, Trans. Amer. Math. Soc., 192 (1974) 261-274.
86. Yu. G. Reshetnyak, On the concept of capacity in the theory of functions with
generalized derivatives, Sibirsk Mat. Z., 10 (1969) 1109-1138.
87. Yu. G. Reshetnyak, On the boundary behavior of functions with generalized
derivatives, Sibirsk. Mat. Zh. 13 (1972), 411-419. English translation: Sibirian
Math. J. 13 (1972), 285-290.
88. M. M. Rao, Z. D. Ren, Theory of Orlicz spaces, Dekker Inc, New York, 1991.
89. J. Serrin, Local behavior of solutions of quasi-linear equations, Acta Math.,
111 (1964) 247-302.
90. J. Serrin, Removable singularities of solutions of elliptic equations, Arch.
Rational Mech. Anal., 17 (1964) 65-78.
91. T. Sj¨odin, Bessel potentials and extension of continuous functions on compact
sets, Ark. Mat., 13 (1975) 263-271.
92. E. M. Stein, Singular integrals and differentiability properties of functions,
Princeton Univ. Press, Princeton, New Jersey 1970.
93. A. Torchinsky, Interpolation of operators and Orlicz classes, Studia Math.,
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
265
59 (1976) 177-207.
94. M. Troyanov, Solving the p-Laplacian on manifolds, Proc. Amer. Math. Soc.
128 (2000) n
o
2, 541-545.
95. B. O. Turesson, Nonlinear Potential Theory and Weighted Sobolev Spaces.
Lecture Notes in Mathematics 1736, Springer-Verlag, Berlin, Heidelberg, New
York, 2000.
96. W. P. Ziemer, Weakly differentiable functions, Graduate Texts in Mathemat-
ics, Vol. 120, Springer-Verlag, New York, 1989.
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
266
Back on stochastic model for sandpile
Noureddine Igbida
LAMFA, UMR 6140, Universit´e de Picardie Jules Verne
33 rue Saint Leu, 80038 Amiens, France
E-mail: noureddine.igbida@u-picardie.fr
Our aim in this note is to give a simplified proof of the convergence of Evans-
Rezakhanlou Stochastic Model to the evolution surfaces model of sandpile.
Keywords: Evans-Rezakhanlou Stochastic Model; Convergence.
1. Introduction
The stochastic model for sandpile was introduced by Evans and Rezakhan-
lou in
6
as a variant of physical models for sandpile. It corresponds to a
Markov process
X(t)
t≥0
defined by an infinitesimal generator describ-
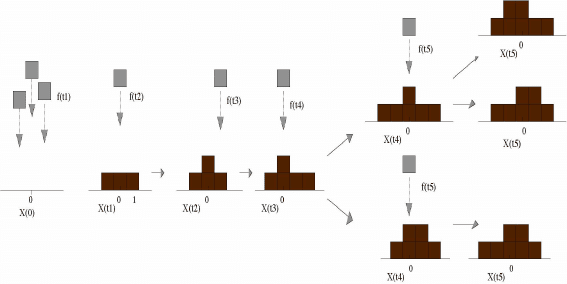
ing the evolution of stack of unit cubes resting on the plane when new
cubes are being added to the pile, by being placed either upon a heretofore
unoccupied square in the plane or else upon the top of a current column.
At each time t > 0, the configuration X(t) needs to be stable which means
that the heights of any two adjacent columns of cubes can differ by at most
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
267
one. So adding new cubes on existing pile, we ordain two possibilities to
each cube:
• if the configuration is stable, then the cube remains in place
• otherwise, the cube has several downhill ”staircases” along which it can
move, and the cube will randomly select among the allowable downhill
paths.
If we consider the case where the cubes can be also taken away, then a third
possibility may be ordain
• the cube has several ”upward staircases” along which it can move, and
the cube will randomly select among the allowable upward paths.
Assuming that we continuously add cubes at random locations on a starting
empty stack, Evans and Rezakhanlou studies the limit when one rascals
in both space and time, so as to consider growing piles of more and more
smaller and smaller cubes ? They prove that the macroscopic limit is rather
simple and very connected Prigozhin model for sandpile (cf.
8
and
2
).
Since the work of Prigohzin (cf.
8
see also
2
), this has been well known
(see also,
36
and the references therein) that the evolution of the surface of
the sandpile when the angle of stability is equal to π/4 can be described by
the following evolution problem
∂
t
u + ∂II
K
(u) 3 f
ˆu(0) = 0,
(1)
where K =
n
z ∈ W
1,∞
(IR
2
) ∩ L
2
(IR
2
) ; |∇z| ≤ 1
o
, ∂II
K
denotes the sub-
differential operator of the indicator function (cf.
4
) of K and f describes a
source term . Solution u is the height of the surface that grows up (resp.
grows down) under sand addition (resp. sand removal) by a source called f .
This is a critical slope model obtained by using the continuity equation and
the gradient constraint |∇u| ≤ 1 a.e. in IR
2
(see
8
and
2
for more details).
Existence, uniqueness and numerical approximation the solution are well
known by now for this model (cf.,
8
,
25
and
7
). More precisely, for any f ∈
BV
loc
(0, T ; L
2
(IR
2
)), we know that that (1) has a unique solution u in the
sense that u ∈ W
1,∞
loc
(0, ∞; L
2
(IR
2
)), u(0) = 0 and, for any t ≥ 0, u(., t) ∈ K
and
Z
IR
2
f(t, x) −∂
t
u(t, x)
u(t, x) − ξ(x)
≥ 0 for any ξ ∈ K. (2)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
268
To give the connection between the two models, let N be a large integer.
Assume the cubes are of side length O(N
−1
) and cubes newly and randomly
added at rate O(N
−1
) are continuously falling downhill. For the description
of the evolving of cubes, the authors of
6
introduce a probabilistic lattice
model. They thus consider a Markov process for the height X(t, i), defined
for times t ≥ 0 and sites i ∈ ZZ
2
. Resacaled source terms f
+
t
N
,
i
N
and
f
−
t
N
,
i
N
control the rate new cubes are added to the pile or removed
from it. Then, they proved that
IE
h
Z
IR
2
1
N
X
N t, [N x]
− u(t, x)
2
i
→ 0 as N → ∞, (3)
where u is the unique solution of (1). As shown in,
6
the key estimates for
the proof (3) are some kind of microscopic version of (2) (see (10)). To
prove these estimates the authors of
6
prove some elementary intermediate
estimates evolving various types of sets. Our aim in this note, is to improve
these key estimates directly by using some simple arguments.
In the next section, we recall the stochastic model of Evans and Reza-
khanlou. In Section 3, we prove the key estimates (10). Then, as in,
6
we
introduce the discrete evolution problem associated with (1). Then, we give
the proof of (3) by using some results of.
1
2. The stochastic model for sandpile problem (cf.
6
)
To describe the stochastic process for sandpile, we consider the lattice ZZ
n
.
We equipped ZZ
n
with an Euclidean norm and we say that i, j ∈ ZZ
n
are
adjacent, written i ∼ j, provided
|i −j| ≤ 1.
Without loose of generality, we restrict ourself to the cases n = 2, and we
write i = (i
1
, i
2
) to denote a typical site in ZZ
2
. Then, we introduce the
Hilbert space
H := l
2
(ZZ
2
) =
n
X : ZZ
2
→ IR ; kXk :=
X
i
X(i)
2
< ∞
o
.
A (stable) configuration is a mapping X : ZZ
2
→ ZZ such that
|X(i) −X(j)| ≤ 1 if i ∼ j
and X has bounded support.
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
269
The state space is
S :=
n
X : ZZ
2
→ ZZ ; X is a configuration
o
,
and the set of stable configuration is
ˆ
K :=
n
X ∈ H ; |X(i) −X(j)| ≤ 1 if i ∼ j
o
.
Let
ˆ
f : (0, ∞) × ZZ
2
→ ZZ be a function, such that f
+
(resp. f
−
) is
controlling the rate new cubes are added (resp. removed) to the pile. The
source of cubes
ˆ
f generates a stochastic process (X(t), t ≥ 0) in the state
space S. It is clear that the probability that X(t) be situated (at time t) in
a given set Γ of E, under the condition that the movement of the system
up to time s (s < t) is completely known, depends only on the state of
the system at time s. In other words (X(t), t ≥ 0) is a Markov process. To
study this process, we need to know its infinitesimal generator A, or more
precisely AF (X(t)) for any F ∈ B(S), the set of bounded functions. To
this aim, let us consider p
+
(i, j, ξ) the probability that a cube placed on
a given configuration ξ ∈ S at the position i will end up at j after it has
fallen downward over the stack with eight ξ. Likewise, let p
−
(i, j, ξ) be the
probability that the removal of a cube from the pile at i will result in a
removal at site j, after the cubes along a staircase each shifts downwards
to fill in the gap created at site i. So, for any i, j ∈ ZZ
2
we have
0 ≤ p
±
(i, j, ξ) ≤ 1 and
X
i∈ZZ
2
p
±
(i, j, ξ) = 1.
Thanks to,
6
we consider c
±
given by
c
±
(j, X, t) =
X
i∈ZZ
2
p
±
(i, j, X(t))
ˆ
f
±
(t, i), for any (t, j) ∈ ZZ
2
× [0, ∞).
(4)
The parameter c
+
(j, X, τ ) (resp. c
−
(j, X, τ )) is highly nonlocal factor and
records the rate, at time τ, new cubes come to rest at the site j after falling
downhill (resp. the rate at which cubes are removed from the site j, at time
τ). In particular, we have
X
j∈ZZ
2
c(j, X, t) =
X
i∈ZZ
2
f(t, i).
Thanks again to,
6
the infinitesimal generator A of the Markov process
