Aiserman M., Gusev L., Rozonoer L., Smirnova l., Tal A. Logic, Automata, and Algorithms
Подождите немного. Документ загружается.

370
ELEMENTS
OF
MATHEMATICAL LOGIC
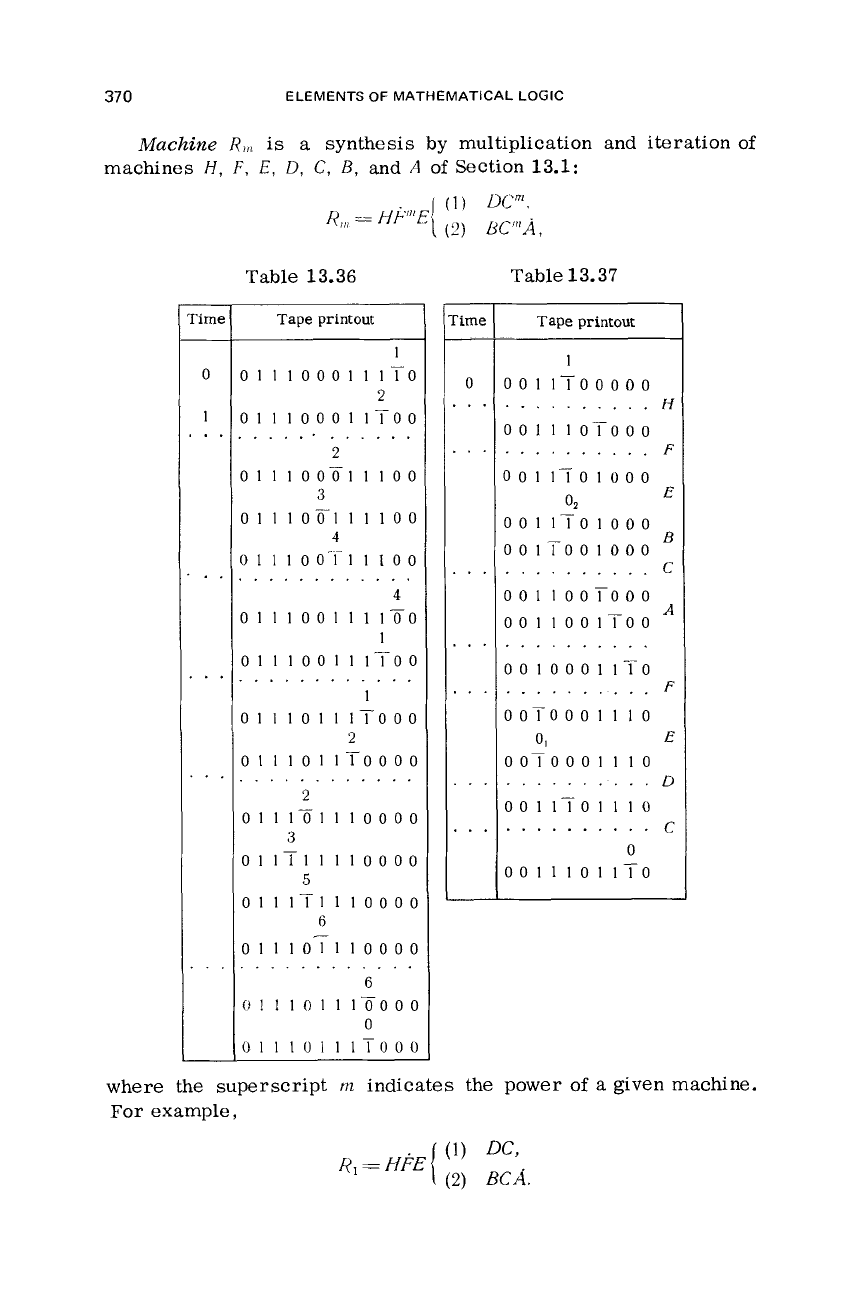
Machine
R,,,
is
a
synthesis by multiplication and iteration
of
machines
H,
F,
E,
D,
C,
5,
and
A
of
Section
13.1:
(
1
)
L)C"'.
i
(2)
BC"ZA,
K,,,
=
HPE
Table
13.36
Table
13.37
-
Time
0
1
...
...
...
...
Tape
printout
1
oi~iooo~i~io
0l1l00011T00
2
n
L
0ll1000lll00
01 11 001
11
100
0
11
1
Oo-lll
I00
3
4
4
011100111100
ollloolllToo
1
............
1
01110111T000
0l110llT0000
01
1101
110000
ollrlllloooo
olllrllloooo
2
............
2
3
5
6
olllorlloooo
............
6
0
0
1
11
0
11
loo00
ollIolllToo0
where the superscript
m
indicates the power
of
a
given machine.
For example,

COMPUTATION ON TURING MACHINES
37
1
Time
0
...
Machine
R,,
operates as follows:
if
the numbers
xl,
._.,
x,
are
represented on the tape in
the
standard position at
t
=
0,
then
R,,
prints the
first
of these numbers (thatis,x,) to the right of the rep-
resentation of
(XI,
. .
.,
x,)
and stops; after this, the tape contains a
system of
rn
+
1
numbers
(XI,
. .
.,
x,,
x,)
in standard position. How-
ever,
if
at
t
=
0
the tape contains, in standard position, the numbers
xI,
. .
.,
x,,
where
n
>
rn,
then R,, prints the number
xn
-,+
I
on the
right-hand side of
the
representation of this system of numbers and
stops;
after
this, the tape contains
the
number system
(xl,
x2.
.
.
,,
x,,,
x,-,+~).
An example of
the
operation of machine
R1
is
shown
in Table
13.37
(the
letters on the right indicate which of the com-
ponent machines of
RI
are responsible for a given step of
the
op-
eration;
the
symbols
O1
and
02
are the rest states of machine
E).
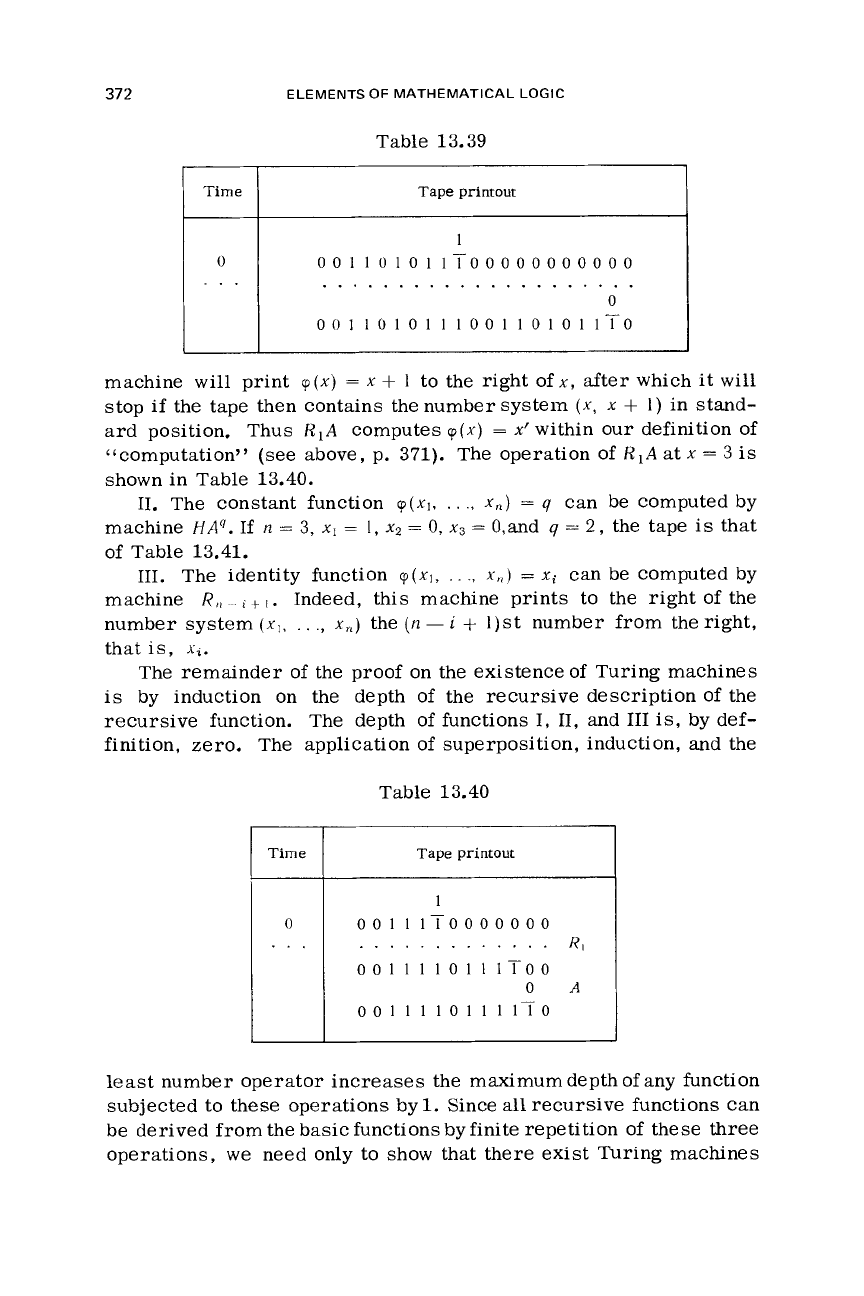
It can be shownthatthe mthpower
R,"
of
the
machine
R,
operat-
ing on numbers
(XI,
.
.
.,
x,)
in standard position, copies the entire
system next to and on the right-hand side of the original representa-
tion, the final result being a system
of
Zrnnumbers
(xI,
...,
x,,
xI,
. .
.,
x,)
in standard position. The starting and the final tapes
of
R$
at
rn
=
3,
x1
=
1,
x2
=
0,
and
x3
=
2
are shown in Table 13.38.
Tape
printout
1
oollololliooooooooooo
.....................
0
001101011101101011~00
372
ELEMENTS
OF
MATHEMATICAL LOGIC
Time
0
...
Tape printout
1
00llOl0lli00000000000
.....................
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
0
1
0
1
1
To
Table 13.40
Time
Tape printout
0
...
001111011li00
fl
001
11
101
11
170
1
001
1
li0000000
.............
Ri
least number operator increases the maximum depth of any function
subjected to
these
operations by
1.
Since
all
recursive functions can
be derived from
the
basic functions by finite repetition of these three
operations,
we
need only to show that
there
exist Turing machines

COMPUTATION ON TURING MACHINES
0
...
373
1
.............
H
A
'A
00ll010i00000
00ll010l0i000
0011010101100
0011010101110
Table
13.41
1
Time
1
Tape printout
I
capable of realizing the operations of superposition, induction and
the
least
number operator.
For simplicity,
we
shall avoid details of synthesis of Turing
machines realizing these operations and
shall
restrict ourselves to
the
simpler special
cases.
For example, instead
of
dealing with
superposition with respect to
n
variables,
we
shall
consider super-
position with respect to only one suchvariable.*
We
thus obtain the
following:
IV.
Superposition.
Let
M,
and
M,
be Turingmachines computing
the recursive functions
$(x)
and
x(x)
whose depths
are
CI
and
p,
re-
spectively.
We
desire
a
Turing machine
M,
computing the function
q(x)
=
x($(x))
with
a
depth
rnax(a,
0)
+
1.
This
will
be
accomplished
by the machine
MY
=
S,
M,
NM, NP.
V.
Induction.
Let
M,
be
a
machine computing arecursive func-
tion
x(x)
of depth
a.
We
shall devise
a
machine
M,
computing the
recursive function
q(x)
of depth
a
+
1
specified by the induction
scheme
'Q
(0)
=
qj
Y
(x')
=
x
('p
(4
)*
This machine
is
given by
(1)
BCP,
(2)
BCM,NP.
M,
=
S,Aq+'
FE
VI.
The smallest number operator.
Let
M,
be
a
machine com-
puting the function
~(x,
y)
of depth
a.
We
shall devise
a
machine
Mu
*For
a
precise description
of
generalized
Turing
machines
realizing
these operations,
see
1421.

374
ELEMENTS OF MATHEMATICAL LOGIC
computing the function
q(x)
=
pd/[x(x,
y)
=
01
of depthn
+
1.
Thisma-
chine
is
(1)
GFP,
(2)
GFA.
M,
=
S,GAM,E
Machine
M,
will
stop only
ifxsatisfies
the relation
(%~)[x(x,
y)
=
01.
We
shall now illustrate the computation by inductionand the use
of the smallest number operator
so
as
to elucidate
the
operation
of
machines
V
and
VI.
Table
13.42
Time
0
...
...
...
...
...
...
...
Tape
printout
1
001lT00000000000000000000
001
11001
l-~000000000,00000
0011100111011000000000000
........................
s,
........................
A‘’
........................
FE
0,
0011100111011000000000000~
OOlllOOlTOOllO0OOO0O00000
001110011001T000000000000
001110011001101111T000000
00ll100l100000ll11l000000
00l1100ll011llf0000000000
0011100110111110000000000~
001110010011l110000000000
0011100100111110000000000
001110010011111011111llT0
0011100100000000111111ll0
0011100101111 111i00000000
........................
c
........................
M
........................
N
........................
p
........................
FE
02
........................
c
........................
M
.......................
N
........................
P
........................
FE
0,
OolllOolollllllllOOoooOOoB
0011100001111111100000000
0011100001111111i-00000000
0011101111111~00000000000
........................
c
........................
F’
0

COMPUTATION ON TURING MACHINES
375
Time
0
...
...
...
...
...
...
...
...
...
...
Tape printout
1
00llT0000000000
001
1
l00l0000000
00111001011lliO
00111001~000000
001
1
l00T0000000
001
I
tooi~i-oooooo
A
o
o
I I I
o
o
1
I
0
1
1
I
To
001ll0oll000000
001
1
iooi~ioooooo
001110011-100000
A
...............
S,GA
...............
M,E
02
...............
G
...............
M,E
02
G
...............
...............
M,E
02
00
11
100
11
10
11-1-0
001 11001
1
l-d0000
oo111ooi11~ooooo
G
...............
0011100111T0000
A
...............
MXE
02
0011l0011110110
001110011110000
001110011170000
0011100111110io
00111001111103-0
0011100111110-00
O0lll00llllTO00
F
001
I101
1
Il'i-0000
...............
G
oo~i~ooiiiiiooo
A
...............
M,
01
E
P
0

376
ELEMENTS
OF
MATHEMATICAL
LOGIC
function
~(y)
while
keeping
a
check on how many times this compu-
tation
has
been repeated.
The result of the computation:
~(2)
=
7.
Selecting the operator of the smallest number.
Let
x(x,
y)
=
I
x2
-
y
I,
so
that
cp
(x)
=
PY[IX2-YI
=
01.
We
want to compute
~(2).
The machine operation
is
shown in Table
13.43:
here,
we
deter-
mine the consecutive values of
x(x,
0),
x(x,
I),
and
so
on, until
x(x,
y)
=
0.
The result of the computations
is
q(2)
=
4.
Let us also point out that
all
machines synthesized according to
schemes
I
-
VI
must be
so
designed that they
will
never go beyond
the left-hand
edge
of the tape.
We have thus shown that any recursive function can be
com-
puted on
a
Turing machine. It can alsobe shown that only recursive
functions
may be computed on Turing machines. This
is
proved by
means of g6delization
of
tape representations and verification of the
fact that any change in such representations can be expressed by
means of recursive functions
(see
the proof ofthis in
[42]).
By virtue
of
the equivalence of the concepts of “recursive func-
tion” and of “function computable on
a
Turing machine”,
as
well
as
by virtue
of
Church’s
thesis,
we
can now define an algorithm
as
follows:
An
algorithm is any procedure which reduces to the com-
putation of the values of aninteger-valued function
on
an appropriate
Turing machine

Conclusion
We
now return to the
two
fundamental problems posed in the
Introduction, namely:
(1)
Finding out what
a
finite automaton
or
a
sequential machine can and cannot rrdo,y3 and
(2)
the
development
of techniques for syntheses of devices which
are
dynamical sys-
tems of this
class
andperform specific
tasks.
The answers to these
problems have been gradually accumulating in the course of our
presentation of the theory.
We
shall
now endeavor to combine the
solutions scattered through previous chapters into one coherent
system.
1.
WHAT CAN A FINITE AUTOMATON
OR
A
SE
QU
EN
T
I
AL MACH
I
N
E
“DO“?
That depends whether the machine in question
is
autonomous
or
not.
If
the finite automaton
is
autonomous, then beginning with some
cycle
it
will
only generate
a
periodically recurring sequence of
states (the corresponding s-machine can only generate
a
fixed
se-
quence of outputs). If
this
is
a
one-symbol sequence, then
the
ma-
chine will achieve
a
state of equilibrium within
a
finite number of
cycles.
If this
is
a
multisymbol sequence, then the automaton
will
assume, one after another,
all
the states corresponding to
these
sequence, and
will
continue doing
so
ad
in,nitum.
That
is
all
an
autonomous machine can “do.”
However, regardless of what this finite periodic sequence of
states
is, one can always synthesize an autonomous finite automa-
ton which will start to generate
this
sequence
as
early as
its
second
cycle.
Because of that, and because
a
fixed cycle of successive
operations
is
characteristic
of
much
of
modern technology, dynami-
cal
systems which within allowable idealizations may be regarded
as
autonomous automata
are
widely used.
A
very old example of
such automata
are
the animated figurines which
go
through com-
plex sequences of motions, for instance, writing down
a
text on
a
piece of paper, playing predetermined music on an instrument, and
so
on. Modern examples range from washing machines to auto-
matic
lathes,
assembly lines and control systems for cyclic opera-
tions.
377

378
ELEMENTS OF MATHEMATICAL LOGIC
If
the automaton
is
nonautonomous, that
is,
its input state varies
from cycle to cycle, then the answer to the question of what it can
or
cannot ‘‘do” can be formulatedin avariety of terms, for example,
in the language of representation of events. Indeed,
a
nonautono-
mous finite automaton
(or
s-machine) merely transforms sequences
of input symbols into sequences of states
(or
outputs). Therefore,
if
we
ask
what suck a machine can
or
cannot do,
we
are
merely
specifying which sequences can be transformed in
a
given machine
and which cannot. But since the number of states
(or
of outputs, in
the case of
the
s-machine)
is
finite, our question
is
equivalent to the
following:
which
specific inputs produce
each
of the possible states
of the automaton
(or,
each
of the possible outputs of the s-machine)?
In the terminology of
the
theory of finite automata this question
is
formulated
as
follows: Which events can (andwhichcannot) be rep-
resented by each of the possible states of
the
automaton
(or
by each
of the outputs of the s-machine)? Theexactanswer, in terms of the
necessary and sufficient conditions for representability
of
events in
the
machine,
is
given by
the
theorems of Kleene. JSleene’s theorems
state that only regular events can be represented in
a
finite auto-
maton,
a
regular event being the input of sequence belonging to the
class of regular sets. Thus in the language of representation
of
events our question receives an unambiguous answer: Afinite auto-
maton can only represent regular events.
Many important input sets encountered in practice
are
known to
be regular.
For
instance, the following
are
regular:
(a)
the
set
consisting of any finite number of input sequences of finite length;
(b) the set of any periodically repeatinginput sequences;
(c)
the
set
of infinitely long sequences which always terminate in specified
finite sequences; and
so
on. However, in general,
if
we
are
faced
with an infinitelylong set of input sequences,
we
do not know
a
Pwri
whether this
set
is
regular
or
not. This
is
because
we
only have
techniques for
genevating
regular sets (by induction), but lack
ef-
fective solution for the inverse problem of finding out whether
a
given set
is
regular
or
not. Thus, even though the theorems of
Kleene do answer
the
question
as
to what
a
finite automaton can do,
the answer
is
not an effective one. Present research attempts to
construct other languages in which the answer could be given more
effectively. This language problem
is
also of cardinal importance
in the initial steps of the synthesis of automata, that is, it also fig-
ures in the second of the two problems formulated above.
Our
class
of dynamical systems consisting of “finite automaton”
and “sequential machine,’’ can be extended by providing the machines
with
an infinite memory (this can be done by letting the machine

THE
SYNTHESIS
OF
A
PRACTICAL
DEVlCE
379
have
an
infinite number of states, or providing it with an infinite
tape, and
so
on). This gives
a
broader
class
of abstract systems-
the Turing machines. The answer to the question, “what can they
do?”
is
much simpler: they can realize any
a
Pyiovi
specified
algorithm. Now in modern mathematics the algorithm itself
is
de-
fined
as
a
computation of values of some recursive function. And
since
we
know
so
precisely and unambiguously
what
a
Turing ma-
chine can do, we can use this machine to define the concept of the
algorithm.
We
thus close our chain of reasoning with the state-
ment:
an
algorithm
is
any process which can be realized in
a
finite
automaton supplemented by an infinite memory, that
is,
in
a
Turing
machine.
2.
THE SYNTHESIS
OF
A PRACTICAL
DEVICE
REALIZING A FINITE AUTOMATON OR
SEQU ENTl AL MACH
IN
E
If
we
wish to sample the input and the output of a system only
at
some specified discrete times (where these instants can either
be
specified
a
priOri,
or may be the resultof the very operation of the
system), then
we
have every reason to suspect that the device em-
bodying our requirements
will
be afinite automaton or an s-machine.
Since the object of the design
is
toensure the generation of desired
outputs in response to specified inputs,
we
could specify our device
by enumerating
all
the possible input-output relationships.
If this
enumeration results in
a
finite
list
of noncontradictory sequences
of
a
finite length,* then
we
can
be
sure that our specification can be
embodied by
a
finite automaton or an s-machine. Furthermore
given these input-output relationships,
we
can derive from them the
basic table of the
finite
automaton and the table of the output conver-
ter; together, these form one
of
the possible s-machines realizing
the specification (the algorithm for the synthesis of such tables
is
described in Section
8.2**).
It
is
much more difficult to ensure the generation of specific
outputs in response to infinitely long inputs. Such
cases
are
fre-
quently encountered in practice, when the duration of the operation
*We assume
a
peon‘
that either there canbe
no
other inputs,
or
that
if
there are such
inputs, then i.ie output may be arbitrary or, finally, that any other input
will
be signaled
by the appearance of some symbol indicating that input.
*This type
of
definitionis frequentlyencountered in the design of relay circuits, where
the required input-output relationships may be enumerated, for example, by means of the
so-called switching tables,
