Aiserman M., Gusev L., Rozonoer L., Smirnova l., Tal A. Logic, Automata, and Algorithms
Подождите немного. Документ загружается.


270
ELEMENTS
OF
MATHEMATICAL
LOGIC
Suppose
we
are given some slow s-machine
G
whose cycle (that
is,
clock rate)
is
governed by change of input. Let this
G
be given
as an interconnection matrix or
a
state diagram. The set
LG
of
G
contains
all
the possible sequences except those with
two
identical
symbols in a row.
We
need
a
fast s-machine
S
which reproduces
G
in terms of
Lc,
and whose clock rate
is
related to that of
G
in
the
following manner:
G
operates at instants
to,
t,,
t~,
.
.
.,
t,s
whichoccur
when
S
reaches equilibrium after any change ofinput. Assume that
the maximum number of fast cycles necessaryfor
S
to
go
from one
equilibrium state to another upon
a
change of input
is
in.
We
shall
then assume that, at reproduction, the
set
LG
of
S
contains
all
the
sequences such
as
P,"P,,
. .
.
P,, P,,P.,
-
.
P,,
.
.
r.
.
pmipoi
. . .
PCLi
(
PKi
+
PZi-+
,)
!
__y__
.-
(10.6)
40
times
4,
times
q1
times
where
qz
>,
m
for
all
i
=
I,
2
3,
.
. .
.
This means that an input
to
S
can-
not change until the machine
is
in equilibrium.
Assuming that
qz
>,
q",
the
set
of sequences such
as
(10.6),
will
be denoted by
TqT.
The sets
T,,*
satisfy the relationship
Tl~T22T22..
.
2T4*2..
.,
(10.7)
whereby
TI
=
E.
Thus, provided
q*
>,
rn,
any
set
T;
can serve
as
the set
L..
of
S.
If the condition of replacement of
G
by
S
specifies that the
two
machines must operate synchronously, then condition
q*
>,
m
means
that there
are
at
least
rn
cycles of
S
between two successive cycles
of
G.
We
shall
construct machine
S
by transforming the
state
diagram
of the given machine
G.
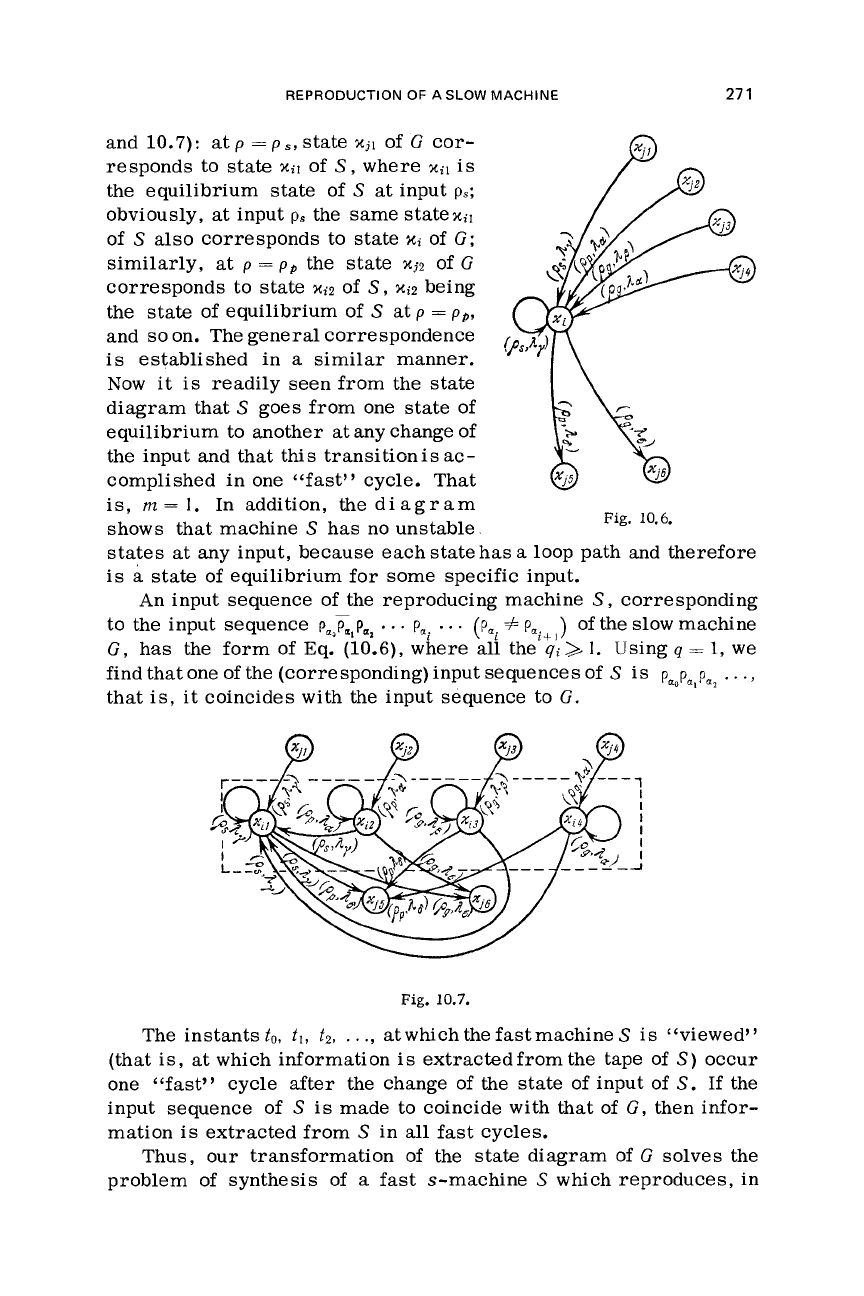
Assume that state
:ti
of
this diagram has the
form
of
Fig. 10.6.
We
shall replace
xi
with
as
many states
as
there
are different paths terminating in that state
(a
loop path
is
con-
sidered to be both terminating and originating in
state
Xi).
This
gives the four states
xL1,
xt2,
xLd,
xZ4
(surrounded by
a
dotted line) of
Fig.
10.7,
where each of these new states also carries
a
loop path
labeled in the same way as the path terminating in that state.
From
each of the new states
we
draw the same paths
as
those
which originated in state
xt
of Fig. 10.6; however,
we
need not draw
those paths carrying the same
p
symbol
as
the loop at the state from
which that path would originate
(see
Fig. 10.7).
We
do the same thing for all
states
of
G,
and obtain
the
state
diagram of
a
machine
S
which reproduces
G
in terms of
LG,
the
relationships between the states of
G
and Sbeing
as
follows (Figs. 10.6
REPRODUCTION
OF
A
SLOW
MACHINE
27
1
and
10.7):
at
p
=p.,state
xJ1
of
G
cor-
responds to state
xll
of
S,
where
xI1
is
the equilibrium state of
S
at
input
ps;
obviously, at input
ps
the
same statex,,
of
S
also corresponds to state
x1
of
G;
similarly, at
p
=
pp
the
state
xJ2
of
G
corresponds to state
31%2
of
S,
xt2
being
the state of equilibrium of
S
at
p
=
pp,
and
so
on. The general correspondence
is
established in
a
similar manner.
Now
it
is
readily seen from the state
diagram that
S
goes from one state of
equilibrium to another
at
any change of
the input and that this transitionis
ac-
complished in one “fast” cycle. That
is,
m=
1.
In addition, the diagram
shows that machine
S
has no unstable
states
at any input, because
each
state
has
a
loop path and therefore
is
a
state of equilibrium for some specific input.
An input sequence of the reproducing machine
S
,
corresponding
to the input sequence
P.&P,,
.
.
.
P,~
. . .
(pOL
+
pa,+,)
of the slow machine
G,
has
the
form of Eq.
(10.6),
where all the
q,>,
1.
Using
q
=
1,
we
find that one of the (corresponding) input sequences of
S
is
p,,p,,p,,
.
.
.
,
that is, it coincides with the input sequence to
G.
Fig.
10.6.
Fig.
10.7.
The instants
to,
tl,
tZ,
.
.
.,
atwhich the fast machine
S
is
“viewed”
(that is, at which information
is
extractedfrom the tape of
S)
occur
one
L‘fast9’ cycle after the change of the state of input of
S.
If
the
input sequence of
S
is
made to coincide with that of
G,
then infor-
mation
is
extracted from
S
in
all
fast
cycles.
Thus, our transformation of the
state
diagram of
G
solves the
problem of synthesis of
a
fast s-machine
S
which
reproduces, in

272
ELEMENTS
OF
MATHEMATICAL LOGIC
terms of
LG,
a given s-machine
G
responding to the change
of
the
input state.
Here
we
used the state diagram only for better visuali-
zation
of
the problem.
In
practice, it may be more convenient to
transform the interconnection matrix. This
is
done
as
follows:
Assume the interconnection matrix
CG
of
G
is
given, and let
it
conform to Fig.
10.6,
so
that its ith
row
and column
are
...
i
...
jS
...
j6
...
We
shall now replace this row and column with
as
many rows
and columns
as
there are different pairs in the ith column
of
CC.
Since there are
four
such pairs
[(ps,
A,),
(pp,
la),
(pg,Ap),
and(pg,
Xu)],
we
introduce the rows and columns
il,
i2,
i3
and
i4:
il
i2
i3
i4
...
j5
...
jG
J3
j4

REPRODUCTION
OF
A
SLOW
MACHINE
273
For diagonal elements of the submatrix comprising
these
four
rows and columns
we
take
(in any desired order) all the different
pairs of
the
ith column of
CG.
Furthermore, the intersection of row
jl
and column
i
of
CG
contains the pair
(pa,
A();
we
retain it in row
jl
of
the
new matrix
C,
but place
it
in the column where(p,,
AT)
is
already present, that is, column
il.
We
do the same with the pairs
of rows
j2,
j3
and
j4
of the ith column of
CG.
Now the columns
il44
are
complete, and
each
contain only identical pairs.
We
then
fill
in
rows
il-i4
of
C
as
follows: allthepairs of
the
ith row of
C"
[except
for pair
(ps,
h,)
whichis
present on the diagonal of
CG]
are
transposed
into
all
four rows
(ll-i4),
retaining these pairs in the same columns
as
in
Cc.
However,
if
the
p
symbol of the pair being transposed into
a
given row coincides with the
p
symbol of
a
pair already present in
that row, then there
is
no need for this transposition-the space
is
left blank. The pair
(ps,
A,)
is
transposedintoall rows
i144,
being
placed in that column in whichit already appears
as
a
result of
fill-
ing in the disposal elements. To be specific, the ith row of our ex-
ample of
CG
contains pairs
(ps,
AT),
(pp,
A,),
(pg,
AJ.
Row
il
of
C
already
contains pair
(ps,
A,)
;
we
transpose into itpair(p,,
h6)
and place it in
column
j5,
and the pair
(ps,
la)
incolumnj6.
We
add to
the
row
12
the
pair
(ps,
hr)
in column
il
and the pair
(&,A,)
in the columnj6 [pair
(pp,
La)
is
omitted from column
j5
since row
i2
already contains pair
(pp,
Am)].
Rows
13
and
i4
are
filled in the same manner.
The above procedure must be repeated for
all
the
ith rows and
columns of
CG.
As
a
result,
we
obtain
a
matrix
C
which actually
is
the
interconnection matrix
Cs
of the
fast
machine
S.
Note one prop-
erty of
Cs
:
all columns
of
this matrix contain (only) identical pairs.
It
is
obvious that
the
transformation of
the
interconnection ma-
trix
CG
into
CS
is
a
procedure identical to that employed in the pre-
viously described transformation of state diagrams.
Let
us
conclude
this
section with
two
notes.
Note
1.
In this section, just
as
in Section
10.2,
we
devised the
machine
S
so
Lcsuccessfully9' that
it
not only reproduces but also
represents machine
G.
In representation,
the
set
of allowed input
sequences may be any set, including
set
E,
since the inputs to
S
can
change
at
a
rate
coincidingwith the clock rate of the fast machine
S.
This
is
because
m
of
S
is
1.
In representation, the correspondences
between the states of
G
and
S
arethe same
as
in reproduction.
Note
2.
The above technique
is
only one of the available methods
for synthesizing
a
fast s-machine
S,
reproducing agiven s-machine
G
in terms of
LG.
Other techniques
are
also possible, since
S
is
not
the only machine reproducing
G
with respect
to
LG.
For
this
reason
there
arises
the problem of minimization of
S,
that is, the problem

274
ELEMENTS
OF
MATHEMATICAL
LOGLC
of synthesizing the machine
S
in such
a
way that it will contain
a
minimal number of states.
10.4.
MINIMIZATION
OF
THE S-MACHINE
OF
SECTION
10.3
We
shall
minimize the machine
of
Section10.3, that
is,
synthesize
a machine
SDli,
reproducing the given machine
G
in terms of
LG,
but
having the least possible number of internal states.
The required
machine
Smin
will
have to satisfy two conditions.
Condition
1.
Each state of
S,,,
must be an equilibrium state for
at least one input.
Condition
2.
Regardless of what changes
are
made
at
the input,
S,,in
must reach a new equilibrium in one fast cycle (that
is,
mSmin
=
1).
Fig. 10.8.
We
shall now prove that these conditions do not restrict the generality of
our
minimi-
zation. Assume that machine S,ni,,does not satisfy condition
1.
This would mean thatSmi,
has at least one statexh whichis not a state of equilibrium, and
is
represented in the state
diagram by a circle
h
not associated with a loop path (Fig. 10.8).
If
this
is
so,
we
can drop
this state
xh
from the diagram, replacing the path labeled
(pg,.
.
.
.)*
from
x,
to
xli
(and
passing through
xh)
by a direct path
(pg,.
.
.)
from
x,
to
%,I.
The path
(pS,.
.
.)
from
xh
to
xjP,
may be dropped because no path with the same label terminates in
7.h.
We
thus
obtain Fig. 10.9, from which all the nonequilibrium states have been removed.
This transformation modifies the operationSmI, only during the interval between two
equilibria of
Sm,,,
when we do not care what the machine does anyway. The order in which
the equilibrium states change remains unaltered and consequently the modified machine
will
reproduce the given machine
G
in the same way as before. However, the very fact
that
we
are able to reduce the number of states insrn,” by this transformation contradicts
our
statement that
Sluin
is
a minimal machine. Therefore a minimal machine Sminmust
satisfy condition
1.
Fig. 10.9.
*Dots in the label indicate that the output symbol can be arbitrary.

MINIMIZATION
OF
THE
s-MACHINE
OF
SECTION
10.3
275
In
general, for any givenmachine
G
there may exist several different minimal machines
Smin,each reproducing
G
in terms ofL,;. However, all these machines must have the same
number of states
kml,,,
Our
minization problem
will
be solved when
we
shall find at least
one of these machines.
Let
us
now turn to condition
2.
We
shall prove the following statement: if there exists
a machines,,,,", withk,,,,,internal states,reprcducingG in terms
LC
and not satisfying con-
dition
2,
then there must exist another machine
x,,,,,
with the same number of internal
states
kmi,,,
which also reproduces
G
in terms of
Lo
but which satisfies condition
2.
This
will show that condition
2
does not restrict the generality of the solution.
To
prove this
statement
we
shall show that the state diagram of
s",,,
can be obtained from that of
Smln
by
a
transformation which does not alter the number of states.
Let Sm,,go from state
xi,
which
is
an equilibrium forp
=
pp,
to state
xi
which
is
an
equilibrium for
p
=
pB.
Letthis beaccomplishedinm fast cycles. ThenSmln
will
go through
(m
-
1)
intermediate states
xii,
x,p,.
.
.,
xi(,,,
-
1)
(because none of these
is
an equilibrium
state, they cannot contain closed loops). For example, Fig. 10.10 illustrates what happens
in a section of some machine at
rn
=
3.
Fig. 10.10.
If
the
circles
i,
il,
i2,
.
.
.
,
l(m
-1)are directly connected to circle
j
by paths labeled
(ps,
A$),
then we obtain the state diagram
of
Fig. 10.11. Now
pp
shifts the machine from
state
xi
and from states
xil,
xi2,
.
.
.
,
,)to the state
xj
in one fast cycle.
If
we
transform
Fig. 10.11.
the entire-statediagramof Smlninthe same manner, then the state diagram of the resulting
machine_
Smln
will
have the same number of states. The operation of
Smln
will
differ from
that of
Smln
only during the intervals between equilibria, when
we
do not care what these
machines do anyway. However, an allowable input willchange the states of equilibrium in
Sml,input sequences in the same way as in
Smin.
This proves our statement.
Having proved that conditions
1
and
2
are
not restrictive,
let
us
look
for our minimal machine among the machines
S,,
SB,
S3,
.
.
.
,
which reproduce
the
given machine
G
in terms
of
LG
and
which
sat-
isfy these conditions.

276
ELEMENTS
OF
MATHEMATICAL
LOGIC
As
we
have already pointed out in the preceding section, repro-
duction requires that for any input sequence
(10.8)
of
machine
G
there be an input sequence
Pn0Pno
'
' '
Pa, P,,P,,
.
* *
Pa,
. .
Pa,Pas
.
*
.
Pas (Poi P,,+J
qdtimes-
4,
times
4$
times
of machine
S,
where
qi
>rn
(i
=
1,
2,
.
.
.).
Since
rn
=
1
for any
Si,
the set
L,?
of
input sequences allowedinSi can
be
any
set
T,*
(q*
=
1,
2,
3,
..
.)
of
sequences such
as
(10.6),
assuming
qi3,q*
(i
=
1,
2,
3,
. .
.);
in particular,
Ls
can be
the
set
E
=
TI.
Assume
we
want
Si
to reproduce
G,
andlet the
set
T?
be
used
as
the set
Ls
.
We
shall
then prove the following statement
(A):
if
state
xai
of machine
S,
and state
xp,
of machine
Sp
are
equivalent in terms
of set
T?,
then they
are
also equivalent with respect to
all
the
sets
T,,
T,
TB,
,
.
.
;
that
is,
they
are
simply
equivalent,
since
TI
=
E
(S,
and
S,
may also
refer
to the same machine).
If
q
>
p,
our state-
ment
is
obviously true, since in this
case
T4cT2
[see
Section
10.3,
Eq.
(10.7)].
If
q
<
;*,
the truth of our statement follows from the
fact that with any change of input,
all
machines
Si
will
go to
an
equi-
librium in one discrete instant, after which repetition of
an
input
symbol will not change the state
of
the machine, regardless
of
the
number of times this symbol
is
fed to the machine.
Every machine
Si
reproduces
G
in terms of set
LO,
that
is,
in
terms of
the
formula of
Eq.
(10.8).
This means that given any initial
state
x:
and
any allowedinput to
G
,
there
must exist an initial state
xi)
of
Si
at which that machine, accepting
a
corresponding input from
s,
set
Tq*
[in the form
of
Eq.
(lO.6)J
and observed only upon attainment
of equilibrium
after
a
change
of
input, generates
the
same output
as
G.
Without sacrificing generality, we may assume that
xo
will be
a
si
state of equilibrium for
Si
at
p
=
pmo;
were
this not
so,
then
Si
would
go in one "fast" cycle from
x!i
toxk which would have to be
a
state
of equilibrium at
p
=
p,,.
In that
case,
xiiwould be the
state
corre-
sponding to
x:
of
G.
Now consider any
two
machines
Si
and
Sj
from the
set
S,,
S1,
SB,
.
.
.
.
Suppose that at
p
=
p,",state
x:
of
G
corresponds to state
x$
of
Si
and to the state
x"
of
Sj.
Then, since states
x!.
and
xo
cor-
s/
respond to the same state of
G
for the same
pao,
th; outputs of
Si
and
Sj,
which start from
x"
and
x!j,
respectively,
will
coincide for
any input from
T?
which begins
witn
pa,,
this coincidence occurring
one "fast" cycle after
a
change of input. But
if
there
is
no change
of
input, then the machine
is
also in equilibrium at
all
other times,
and the outputs at
these
times
will
also coincide. Thus, the states
f
1
sI
.

MlNlMlZATlON
OF
THE s-MACHINE
OF
SECTION
10.3
277
x!t
and
x!,
are
equivalent at
all
those input sequences from
T,,
which
begin
with
pco.
But these states
will
also be equivalent in terms of
set
T,-,,
since they
are
equilibrium
states
at
p
=
p.,.
Indeed,
if
the
input sequence
were
to begin with some
pBo#
pa,,
then it would be
possible to write the sequence
I
(10.9)
which does begin with
p,,
and does belong toT4*.
With
respect to
this
sequence,
the
states
31"
and
x\
areequivalent.
At
the end of
q*
cycles,
the
machines star&g from these states,
are
again in these
states; thus the initial conditions
are
not changed, and
we
may take
the
(p
+
I)-th fast cycle
as
the reference time. If
we
do that, then
the sequence
(10.9),
taken
as
of the
(?
+
I)-th
fast
cycle, begins
with
pp.
Thus
we
have shown that
all
the states of
Si
(i
=
1,
2,
3,
. .
.)
cor-
responding to the same state
x:
of
G,
are
equivalent with respect
to the chosen set
T,-.
at
p
=
p,,.
It then follows from statement (A)
proved above that they
are
also equivalent with respect to
TI
=
E,
that
is,
they
are
simply equivalent.
Let us now assume that set
S,,
Sz,
S3,
.
.
.
yields
a
fast
machine
S
which not only reproduces
G
in terms of
LG,
but also represents
it
in terms of
E
*
This means that
for
each state of
s
and for any
p
=
p,,
we can find
a
state of
G,
such that there
is
representation.
Let
us
take any state
xs
ofS, and let
GS
be an equilibrium
state
for
p
pa,.
Then, under representation, the corresponding
state
of
G
is
xG.
Observing the operation of
s
and
G
of
various inputs
to
beginning with
pmo,
we
come to
the
conclusion that
if
Go
corresponds,
at
p
=
puo,
to
{$
under representation, then
x"_
corresponds, at the
same
p
,
to
xG
under reproduction (that is, machine represents
and reigoduces machine
G).
Since
g3
may be any
state
of
5,
it fol-
lows that for each state
ks
of
s
there
exist suitable
Go
and
pa,
of
G
such that
$
reproduces
xG
at
p
=
pa,.
But from
this
it follows di-
rectly that for any
state
Xs
of Sthere
exists
a
state
X.
equivalent to
it
in any machine
Si.
This means that
all
machines
Si
may be
mapped onto machine
3
(some of these
Si
may, of course,
also
be
equivalent to
3).
Therefore,
all
we
have to do
is
to minimize ma-
chine
s,
that
is
construct aminimal sequential machine
s,,,
equiva-
lent to
3.
And
this
can
be done by means
of
the Aufenkamp-Hohn
algorithm
(see
Section
9.6).*
The machine
S,,,
so
obtained
will
be
the minimal s-machine reproducing
G
in terms
of
LG.
I
-
S
'i
*For
machine
S,,
the decomposition
of
all
the states into groups equivalent in terms
of
set
T-,
coincides
with
groupings equivalent in terms
of
E.

278
ELEMENTS
OF
MATHEMATICAL
LOGIC
As
already pointed out in Section 10.2, the machine
S,
derived
by transforming the interconnection matrix of
G
,
both reproduces
G
in terms
of
LG
and representsitin terms of
E.
This machine also
satisfies
conditions
1
and
2
of
the present section. Consequently,
to obtain
S,,,,,
(to be precise, one
of
the possible minimal machines)
it
is suf8cient to minimize
S
by
symmetrical decomposition
of
its
intevconnectbn matvix.
The result
of
the minimizationdoes not de-
pend on
which
of the sets
T?
isused
as
the set
Ls
of input sequences
allowed in
S
under reproduction. In this
case,
restricting the num-
ber
of
sets
of
input sequences does not further reduce the number of
states of the reproducing machine.
We
shall
now construct
a
minimal s-machine
Smi,
reproducing
a
given machine
G
in terms
of
LG.
Example.
Let the interconnection matrix
CG
of
a
given “slow”
machine
G
operating in alphabets
(p)
=
11,
2,
3).
(x}=
(1,
2,
3)
and
{kj
=
{
1,
2)
be
1
23
(191)
(271)
(3,1)
I‘
cG=t
[
(2,2)“(1,2)
0
(3,l)
3
(2,2)V(1,1)
62)
0
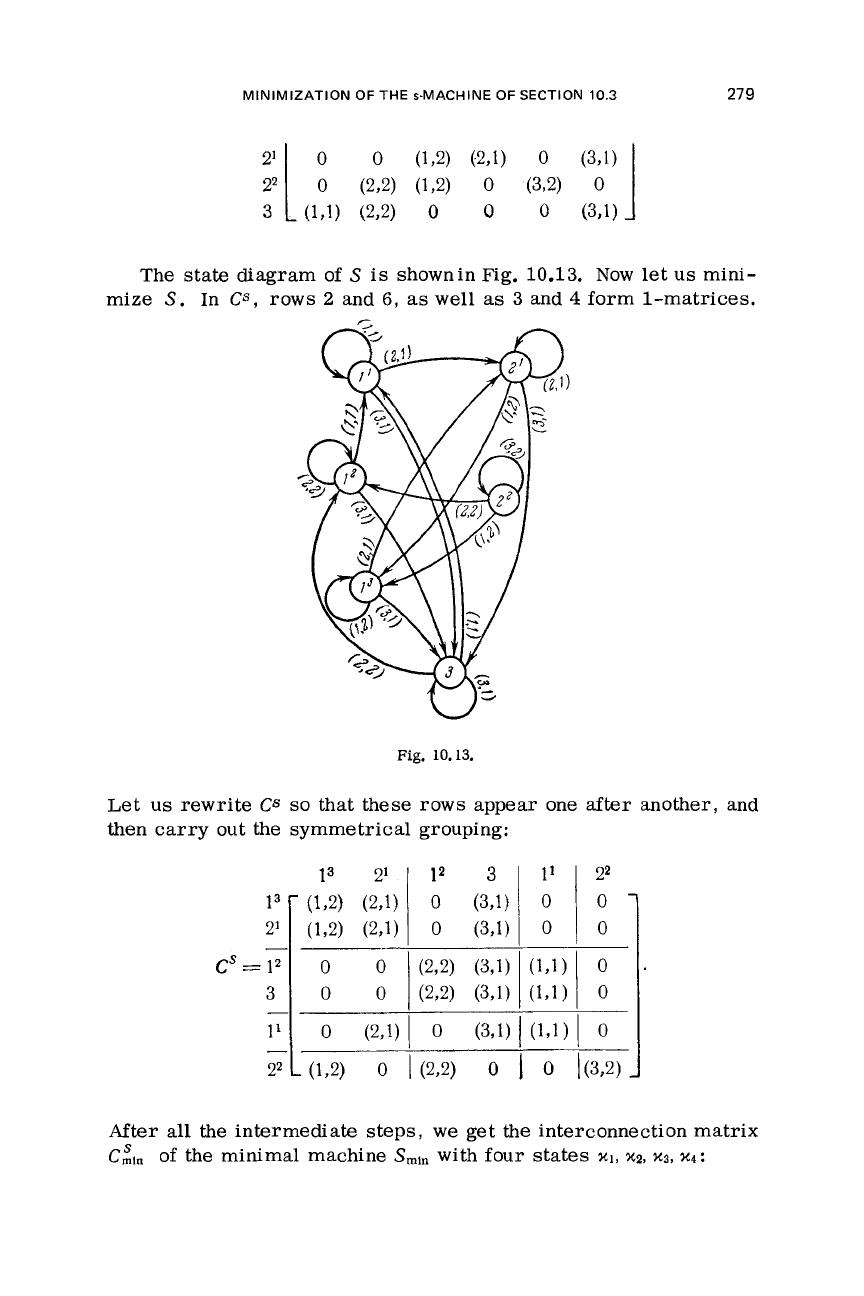
The state diagram of
G
is
shown in Fig. 10.12.
Fig.
10.12.
Tr*ansforming
CG
as
in Section 10.3,
we
obtain the matrix
Cs
of
the ‘‘fast’’ machine
S
reproducing
G
:
11
12
13
21
22
3
0
0
0
(3,1)
(1,l)
(2,2)
0
0
0
(3,l)
o
(1,2)
(2,i)
o
(3,i)
MINIMIZATION
OF
THE S-MACHINE
OF
SECTION
10.3
279
The
mize
S
Now
form
let
us
mini-
1
-matrices.
Fig.
10.13.
Let us rewrite
C*
so
that
these
rows appear one after another, and
then carry out the symmetrical grouping:
After
all
the intermediate steps,
we
get the interconnection matrix
C:,"
of the minimal machine
SmI,
with four states
XI,
XP,
x3, x4:
