Aiserman M., Gusev L., Rozonoer L., Smirnova l., Tal A. Logic, Automata, and Algorithms
Подождите немного. Документ загружается.


230
ELEMENTS
OF
MATHEMATICAL LOGIC
It
also
follows from the above thatifa
path labeled
(ps,
a,)
con-
then all the other similarly labeled paths from all the other states
nects a state
of
group
(XI,
XZ,
....
Xk}
withanotherstateofthatgroup,
{x,,
x2,
....
xk}
must also terminate in states belonging to thatgroup.
......
That is,
rw
path labeled
(ps,
L,)
leads to a state
%+I,
Xh+2,
Xn
outside the group.
will
be
If this
is
so,
then the interconnection matrix of
our
machine
7-1
...
..
..
"k+Z
c13
..
..
..
..
..
..
...
...
...
...
Here
all
the
submatrices
CI1,
Clz,
....
C1(,
-
k
+
,)
are 1-matrices
by virtue of the above italicized statements. The other submatrices
Cij
(where
i
=
2,
3,
....
n
-
k
+
1
and
j
=
1,
2,
....
n
-
k
+
1
)are
also
1-matrices since they
all
contain only one
row
(or
one member).
Our
arguments also hold in the general
case
where
there
are
sev-
eral
groups of pairwise equivalent
states.
However, some
of
the
individual states
Xk+1,
%+2,
....
3tn
must then be replaced by groups
of
states;
each of these groups behaves in
a
manner completely
analogous to the group{xl,
3t2,
....
x,)
of
our
particular
case.
This
concludes the proof of the theorem.
The Aufenkamp
and
Hohn theorem results in
a
simple and very
convenient algorithm for determining which groups of
states
of
a
given s-machine
are
equivalent.
This algorithm merely consists
of symmetrical decomposition of the interconnection matrix of the
given
s
-machine.
9.4
RECOGNITION
OF
EQUIVALENCE
OF
STATES
FOR
THE
CASE
OF
INPUT SEQUENCES
OF
LIMITED LENGTH
We
shall now consider
the
problem of equivalence of states when
the set
L
of allowable input sequences cannot contain sequences

CASE
OF
INPUTSEQUENCES
OF
LIMITED
LENGTH
23
1
comprising more than
q
symbols (that is, we analyze the operation
of the s-machine during the firstqdiscrete instants after
the
input).
It
is
required to find an algorithm recognizing those
states
which
are
equivalent in terms of
L
,
and to group these states together.
Since the total number of differing input symbols
pi
is
finite,
and since no sequence can contain more than
q
such symbols,
the
number of different sequences in set
L
must be finite. This being
the case, the required algorithm must exist.
To
ascertain that any
two
states
xi
and
xj
of
a
machine
are
equivalent in terms of
L,
it
is
sufficient to prove that given identical inputs from
L
,
the machine
starting from state
xz
will
generate the same output
as
the same
machine starting from
state
xj,
and that this
will
happen
at
all
pos-
sible inputs from
L
.
One can prove
this
by scanning either the state
diagram of
the
machine,
its
interconnection matrix,
or
any other of
its representations,
or
by an experiment on an existing machine.
The algorithm for recognizing equivalence thus entails scanning of
all
the input-output relationships which
are
possible for
a
given
set
of
two
states.
This obviously
is
a
huge task. One way of organizing
and, possibly, minimizing
this
unwieldy scanning procedure
is
to
raise
the interconnection matrix of the given s-machine to
a
power,
a
procedure described in Section
3.6.
Letus now recall the proper-
ties
of matrix
C4.
1.
The element
Cy,
of
C4
enumerates
all
those input sequences of
length
q
which shift the machine from
state
xt
to state
xj,
as
well
as
the corresponding output sequences.
2.
Since
the
state
of the machine at
t
=
p
+
1
is
uniquely defined by
its
state and input at
t
=
p
,
a
single row of
Cq
cannot contain
two
elements whose terms comprise identical input sequences.
3.
Each input sequence of length
q
must appear in each row of
Cq
.
Starting from these properties of
Cq,
one can derive the follow-
ing method for determining the
states
equivalentin terms of
L.
Let
us
arrange
set
L
in order of-increasing sequence length.
We
now
take
the shortest sequence of
L
(if
there
are
several such sequences,
all
of equal length,
we
can use any one of these), and
find
in matrix
Cq
(where
q
is
the maximum length of
a
sequence of
L
)
all
those in-
put sequences whose initial segments coincide with our shortest
sequence.
We
mark these coinciding segments in some way, for
instance, by placing dots over each of their constituent symbols.
We
repeat this procedure witheach successive sequence of
L
(sequences
of equal length can be taken in an arbitrary order). Each symbol of
Cq
is
marked
only
once; that is,
if
we
find
a
matching sequence in

232
ELEMENTS
OF
MATHEMATICAL LOGIC
Cq,
we place dots only over those symbols
which
are still unmarked.
This matching procedure finally gives a matrixwhich has sequences
carrying dots over all their symbols
as
well
as
sequences that have
only some initial segments marked, or no markingsat all.
For
example,
if
q
=
3;
the set
L
contains the four sequences
and the s-machine has the
state
diagram
of
Fig.
3.11
(for
its
matrix
C3
see Section
3.6),
then the matrix sequences are marked
as
follows:
After marking,
we
delete from
Cq
all
those input sequences
(to-
gether with the corresponding outputs)
which
do
not carry dots (in
our
example of
C3,
these
are
the sequences
0102p2
ana
02p2p1).
In in-
put sequences
where
dots appear only over the initial segments,
we
delete
the
unmarked symbols, that is, the tail ends.
We
also chop
off
the corresponding tail-end sections
of
the output sequences,
and
we obtain a
Cq
matrix
abm'dged
by
L.
For
example,
our
C3
matrix
is
abridged by
L
to give
Thus the abridged matrix contains only those input sequences
(and the corresponding outputs) which are present in
L.
Now
we
can

CASE
OF
INPUTSEQUENCES
OF
LIMITED LENGTH
233
define
a
simple scheme for recognition
of
equivalence of states:
Two
states
xi
and
xi
of
an smachine are equivalent in terms
of
L
if,
and only
if,
the pairs
of
input and outputsequences
ofrow
i
ofits
abridged (by
L)
Cq
matrix match exactly those
of
row
j
and there aye
no
unmatched pairs in either row.
Thus, in the abridged matrix of
our example there
are
no tworowswithexactly the same pairs, and
therefore this s-machine
has
no states equivalent to each other in
terms of
L.
However, even this algorithm, which
is
an improvement over the
disorganized scanning of all possible input-output relationships,
is
stillunwieldy, especially atlarge values
of
q.
For
this reason, one
tries to avoid the necessity of scanning allinput sequences from
L.
Instead, one tries to reduce each problem to those particular cases
where such scanning
is
not needed. Let us consider one such case.
Let set
L
contain
all
the sequences of length smaller
or
equal
to
q.
Set
L
is
a
subset of set
E
containing
all
input sequences.
For
that reason, any
two
states equivalent in terms of
E
(that
is,
simply
equivalent)
are
also equivalent in terms
of
L.
Now
we
have to
ask
ourselves when do groups of states of
a
given machine,
which
are
equivalent in terms
of
E,
coincide with
the
groups equivalent in
terms of
L;
that is, when
are
the states which
are
equivalent in
terms of
L
also equivalent in terms of
E?
If these two decomposi-
tions into groups coincide, then
we
can use the Aufenkamp
-
Hohn
algorithm:
however,
if
the groupings do not coincide,
we
may have
to resort to the scanning procedure described above,
or
to some
new method.
The answer to this question
is
associated with the relationship
between the number of states of the machine
k,
and the maximum
length of an allowable input sequence
q.
We
shall
show that
if
q
is
sufficiently large then it may be possible to recognize
all
the
non-
equivaEent
states. Then each pair of states nonequivalent in terms
of
E
will also be nonequivalent in terms of
L.
Assume that
we
are
given
a
sequential machine
S
with
k
states,
and that
we
symmetrically decompose
its
interconnection matrix
by means of
the
Aufenkamp
-
Hohn method. Now
we
have
k*
groups
of equivalent states (obviously,
k*
4
k).
We
shall try to prove that
if
q
>,
k*
-
1,
then the grouping of equiv-
alent states, obtained by the Aufenkamp
-
Hohn procedure, produces
groups which coincide
with
those equivalent in terms of
L
;
if
that
is
true, then at
q
>,
k*
-
1
we
can solve the equivalence problem by
means of the Aufenkamp
-
Hohn algorithm, and the number of result-
ing groups
will
indeed be equal to
k*.
Let us devise a machine
S*
having
k'
states and the following
characteristics:
(a)
for each state of machine
S
there
is
an equivalent

234
ELEMENTS
OF
MATHEMATICAL LOGIC
state of machine
S*
and, conversely, for
each
state
of machine
S*
there
is
an equivalent state of machine
S;
(b) no two states of
S*
are
equivalent. It will be shown in Section
9.7
that such
a
machine
can always be devised,
We
shall
now apply Moore’s theorem (Section 11.2)which states
that
if
a
machine
N
has
k
states
and
all
the states
are
nonequivalent
to each other, then for each pair of states
xi
and
xi
there always
exists an input sequence not longer than
k
-
1
that allows us to
dif-
ferentiate between these two states. Since
all
the states of
S*
are
painvise nonequivalent
[see
characteristic (b) above
1,
sequences not
longer than
k*
-
1
will
differentiate between
all
the nonequivalent
states of
this
machine. Therefore,
if
93,
k*
-
1,
all
these “differ-
entiating” sequences
are
contained in
L
,
all
states nonequivalent in
terms of
L
can be distinguished, and the Aufenkamp
-
Hohn algorithm
can be used.
However,
if
q
<
k*
-
1,
then the grouping in terms of
L
may not
coincide with the grouping with respect to
E.
In this
case
one may
be forced
to
resort to the scanning procedure in order to obtain
a
grouping in terms of
L
(one way of accomplishing such scanning
is
the
above method
of
raising matrix
C
to the power
of
9).
Sometimes one can avoid the scanning in such
cases
by estimat-
ing the lower bound of
the
number of states equivalent in terms of
L.
Thus
let
us partition matrix
C
into 1-matrices using only horizontal
lines. Then the
states
of the machine
are
divided into
rn
groups.
These
will
be groups of states equivalent with respect to
set
LI
of
all
the
input sequences of length
1
(set
Lf
coincides with the alpha-
bet
(PI,
p2, .
.
.
,
pr}).
Obviously, the number of groups of states equiv-
alent
with
respect to
L
cannot be
less
than
rn
,
since
9
1
and
Ll
E
L
and, consequently, any two states equivalent with respect
to
L
are
‘
also equivalent with respect to
L’.
Thus,
rn
is
the desired lower
bound.
For the same reason,
k*
is
the upper bound of
the
number
of
groups of states
which
are
equivalent in terms of
L
,
since
L
C
E
,
so
that any
two
simply equivalent
states
are
also equivalent in terms
of
L.
Thus,
if
rn
turns out to
be
equal to
k*
then, despite the fact that
(I
<
k“
-
1,
one can use
the
Aufenkamp
-
Hohn algorithm.
In the practical application of the Aufenkamp
-
Hohn algorithm,
m
and
k*
are
obtained
at
different stages of the computation. Thus
rn
is
obtained in the
first
stage, when horizontal lines
are
drawn to
partition matrix
C
into groups. If, however, the vertical lines drawn
subsequently to achieve symmetry “spoil”
this
grouping, then other
horizontal lines must be drawn, and
so
on,
so
that ultimately one

EQUIVALENCE, MAPPING AND MINIMIZATION
2
35
one obtains
k*>
m.
Thus one knows immediately whether the
Aufenkamp
-
Hohn algorithm
is
applicable.
Restricting our discussion of
the
equivalence problem to the
cases described in this and the previous sections,
we
shall make
two
brief observations regarding other definitions of the allowable input
sequences
L.
1.
One important
case
(particularly in the theory of relay-con-
tact
circuits)
is
that where
L
contains all sequences in which no
two
identical symbols are repeated consecutively. It can
be
shown that
for this case there
exists
an algorithm for recognizing equivalent
states. However, the present authors know of no algorithm which
would be suitable for practical use.
2.
If Aufenkamp constraints are operative, then the very
state-
ment
of
the problem must be changed: in this
case
it
makes no sense
to talk of
two
equivalent states
x1
and
xj
since
states
x,
and
xI
may
allow different
sets
of input sequences.
Here
L,,
may be forbidden
in
xJ,
and vice versa. However, in
this
case
one may sometimes use
a
concept which
is
akin to that of equivalence. This
is
the concept
of compatibility of states, which
is
defined as follows:
Two
states-state
x,
of machine Sand state
c,
of machine G-are
said to be compatible
if,
and
only
if
both machines-machine
S
in
initial state
x,
and machine
G
in initial state
CJ
-having acquired any
input
sequence from the intersection*
of
set
LK,
with set
Lr,,
will
generate identical output sequences(in particular,
S
and
G
may be
the same machine).
In accordance with
this
definition, states
x,
and
&
must be compatible
if
that intersection
is
an empty set, that
is,
if
states
xl
and
5,
have no allowable input sequences in common, If
LK,
and
Lc
coincide then,
of
course, compatibilityreduces
to
equiva-
lence in drms
of
the common
set.
Now, the group of states
{XI,
XZ,
. .
.
,
3tk)
is
said to be
agroup
of
pseudoequivalent states
if, and only if, any
two
states
x,
and
x,
of
that group are compatible. This concept
is
frequently very useful;
in particular,
it
can be applied for minimization of an s-machine
which
is
subject to Aufenkamp constraints
(see
Section
9.8).
9.5.
EQUIVALENCE, MAPPING AND MINIMIZATION
OF
SEQUENTIAL MACHINES
So
far,
we
discussed the equivalence of individual states; now
we
shall turn to the equivalence of entire s-machines.
*An
intersection
of
two
sets
contains
all
points belonging to both
sets.

236
ELEMENTS
OF
MATHEMATICAL LOGIC
Two
s-machines,S and G,are said to be equivalent in terms
of
L
if,
and only
if
for each state
x,
of
S
there exists atleast one state
5,
of
G
equivalent to it in terms
of
L
and, conversely, ifforeach state
G
of
(;
there exists
at
least one state
HI
of
S
equivalent
to
it
with re-
spect to
L.
This definition
says
any input sequence from
L
must be allowed
both in
S
and
in
G.
If
the set of
all
scquences allowed in
S
is
Ls
,
and
the analogous set for
G
is
LG,
then
L
must satisfy the condition
where
L,nL,
denotes the intersection of sets
Ls
and
LG.
When
I,
=
E
(that
is,
I,
contains
all
the possible sequences),
we
shall
say
that the machines
S
and
G
are
simply equivalent.
In this
case
Ls
=
Machine
S
maps onto machine
G
in terms of set
L
(or
G
maps
S
in terms of
/.)
if,
and onlyif, for each state
xi
of
S
there
exists
at
least one state
;,
of
G
equivalent to it in terms of
L.
If
L
=
E,
then
S
simply
maps
onto
G.
From our definitions of mapping and equivalence
we
can deduce
the following:
if
machine
S
maps onto machine
G
in terms of
L,
and
G
maps onto
S
in terms of the same
L,
then
S
and
G
are
machines
which are equivalent in terms of
L.
The equivalence relationship between
S
and
G
is
denoted by
S
-
G,
while
the mapping of
S
onto
G
is
written
as
S
c
G.
Equivalent machines
are
identical
as
far
as
processing of input
sequences into output sequences
is
concerned.
If machine
S
maps
(or
maps in
terms
of
L)
ontomachine
G,
then this means that
G
sub-
stitutes for
S
(however, the converse
is
not true).
Consider two equivalent s-machines
S,
and
Sz,
and let their
states be partitioned into groups of equivalent states.
Now
we
take
some such group
s;
of
S,
and select any state
x,
from this group.
Then
S2
will
have
a
state
x1
equivalent to
xz.
Let
x,
belong to the
group (of equivalent states)
sj
of
S,.
If
that
is
so,
then any
state
belonging to
s;
of
S,
is
equivalent to any state belonging to
sj
of
S,.
However, none of the states of
sy
of
S,
is
equivalent to any of
the states of
s:
of
S,
,
if
7
+
8.
Therefore, each group of equivalent
states of
SI
corresponds to one and only one group of equivalent
states of
Sz.
The symmetry of the equivalence relationship (it fol-
lows from
S,
-
Sz
that
Sz
-
Sl),
implies that the converse statement
is
also true, that
is,
each group of equivalent states of
S2
corre-
sponds to one, and only one group of equivalent states of
S,.
Accord-
ingly, the
two
equivalent machines
Sl
and
S1
contain the same number
Lc
=
L
=
E.

UNRESTRICTED SET
OF
ALLOWABLE INPUT SEQUENCES
237
of groups of equivalent states, andmachines
S,
and
S2
differ
only in
the number of states in each of
the
corresponding equivalent groups.
If, however, we
are
giventwomachinesS and
G
such that
G
maps
S
(S
c
G),
there
is
no one-to-one correspondence between their groups
of equivalent states:
all
we
cansayis that to each group of equiva-
lent
states
of
S
there corresponds one and only one group of equiva-
lent states of
G.
However, the converse
is
not true. Accordingly,
G
may have more groups of equivalent states than
S;
thus, machines
S
and
G
may differ not only in the number of states in each (equiv-
alent) group, but also in the number of (equivalent) groups.
All
of the above also holds
if
we consider equivalence and
mapping in relation to
a
set
L
restricted
per se.
Now let us discuss the minimizationof ans-machine
S.
Minimi-
zation of an s-machine
S
with respect to
a
set
L
(of allowable
se-
quences) shall mean finding another s-machine
G
satisfying these
two
conditions:
1)
G
maps
S
(GIS)
with respect to
L.
2)
There
is
noothers-machine mappingsin terms of
L
and con-
taining
fewer
states than
G.
An
s-machine
G
satisfying these conditions
is
said to be
minimal
for
S
in
terms
of
L.
Let us point out that
if
there exists an algorithm for recognizing
states
equivalent in terms of
L
then, in principle, there also exists
a
trivial minimization algorithm in terms of
L.
Indeed,
if
machine
S
has
k
states, then the number of internal states in
G
(which
is
minimal for
S)
cannot exceed
k.
In principle, therefore,
we
could
scan
all
the machines whose number of states does not exceed
k
(there
is
a
finite
number of such machines). And since there must
exist an algorithm for recognizing
states
equivalent with respect
to
L,
we
can check whether each of
these
machines maps
S.
Ob-
viously, such
a
trivial algorithm has no practical value, and
we
would
like
to find practical algorithms.
So
far, such an algorithm exists
only for the
case
where
all
input sequences are allowed.
We
shall
describe it in the next section.
9.6.
MINIMIZATION
OF
A SEQUENTIAL MACHINE WITH AN
UNRESTRICTED SET
OF
ALLOWABLE INPUT SEQUENCES
Let
S
be
a
sequential machine with
k
internal states decomposed
into groups of equivalent states
as
in Section
9.3.
(Figure
9.5
shows
a
section
of
the state diagram of this machine.) Consider the first
of these groups. Its states
are
the
termini of paths from other states.
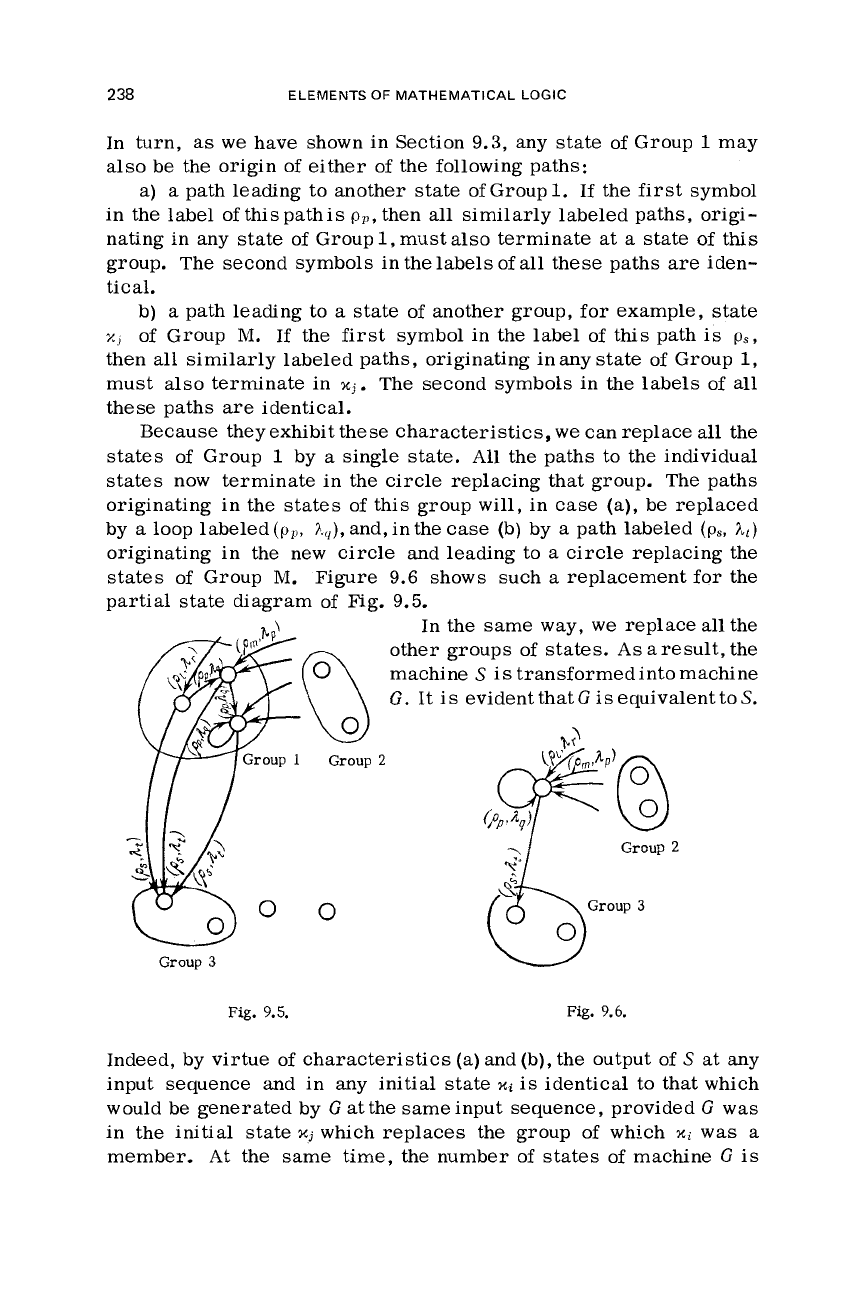
238
ELEMENTS
OF
MATHEMATICAL LOGIC
In turn,
as
we
have shown in Section
9.3,
any state of Group
1
may
also
be
the origin
of
either of the following paths:
a)
a
path leading to another state of Group
1.
If the first symbol
in the label
of
this pathis
pPr
then
all
similarly labeled paths, origi-
nating in any state of Group
1,
must also terminate at
a
state
of
this
group. The second symbols in the labels of
all
these paths
are
iden-
tical.
b) a path leading to
a
state of another group, for example, state
X,
of Group
M.
If the
first
symbol in
the
label of this path
is
ps,
then
all
similarly labeled paths, originating in any state of Group
1,
must also terminate in
x~.
The second symbols in
the
labels of
all
these paths
are
identical.
Because they exhibit these characteristics,
we
can replace
all
the
states
of
Group
1
by a single state.
All
the paths to the individual
states now terminate in the
circle
replacing that group. The paths
originating in the states of this group will, in
case
(a),
be
replaced
by a loop labeled
(pP,
?.,[),
and, in the case
(b)
by
a
path labeled
(ps,
hl)
originating in
the
new
circle
and
leading to
a
circle
replacing the
states
of
Group
M.
Figure
9.6
shows such
a
replacement for the
partial state diagram of
Fig.
9.5.
In the same way,
we
replace
all
the
other groups of
states.
As
a
result, the
machine
S
is
transformed into machine
G.
It
is
evident that
G
is
equivalent to
S.
roup
1
Group
2
Group
2
Group
3
Group
3
Fig.
9.5.
Fig.
9.6.
Indeed, by virtue of characteristics
(a)
and (b), the output of
S
at any
input sequence
and in any initial state
is
identical to that which
would be generated by
G
atthe same input sequence, provided
G
was
in the initial state
1cj
which replaces the group of which
xi
was
a
member. At the same time, the number
of
states
of machine
G
is

UNRESTRICTED SET
OF
ALLOWABLE
INPUT
SEQUENCES
239
equal to the number of groups
of
equivalent states
of
S,
and one can-
not further reduce this number by combining these
states
into
groups.
It has been shown in Section 9.5 that
all
equivalent machines have
the same number of equivalent groups, and that
the
number
of
such
groups in machines mapping such equivalent machines cannot be
lower. Thus
a
minimal machine cannothave
fewer
states
than
there
are
groups
of
equivalent
states
in the machine being minimized.
For
this reason, machine
G
is, indeed, minimalfor
S.
It follows from
this
that,
in the absence of bounds on the set of inpidt sequences
,
(a)
the minimal
machine belongs to the class of equivalent machines
,
and
(b)
the minimization problem is merely one offindinggroups of
equivalent states, that
is,
it can be solved
by
means of the Aufen-
kamp
-
Hohn algorithm
(see
Section 9.3).
Since this algorithm
is
used,
it
is
convenient to work with ma-
trix
C
rather than the
state
diagram, and replace groups of states
by
a
single one directly in the matrix. For example, consider
the
matrix
C
of Section 9.3
XI
7-2
7.3
7-4
7-5
C=
y.6
By
symmetrical decomposition into 1-matrices
we
obtain
Thus
we
have three groups of equivalent states,
(XI,
xd),
{~s},and
The replacement
of
groups
of
states
of
a
state diagram by
a
single state
is
equivalent to the replacement
of
each 1-matrix
of
the symmetrical decomposition by
a
single element, whichis
a
dis-
junction (union)
of
all
the elements of the 1-matrix being replaced.
bz,
x5,
X6).
