Aiserman M., Gusev L., Rozonoer L., Smirnova l., Tal A. Logic, Automata, and Algorithms
Подождите немного. Документ загружается.


170
ELEMENTS
OF
MATHEMATICAL LOGIC
this reason depth relates to
a
specific regular expression
rather
than to
a
regular
set.
Let
us
also point out that
a
subset of
a
regular set of input
se-
quences may not necessarily be regular. This follows from the
simple fact that a universal set
is
regular by definition,
whereas
irregular sets do exist (for an example of
an
irregular set,
see
Section
7.6).
The reader
will
recall that the sequences treated
so
far
in
this
section did not carry anumber identifying the discrete time at which
they appeared at the input.
Let
us
now consider a set
S
of such sequences and identify each
element
of
this set
with
a
number describingt.
We
start with
t
=
0.
Then
we
obtain
a
set
of
input tapes from
a
set of input sequences.
Thus,
for
example, a set consisting of the three input sequences
becomes
a
set consisting
of
the three input tapes
rnent
A
set of input tapes formed by such
a
method from
a
regular set
of input sequences will be called
a
regular set
of
input tapes.
We
shall
associate with each regular set of input tapes the same regular

REPRESENTABILITY
OF
REGULAR
EVENTS
171
expression that describes the corresponding regular set of input
sequences.
We
can now proceed to the classification of events at the input
of the automaton.
An input event
of
the automaton is said to be vegulav
if
the set
of
input tapes (each examined completely
fvorn
t
=
0
to
t
=
p)
defining
the occuvence
of
the event is
a
vegulav set.
Among regular events
we
may distinguish
a
subclass of events
that
are
described by
a
regular expression
where
A
is
any
set
of finite input sequences containing not more
than
q
symbols. Such
a
regular event
is
known
as
a
specific event
of
length
q
or
simply
a
specijZc event.
With
a
specific event, one
need not examine
the
entire input tape from
t
=
0
to
t
=
p
in order
to specify it: one merely looks over
a
length
q
of
the
“tail end”
of
the tape, corresponding to
t
=
p,
p
-
1,
p
-
2,
. .
.,
p-
q.
One can
visualize this process
as
one in
which
the input tape
lies
under
a
transparent runner (similar to hairline-carrying runner of
a
slide
rule) through
which
one can observe only some number
q
of tape
positions.
With
each discrete instant the runner
is
displaced one
position to
the
right,
so
that the extreme right position seen through
the runner always corresponds to
t
=
p
.
Specific events
are
distinguished by
the
fact that
we
can
so
select
the runner
(a
specific one for each specific event) that at any time
p
the occurrence or nonoccurrence
of
an event
is
indicated simply by
those positions on the input tape that can be seen through that runner.
7.4.
REPRESENTABILITY
OF
REGULAR EVENTS
We
can now formulate and prove the following fundamental theor-
ems.
Kleene’s first theovem. Assuming a suitable initial state
of
the
automaton, any vegulay event can be repvesented in
a
finite auto-
maton equipped with an output convevtev
by
genevation
of
1
at
the
output
of
the convevtev.
We
shall prove this theorem by showing one of the possible
methods for synthesizing
an
automaton representing
a
regular event
defined by an arbitrarily chosen regular expression.
*
*Another
proof
of
this theorem
is
given in Chapter
8
in connection with the descrip-
tion
of
Glushkov’s method.

172
ELEMENTS
OF
MATHEMATICAL LOGIC
We
shall now introduce
auxiliary
automata
with output convert-
ers
(the converter output may only be
0
or
1)
having, in addition to
input
p,
auxiliary inputs for symbols
a
from the alphabet
(0,
I}.*
Assume that
a
regular set of input sequences
R
is
given.
We
shall
say that an
event
R,
occurs at the input of the auxiliary automaton
at time
p
if
there
exists
a
time
t
(0
4
t
<
p)
such that:
1)
the symbol
a
=
1
appears
at
the auxiliary input
at
t;
and
2)
the
sequence of symbols
p
that appear between times
t
and
p
belongs to
R.
For
example, let the given set
R
include the three sequences
Then, given the input tape of our auxiliary automaton (Table 7.4),
the event
R,
will
only occur at times
3,
5,
7,
14, and
18.
We
shall say that the generation of symbol
1
at the output of the
converter for
the
auxiliary automaton represents the event
R,
if, and
only
if,
the event
R,
occurs at the input of this automaton.
Table 7.4
mi
PI
P2
?3
P5
?3
P2
PI
1110101
Now let us imagine that there
is
an autonomous automaton with
an output alphabet
{O,
I}
and that the output of this automaton coin-
cides with the
wire
a
of the auxiliary automaton (Fig.
7.1).
The
whole network
so
obtained constitutes an automaton with
a
single
input
p.
Further, let the autonomous automaton generate an output
of
a
=
1
at time zero, and
a
=
0
at
all
subsequent times. Then our
network will represent the event
R
by
generating an output of
1.
Such an autonomous automaton can, indeed, be synthesized: this
may be, for example,
a
binary delay element whose input
is
always
zero,
while
its
initial state
is
1.
Therefore,
if
we
can show that an
auxiliary automaton representing the event
R,
can be synthesized
*in
other
words,
the
input
symbols
of
such
an automaton are
symbol
pairs
(p,
1)
or
(P3
0)
*

REPRESENTABILITY
OF
REGULAR EVENTS
173
regardless
of the type of regular
- -
-
-
- -
-
-
-
-
-
-
-
-
event
R,
then we shall have proven
the senting existence any regular of an automaton event
R.
repre- Our
g!Z'IG
Auxiliary
proof
will
be inductive and be based
on the depth of the regular expression
defining the regular event
R,
being
automaton
represented.
We
shall
show
first
a
way of representing
all
regular events
Ra
with
a
zero depth of the defining
regular expression
R.
Then
we
shall prove that
if
a
regular event
R,
defined by
a
regular expression
R
of arbitrary depth
v
can be
represented, then any regular event
R,
defined by
a
regular expres-
sion
R
of depth
v
-k
1
can also be represented.
Recall that regular expressions of depth
zero
are
simply symbols corresponding to the given input sequences
a,
b,
c,
.
.
.,
as
well
as
the symbol
E,
corresponding to the universal
set
of input sequences.
Representation of the event
R,
de-
noted by symbol
E
means devising an
automaton with
an
output of lmaintained
from the first instance whena
=
1
regard-
less
of what the input sequence may be.
Such an automaton may be synthesized
from, among others,
a
binary delay unit
that
is
in
its
zero state
at
1
=O.
The input to this unit, via
a
dis-
junction element,
is
a
symbol
a
and anoutput symbol* (Fig.
7.2.).
Let us now construct an automaton representing the event
R,
when the set
R
contains only one input sequence of finite length
q.
This machine consists of
two
delay lines (each with
q
delay units)
and
a
symbol converter
(Fig.
7.3).
The
first
(main) delay line oper-
ates
in alphabet
{p},
and the second (auxiliary) in binary alphabet
{a}.
The converter output
is
1
if, and only if, the symbols
p
at the outputs
of
all
the delay units of the main line form one given sequence of
length
q,
counting from the end of
the
delay line toward its beginning.
The
initial
state
of the delay units in
the
main line
is
immaterial,
but
all
such units in the auxiliary line must be in
state
zero. The
output of the automaton
is
a
conjunction of the outputs of the con-
verter and the auxiliary delay line.
The output
will
be
1
if, and onlyif:
1)
at
q
discrete instants prior
to the sampling instant
p
there
is
an input of
1
at
a
(and therefore
automaton
Autonomous
Fig.
7.1.
First inductive step,
Fig.
7.2.
To
make this automaton conform to
our
other automata, we can assume that it
also
has an input
p,
but that
its
output does
not
depend
on
p.

174
-
:
Q,-
q
delay
units
-
----
a
~
t
ELEMENTS
OF
MATHEMATICAL LOGIC
-
output
&--t
L
Fig.
7.3.
the auxiliary line has an output of
1
at
t
=
p)
and
2)
there
is
an in-
put of the given sequence of symbols during the
q
discrete
instants
preceding
p
(and therefore there
is
aconverter output of
1
at
t
=
p
).
It
is
seen from
Fig. 7.3 that there cannot be an output of
1
until
q
discrete instants after
t
=
0
(since at
t
=
0
all
delay
units in the aux-
iliary line
are
in state zero). It follows from this that the states of
the delay units in the mainline donot affect the output
of
the system
at
t
=
p
;
that
is,
q
instants after
t
=
0,
the
states of these delay units
are determined only by the inputs.
This completes the first part of our proof. That
is,
we
showed
that the system of Fig. 7.3 represents an event
R,
where
R
is
any
regular expression of depth zero.
We
now proceed to the second
part
of
the proof.
Induction,
We
shall now prove that
if
thereexist auxiliary auto-
mata that represent events
R,
specified by any desired regular ex-
pressions
of
depth
v
(v>
0).
thenwe can synthesize an automaton that
Will
represent the event
R
specified by any desired regular expres-
sion of depth
v
+
1.
From the definition of the concept “depth of
a
regular expres-
sion” it follows that any regular expression of depth
v
+
I
is
obtained
from one
or
two
regular expressions of depth
v
via
a
single multi-
plication, iteration,
or
union of
sets.
In this connection, and in order to complete the induction, it
must be proved that
if
events
R,,
specified by regular expressions
R,
and
R2,
are
representable, then events
R,,
specified by expres-
sions
are also representable.
Let
us
consider these three operations separately.
For
the
sake
of brevity and wherever there
is
no
risk
of ambiguity,
we
shall
de-
note the regular expression, the event corresponding to it, and the
automaton representing the event
R,
by the same letter
R.

REPRESENTABILITY
OF
REGULAR EVENTS
175
Union
of
sets
An automaton representing
a
union
is
obtained from
two
automata, respectively representing
R,
and
Rz.
This
is
done by connecting their inputs and feeding their outputs
to
a
common disjunction element (Fig.
7.4).
Multiplication.
An automaton representing
a
product
is
obtained from
two
automata, representing
RI
and
Rz,
respectively,
by feeding the output of automaton
RI
into the auxiliary input of
Rz
via
a
delay unit (Fig.
7.5).
Then the auxiliary input line of
RI
be-
comes the auxiliary input to
the
system,
while
the
output of
Rz
is
the
output of
the
system. Indeed, the output of
RZ
will be
1
if
R2
repre-
sents an event that
has
begun during the instant following
an
output
of
1
in
R,.
But
an
output of
1
in
R1
means
that
the event
R1
had
al-
ready been represented prior to that instant, and that
this
event had
begun at the instant of occurrence of
1
at the auxiliary input of
Ri
(and therefore at the input of our entire automaton system). Conse-
quently the automaton system
as
a
whole represents the event
R,
which
is
described by: “the event
Rz
occurred directly
after
the
event
&,7i
that is,
the
product
R,
.
Rz.
ll
I-
Fig.
7.4.
Fig.
7.5.
Iteration.
If the automaton
R1
representing the event
R1
is
given,
then the automaton representing an
RE
event:
R
=
(Ri)
may be ob-
tained by coupling
RI
toone disjunctionelement
(Fig.
7.6).
The dis-
junction element output
is
made to coincide with the auxiliary input
to
R,
,
while the input of disjunctionelement consists of the auxiliary
input
a
to
Rl
as
well
as
the
RI
output, which
is
made to pass through
a
delay unit. Indeed, the output of
this
system
is
1
whenever the
event
Ri
is
represented, starting with the appearance of
1
at the
auxiliary input
a,
or
from the instant directly following the repre-
sentation of the event
R,.
Therefore, there
is
a
system output of
1

176
ELEMENTS
OF
MATHEMATICAL
LOGIC
whenever
the
event
R1
occurs (this can
happen any number of times in succes-
sion),
which
is
what indeed constitutes
the representation of event
R
=
(R*).
This concludes the induction process
based on
the
depth
of
the
regular
ex-
pression, and therefore completes the
proof of the entire theorem.
First note.
Our
formulation of
Kleene’s first theorem included the statement about
the
choice of
a
suitable initial state. It
can
be seen from
the
proof that
a
suitable
choice of the initial state reduces to:
a)
ensuring
a
state
of
0
in
all
units of the auxiliary delay line during representation of the given
set consisting of one input sequence (Fig.
7.3);
b) ensuring
a
state
of
1
in the delay unit of the automaton representing
a
universal
event (Fig.
7.2);
and c) ensuring
a
stateof
1
in the delay unit of the
autonomous automaton representing
the
event
t
=
0
(see
above).
Second note.
The representation of the event
ER
differs from
that of
the
event
R
only in the method of utilizing the auxiliary input
of the automaton which represents the event
R,.
To be precise, in
order to represent the event
R
,
this input
is
connected to the autono-
mous automaton
which
produces
1
only
at
t
=
0;
however, in order to
represent the event
ER
,
this input consists of the output of the auto-
maton representing the event
E
(Fig.
7.2);
that is, this input
is
always
1.
This applies, inparticular, to the representation of
a
spe-
cific
event
E.
a.
Fig.
7.6.
7.5.
REGULARITY
OF
REPRESENTABLE EVENTS
In this section
we
shall prove
a
theorem that
is
the converse of
the one proved above.
Kleene’s second theorem. Only regular events are representa-
ble in a jinite automaton.
To prove this theorem we shall
first
introduce the concept of
regular sets of triad chains, then
we
shall prove an auxiliary lemma,
and finally with the help
of
this
lemma,
we
shall prove
the
theorem.
The infinite set of
tapes which may be generated in
a
finite automaton contains only
a
finite numberlzrof different triads. Letus denote these by
PI,
PZ,
.
.
.,
phrand match
each
triad
pi
to
a
point in
a
plane.
The
tviad
labyrinth and labyrinthine paths.
REGULARITY
OF
REPRESENTABLE
EVENTS
177
bl
r"t;/
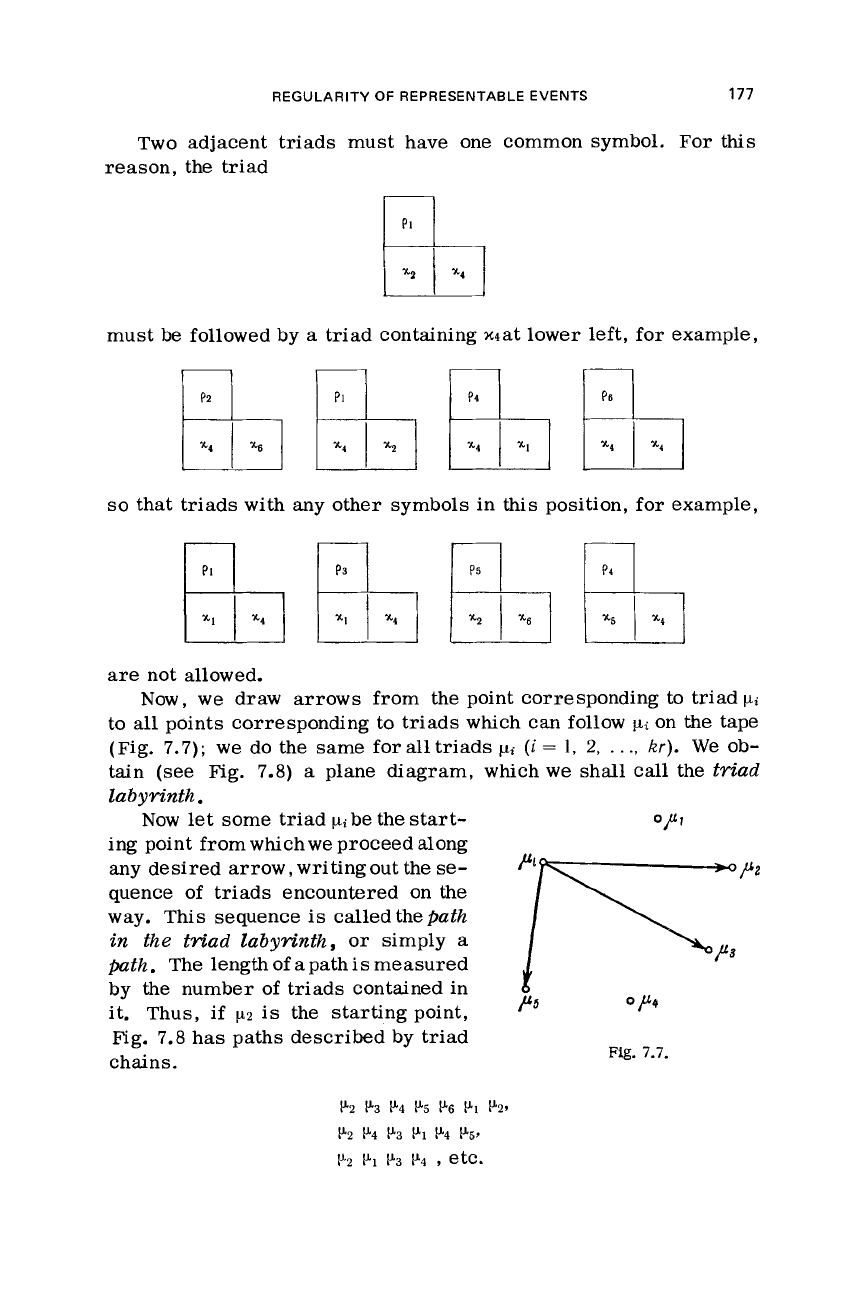
Two adjacent triads must have one common symbol.
For
this
reason, the triad
,::
1
%
must be followed by a triad containing x4at lower left, for example,
so
that triads
with
any other symbols in this position, for example,
Fig.
7.8
has paths described by triad
chains.
Fig.
7.7.
178 ELEMENTS
OF
MATHEMATICAL
LOGIC
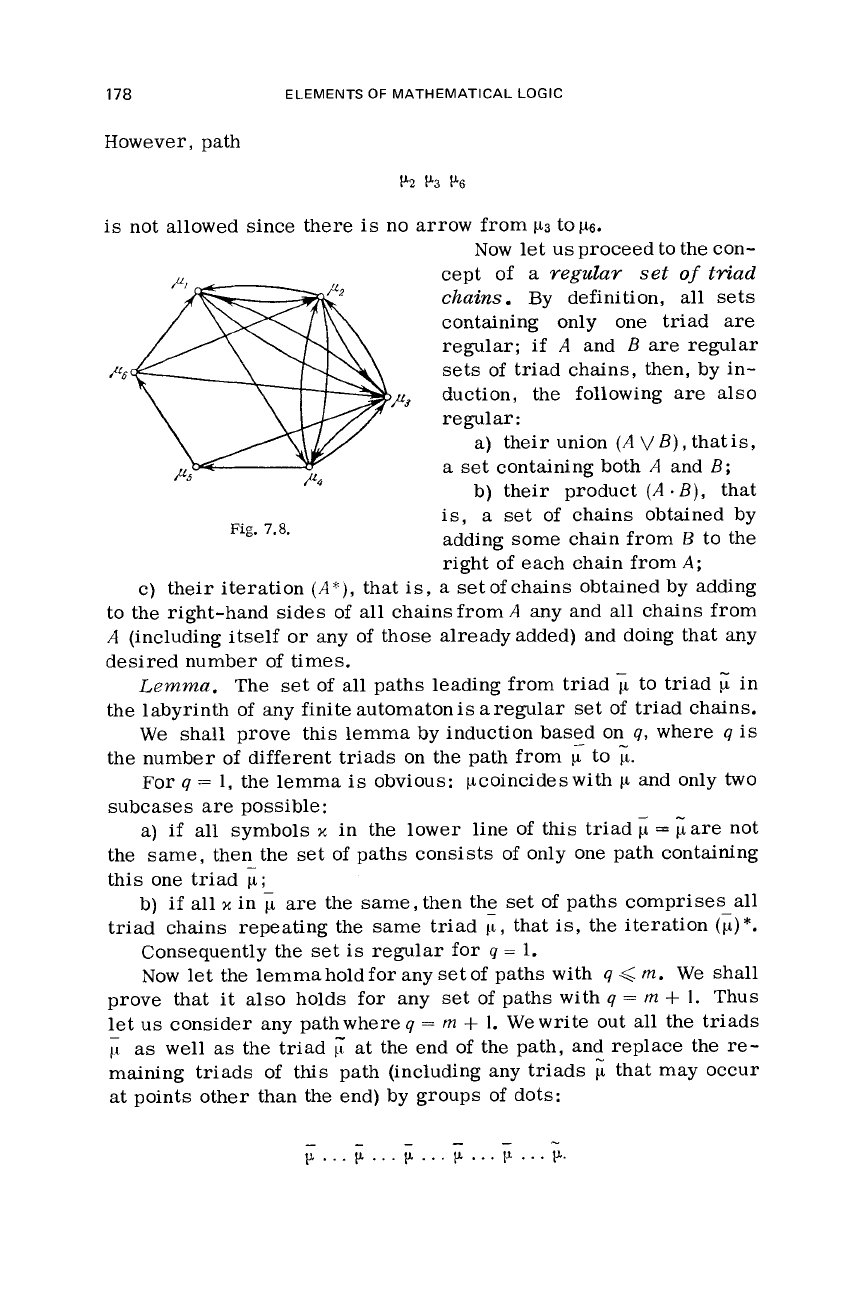
However, path
is
not allowed since there
is
no arrow from
p3
top6.
Now
let
us proceed to the con-
cept of
a
regular set
of
triad
chains.
By definition,
all
sets
containing only one triad
are
regular;
if
A
and
B
are
regular
sets of triad chains, then, by in-
duction, the following
are
also
regular:
a)
their union
(A
V
B),
thatis,
a
set
containing both
A
and
B;
b)
their product
(A.
B),
that
is,
a
set of chains obtained by
adding some chain from
B
to the
right of each chain from
A;
c)
their iteration
(A*),
that is,
a
setofchains obtained by adding
to the right-hand sides of
all
chainsfrom
A
any and
all
chains from
A
(including itself or any of those alreadyadded) and doing that any
desired number of times.
Lemma.
The set of all paths leading from triad to triad in
the labyrinth of any finite automatonis aregular
set
of triad chains.
We
shall
prove this lemma by induction based on
q,
where
9
is
the number of different triads on
the
path from
p
to
p.
For
q
=
1,
the lemma
is
obvious: pcoincideswith
p
and only
two
subcases
are
possible:
a)
if
all
symbols
3t
in the lower line of
this
triad
p
=
pare
not
the same, then the set of paths consists
of
only one path containing
this one triad
i;
b)
if
all
x
in
are
the same, then the
set
of paths comprises
all
triad chains repeating the same triad
L,
that is, the iteration
(;)*.
Consequently the set
is
regular for
q
=
1.
Now let the lemma hold for any set of paths with
q
<
m.
We
shall
prove that it also holds for any set of paths with
q
=
m
+
1.
Thus
let
us
consider any pathwhere
q
=
m
+
1.
Wewrite out
all
the triads
11
as
well
as
the triad at the end of the path, and replace the
re-
maining triads of this path (including any
triads
;
that may occur
at
points other than the end) by groups of dots:
Fig.
7.8.
--
--
-
-
-
--
-
-
p...p...p...p...p...p.

REGULARITY
OF
REPRESENTABLE EVENTS
179
Each group of dots stands for
a
path that
does
not contain the
triad
1..
For
this
reason,
the
number of different
triads
contained
in each path replaced by
a
group of dots
is
smaller than
m
+
1
by
at
least
1,
that is,
q
<
m.
By induction, each path replaced by dots
is
a
regular
set
of triad chains.
We
shall denote
these
replaced paths
by
Ti,
rj,
rg,
and
SO
on.
To start with,
let
p
=
p.
Then one can imagine the entire path
from to
p
=
p
as
consisting of triads
F,
with
the
regular sets
r
interspersed among them.
We
write this
as
follows:
---
--
--
-
-
-
-
-
-
-
-
-
__
-
vi
rri
rr,
r
rr,
. . .
t"rq
r.
In this notation, the entire path consists
of
pairs
of
consecutive
paths. Each such pair
is
the product
of two
regular
sets:
a
set con-
sisting of
a
single element
i,
and the corresponding set
;.
Conse-
quently, such
a
pair must itself belong to
a
regular
set
-
p.
There-
fore,
all
paths leading from
p
to
p
=
p
are
elements
of
the iteration
---
of
p'R
6.Ry.F;
that is, they constitute
a
regular set
of
triad chains.
from
,i
to
;L"
is
If
i#
then by the same reasoning the set
of
all
paths leading
G.
R)*.
t.;
that
is,
it
is
also regular. The lemma
is
thus proved.
This lemma can be readily ex-
plained on
a
triad labyrinth.
Consider the triadlabyrinth of Fig.
7.9
(where some arrows have been
omitted for clarity), and run through
the possible paths from
p
to
p.
First, there
is
a
choice of thetwo
paths
9
F
--
r.12
3i
and
6
u
8
9
10
F.
Fig.
7.9.
Second, the first path may be lengthenedbyincluding
a
loop, for ex-
ample,
p1235764123;.
