Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

and

The vector F

¥F

is a surface normal. Although it may not have unit length, using

it in formulas, as we shall do, rather than a normalized version will simplify expres-

sions but not change the validity of when certain dot products are zero.

Consider the meridian

and its derivatives

It is easy to check that

and so a(t) is a geodesic by the theorems mentioned.

Next, consider the circle of latitude

and its derivatives

This time

≤∑ ¥

()

¥¢

()

=¢FF

bq q q

()

() ()()

≤

()

()()

, sin , cos

, cos , sin .

yt yt

bq q

()

F t,

≤∑ ¥

()

¥¢

()

=FF

aqq

()

=¢

()

()()

≤

()

=≤

()

≤

()

≤

()()

txtyt yt

, cos , sin

aqtt

()

F ,

t t ytyt xt xt, , , cos , sin .qq q q

()

-¢

()

-¢

()()

9.10 Geodesics 629

meridian

h(t)=(x(t),y(t))

Figure 9.27. Geodesics on a surface of

revolution.

But y π 0 because the curve h(t) does not cross the x-axis, and so this expression will

vanish if and only if y¢=0. This is equivalent to saying that F

(t,q) = (x¢(t),0,0), which

is what we were trying to show.

As an application, consider the torus and its parameterization as deﬁned in

Example 9.9.18. We can think of this torus as a surface of revolution where the curve

gets revolved about the x-axis. It is clear that the meridians, which are circles in this

case, are geodesics. On the other hand, y¢(t) = cost = 0 implies that t =p/2 or 3p/2. In

other words, the only circles of latitude that are geodesics are the inner circle with

radius R - r and the outer circle with radius R + r.

Our deﬁnition of geodesic applied only to surfaces in R

because we made use

of the normal vectors to the surface. Obviously, the normal curvature of a curve

depends on having a normal vector, but it turns out that its geodesic curvature does

not.

9.10.10. Theorem. (Minding) The geodesic curvature of a curve in a surface is a

metric invariant.

Proof. Speciﬁcally, what we want to show is that the geodesic curvature depends

only on the curve and the metric coefﬁcients of the surface. How the surface is

imbedded in R

plays no role.

Let

be a regular one-to-one parameterization of a surface S in R

and let n(p) be the unit

normal vector to the surface S at the point p. Let

be a curve parameterized by arc-length. Express g in the form g(s) =F(m(s)),

where

Now

(9.69)

and

(9.70)

Substituting the right-hand side of equations (9.58) for the F

, F

, and F

in equa-

tion (9.70) gives

g≤= ¢ + ¢ ¢+ ¢ + ≤+ ≤FFFFF

uu uv vv u v

uuvvuv

g¢= ¢+ ¢FF

mm:, , .a b and s u s v s

[]

()

() ()()

g :,ab

[]

Æ S

F : USÆ

h t RrtrtrtRrtxtyt

()

() ()()

0, cos , sin cos , sin ,

630 9 Differential Geometry

so that equation (9.65) clearly implies that

To make the pattern more apparent, we change our notation slightly and rename our

parameters u and v to x

and x

, respectively, so that we can rewrite the last equation

using summation notation as

(9.71)

and F

are the partials F

and F

, respectively.) But, using Equation (9.69),

Therefore, if we let c

= n •(F

¥F

), then

Finally, since

we have shown that k

depends only on the Christoffel symbols, which are metric

invariants by equation (9.59), and g. The theorem is proved.

Moving on to property (2) of straight lines, we can see from Example 9.10.8 that

a geodesic in S

, as we have deﬁned one, can start at a point, go round and round a

great circle, and ﬁnally end up at that point again, so that it is not necessarily the

shortest curve between any two points. On the other hand, they do satisfy property

(2) locally. One can prove the following:

9.10.11. Theorem. Let S be a surface in R

. Let h:[a,b] Æ S be a regular curve.

(1) If h(t) is a geodesic, then there is an e>0 with the property that if |s

- s

<ethen g|[s

] is a curve of shortest length from g(s

) to g(s

(2) If h(t) is a curve of shortest length from h(a) to h(b), then h(t) is a geodesic.

c c and c c g

11 22 12 21

0== =-=,

gg k

ijkm

kkm

nn x xx n

xxxxc

()

∑= ¢¢+ ¢¢

∑

=¢¢+¢¢

ÂÂ

SS S

nn=¥¢= ¢ ¥

F .

ijk

nx xx

=¢¢+ ¢¢

ÂÂ

guv

nu u uv v v u uv v

=≤+ ¢+ ¢¢+ ¢

[]

+≤+ ¢+ ¢¢+ ¢

[]

GGGFGGGF

22.

g≤= ¢ + ¢ ¢+ ¢

[]

+≤+ ¢+ ¢¢+ ¢

[]

+≤+ ¢+ ¢¢+ ¢

[]

Lu Mu v Nv

uu uvv vu uvv

G G GF G G GF,

9.10 Geodesics 631

Proof. For a proof of (1) using the exponential map which is deﬁned later in this

section see [Thor79]. For (2) see [MilP77].

Theorem 9.10.11 implies that the ﬁrst deﬁnition of a geodesic is equivalent to the

following one:

Third deﬁnition of a geodesic: A geodesic on a surface S in R

is just a regular

curve in S that has the property that locally it deﬁnes a curve of shortest length.

Moving on to property (3) of straight lines, it is easy to give examples that show

geodesics are neither unique nor exist in general. For example, there are an inﬁnite

number of (in fact, minimal-length) geodesics between antipodal points on a sphere

and the surface R

-0 (a punctured plane) has no geodesic from (-1,0) to (1,0) (there

exist curves between the two points with length arbitrarily close to 2 but none of length

exactly 2). Although there may not be a geodesic between an arbitrary pair of points,

geodesics do exist if the points are not too far apart. The proof of this fact will also

show that ﬁnding geodesics is simply a matter of solving second order differential

equations.

9.10.12. Theorem. Let S be a surface in R

. Let p Œ S and v Œ T

(S), v π 0. Then

there is an e>0 and a unique constant speed geodesic g:(-e,e) Æ S with g(0) = p and

g¢(0) = v. (For v = 0, the unique “geodesic” would be the constant curve g(t) = p.)

Sketch of two proofs. For the ﬁrst proof, we use a regular parameterization F of

a neighborhood of p in S and equation (9.71). Since we are looking for a geodesic,

the left-hand side of the equation vanishes. But the partials F

and F

are linearly

independent, being a basis of the tangent space. It follows that any solution g must

satisfy the equations

(9.72)

Conversely, one can show that any such solution satisfying our initial conditions will

solve our problem, namely, it must be a constant speed curve. One only has to appeal

to theorems about the existence and uniqueness of solutions to differential equations

to ﬁnish the proof. See [MilP77].

The proof we just sketched shows that the existence of geodesics is an intrinsic

property of surfaces that does not depend on any imbedding in R

. The second proof

does use the imbedding and normals to the surface. Its advantage is that it is more

direct and useful computationally. In practice, surfaces are presented via parameter-

izations anyway, so computing normals is not a problem.

Near p one can represent the surface S as the zero set of some function, that is,

we may assume that

for some function f:U Æ R, where U is a subset of R

and the gradient of f does not

vanish on U. In this case, the Gauss map for S is given by

S =

()

¢¢ + ¢ ¢ = =

xxxk

,,.

012

632 9 Differential Geometry

Now, by Theorem 9.10.3(2), g is a geodesic if and only if

for some function a. It follows that

because g¢•(n  g) = 0. In other words, g is a geodesic if and only if

(9.73)

If n(p) = (n

(p),n

(p)) and g(t) = (x

(t),x

(t)), then solving equation (9.73)

reduces to solving the three second-order differential equations

(9.74)

The theorem now follows from theorems about solutions to such equations. See

[Thor79] for more details. In fact it is shown there that there is a maximal open inter-

val containing 0 over which the unique geodesic g(t) is deﬁned.

The form of the result in Theorem 9.10.12 leads to a natural question. Can one

extend the domain of the geodesic g in the theorem from (-e,e) to all of R?

Deﬁnition. A surface S is said to be geodesically complete if every geodesic g:(a,b)

Æ S extends to a geodesic :R Æ S.

9.10.13. Example. Neither the open unit disk nor R

- 0 is geodesically complete.

9.10.14. Theorem. (The Hopf-Rinow Theorem)

(1) A surface is geodesically complete if and only if it is complete in the topolog-

ical sense.

(2) If a surface is geodesically complete, then any two points can be joined by

minimal-length geodesics.

(3) In a closed and compact surface there is a minimal-length geodesic between

any two points.

Proof. See [Hick65] or [McCl97]. Part (2) implies part (3) because by Theorem 5.5.7

every compact metrizable space is complete.

Moving on to property (4) of straight lines, we ﬁrst need to deﬁne what it means

for a vector ﬁeld along a curve to consist of parallel lines. Let S be a surface in R

and let

nxx x

xxx

123

0123+

()()

,, ,, , ,,.

∂

gg g g≤+ ¢∑

()

()()

=nnoo0.

ag g g g g g g g=≤∑

()

=¢∑

()()

¢- ¢∑

()

=- ¢∑

()

¢nn n noo o o,

gag≤

()

() ()()

tttn

np p

()

—

()

9.10 Geodesics 633

be a curve.

Deﬁnition. A vector ﬁeld along the curve h is a function X:[a,b] Æ R

with the prop-

erty that X(t) is a vector tangent to S at h(t) for all t, that is, X(t) Œ T

h(t)

(S) for all t.

The vector ﬁeld X is said to differentiable if X(t) is a differentiable function.

Since the tangent space at a point of a surface is a vector space, it is easy to see

that the set of vector ﬁelds along a curve is a vector space. Let X(t) be a differentiable

vector ﬁeld along h(t). Although the vector X¢(t) is not necessarily tangent to the

surface at h(t), its orthogonal projection onto the tangent space obviously will be.

Deﬁnition. The covariant derivative of X(t), denoted by DX/dt, is the vector ﬁeld

along h which sends t Œ [a,b] to the vector that is the orthogonal projection of X¢(t)

on the tangent space of S at h(t). More precisely,

where n(h(t)) is a unit normal vector to S at h(t).

The deﬁnition of the covariant derivative does not depend on the choice of n(h(t)).

9.10.15. Theorem. Let X(t) and Y(t) be differentiable vector ﬁelds along h(t) and

let f:[a,b] Æ R be a differentiable function.

(1)

(2)

(3)

Proof. This is a straightforward computation of derivatives (Exercise 9.10.4).

Note that if S is a plane, then the covariant derivative is just the ordinary deriva-

tive of the vector ﬁeld. Intuitively, the covariant derivative of a vector ﬁeld just meas-

ures the rate of change of the vector ﬁeld as seen from “inside” the surface where one

does not have any notion of a normal.

Deﬁnition. We say that the vector ﬁeld X(t) on h(t) is parallel along h if dX/dt = 0,

that is, its covariant derivative vanishes.

One can easily show that if S is a plane, then the vector ﬁeld X(t) is parallel along

h if and only if X(t) is constant. We see that we seem to have found a generalization

of what it means for vectors to be parallel. It was Levi-Civita who introduced the

covariant derivative as a means of describing parallelism. As is pointed out in

∑

()

=∑+∑.

fff

()

=¢ + .

()

=+.

ttttt

XXnn

()

=¢

()

-¢

()

∑

()()()()()

hh,

h:,ab

[]

Æ S

634 9 Differential Geometry

[Stok69], the origin of the deﬁnition of parallel vector ﬁelds is closely related to devel-

opable surfaces, which are deﬁned in Section 9.15. The relevant property of these sur-

faces is that they can be isometrically embedded in the plane and Levi-Civita originally

deﬁned a vector ﬁeld to be parallel if it mapped to a parallel vector ﬁeld on the plane

under such a mapping. Of course not all surfaces are developable and Levi-Civita

reduced the general case to the developable case by constructing a developable surface

that was tangent to the given surface along the curve h.

Here are the important properties of parallel vector ﬁelds.

9.10.16. Theorem. Let S be a surface in R

and let h:[a,b] Æ S be a curve. Let X

and Y be differentiable vector ﬁelds along h.

(1) If X is parallel along h, then the vectors of X have constant length.

(2) If X and Y are parallel along h, then X •Y is constant along h.

(3) If X and Y are parallel along h, then the angle between the vectors of X and

Y is constant.

(4) If X and Y are parallel along h, then so are the vector ﬁelds X + Y and cX, for

all c Œ R.

Proof. Part (1) follows from Theorem 9.10.15(3) and the identities

Part (2) also follows from Theorem 9.10.15(3), which implies that the derivative of

X •Y vanishes since the covariant derivatives vanish. Part (3) follows from parts (1)

and (2) and the deﬁnition of angle between vectors. Part (4) is left as an easy exercise.

9.10.17. Theorem. Let S be a surface in R

. A constant speed regular curve h:[a,b]

Æ S is a geodesic according to our ﬁrst deﬁnition of a geodesic if and only if the

tangent vector ﬁeld h¢(t) is parallel along the curve.

Proof. A constant speed curve h has the property that h¢ and h≤ are orthogonal. In

this case the covariant derivative is just the geodesic curvature.

Theorem 9.10.17 leads to the next deﬁnition of a geodesic.

Fourth deﬁnition of a geodesic: A geodesic on a surface S in R

is just a regular

curve in S whose tangent vectors form a parallel vector ﬁeld along the curve.

Note that the new deﬁnition is equivalent to the second deﬁnition, but since it

applies (by Theorem 9.10.16(1)) only to constant speed curves it is technically not

equivalent to the ﬁrst and third deﬁnitions, which applied to arbitrary regular curves.

Overlooking this technicality, the reader may wonder why one bothers with a deﬁni-

tion of covariant derivative and parallel vector ﬁelds when in the end the new deﬁni-

tion of geodesic is basically the same as the one that is phrased in terms of geodesic

curvature. Well, the problem is that although geodesic curvature may seem like a rea-

sonable intuitive geometric concept, as we deﬁned it, it is not an intrinsic invariant

tXXX

()

∑

()()

=∑

()

20.

9.10 Geodesics 635

of the surface but seems to depend on the surface being imbedded in R

because we

used a normal vector to the surface. We shall see later in Section 9.16 that geodesics

really do not depend on any imbedding. In fact, they can be deﬁned for any manifold,

not just a surface, and depend only on the metric coefﬁcients. It is at that point of

abstraction that one sees why the preferred development of geodesics is via a global

notion of parallel vector ﬁelds and why the geodesic curvature is the secondary notion.

Of course, one will have to give a more intrinsic deﬁnition of parallel vector ﬁelds

since the deﬁnitions for the covariant derivative and parallel vector ﬁelds in this

section also depended on a normal vector.

As one ﬁnal point about parallel vector ﬁelds, we address the question of their

existence and uniqueness.

9.10.18. Theorem. Let S be a surface in R

and let h:[a,b] Æ S be a curve.

Let v Œ T

h(a)

(S). Then there exists a unique parallel vector ﬁeld X(t) along h with

X(a) = v.

Proof. The proof simply consists of analyzing the condition for a vector ﬁeld to be

parallel. The condition is equivalent to ﬁnding a solution to ﬁrst order differential

equations with initial condition v. See [Thor79].

An interesting consequence of the last theorem is

9.10.19. Corollary. Let S be a surface in R

and let g(s) be a geodesic in S. Then a

vector ﬁeld X along g is parallel along g if and only if both the length of all the vectors

of X and the angle between them and g¢(s) is constant.

Proof. See [Thor79].

Furthermore, since parallel vector ﬁelds are completely deﬁned by their initial

vector, one introduces the following useful terminology.

Deﬁnition. Let S be a surface in R

and let h:[a,b] Æ S be a curve. Let v Œ T

h(a)

(S).

Let X be the unique vector ﬁeld along h that satisﬁes X(a) = v. If c Œ [a,b], then X(c)

is called the parallel translate of v to h(c) along h.

We ﬁnish our introduction to geodesics on surfaces by deﬁning one more impor-

tant map. It turns out that one can rephrase the result in Theorem 9.10.12 as follows:

9.10.20. Theorem. Let S be a surface in R

. If p Œ S, then there is an e

> 0 so that

for all v Œ T

(S) with |v| <e

there is a unique geodesic g:(-2,2) Æ S with g(0) = p

and g¢(0) = v.

Proof. Exercise 9.10.5.

Using the notation in Theorem 9.10.20 let

Up v S v S

ppp

()

=Œ

()

{}

()

TTe

636 9 Differential Geometry

and deﬁne a map

See Figure 9.28.

Deﬁnition. The map exp

is called the exponential map of the surface S at p.

The exponential map is deﬁned in a neighborhood of the origin of each tangent

space. If the surface is geodesically complete, then the exponential map is deﬁned on

all of T

(S). The exponential maps exp

at points p deﬁne a map

that is also called the exponential map.

9.10.21. Theorem.

(1) Both exp

and exp are differentiable maps.

(2) The map exp

is a diffeomorphism of a neighborhood of the origin in T

(S)

onto a neighborhood of p in S.

(3) For each p Œ S and v Œ U(p), the unique geodesic g from p to q = exp

(v) is

deﬁned by

Proof. See [Thor79].

We see from Theorem 9.10.21 that the exponential map essentially formalizes the

concept of an “orthogonal projection” of a neighborhood of the origin in the tangent

space T

(S) to S.

g tt

()

exp .

exp:

open neighborhood of zero cross – section

in total space of tangent bundle t

exp exp

Up S v:.

()

by g 1

9.10 Geodesics 637

(S)

exp

(tv)

exp

(v)

Figure 9.28. The exponential map.

9.11 Envelopes of Surfaces

Although the concept of envelopes of surfaces was often used by geometers it is

actually tricky to deﬁne carefully. We shall simply extend the deﬁnition given in the

case of curves.

Deﬁnition. Let a

:[0,1] Æ R

be a one-parameter family of surfaces deﬁned by

for some C

•

function

An envelope of this family is deﬁned to be a surface p(u,v) that is not a member of

this family but that is tangent to some member of the family at every point.

Spivak ([Spiv75]) discusses the envelope of a family of planes. He shows that “in

general” a one-parameter family of planes has an envelope that is either a generalized

cylinder, a generalized cone, or the tangent surface of a curve. He also explains how

this led to a deﬁnition of parallel translation along a Riemannian manifold.

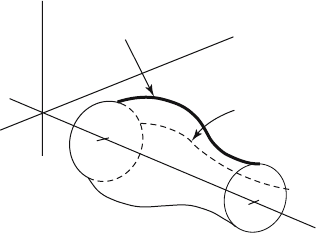
9.12 Canal Surfaces

This section is on a special type of envelope surface that is relevant to CAGD.

Deﬁnition. A canal surface is the envelope of a one-parameter family of spheres S(t).

If g(t) is the center of the sphere S(t), then the curve g(t) is called the center curve of

the canal surface. The function r(t), where r(t) is the radius of the sphere S(t), is called

the radius function of the canal surface. A canal surface whose radius function is con-

stant is called a tube surface.

Canal surfaces were ﬁrst deﬁned and studied by Gaspard Monge. If the center

curve for a canal surface is a straight line, then we get a surface of revolution. In

general, canal surfaces are a type of “sweep” surface. They are the boundary of the

solid that one gets by sweeping a sphere along a curve.

9.12.1. Lemma. If S(t) is the one-parameter family of spheres that deﬁnes a canal

surface S, then S(t) « S is a circle for every t.

Proof. This follows from the fact that S(t) « S is the limit of the intersections

S(t -d) « S(t +d) as d approaches 0.

Deﬁnition. The circles S(t) « S in Lemma 9.12.1 are called the characteristic circles

of the canal surface.

a :,,, .01 01 01

[]

Æ R

uv uvt,,,

()

638 9 Differential Geometry