Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics
Подождите немного. Документ загружается.

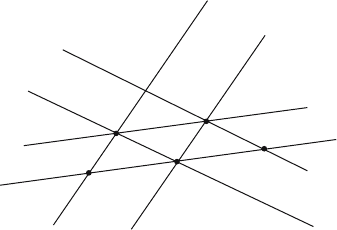
form A + rAB + sAC for all rational numbers r and s. These points are a dense set of
points in the plane. The final step handles the points where r or s are irrational. See
[Gans69].
2.4.7. Corollary. An affine transformation of the plane is completely determined by
what it does to three noncollinear points.
Proof. Showing that the corollary follows from Theorem 2.4.6 uses an, by now stan-
dard, argument that is left as an exercise for the reader.
We are ready to state and prove a fundamental theorem about affine maps.
2.4.8. Theorem. Every affine transformation of the plane can be described uniquely
by equations of the form (2.25). The determinant in (2.25b) is called the determinant
of the affine transformation. Conversely, every such pair of equations defines an affine
transformation.
Proof. We start with the converse. A transformation T defined by equations (2.25)
has an inverse that is again defined by linear equations of the same form. Let f(x,y)
= 0 be the equation of a line L. Then the set L¢=T(L) is defined by the equation
f(T
-1
(x,y)) = 0. This shows that L¢ is a line and that T is an affine map.
Next, let T be an affine map and choose three noncollinear points. By Theorem
2.4.5 there is a map M defined by equations (2.25) that agrees with T on those points.
Since we just showed that T is an affine map, we have two affine maps that act the
same on three noncollinear points. By Corollary 2.4.7, T = M and the theorem is
proved.
Because of Theorem 2.4.8 everything proved for the maps defined by equations
(2.25) holds for affine maps. We restate these properties to emphasize their validity
for affine maps.
(1) Every affine map in the plane is a composition of translations, rotations,
shears, and/or scaling transformations. Conversely, every composition of such
maps is an affine map.
(2) There is a unique affine transformation in the plane that maps three non-
collinear points into any other three noncollinear points.
2.4 Affine Transformations 99
A
B
C
D
E = A + 2AB
L
L
B
L
C
Figure 2.19. Proving Theorem 2.4.6.

2.4.9. Theorem. The only affine transformations of the plane that preserve angles
are similarities.
Sketch of proof. Let T be an affine transformation that preserves angles. Choose
noncollinear points A, B, and C. If T(A,B,C) = (A¢,B¢,C¢), then one can show that
for some r > 0. Let U be the radial transformation U(p) = (1/r)p and let (A≤,B≤,C≤) =
(UT)(A,B,C). There is a unique motion M such that (A≤,B≤,C≤) = M(A,B,C). Now S =
U
-1
M is a similarity that agrees with T on A, B, and C. By Corollary 2.4.7, T and S
must be the same transformations.
Definition. The ratio of division of three distinct points A, B, and P on an oriented
line L in R
n
, denoted by (AB,P), is defined by
(||AP|| and ||PB|| are the signed distances on the oriented line L.)
2.4.10. Proposition. Let A, B, and P be distinct points on an oriented line L. If
P = A + tAB = (1 - t)A + tB, then
In particular, (AB,P) is independent of the orientation of L.
Proof. See Figure 2.20. The proof is a straightforward consequence of the fact that
AP = tAB and PB = (1 - t)AB.
Using Proposition 2.4.10 it is easy to show that the ratio of division (AB,P) is
positive if P belongs to the segment [A,B] and negative otherwise.
2.4.11. Proposition. Let T be an affine transformation of the plane. If A,B ΠR
2
,
then
AB,P
()
=
-
t
t1
.
AB,P
AP
PB
()
= .
¢¢= ¢¢= ¢¢=A B AB B C BC A C ACr r and r,,
100 2 Affine Geometry
A
P
B
L
tAB
(1–t)AB
||AP||
||PB||
Figure 2.20. The ratio of division.
for all t.
Proof. By Theorem 2.4.8, there is a nonsingular 2 ¥ 2 matrix M and a point P,
so that T(Q) = QM + P for all Q. Now all one has to do is use this formula for T to
evaluate both sides of the equation and show that they are equal.
2.4.12. Theorem. Affine transformations of the plane preserve the ratio of division.
Proof. The theorem is an easy consequence of Propositions 2.4.10 and 2.4.11.
2.4.13. Theorem. Affine transformations in the plane multiply area by the absolute
value of their determinant.
Proof. See [Gans69].
Theorem 2.4.13 points out one of the main intuitions one should have about deter-
minants, namely, that they are intrinsically connected with how transformations
expand or shrink area, volume, etc. A precise definition of volume will be given in
Chapter 4.
Definition. The equiaffine or equiareal group is the group of affine transformations
with determinant ±1.
Recall our earlier comments how geometric properties are intimately connected
to certain groups of transformations. Here are three groups, the “metric” groups, and
their associated “metric” properties:
Definition. Affine properties are properties preserved only by affine transformations
(and not by projective transformations, which we will define shortly).
Some affine properties are betweenness, the ratio of division, parallelism, and the
concurrence of lines.
Definition. Two figures F and F¢ are affinely equivalent if there is an affine transfor-
mation T with T(F) = F¢.
Any two segments, angles, triangles, parallelograms, lines, parabolas, ellipses, and
hyperbolas are affinely equivalent. This means that one can use special simple figures
to prove things about general figures!
2.4.14. Example. To prove that the midpoints of all parallel chords of a parabola
X are collinear and lie on a line parallel to the axis. See Figure 2.21(a).
motions similarities equiaffine
distance angle size area
cc c
Ttt tT tT11-
()
+
()
=-
()()
+
()
AB A B
2.4 Affine Transformations 101

102 2 Affine Geometry
Solution. Since all parabolas are affinely equivalent we may restrict ourselves to the
special case of the parabola defined by the equation y = x
2
and the family of chords
determined by the lines y = mx + b, where m is fixed and b ≥ 0. See Figure 2.21(b).
To find the intersection of the lines with the parabola, we must solve the equation
mx + b = x
2
. The two solutions are
The midpoint Q = (u,v) of such a chord is defined by
and
which proves the result.
Finally, note that one could have developed affine geometry without first coordi-
natizing points. We could make points, lines, etc., undefined terms and use axioms to
define their properties. This is the synthetic geometry approach. Coordinates could be
introduced at a later stage. The point is that, in the context of affine geometry, the
exact lengths of geometric figures are not important. At most it is relative size that
counts, that is, the ratios of segments.
2.4.1 Parallel Projections
Definition. Let v be a nonzero vector in R
n
and let W be the family of parallel lines
with direction vector v. Let L
p
denote the line in W through the point p. If X is a
hyperplane in R
n
not parallel to v, then define a map
v
mx b mx b m b
=
++ +
=
+
12
2
2
2
2
,
u
xx m
=
+
=
12
22
x
mm b
and x
mm b
1
2
2
2
4
2
4
2
=
++
=
-+
.
midpoints
X
axis
parallel
chords
(a)
(b)
Q
y = x
2
y = mx + b
Figure 2.21. Midpoints of parallel chords for parabola are parallel to axis.
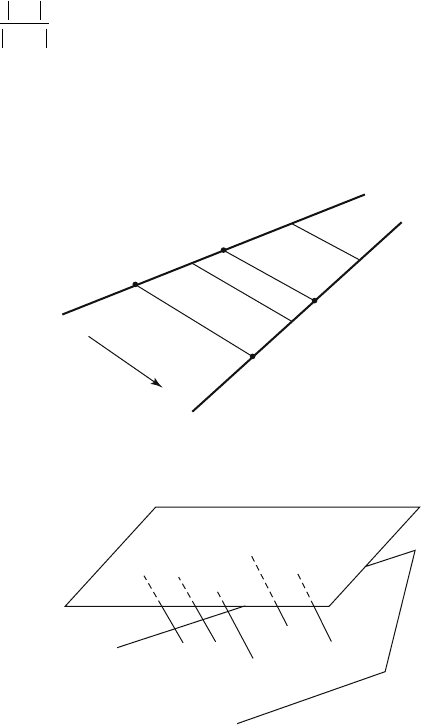
by
The map p
W
is called the parallel projection of R
n
onto the plane X parallel to v. If v is
orthogonal to X, then p
W
is called the orthogonal or orthographic projection of R
n
onto
the plane X; otherwise, it is called an oblique parallel projection. In general, if X and
Y are any subsets of R
n
, then the map that sends p in X to L
p
« Y in Y (wherever it
is defined) is called the parallel projection of X to Y.
Figure 2.22 shows a parallel projection of a line L onto a line L¢ and Figure 2.23,
a parallel projection of a plane X onto a plane X¢. Note that the ratio of distances is
preserved in the case of parallel projections of a line onto another line. What this
means is that, referring to Figure 2.22, the ratio
is independent of A and B. This is not the case for parallel projections of one plane
onto another. For example, in Figure 2.23 the ratios
AB
AB¢¢
p
W
pL X
p
()
=«.
p
W
: RX
n
Æ
2.4 Affine Transformations 103
A
v
A¢
B¢
L¢
B
L
L
A
L
B
A
C
B
X
X¢
B¢
C¢
A¢
Figure 2.22. A parallel projection between
lines.
Figure 2.23. A parallel projection between
planes.

are probably not the same.
2.4.1.1. Example. To find the parallel projection T of R
3
onto the plane X defined
by the equation
parallel to v = (3,1,1).
Solution. Clearly, given a point p, if t is chosen so that p + tv belongs to X, then
T(p) = p + tv. Let p = (x,y,z). Solving
for t, gives t = (1/2) (-x + 2y - z). It follows that T is defined by the equations
2.4.1.2. Theorem. A parallel projection between two hyperplanes in R
n
preserves
parallelism, concurrence, betweenness, and the ratio of division.
Proof. Easy.
2.4.1.3. Theorem. Any map of the plane onto itself that is a composition of
parallel projections is an affine map. Conversely, every affine map in the plane is a
composite of parallel projections.
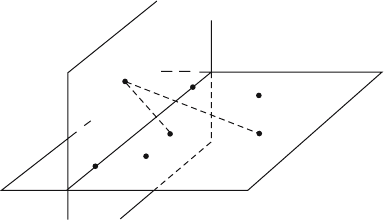
Sketch of proof. The first statement follows from the fact that lines are preserved.
Now let T be an affine map. Assume that A, B, and C are noncollinear points with
T(A,B,C) = (A¢,B¢,C¢). First, project R
2
to a plane X that contains A and B so that C
gets sent to a point C
1
. Next, project X back to R
2
in such a way as to send C
1
to C¢.
It follows that the composite of these two projections sends A to A, B to B, and C to
C¢. Repeat this process on A¢ and B¢. See Figure 2.24.
The construction in the proof of Theorem 2.4.1.3 shows that any affine map can
be realized as a composite of at most six projections.
¢=-+++zxyz
1
2
1
2
3
2
.
¢=-+-+yxyz
1
2
2
1
2
3
2
¢=-+-+xxyz
1
2
3
3
2
9
2
xt ytzt+
()
-+
()
++
()
=32 3
xyz-+=23
AB
AB
BC
BC¢¢ ¢¢
and
104 2 Affine Geometry
2.5 Beyond the Plane
Up to now, although some things applied to R
n
, most of the details were specifically
about transformations in the plane. The fact is that much of what we did generalizes
to higher dimensions.
We start with motions of R
n
.
2.5.1. Theorem. Every motion M:R
n
Æ R
n
can be expressed by equations of the
form
(2.29)
where A
M
= (a
ij
) is an orthogonal matrix. Conversely, every such system of equations
defines a motion.
Proof. The discussion in Section 2.2.8 on frames showed that the theorem is valid
for motions in the plane. For the general case, assume without loss of generality that
M(0) = 0. The key facts are Theorem 2.2.4.1, which says that M is a linear trans-
formation (and hence is defined by a matrix), and Lemma 2.2.4.3, which says that
M(u)•M(v) = u • v, for all vectors u and v. The rest of the proof simply involves ana-
lyzing the conditions M(e
i
)•M(e
j
) = e
i
•e
j
=d
ij
and is left as an exercise (Exercise 2.5.1).
In studying motions in the plane we made use of some important special motions,
such as translations, rotations, and reflections. Translations already have a general
definition. The natural generalization of the definition of a reflection is to replace lines
by hyperplanes.
Definition. Let X be a hyperplane in R
n
. Define a map S:R
n
Æ R
n
, called the reflec-
tion about the hyperplane X, as follows: Let A be a point in X and let N be a normal
◊◊ ◊ ◊ ◊
¢= + + + +xaxax axc
nn n nnn
n
11 2 2
...
¢= + + + +
¢= + + + +
◊◊ ◊ ◊ ◊
xaxax axc
xaxax axc
nn
nn
1 11 1 12 2 1 1
2 21 1 22 2 2 2
...
...
2.5 Beyond the Plane 105
X
A
C
B
B¢
C¢
A¢
R
2
C
1
Figure 2.24. Affine maps as composites
of parallel projections.

106 2 Affine Geometry
vector for X. If P is any point in R
n
, then S(P) = P + 2PQ, where PQ is the orthogo-
nal projection of PA on N. See Figure 2.25.
2.5.2. Theorem. Let S be a reflection about a hyperplane X.
(1) The definition of S depends only on the hyperplane and not on the point A
and normal vector N that are chosen for it in the definition.
(2) If t is chosen so that P + tN is the point where the line through P with direc-
tion vector N meets the plane X, then S(P) = P + 2tN.
(3) The fixed points of S are just the points of X.
(4) If L¢ is a line orthogonal to X, then S(L¢) = L¢.
(5) Reflections about hyperplanes are motions.
Proof. The details of the proof are left as an exercise for the reader because it is
essentially the same as the proof of Theorem 2.2.3.1. That proof did not really use the
fact that vectors were two-dimensional.
2.5.3. Example. To find the reflection S about the plane X defined by the equation
Solution. Let A be any point in X. Since N = (1,-2,-2) is a normal vector for
X, if P is any point, then it is easy to show that the orthogonal projection of
PA on N is just tN, where t is chosen so that P + tN lies in X. Let P = (x,y,z).
Solving
for t, gives
t = (1/9)(-x + 2y + 2z + 3).
Since S(P) = P + 2tN, it follows that S has equations
xt y t z t+
()
--
()
--
()
=22223
xyz--=223.
A
N
P
X
Q
P¢
Figure 2.25. Defining a reflection in
higher dimensions.
Generalizing the concept of a rotation is a little less obvious. The simplest way to
get a definition is in a roundabout way by defining a rigid motion first and then use
the orientation-preserving nature of these maps.
Definition. Let M be a motion of R
n
and suppose the equations for M are as shown
in Theorem 2.5.1. The motion M is said to be a rigid motion if the matrix (a
ij
) is a
special orthogonal matrix.
In analogy to the planar case we get
2.5.4. Theorem. A rigid motion of R
n
is an orientation-preserving map. Conversely,
every orientation-preserving motion of R
n
is a rigid motion.
Proof. Exercise.
Definition. A rigid motion R of R
n
that fixes some point p is called a rotation. In
that case, we say that R is a rotation about p. The point p is called a center of the
rotation.
Is this definition of a rotation really what we want and does it generalize the intu-
itively simple notion of a rotation in the plane? Theorem 2.2.6.9 certainly shows that
the new definition is compatible with the old one.
2.5.5. Theorem. (The Principal Axis Theorem) Every rotation R in R
3
is a “rotation
about some line.” More precisely, with respect to some appropriate coordinate system,
R is just the rotation about the z-axis through an angle q, that is, the equations for R
in that coordinate system are just
(2.30)
In general, if R is a rotation in R
n
, then we can choose a coordinate system
with respect to which the n ¥ n matrix of coefficients in the equation for R has the
form
¢=zz.
¢= +y x in y osscqq
¢= -xx ycos sinqq
¢= - + -zxyz
4
9
8
9
1
9
4
3
.
¢= + - -yxyz
4
9
1
9
8
9
4
3
¢= + + +xxyz
7
9
4
9
4
9
2
3
2.5 Beyond the Plane 107
108 2 Affine Geometry
Conversely, every transformation of R
n
whose equation has such a matrix of coeffi-
cients is a rotation.
Proof. See [Lips68]. Note that rotations about the origin are linear transformations
so that one can talk about their associated matrices.
Theorem 2.5.5 suggests that the expression “rotation about a point” is perhaps
misleading in higher dimensions. Although it might be better to say “rotation about
a line,” we shall keep it in order to have a uniform terminology since it makes per-
fectly good sense in the plane. Actually, we shall see shortly in the next section that
one should really talk about directed lines here because the expression “rotation about
a line through an angle q” is ambiguous.
The main theorems about motions in R
n
can now be stated. Their proofs are very
similar to the proofs of the corresponding theorems about motions in the plane and
are omitted.
2.5.6. Theorem.
(1) A motion in R
n
is completely determined by what it does to n + 1 linearly inde-
pendent points.
(2) A rigid motion in R
n
is completely determined by what it does to n linearly
independent points.
(3) Every motion in R
n
can be described as a composition of a translation, a rota-
tion about the origin, and/or a reflection.
(4) Every rigid motion in R
n
is a composition of a translation and/or a rotation
about the origin.
Proof. Exercise.
Facts about similarities and affine maps in the plane also generalize to R
n
.
2.5.7. Theorem. Every similarity transformation can be expressed by equations of
the form (2.29) where (a
ij
) = (db
ij
), d > 0, and (b
ij
) is an orthogonal matrix. Conversely,
every such system of equations defines a similarity.
Proof. Exercise.
cos s
s cos
cos sin
sin cos
11
11
kk
kk
qq
qq
qq
qq
-
-
±
±
Ê
Ë
Á
Á
Á
Á
Á
Á
Á
Á
Á
Á
ˆ
¯
˜
˜
˜
˜
˜
˜
˜
˜
˜
˜
in
in
0
1
01
O
O
(2.31)
