Adlard E.R. (ed.) Chromatography in the Petroleum Industry
Подождите немного. Документ загружается.


I12
Chapter
4
In the theory section, the dimensionless Fourier number
Fo
=
D,t/R2
was in-
troduced.
Fo
can be interpreted as the number of times a particle moves through
the column cross-section during the time
t
of the chromatographic process. If
Fo
is much smaller than
1,
it means that a particle that
is
introduced at a given radial
position in the column virtually stays on the same velocity line all the time.
Thus, particles introduced at the exact centre of the column elute at a velocity
twice as high as the average velocity, while particles introduced near the column
wall, where the velocity is close to zero, elute only after a very long time. Under
these conditions one, of course, cannot expect to make any useful separation. In
our practical applications we have found that
Fo
1
10 is sufficient to ensure a
sufficiently high rate of radial mass transfer.
Now, when can we expect that this insufficient diffusion and
so too low a
Fourier number will occur?
As
an example, we have calculated
Fo
for
a number
of column and particle size combinations. The data, tabulated in Table
4.3,
per-
tain to a column length of
300
cm, an analysis time of
20
min and polystyrene in
THF,
eluting at
t
=
0.90.
We see from Table
4.3
that for a column somewhere between
10
and
30
pm
in
diameter, the Fourier number
will
become smaller than
10.
In
the l00pm col-
umn,
Fo
is even lower than
1,
albeit for the analysis of a polystyrene of ex-
tremely high molecular mass. But even with polystyrenes of lower molecular
mass, the Fourier number will
be
low, since the numerical value of the Fourier
number
is
largely determined
by
the
R2
term
in
the denominator of
Fo.
If we take
the case of a polystyrene with a molecular mass of
3.8
X
lo6
Da
(Fo
=
3500
in a
3
pm
column), this polymer would only have a
Fo
=
3
in
a l00pm diameter col-
umn (now of course with a larger value
for
the relative residence time;
t
=
0.996
instead of
0.90).
In
the literature on capillary
HDC,
one often encounters columns as wide as
500
pm,
in
which particles of e.g.
25
pm
diameter are separated in a few min-
utes. However, these large particles which have a very low diffusion coefficient,
are eluted under conditions in which
Fo
Q
1.
Separation is still established be-
tween particles of different diameter, but it will be clear that
Eq.
(4.7)
is not
TABLE
4.3
Fo
FOR
DIFFERENT COLUMNPARTICLE SIZE COMBmATIONS
Column
diameter
Molecular
mass
Diffusion coefficient
Fo
Pm)
(Dax
10”)
((cm2/s)
x
lo9)
3
3.8
67
3500
10
29
21
102
30
190
7.4
3.9
100
1500
2.3
0.1
Hydrodynamic chromatography
of
polymers
I13
applicable to these separations. Therefore, another mechanism must be respon-
sible for the separation in these wider-bore
HDC
capillaries. This only partly
understood phenomenon, called tubular pinch, is thought to consist of
two
op-
posite forces that work on particles with not too small an aspect ratio, which are
transported under conditions of a high reduced velocity ReSc. One
of
these
forces moves the particles away from the wall region; the other force transports
the particles away from the column centre. The net effect
is
that the particles are
concentrated into an annulus at
a
certain radial distance from the column centre,
the position of which depends, among other factors, upon the aspect ratio and the
reduced velocity. For a more extensive treatment, the reader is referred to Ti-
jssen and
Bos
[29].
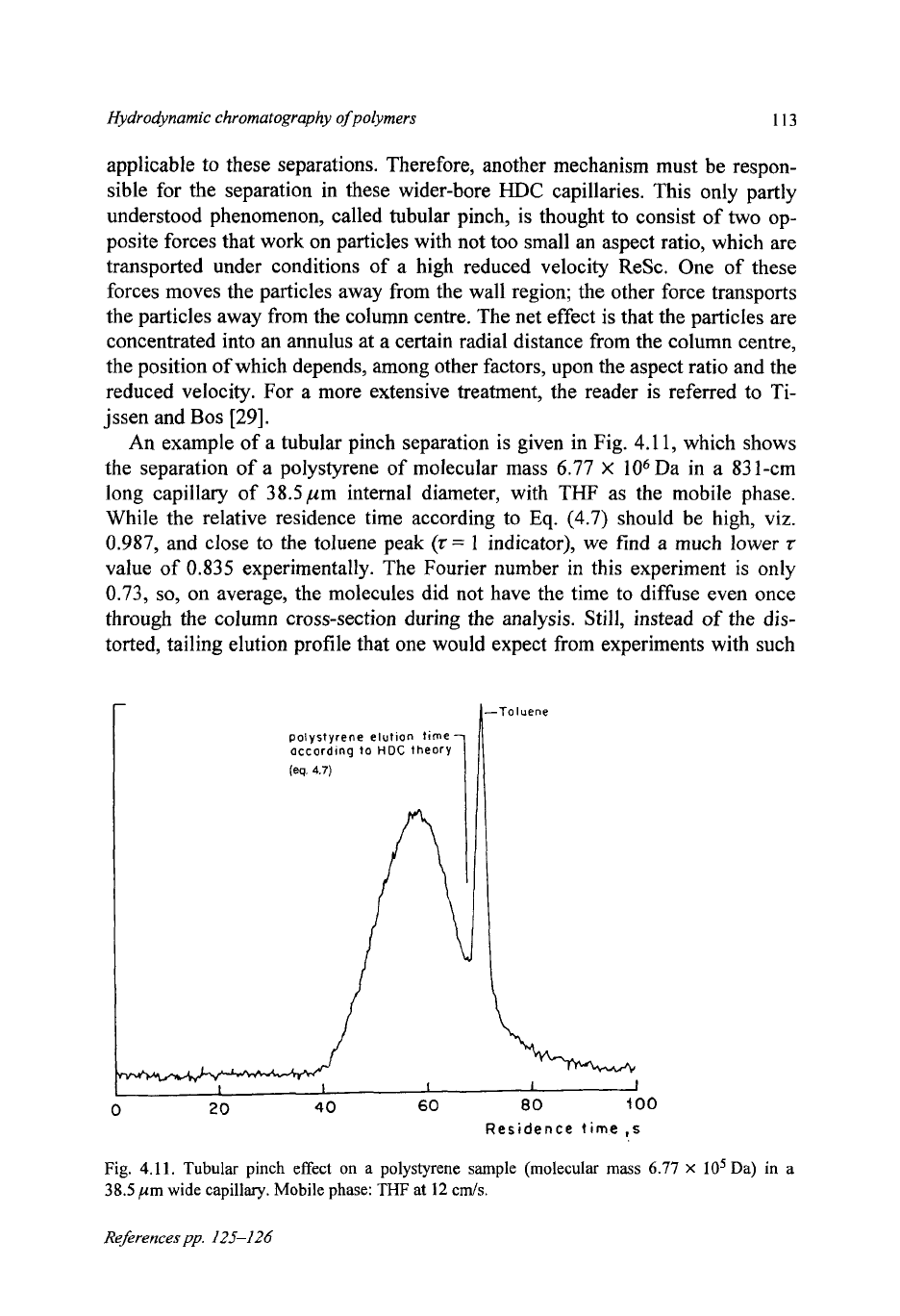
An example of a tubular pinch separation is given in Fig.
4.1
1,
which shows
the separation of a polystyrene of molecular mass
6.77
X
lo6 Da in a
83
1-cm
long capillary of 38.5pm internal diameter, with
THF
as the mobile phase.
While the relative residence time according to
Eq.
(4.7)
should be high, viz.
0.987, and close to the toluene peak
(z=
1
indicator), we find a
much
lower
t
value of 0.835 experimentally. The Fourier number in this experiment is only
0.73,
so,
on average, the molecules did not have the time to diffuse even once
through the column cross-section during the analysis. Still, instead
of
the dis-
torted, tailing elution profile that one would expect from experiments with such
polystyrene elution time
according to
HDC
theory
(eq.
4.7)
-Toluene
I
I
I
I
I
I
0
20
40
60
80
100
Residence
time
,s
Fig.
4.11.
Tubular pinch effect
on
a polystyrene sample [molecular
mass
6.77
x
lo5
Da)
in
a
38.5
pm wide capillary. Mobile phase:
THF
at
12
cds.
References
pp.
125-126

114
Chapter
4
a
low
Fourier number, the tubular pinch effect gives rise to a reasonably sym-
metrical peak form.
We introduce
8
as the reduced relative residence time:
6=
t(
experimental)
t(according to
Eq.
(4.7))
as
the relative measure for the tubular pinch effect. If
8
=
1,
then the experiment
is
in
agreement with
Eq.
(4.7),
and no tubular pinch effect is present. In the ex-
periment mentioned above, we find a reduced relative residence time
8
=
0.835/0.987
=
0.846.
Experimentally we find that, for fixed values of the
linear velocity and the column diameter,
8
is inversely proportional to the mo-
lecular mass of the eluted species; at fixed values
of
the molecular mass and the
column diameter
8
is inversely proportional to the linear velocity of the mobile
phase. Dimensional analysis reveals that
8
should be a function of the dimen-
sionless numbers Re, Sc and
I.
such that
8
=f(ReScA2)
(4.13)
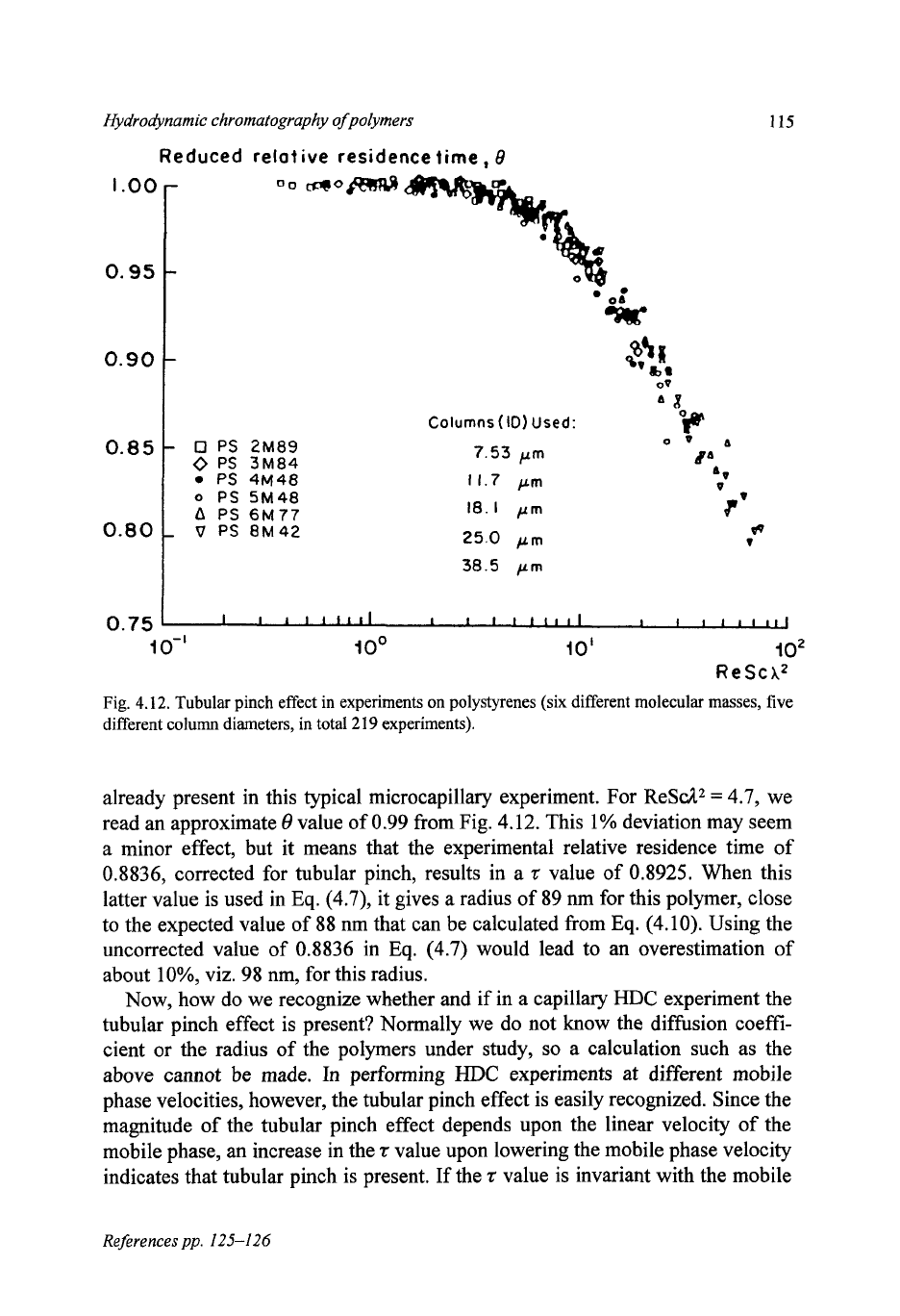
In Fig.
4.12,
a plot of
8
versus ReSd* is presented
for
219
experiments, in-
volving six polystyrenes (molecular masses
2.89
X
106-8.42
X
lo6
Da) in five
columns of different internal diameter
(7.53-38.5
pm), with
THF
as the mobile
phase. Column lengths varied between
200
and
835
cm, with mobile-phase linear
velocities ranging between
0.3
and
14
cm/s. The columns were used in
a
straightened out horizontal position to avoid curvature effects (see Section
4.3.2).
We see that all the measurements lie close to a single curve, indicating
that
Eq.
(4.13)
is
valid, although the exact form of the function
f
is still not
known (see, however,
[29]).
From Fig.
4.12,
we conclude that for
Eq.
(4.7)
to be
valid. a capillary HDC experiment must be conducted under conditions such that
ReSd2
5
1
(4.14)
At
ReSd2
>
6,
the functionfhas a high negative slope
so,
especially in that re-
gion,
estimation of the particle size from a measured relative residence time
t
alone, will lead to large errors.
It
is
stressed that tubular pinch effects are not necessarily found only in wide-
bore capillaries with high linear velocities. Even in microcapillary
HDC,
the ef-
fect can be found. For example, let
us
go back to Fig.
4.5,
which shows the ex-
periments
in
a 323-cm long column with radius
1.342,um.
The datapoint farthest
to the left stems from a polystyrene of molecular mass
3.61
X
lo6
Da, that is
eluted
in
THF
at
a
linear velocity of
0.28
cds. Using
Eqs.
(4.10)
and
(4.1
l),
we
can calculate a ReScjZ2 value of
4.7,
indicating that the tubular pinch effect is
Hya'roa!ynamic chromatography ofpolymers
Reduced relative residence
time,
6
115
0.90
0.85
0.80
-
0
PS
2M89
0
PS
3M84
0
PS
4M48
o
PS
5M48
A
PS
6M77
-
V
PS
8M42
$5
R
%r
09
Columns
(10)
Used:
00
d
7.53
pm
11.7
pm
18.1
pm
25.0
pm
v-
?v
VQ
T
38.5
prn
0.75
I
I
1
I1
IlII
I
I
I
I1
1111
1
I
1
I
Illlj
lo-'
loo
10'
lo2
ReSCX2
Fig.
4.12.
Tubular pinch effect in experiments on polystyrenes (six different molecular masses, five
different column diameters, in total
2
19
experiments).
already present in this typical microcapillary experiment. For ReSd2
=
4.7,
we
read an approximate
8
value of 0.99 from Fig. 4.12. This 1% deviation may seem
a minor effect, but
it
means that the experimental relative residence time of
0.8836, corrected for tubular pinch, results in a
z
value of 0.8925. When this
latter value is used in
Eq.
(4.7), it gives a radius of 89 nm for this polymer, close
to the expected value of 88 nm that can be calculated from
Eq.
(4.10). Using the
uncorrected value of 0.8836 in
Eq.
(4.7) would lead to an overestimation of
about lo%, viz. 98 nm, for this radius.
Now, how
do
we recognize whether and if in a capillary
HDC
experiment the
tubular pinch effect is present? Normally we do not know the diffusion coeffi-
cient or the radius of the polymers under study,
so
a calculation such as the
above cannot be made. In performing
HDC
experiments at different mobile
phase velocities, however, the tubular pinch effect is easily recognized. Since the
magnitude of the tubular pinch effect depends upon the linear velocity of the
mobile phase, an increase in the
z
value upon lowering the mobile phase velocity
indicates that tubular pinch is present. If the
z
value is invariant with the mobile
References pp.
125-126

I
I6
Chapter
4
phase velocity, then the experiment has been conducted under conditions such
that no tubular pinch occurs and Eq. (4.7) is valid.
If the
HDC
experiment
is
an old one that we cannot or
do
not want to repeat,
or
if we examine experiments from the literature, we still can make an estimate if
tubular pinch effects have
not
been present.
To
that end, we calculate the appar-
ent molecular radius
r’
using the experimental
t
value in Eq. (4.7). If tubular
pinch effects are present,
t
values are shifted towards lower values, and the cal-
culated radius will be over-estimated,
so
r’
>
F.
From
r’,
we calculate the appar-
ent molecular diffusion coefficient
D,’
from the StokesEinstein equation
(4.15)
where
k
is
the Boltzman number (1.38
X
1
0-l6
g cm2/s2
K)
and
T
is
the absolute
temperature
(K).
Since r’is over-estimated,
D,’
will be smaller than the true, un-
known
D,.
As
the Stokes/Einstein equation
is
in fact only valid for spherical
solid particles, application of Eq. (4.15) to
a
macromolecular coil will, in that
case, give an even lower apparent diffusion coefficient (compare e.g. Eqs. (4.10)
and (4.1 1) with Eq. (4.15) for polystyrene in
THF
to see this effect).
Also,
A’
=
r‘/R
will be higher than the true aspect ratio
A
=
r/R.
Taking all this into
account, the apparent value (ReSd2)’ will be larger than the true value for
ReSd’. Only if (ReSd2)’
<
1 can we be sure that there was no tubular pinch ef-
fect in the experiment.
As
an example, let us calculate this for the polystyrene of molecular mass
3.61
X
lo6
Da that was mentioned earlier as an example of tubular pinch in
a
microcapillary
HDC
experiment (datapoint farthest to the left in Fig. 4.5). From
the uncorrected relative residence time
z
=
0.8836, we found the apparent radius
of
98 nm. From this, the apparent diffusion coefficient of
D,’
=
4.51
X
1
0-8
cm2/s
is
calculated according to Eq. (4.1 5) (with 0.00488
P
for the viscosity
at 22°C). With 0.28 cm/s for the linear velocity and an internal radius of
1.342pm for the column, we calculate that (ReSd2)’
=
8.9.
Since this value
is
larger than 1, the experimental value for
t
is suspect; tubular pinch may well
have been present, although we do not know if the real ReSd2 value is also lar-
ger than
1
(earlier,
for
this specific case, we calculated that ReSd2
=
4.7,
is
in-
deed larger than
1
,
using the exact
F
and
D,
values from Eqs. (4.10) and (4.11)).
If we take the lowest
left
data point
in
Fig. 4.5, with
a
relative residence time
t
=
0.9823, we can calculate that (ReSd2)‘= 0.017. This value is
so
much
smaller than
1
that there will have been no tubular pinch effect in the experi-
ment. Thus, it is permissible to use Eq. (4.7)
to
calculate the radius from the
relative residence time. This is, of course, confirmed by the result for this poly-
styrene of molecular mass 1.27
X
lo5 Da, that has already been presented in
Table 4.2.
Hydrodynamic chromatography ofpolymers
117
As
a last remark on this subject, we want to point out that, although tubular
pinch has been identified as a separating mechanism that can operate at low
Fourier numbers, this does not mean that the tubular pinch effect is therefore
absent at high Fourier numbers.
In
our experiments leading to the construction of
Fig.
4.12,
sometimes Fourier numbers in excess of
200
could be calculated. This
means that there is a rapid radial mixing of the polymer through the available
column cross-section, but still the relative residence time was lower than it
should have been according to Eq.
(4.7).
Consequently, tubular pinch is a rela-
tively strong effect, that can accumulate molecules into an annulus at a certain
radial position in a column, even when opposed by counteracting diffusion or
dispersion mechanisms that would tend to re-distribute these molecules through-
out the whole available cross-section.
4.3.2
Coiling
effects
With the columns used to establish the
8
versus ReSd2 graph in Fig.
4.12,
it
is possible to separate polystyrenes with different molecular masses, using the
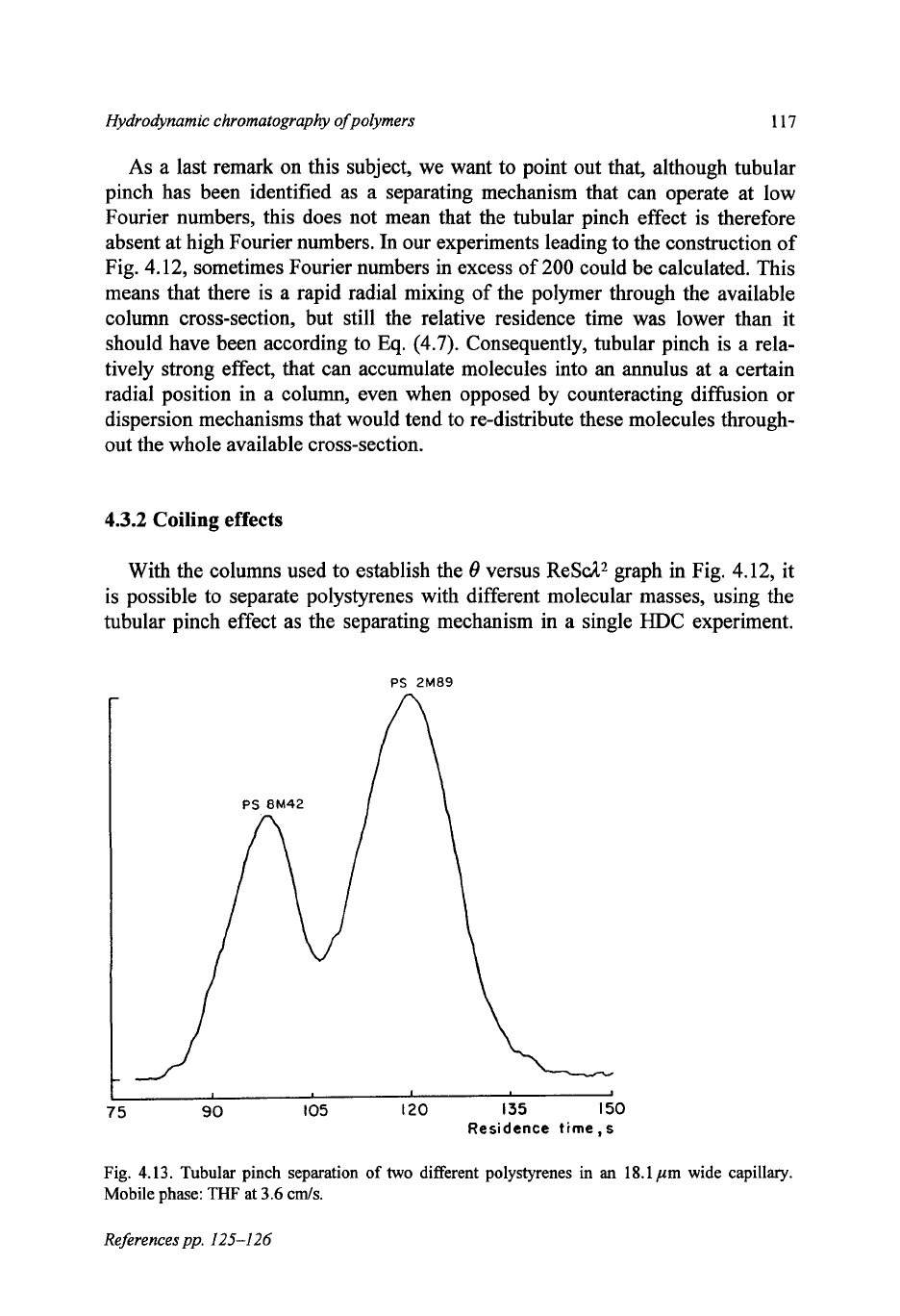
tubular pinch effect as the separating mechanism in a single HDC experiment.
PS
2M89
I
I
I
I
75
90
105
I20
I35
I50
Residence
time,
s
Fig.
4.13.
Tubular pinch separation
of
two
different polystyrenes in
an
18.1
pm
wide capillary.
Mobile phase:
THF
at
3.6
cds.
References pp.
125-1
26

118
Chapter
4
An example of this
is
given in Fig.
4.13
for a mixture of
two
polystyrenes with
molecular masses of
8.42
X
1
O6
and
2.89
X
1
O6
Da in a column of
18.1
pm in-
ternal diameter, using
THF
as
the mobile phase at a linear velocity of
3.6
cds.
From the relative residence times
(0.80
and
0.97),
determined in
a
run in which
toluene had been added
as
the
t
=
1
indicator, it is easy to calculate that the sepa-
ration mechanism in this experiment
is
due to tubular pinch, since (ReSd2)’ is
much larger than
1
for these peaks
(5
X
lo4
and
52,
respectively). Also, since in
this case we know the exact size of these polymers
(Eq.
(4.10)),
it can be pre-
dicted that a
HDC
separation without tubular pinch would produce peaks that
would hardly be separated at all (relative residence times
0.97
and
0.98).
Al-
though the separation
is
still incomplete, it should be noted that
two
polymers of
rather high molecular mass have been separated in less than
2.5
min.
It
is
clear that the chromatographic spreading of the polymers must be dimin-
ished to make such a separation more useful.
To
attain this, coiling of the
HDC
column could potentially be of importance.
As
mentioned earlier, coiling distorts
the Poiseuille profile, an effect that becomes notable when the dimensionless
quantity Re2Sd, is larger than
50.
Coiling has the effect of increasing the radial
Toluene
Cotled column
.
.
.
.
. .
. . .
Straight
column
I
I
1
40
56
72
88
I04
120
Residence
time
,
s
Fig.
4.14.
Effect
of
column coiling on
the
width
of
the elution profile
of
a polystyrene
of
molecular
mass
3.84
X
lo6
Da
in
a
38.5pm
wide capillary. Mobile phase:
THF
at
9.7
cds. Coil diameter
6.3
cm.

Hydrodynamic chromatography ofpolymers
119
mixing in the column, which shows up as a narrowing of the chromatographic
zones [30]. An example of this is shown in Fig. 4.14 for a polystyrene of molecu-
lar mass 3.84
X
lo6
Day transported at a linear velocity
ii
=
9.7 cm/s through a
83 1-cm long capillary with an internal diameter of 38.5 pm.
In
a straight column,
the polymer elutes at
z
=
0.93, showing that there is a tubular pinch effect
((ReSd2)’
=
8000,
ReSd2
=
13). The peak has a standard deviation of
(T
=
10.6
s.
When the experiment is repeated, but now with the column coiled (coil
diameter 6.3 cm), the polymer elutes at the same relative residence time, but it is
distinctly narrower with
(T
=
7.5
s.
In
this last experiment, Re2Sd,
=
2300.
In a number of experiments in this coiled column with polystyrenes of other
molecular mass, we invariably found that the relative residence times were the
same as in the straight column. Thus tubular pinch concentrates the polymer in
an annulus in the column, and the strong secondary flow introduced by coiling is
unable to redistribute the molecules through the available column cross-section.
However, the increased radial transport of the molecules within the annulus
leads to a reduced chromatographic band spreading.
To
diminish the band spreading to such an extent that the polymers in Fig.
4.13 are baseline separated would require much higher Re2ScA-, numbers. This
implies higher linear velocities in a longer column that is more tightly wound.
With the fused silica column used in the experiment of Fig. 4.13, this is impos-
sible, since the required pump pressure would be too high. Also, fused silica
capillaries cannot be wound in a very tight coil. With the wider metal and Teflon
columns that have been reported in the literature, this poses no problem,
so
in
those cases the best separations can be expected with tightly coiled columns that
are operated at the highest possible mobile-phase linear velocity.
4.3.3
Applications
Almost all the applications that are found in the field of capillary
HDC
are
separations of particles, e.g. latex, pollen, garnet, paper fibres, bacterial spores,
silica, paints, etc. The diameters of the capillaries used span a wide range of in-
ternal diameters (14-500pm).
In
the separation of paper fibres even a column
with an internal diameter of 15 mm has been used, which shows that the term
“capillary” is a rather flexible description. This wide range in column diameters
leads to various instrumental designs, where the small internal diameter experi-
ments are carried out in an instrument like the one described in Section 4.2.3 on
microcapillary
HDC,
while with larger internal diameter columns, standard
HPLC
injection and detection techniques can be used. Normally ultraviolet ab-
sorption is used as the detection technique, although Zarrin and Dovichi [33] use
a sheath flow cuvette with a light-scattering detector.
References pp.
125-126

120
Chapter
4
The applications that describe separations of polymers are rare. Revillon and
Boucher
[34]
separated a cross-linked polystyrene sample in
THF
in a 120-m
long capillary of 250pm internal diameter. Brough
et
al.
[12] applied a 50-m
long, 242pm internal diameter column to separate a used engine oil into two
peaks, one of which was due to particulate debris such as carbon, metals and
polymeric products. They also analysed a THF solution of a water-based emul-
sion paint on a 50-m long, 450pm internal diameter column to “fingerprint”
successive batches of paint. Especially in the case of the analysis of the used
engine oil, we feel that the separation between the two peaks could have been
improved if a much smaller coil diameter than the reported
30
cm had been used.
Tazaki and Homma
[35]
used a stainless steel column
(90
m long, 250pm inter-
nal diameter) and a fused silica column (25
m
long, 100pm internal diameter)
for the separation
of
fluorescence-tagged xanthane polysaccharides in water and
aqueous buffers.
As there
is
no possibility of calculating molecular dimensions
from the relative residence time alone, when tubular pinch
is
present, Tazaki ex-
presses the size as the “equivalent particle diameter”, i.e. the diameter of a poly-
styrene latex particle that would have eluted at the same relative residence time.
He states that his result,
330
nm, is in good agreement with the HDC experi-
ments in packed columns of Prud’homme and Hoagland
[36]
who found a value
of
150-300
nm.
In summary, examples
of
polymer separations in capillary HDC are not abun-
dant. Still, we feel that the method has potential for the characterization of high-
molecular-mass materials that are difficult
to
handle in
GPC
or
packed-column
HDC.
For efficient separations
in
packed columns, we have to use column
packing materials of small size, e.g.
3-5
pm particles. Since these packings are
retained in the column by still finer metal frits of e.g. OSpm, high-molecular
species tend to be “filtered off” on these frits.
In
addition, mechanical degrada-
tion of the polymers can take place in the frits
or
in the injection system, where,
to
ensure a
good
injection quality, the injection pulse is transported at a very
high linear velocity through narrow-bore tubes before entering the region
of
lower linear velocities
in
the wider-bore chromatographic column. With capil-
lary
HDC
there are no frits through which the polymers have to pass and the in-
jection can be made with good efficiency, without subjecting the polymers to
excessively high linear velocities. Yet, the absence of detectors (other than
UV
absorbance) that can be used in narrow-bore capillaries is a serious drawback in
the capillary HDC technique.
4.4
HYDRODYNAMIC
CHROMATOGRAPHY
IN
PACKED
COLUMNS
The packing material
in
column
HDC
consists,
in
general,
of
spherical, im-
permeable spheres
of
e.g. glass, silica
or
ion-exchange resin. The separation of

Hydrodynamic chromatography ofpolymers
121
differently sized species takes place in the interstitial volume between the parti-
cles, where due to a velocity profile with the lower velocities close to the parti-
cles, the larger species that are excluded from this region elute earlier than the
smaller species. Since the particles of the packing material generally are not uni-
form in size, the dimensions of the interstitial spaces between the particles is not
clearly defined.
Also,
the exact form of the velocity profile is not known. As a
result, estimation of the size of eluting species from relative residence times
alone, as can be done in microcapillary HDC, is hardly possible.
Ever since Small
[l-31
pioneered this technique in the early
1970s,
numerous
applications have been reported in the literature. Again, as in capillary HDC, the
majority of the articles deal with the separation of discrete particles. The popu-
larity of this technique stems, among other things, from the fact that under cer-
tain conditions, it is possible to construct a universal calibration curve.
Nagy
[37]
showed that latex particles with a different chemical composition, e.g.
polystyrene, vinyl acetate or vinyl chloride-ethylene, but also inorganic species
such as colloidal silica fall on the same curve of particle size versus relative
residence time. Thus, for particles of unknown composition, HDC in packed
columns makes it possible to calculate a reliable size. For a review of these
particle separations by packed column HDC, the reader is referred to McHugh
Again, applications
of
the separation of polymeric species are not numerous.
The majority are concerned with the characterization of xanthane polysaccharide
and polyacrylamide
of
high molecular mass, compounds that find use in en-
hanced oil recovery and as flocculants. Examples of the separation of these com-
pounds are given by Hoagland
et
al.
[7]
and Prud’homme
et
al.
[6].
Since no
calibration standards are available, their results are expressed as the “equivalent
particle diameter”.
A
problem with the separations mentioned above is the gen-
erally poor separation between the polymer elution profile and the peak of the
low molecular mass component that is used to determine the
t
=
1
point,
so
often
the “delayed marker injection technique”, described by McGowan and Langhorst
[38],
has to be used.
Langhorst and Stanley
[39]
used a low-angle light scattering detector to obtain
absolute molecular mass information on partially hydrolysed polyacrylamides.
Using
a
column filled with
15
pm ion-exchange particles, they found very broad
molecular mass distributions, extending up to a value of about
6
X
lo7
Da.
These are values that cannot easily be determined by size exclusion chromatog-
raphy due to the lack
of
efficient, small-particle packing materials with large
enough pores. Lecourtier and Chauveteau
[40]
used a capillary model to predict
polymer velocity in flow through porous media. They found good agreement
between predictions and HDC experiments on xanthane in columns packed with
irregular silicon carbide particles.
P11.
References pp.
125-126
