Абельсон Х., Сассман Д.Д. Структура и интерпретация компьютерных программ

Подождите немного. Документ загружается.

3.2. Моде ль вычислений с окружениями

231

• Процедура создается при вычислении lambda-выражения по отношению к некото-

рому окружению. Получающийся процедурный объект есть пара, состоящая из текста

lambda-выражения и указателя на окружение, в котором процедура была создана.

Кроме того, мы указываем, что когда символ определяется при помощи define,

в текущем кадре окружения создается связывание, и символу присваивается указан -

ное значение

. Наконец, мы описываем поведение set!, операции, из-за которой нам,

собственно, и пришлось ввести модель с окружениями. Вычисление выражения (set!

hпеременнаяi hзначениеi) в некотором окружении заставляет интерпр етатор найти

связывание переменной в окружении и изменить это связывание так, чтобы оно ука-

зывало на новое значение. А именно, нужно найти первый к адр окружения, в котором

содерж ится связывание для переменной, и изменить этот кадр. Если переменная в окру-

жении не связана, set! сигнализирует об ошибке.

Все эти правила вычисления, хотя они значительно сложнее, чем в подстановочной

модели, достаточно просты. Более того, модель вычислений, несмотря на свою абстракт-

ность, дает правильное описание того, как интерпретатор вычисляет выражения. В гла-

ве 4 мы увидим, как эта модель може т служить основой для реализации работающего

интерпретатора. В последующих разделах анализ нескольких примеров программ рас-

крывает некоторые детали этой модели.

3.2.2. Применение простых процедур

Когда в разделе 1.1.5 мы описывали подстановочную модель, мы показали, как вы-

числение комбинации (f 5) дает резул ьтат 136, если даны следующие определения:

(define (square x)

(* x x))

(define (sum-of-squares x y)

(+ (square x) (square y)))

(define (f a)

(sum-of-squares (+ a 1) (* a 2)))

Теперь мы можем проанализировать тот же самый пример, используя модель с окруже-

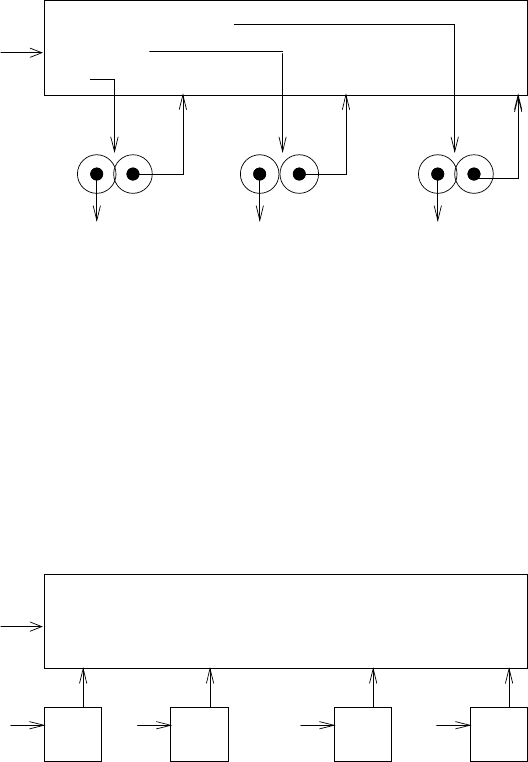
ниями. На рисунке 3.4 изображены три процедурных объекта, созданные вычислением

в глобальном окружении определений f, square, и sum-of-squares. Каждый проце-

дурный объект состоит из куска кода и указателя на глобальное окружение.

На рисунке 3.5 мы видим структуру окружений, созданную вычислением выражения

(f 5). Вызов f создает новое окружение E1, начинающееся с кадра, в котором a,

формальный параметр f, связывается с аргументом 5. В окружении E1 мы вычисляем

тело f:

(sum-of-squares (+ a 1) (* a 2))

Если в текущем кадре уже имелось связывание для указанной переменной, то это связывание изменяет-

ся. Это правило удобно, поскольку позволяет переопределять символы; однако оно означает, что при помощи

define можно изменять значение символов, а это влечет за собой все проблемы, связанные с присваиванием,

без явного использования set!. По этой причине некоторые предпочитают, чтобы переопределение существу-

ющего символа вызывало предупреждение или сообщение об ошибке.

232

Глава 3. Модульность, объекты и состояние

square:

sum-of-squares:

глобальное

окружение

параметры: a параметры: x параметры: x, y

тело: (sum-of-squares тело: (= x x) тело: (+ (square x)

(+ a 1) (square y))

(+ a 2))

Рис. 3.4. Процедурные объекты в глобальном кадре окружения.

глобальное

окружение

x:6a:5

y:10

x:6

x:10

E1 E2 E3 E4

(sum-of-squares (+ (square x) (* x x) (* x x)

(+ a 1) (square y))

(+ a 2))

Рис. 3.5. Окружения, созданные при вычислении (f 5) с использованием процедур,

изображенных на рис. 3.4

3.2. Моде ль вычислений с окружениями

233

Для вычисления этой комбинации сначала мы вычисляем подвыражения. Значение

первого подвыражения, sum-of-squares — процедурный объект. (Обрати те внимание,

как мы находим этот объект: снач ала мы просматриваем первый кадр E1, который не

содерж ит связывания для переменной sum-of-squares. Затем мы переходим в объем-

лющее окружение, а именно глобальное, и там находим связывание, которое показано на

рис. 3.4.) В оставшихся двух подвыражениях элементарные операции + и * применяются

при вычислении комбинаций (+ a 1) и (* a 2), и дают, соответственно, результаты

6 и 10.

Теперь мы применяем процедурный объект sum-of-squares к аргументам 6 и 10.

При этом создается новое окружение E2, в котором формальные параметры x и y связы-

ваются со значениями аргументов. Внутри E2 мы вычисляем комбинацию (+ (square

x) (square y)). Для этого нам требуется вычислить (square x), причем значение

square мы находим в глобальном окружении, а x равен 6. Мы опять создаем новое

окружение, E3, где x связан со значением 6, и где мы вычисляем тело square, то есть

(* x x). Кроме того, как часть вычисления sum-of-squares, нам нужно вычислить

подвыражение (square y), где y равен 10. Этот второй вызов square создает еще

одно окружение E4, в котором x, формальный параметр square, связан со значением

10. Внутри E4 нам нужно вычислить (* x x).

Важно заметить, что каждый вызов square создает новое окружение с новым связы-

ванием для x. Теперь мы видим, как разделение кадров служит для того, чтобы разные

локальные переменные по имени x не смешивались. Заметим, кроме того, что все кадры,

созданные процедурой square, указывают на глобальное окружение, поскольку указа-

тель именно на это окружение содержится в процедурном объекте square.

После того, как подвыражения вычисляются, они возвращают значения. Значения,

порожденные двумя вызовами square, складываются в sum-ofsquares, и этот ре-

зультат возвращается процедурой f. Поскольку сейчас наше внимание сосредоточено

на с труктурах окружений, мы не будем здесь разбираться, как значения передаются от

вызова к вызову; однако на самом деле это важная часть процесса вычисления, и мы

детально рассмотрим ее в главе 5.

Упражнение 3.9.

В разделе 1.2.1 мы с помощью подстановочной модели анализировали д ве процедуры вычисления

факториала, рекурсивную

(define (factorial n)

(if (= n 1)

(* n (factorial (- n 1)))))

и итеративную

(define (factorial n)

(fact-iter 1 1 n))

(define (fact-iter product counter max-count)

(if (> counter max-count)

product

(fact-iter (* counter product)

(+ counter 1)

max-count)))

234

Глава 3. Модульность, объекты и состояние

Продемонстрируйте, какие структуры окружений возникнут при вычислении (factorial 6) с

каждой из версий процедуры factorial

3.2.3. Кадры как хранилище внутреннего состояния

Теперь мы можем обратиться к модели с окружениями и рассмотре ть, как можно

с помощью процедур и присваивания представлять объекты, обладающие внутренним

состоя нием. В качестве примера возьмем «обработчик снятия денег со счета» из разде-

ла 3.1.1, который создается вызовом процедуры

(define (make-withdraw balance)

(lambda (amount)

(if (>= balance amount)

(begin (set! balance (- balance amount))

balance)

"Недостаточно денег на счете")))

Опишем вычисление

(define W1 (make-withdraw 100))

за которым следует

(W1 50)

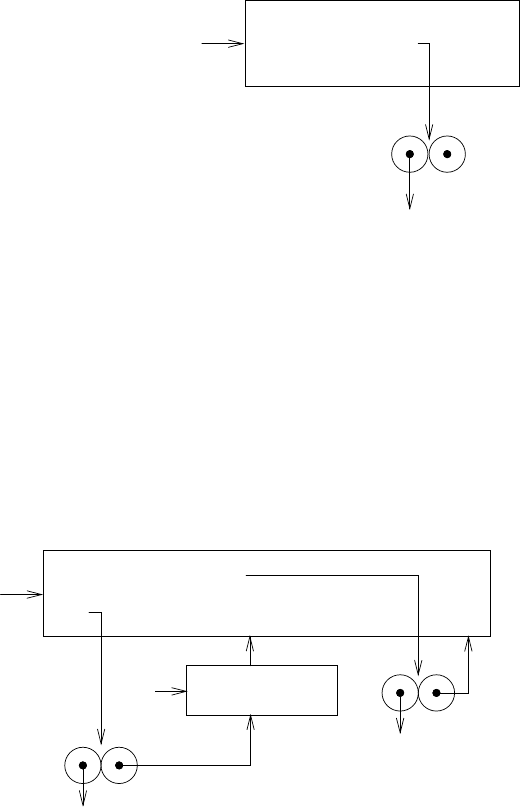
На рисунке 3.6 показан результат опреде ления make-withdraw в глобальном окруже-

нии. Получ ается процедурный объект, который содержит ссылку на глобал ьное окру-

жение. До сих пор мы не видим особых отличий от тех примеров, которые мы уже

рассмотрели, кроме того, что тело процедуры само по себе является ля мбда-выражением.

Интересная часть вычисления начинается тогда, когда мы применяем процедуру

make-withdraw к аргументу:

(define W1 (make-withdraw 100))

Сначала, как обычно, мы создаем окружение E1, где формальный параметр balance свя-

зан с аргументом 100. Внутри этого окружения мы вычисляем тело make-withdraw, а

именно lambda-выражение. При этом создае тся новый процедурный объект, код ко то-

рого определяется lambda-выражением, а окружение равно E1, окружению, в котор ом

вычисляется lambda при создании процедуры. Полученный процедурный объект возвра-

щается в качес тве значения процедуры make-withdraw. Это значение присваивается

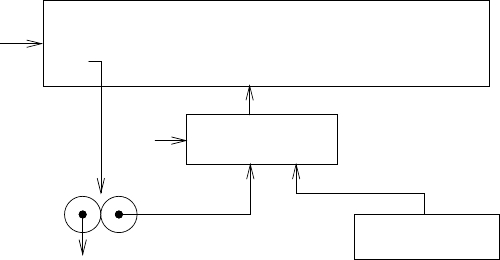
переменной W1 в глобальном окружении, поскольку выражение define вычисляется

именно в нем. Получившаяся структура окружений изображена на рисунке 3.7.

Теперь можно проанализировать, что происходит, когда W1 применяется к аргументу:

(W1 50)

Модель с окружени ями неспособна проилл юстрировать утверждение из раздела 1.2.1, что интерпретатор

может, используя хвостовую рекурсию, вычислять процедуры, подобные fact-iter, в фиксированном объеме

памяти. Мы рассмотрим хвостовую рекурсию, когда будем изучать управляющую структуру интерпретатора в

разделе 5.4.

3.2. Моде ль вычислений с окружениями

235

глобальное

окружение

make-withdraw:

параметры: balance

тело: (lambda (amount)

(if (>= balance amount)

(begin (set! balance (- balance amount))

balance)

"Недостаточно денег на счете"))

Рис. 3.6. Результат определения make-withdraw в глобальном окружении.

make-withdraw:...

W1:

balance: 100

balance

глобальное

параметры:

тело:...

окружение

параметры: amount

тело: (if (>= balance amount)

(begin (set! balance (-balance amount))

balance)

"Недостаточно денег на счете"))

Рис. 3.7. Результат вычисления (define W1 (make-withdraw 100)).

236

Глава 3. Модульность, объекты и состояние

make-withdraw:...

W1:

balance: 100

amount: 50

изменен операцией

set!.

Баланс, который будет

глобальное

окружение

параметры: amount (if (>= balance amount)

(begin

(set! (balance

(- balance amount))

balance

"Недостаточно денег на счете"))

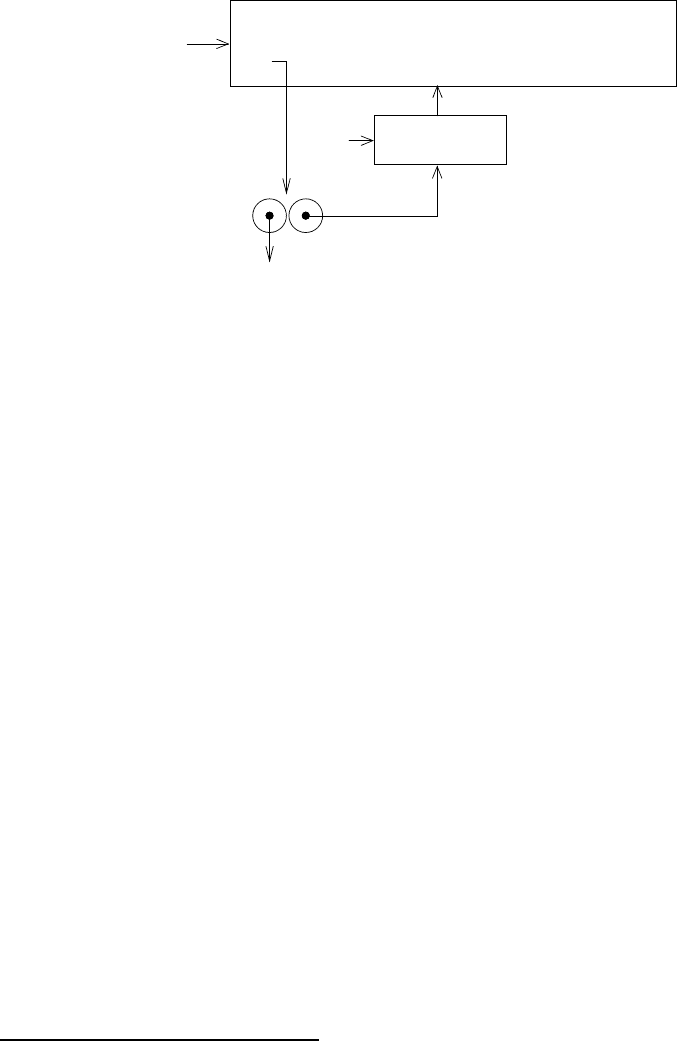
Рис. 3.8. Окружения, создаваемые при применении процедурного объекта W1.

Для начала мы конструируем кадр, в котором amount, формальный параметр W1, свя-

зывается со значением 50. Здесь крайне важно з аметить, что у этого кадра в качестве

объемлющего окружения выступает не глобальное окружение, а E1, поскольку именно

на него ук азывает процедурный объект W1. В этом новом окружении мы вычисляем тело

процедуры:

(if (>= balance amount)

(begin (set! balance (- balance amount))

balance)

"Недостаточно денег на счете")

Получается структура окружений, изображенная на рисунке 3.8. Вычисляемое выраже-

ние обращается к перемен ным amount и balance. Amount находится в первом кадре

окружения, а balance мы найдем, проследовав по указателю на объемлющее окруже-

ние E1.

Когда выполняется set!, связывание переменной balance в E1 изменяется. После

завершения вызова W1 значение balance равно 50, а W1 по-прежнему указывает на

кадр, который содержит переменную balance. Кадр, содержащий amount (тот, в кото-

ром мы выполняли код, изменяющий balance), больше не нужен, поскольку создавший

его вызов процедуры закончен, и никаких указателей на этот кадр из других частей

окружения нет. В следующий раз, когда мы позовем W1, создастся новый кадр, в кото-

ром будет связана переменная amount, и для которого объемлющим окружением снова

будет E1. Мы видим, что E1 служит «местом», в котором хранится локал ьная пере-

менная окружения для процедурного объекта W1. На рисунке 3.9 изображена ситуация

3.2. Моде ль вычислений с окружениями

237

make-withdraw:...

W1:

balance:50

глобальное

окружение

параметры: amount

тело: ...

Рис. 3.9. Окружен ия после вызова W1.

после вызова W1.

Рассмотрим, что произойде т, когда мы создадим другой объект для «снятия денег»,

вызвав make-withdraw второй раз:

(define W2 (make-withdraw 100))

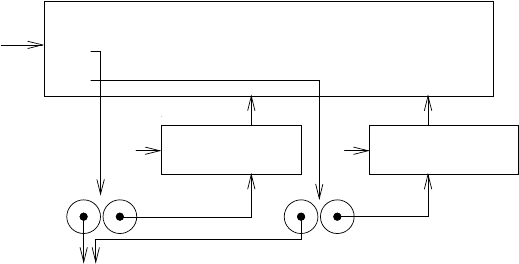
При этом получается структура окружений, изображенная на рисунке 3.10. Мы видим,

что W2 — процедурный объект, то есть пара, содержащая код и окружение. Окружение

E2 для W2 было создано во время вызова make-withdraw. Оно содержит кадр со своим

собственн ым связыванием переменной balance. С другой стороны, код у W1 и W2 один

и тот же: это код, определяемый lambda-выражением в теле make-withdraw

. Отсюда

мы видим, почему W1 и W2 ведут себя как независимые объекты. Вызовы W1 работают

с переменной состояния balance, которая хранится в E1, а вызовы W2 с переменной

balance, хранящейся в E2. Таким о бразом, изменения внутреннего состояния одного

объекта не действуют на другой.

Упражнение 3.10.

В процедуре make-withdraw локальная переменная balance создается в виде параметра make-

withdraw. Можно было бы создать локальную переменную и явно, используя let, а именно:

(define (make-withdraw initial-amount)

(let ((balance initial-amount))

(lambda (amount)

(if (>= balance amount)

(begin (set! balance (- balance amount))

balance)

"Недостаточно денег на счете"))))

Разделяют ли W1 и W2 общий физический код, хранимый в компьютере, или каждый из них хранит

собственную копию кода — это деталь реализации. В интерпретаторе, который мы создадим в главе 4, код

будет общим.

238

Глава 3. Модульность, объекты и состояние

make-withdraw:...

W2:

W1:

balance: 100balance: 50

E2E1

окружение

глобальное

параметры: amount

тело: ...

Рис. 3.10. Со здание второго объекта при помощи (define W2 (make-withdraw

100))

Напомним, что в разделе 1.3.2 говорится, что let всего лишь синтаксический сахар для вызова

процедуры:

(let ((hперi hвырi))

hтелоi)

интерпретируется как альтернативный синтаксис для

((lambda (hперi) hтелоi) hвырi)

С помощью модели с окружениями проанализируйте альтернативную версию makewithraw. На-

рисуйте картинки, подобные приведенным в этом разделе, для выражений

(define W1 (make-withdraw 100))

(W1 50)

(define W2 (make-withdraw 100))

Покажите, что две версии make-withdraw создают объекты с одинаковым поведением. Как раз-

личаются структуры окружений в двух версиях?

3.2.4. Внутренние определения

В разделе 1.1.8 мы познакомились с идеей, что процедуры могут содержать внут-

ренние определения, в результате чего возникает блочная структура, как, например, в

следующей процедуре вычисления квадратного корня:

(define (sqrt x)

(define (good-enough? guess)

(< (abs (- (square guess) x)) 0.001))

3.2. Моде ль вычислений с окружениями

239

глобальное

окружение

sqrt:

guess:1

x:2

good-enough?:

improve:...

sqrt-iter:...

параметры:

тело:

параметры:

тело:

(define improve ...)

(define sqrt-iter ...)

sqrt-iter

good-enough?

(sqrt-iter 1.0)

вызов

(define good-enough? ...)

(< (abs ...)

...)

guess

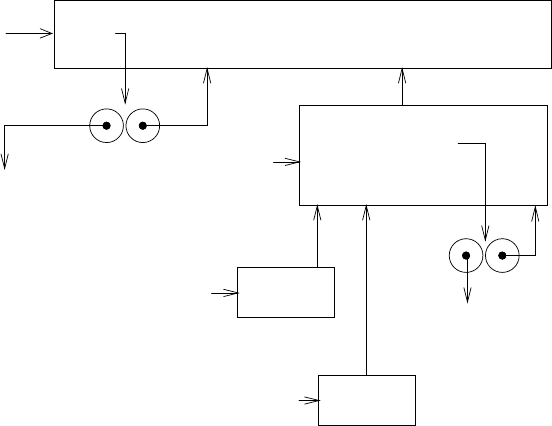
Рис. 3.11. Процедура sqrt с внутренними определениями.

(define (improve guess)

(average guess (/ x guess)))

(define (sqrt-iter guess)

(if (good-enough? guess)

guess

(sqrt-iter (improve guess))))

(sqrt-iter 1.0))

Теперь с помощью модели с окружениями мы можем увидеть, почему эти внутренние

определения работают так, как должны. На рисунке 3.11 изображен момент во время вы-

числения выражения (sqrt 2), когда внутренняя процедура good-enough? вызвана

в первый раз со значением guess, равн ым 1.

Рассмотрим структуру окружения. Символ sqrt в глобальном окружении связан с

процедурным объектом, ассоциированное окружение которого — глобальное окружение.

Когда мы вызвали процедуру sqrt, появилось окружение E1, зависимое от глобального,

в котором параметр x связан со значением 2. Затем мы вычислили тело sqrt внутри

E1. Поскольку первое выражение в теле sqrt есть

(define (good-enough? guess)

(< (abs (- (square guess) x)) 0.001))

вычисление этого выражения привело к определению процедуры good-enough? в окру-

жении E1. Выражаясь более точно, к первому кадру E1 был добавлен символ good-

enough?, связанный с процедурным объектом, ассоциированным окружением которо-

го является E1. Подобным образом в качестве процедур внутри E1 были определены

240

Глава 3. Модульность, объекты и состояние

improve и sqrt-iter. Краткости ради на рис. 3.11 показан только процедурный объ-

ект, соответствующий good-enough?.

После того, как были опреде лены внутренние процедуры, мы вычислили выражение

(sqrt-iter 1.0), по-прежнему в окружении E1. То есть, процедурный объект, свя-

занный в E1 с именем sqrt-iter, был вызван с аргументом 1. При э том появилось

окружение E2, в котором guess, параметр sqrt-iter, связан со значением 1. В свою

очередь, sqrt-iter вызвала good-enough? со значением guess (из E2) в качестве

аргумента. Получилось еще одно окружение, E3, в котором guess (параметр good-

enough?) связан со значением 1. Несмотря на то, что и sqrt-iter, и good-enough?

имеют по параметру с одинаковым именем guess, это две различные переменные, распо-

ложенные в разных кадрах. Кроме того, и E2, и E3 в качестве объемлющего окружения

имеют E1, поскольку как sqrt-iter, так и good-enough? в качестве окружения со-

держат указатель на E1. Одним из следствий этого является то, что символ x в теле

good-enough? обозначает связывание x, в окружении E1, а точнее, то значение x, с

которым была вызвана исходная процедура sqrt.

Так им образом, модель вычислений с окружениями объясняет две ключевых особен-

ности, которые делают внутренние определения процедур полезным способом модуляри-

зации программ:

• Имена внутрен них процедур не путаются с именами, внешними по отношению к

охватывающей процедуре, поскольку локальные имена процедур будут связываться в

кадре, который процедура создает при своем запуске, а не в глобальном окружении.

• Внутренние процедуры могут обращаться к аргументам охватывающих процедур,

просто используя имена параметров как свободные переменные. Это происходит потому,

что тело внутренней процедуры выполняется в окружении, подчиненном окружению, где

вычисляется объемлющая процедура.

Упражнение 3.11.

В разделе 3.2.3 мы видели, как модель с окружениями описы вает поведение процедур, облада-

ющих внутренним состоянием. Теперь м ы рассмотрели, как работают локальные определения.

Типичная процедура с передачей сообщений пользуется и тем, и другим. Рассмотрим процедуру

моделирования банковского счета из раздела 3.1.1:

(define (make-account balance)

(define (withdraw amount)

(if (>= balance amount)

(begin (set! balance (- balance amount))

balance)

"Недостаточно денег на счете"))

(define (deposit amount)

(set! balance (+ balance amount))

balance)

(define (dispatch m)

(cond ((eq? m ’withdraw) withdraw)

((eq? m ’deposit) deposit)

(else (error "Неизвестный вызов -- MAKE-ACCOUNT"

m))))

dispatch)