A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

Подождите немного. Документ загружается.

120 9 Joint distributions and independence

-0.4

-0.2

0.2

0.4

-0.4

-0.2

0.2

0.4

f(x,y)

Fig. 9.2. A bivariate normal probability density function.

density function

f(x, y)=



y + xy



for 0 ≤ x ≤ 3and1≤ y ≤ 2,

and f (x, y) = 0 otherwise; see Figure 9.3.

0,2

2,5

0,4

0,6

1,5

0,8

0,5

-1

1,2

Fig. 9.3. The probability density function f (x, y)=



y + xy



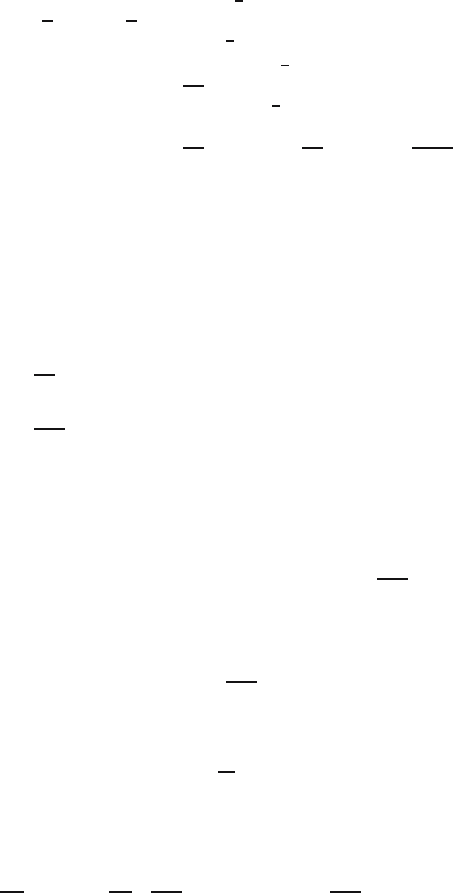
9.2 Joint distributions of continuous random variables 121

As an illustration of how to compute joint probabilities:



1 ≤ X ≤ 2,

≤ Y ≤





f(x, y)dx dy







(2x

y + xy

)dy









dx =

187

2025

Next, for a between0and3andb between 1 and 2, we determine the ex-

pression of the joint distribution function. Since f(x, y)=0forx<0or

y<1,

F (a, b)=P(X ≤ a, Y ≤ b)=



−∞





−∞

f(x, y)dy









(2x

y + xy

)dy



225



− 2a

+ a

− a



Note that for either a outside [0, 3] or b outside [1, 2], the expression for F (a, b)

is diﬀerent. For example, suppose that a isbetween0and3andb is larger

than 2. Since f (x, y)=0fory>2, we ﬁnd for any b ≥ 2:

F (a, b)=P(X ≤ a, Y ≤ b)=P(X ≤ a, Y ≤ 2) = F (a, 2) =

225



+7a



Hence, applying (9.1) one ﬁnds the marginal distribution function of X:

(a) = lim

b→∞

F (a, b)=

225



+7a



for a between 0 and 3.

Quick exercise 9.4 Show that F

(b)=



+18b

−21



for b between 1

and 2.

The probability density of X can be found by diﬀerentiating F

(x)=



225



+7x





225



+7x



for x between 0 and 3. It is also possible to obtain the probability density

function of X directly from f (x, y). Recall that we determined marginal prob-

abilities of discrete random variables by summing over the joint probabilities

(see Table 9.2). In a similar way we can ﬁnd f

.Forx between 0 and 3,

122 9 Joint distributions and independence

(x)=



∞

−∞

f(x, y)dy =





y + xy



dy =

225



+7x



This illustrates the following rule.

From joint to marginal probability density function. Let

f be the joint probability density function of random variables X

and Y . Then the marginal probability densities of X and Y can be

found as follows:

(x)=



∞

−∞

f(x, y)dy and f

(y)=



∞

−∞

f(x, y)dx.

Hence the probability density function of each of the random variables X and

Y can easily be obtained by “integrating out” the other variable.

Quick exercise 9.5 Determine f

(y).

9.3 More than two random variables

To determine the joint distribution of n random variables X

,...,X

,all

deﬁned on the same sample space Ω, we have to describe how the probability

mass is distributed over all possible values of (X

,...,X

). In fact, it

suﬃces to specify the joint distribution function F of X

,...,X

,which

is deﬁned by

F (a

,...,a

)=P(X

≤ a

,...,X

≤ a

)

for −∞ <a

,...,a

< ∞.

In case the random variables X

,...,X

are discrete, the joint distribution

can also be characterized by specifying the joint probability mass function p

of X

,...,X

, deﬁned by

p(a

,...,a

)=P(X

= a

,...,X

= a

)

for −∞ <a

,...,a

< ∞.

Drawing without replacement

Let us illustrate the use of the joint probability mass function with an example.

In the weekly Dutch National Lottery Show, 6 balls are drawn from a vase

that contains balls numbered from 1 to 41. Clearly, the ﬁrst number takes

values 1, 2,...,41 with equal probabilities. Is this also the case for—say—the

third ball?

9.3 More than two random variables 123

Let us consider a more general situation. Suppose a vase contains balls num-

bered 1, 2,...,N.Wedrawn balls without replacement from the vase. Note

that n cannot be larger than N. Each ball is selected with equal probability,

i.e., in the ﬁrst draw each ball has probability 1/N , in the second draw each of

the N −1 remaining balls has probability 1/(N −1), and so on. Let X

denote

the number on the ball in the i-th draw, for i =1, 2,...,n. In order to obtain

the marginal probability mass function of X

, we ﬁrst compute the joint proba-

bility mass function of X

,...,X

. Since there are N (N −1) ···(N −n+1)

possible combinations for the values of X

,...,X

,eachhavingthesame

probability, the joint probability mass function is given by

p(a

,...,a

)=P(X

= a

,...,X

= a

)

N(N − 1) ···(N − n +1)

for all distinct values a

,...,a

with 1 ≤ a

≤ N . Clearly X

,...,X

inﬂuence each other. Nevertheless, the marginal distribution of each X

the same. This can be seen as follows. Similar to obtaining the marginal

probability mass functions in Table 9.2, we can ﬁnd the marginal probability

mass function of X

by summing the joint probability mass function over all

possible values of X

,...,X

i−1

i+1

,...,X

(k)=



p(a

,...,a

i−1

,k,a

i+1

,...,a

)



N(N − 1) ···(N − n +1)

where the sum runs over all distinct values a

,...,a

with 1 ≤ a

≤ N

and a

= k. Since there are (N −1)(N −2) ···(N −n + 1) such combinations,

we conclude that the marginal probability mass function of X

is given by

(k)=(N − 1)(N −2) ···(N − n +1)·

N(N − 1) ···(N − n +1)

for k =1, 2,...,N. We see that the marginal probability mass function of

each X

is the same, assigning equal probability 1/N to each possible value.

In case the random variables X

,...,X

are continuous, the joint dis-

tribution is deﬁned in a similar way as in the case of two variables. We say

that the random variables X

,...,X

have a joint continuous distribu-

tion if for some function f : R

→ R and for all numbers a

,...,a

and

,...,b

with a

≤ b

P(a

≤ X

≤ b

≤ X

≤ b

,...,a

≤ X

≤ b

)



···



f(x

,...,x

)dx

··· dx

Again f has to satisfy f(x

,...,x

) ≥ 0andf has to integrate to 1. We

call f the joint probability density of X

,...,X

124 9 Joint distributions and independence

9.4 Independent random variables

In earlier chapters we have spoken of independence of random variables, an-

ticipating a formal deﬁnition. On page 46 we postulated that the events

= a

}, {R

= a

},...,{R

= a

}

related to the Bernoulli random variables R

,...,R

are independent. How

should one deﬁne independence of random variables? Intuitively, random vari-

ables X and Y are independent if every event involving only X is indepen-

dent of every event involving only Y . Since for two discrete random variables

X and Y , any event involving X and Y is the union of events of the type

{X = a, Y = b}, an adequate deﬁnition for independence would be

P(X = a, Y = b)=P(X = a)P(Y = b) , (9.3)

for all possible values a and b. However, this deﬁnition is useless for continuous

random variables. Both the discrete and the continuous case are covered by

the following deﬁnition.

Definition. The random variables X and Y , with joint distribution

function F ,areindependent if

P(X ≤ a, Y ≤ b)=P(X ≤ a)P(Y ≤ b) ,

that is,

F (a, b)=F

(a)F

(b) (9.4)

for all possible values a and b. Random variables that are not inde-

pendent are called dependent.

Note that independence of X and Y guarantees that the joint probability of

{X ≤ a, Y ≤ b} factorizes. More generally, the following is true: if X and Y

are independent, then

P(X ∈ A, Y ∈ B)=P(X ∈ A)P(Y ∈ B) , (9.5)

for all suitable A and B, such as intervals and points. As a special case we

can take A = {a}, B = {b}, which yields that for independent X and Y the

probability of {X = a, Y = b} equals the product of the marginal probabilities.

In fact, for discrete random variables the deﬁnition of independence can be

reduced—after cumbersome computations—to equality (9.3). For continuous

random variables X and Y we ﬁnd, diﬀerentiating both sides of (9.4) with

respect to x and y,that

f(x, y)=f

(x)f

(y).

9.5 Propagation of independence 125

Quick exercise 9.6 Determine for which value of ε the discrete random

variables X and Y from Quick exercise 9.2 are independent.

More generally, random variables X

,...,X

, with joint distribution func-

tion F ,areindependent if for all values a

,...,a

F (a

,...,a

)=F

) ···F

As in the case of two discrete random variables, the discrete random variables

,...,X

are independent if

P(X

= a

,...,X

= a

)=P(X

= a

) ···P(X

= a

) ,

for all possible values a

,...,a

. Thus we see that the deﬁnition of inde-

pendence for discrete random variables is in agreement with our intuitive

interpretation given earlier in (9.3).

In case of independent continuous random variables X

,...,X

with joint

probability density function f , diﬀerentiating the joint distribution function

with respect to all the variables gives that

f(x

,...,x

)=f

) ···f

) (9.6)

for all values x

,...,x

. By integrating both sides over (−∞,a

]×(−∞,a

]×

···×(−∞,a

], we ﬁnd the deﬁnition of independence. Hence in the continuous

case, (9.6) is equivalent to the deﬁnition of independence.

9.5 Propagation of independence

A natural question is whether transformed independent random variables are

again independent. We start with a simple example. Let X and Y be two

independent random variables with joint distribution function F .Takean

interval I =(a, b] and deﬁne random variables U and V as follows:

U =



1ifX ∈ I

0ifX/∈ I,

and V =



1ifY ∈ I

0ifY/∈ I.

Are U and V independent? Yes, they are! By using (9.5) and the independence

of X and Y ,wecanwrite

P(U =0,V =1)=P(X ∈ I

,Y ∈ I)

=P(X ∈ I

)P(Y ∈ I)

=P(U =0)P(V =1).

By a similar reasoning one ﬁnds that for all values a and b,

126 9 Joint distributions and independence

P(U = a, V = b)=P(U = a)P(V = b) .

This illustrates the fact that for independent random variables X

,...,X

the random variables Y

,...,Y

,whereeachY

is determined by X

only,

inherit the independence from the X

. The general rule is given here.

Propagation of independence. Let X

,...,X

be indepen-

dent random variables. For each i,leth

: R → R be a function and

deﬁne the random variable

= h

Then Y

,...,Y

are also independent.

Often one uses this rule with all functions the same: h

= h. For instance, in

the preceding example,

h(x)=



1ifx ∈ I

0ifx/∈ I.

The rule is also useful when we need diﬀerent transformations for diﬀerent

. We already saw an example of this in Chapter 6. In the single-server

queue example in Section 6.4, the Exp(0.5) random variables T

,... and

U(2, 5) random variables S

,... are required to be independent. They are

generated according to the technique described in Section 6.2. With a se-

quence U

,...of independent U (0, 1) random variables we can accomplish

independence of the T

and S

as follows:

= F

inv

2i−1

)andS

= G

inv

where F and G are the distribution functions of the Exp (0.5) distribution and

the U (2, 5) distribution. The propagation-of-independence rule now guaran-

tees that all random variables T

,... are independent.

9.6 Solutions to the quick exercises

9.1 The only possibilities with the sum equal to 7 and the maximum equal

to 4 are the combinations (3, 4) and (4, 3). They both have probability 1/36,

so that P(S =7,M =4)=2/36.

9.2 Since p

(0), p

(1), p

(0), and p

(1) are all equal to 1/2, knowing only

and p

yields no information on ε whatsoever. You have to be a student

at Hogwarts to be able to get the values of p right!

9.3 Since S and M are discrete random variables, F (5, 3) is the sum of the

probabilities P(S = a, M = b) of all combinations (a, b)witha ≤ 5andb ≤ 3.

From Table 9.2 we see that this sum is 8/36.

9.7 Exercises 127

9.4 For a between0and3andforb between 1 and 2, we have seen that

F (a, b)=

225



− 2a

+ a

− a



Since f(x, y)=0forx>3, we ﬁnd for any a ≥ 3andb between 1 and 2:

F (a, b)=P(X ≤ a, Y ≤ b)=P(X ≤ 3,Y ≤ b)

= F (3,b)=



+18b

− 21



As a result, applying (9.2) yields that F

(b) = lim

a→∞

F (a, b)=F (3,b)=



+18b

− 21



,forb between 1 and 2.

9.5 For y between 1 and 2, we have seen that F

(y)=



+18y

− 21



Diﬀerentiating with respect to y yields that

(y)=

(3y

+12y),

for y between1and2(andf

(y) = 0 otherwise). The probability density

function of Y can also be obtained directly from f(x, y). For y between 1

and 2:

(y)=



∞

−∞

f(x, y)dx =



(2x

y + xy

)dx



y +



x=3

x=0

(3y

+12y).

Since f (x, y) = 0 for values of y not between 1 and 2, we have that f

(y)=



∞

−∞

f(x, y)dx =0forthesey’s.

9.6 The number ε is between −1/4and1/4. Now X and Y are independent

in case p(i, j)=P(X = i, Y = j)=P(X = i)P(Y = j)=p

(i)p

(j), for all

i, j =0, 1. If i = j = 0, we should have

− ε = p(0, 0) = p

(0) p

(0) =

This implies that ε =0.Furthermore,forallothercombinations(i, j)one

can check that for ε =0alsop(i, j)=p

(i) p

(j), so that X and Y are

independent. If ε =0,wehavep(0, 0) = p

(0) p

(0), so that X and Y are

dependent.

9.7 Exercises

9.1 The joint probabilities P(X = a, Y = b) of discrete random variables X

and Y are given in the following table (which is based on the magical square

in Albrecht D¨urer’s engraving Melencolia I in Figure 9.4). Determine the

marginal probability distributions of X and Y , i.e., determine the probabilities

P(X = a)andP(Y = b)fora, b =1, 2, 3, 4.

128 9 Joint distributions and independence

Fig. 9.4. Albrecht D¨urer’s Melencolia I.

Albrecht D¨urer (German, 1471-1528) Melencolia I, 1514. Engraving. Bequest

of William P. Chapman, Jr., Class of 1895. Courtesy of the Herbert F. Johnson

Museum of Art, Cornell University.

b 1234

1 16/136 3/136 2/136 13/136

2 5/136 10/136 11/136 8/136

3 9/136 6/136 7/136 12/136

4 4/136 15/136 14/136 1/136

9.7 Exercises 129

9.2  The joint probability distribution of two discrete random variables X

and Y is partly given in the following table.

b 012 P(Y = b)

−1 ... ... ... 1/2

1 ... 1/2 ... 1/2

P(X = a) 1/6 2/3 1/6 1

a. Complete the table.

b. Are X and Y dependent or independent?

9.3 Let X and Y be two random variables, with joint distribution the Melen-

colia distribution, given by the table in Exercise 9.1. What is

a. P(X = Y )?

b. P(X + Y =5)?

c. P(1 <X≤ 3, 1 <Y ≤ 3)?

d. P((X, Y ) ∈{1, 4}×{1, 4})?

9.4 This exercise will be easy for those familiar with Japanese puzzles called

nonograms. The marginal probability distributions of the discrete random

variables X and Y are given in the following table:

b 12345P(Y = b)

1 5/14

2 4/14

3 2/14

4 2/14

5 1/14

P(X = a) 1/14 5/14 4/14 2/14 2/14 1

Moreover, for a and b from 1 to 5 the joint probability P(X = a, Y = b)is

either 0 or 1/14. Determine the joint probability distribution of X and Y .

9.5  Let η be an unknown real number, and let the joint probabilities

P(X = a, Y = b) of the discrete random variables X and Y be given by the

following table:

A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.