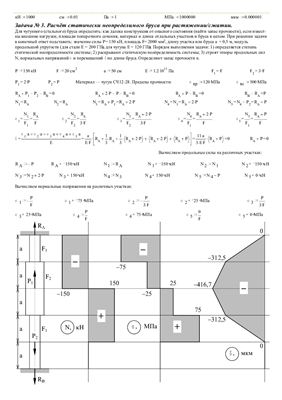
Задача № 3: Расчёт статически неопределимого бруса при
растяжении/сжатии.
Для чугунного (стального) бруса определить: как далека конструкция от опасного состояния (найти запас прочности), если известны внешние нагрузки, площади поперечного сечения, материал и длина отдельных участков и бруса в целом. При решении задачи в конечный ответ подставить: значение силы P = 150 кН, площадь F = 2000 мм2, длину участка или бруса a = 0,5 м, модуль продольной упругости (для стали E = 200 ГПа, для чугуна E = 120 ГПа). Порядок выполнения задачи: 1) определяется степень статической неопределимости системы; 2) раскрывают статическую неопределимость системы; 3) строят эпюры продольных сил N, нормальных напряжений σ и перемещений δ по длине бруса. Определяют запас прочности n.
Задача № 5: Расчёт статически неопределимого бруса при кручении.
Стальной брус защемлён по концам, нагружен двумя крутящими моментами, имеет поперечные сечения: круглое, круглое кольцевое, прямоугольное или тонкостенное замкнутое. Требуется: подобрать размеры (то есть размер a) поперечного сечения бруса, принимая значение момента M = 5000 Нм. Принять: величину допускаемого касательного напряжения [τ] = 80 МПа.
Порядок выполнения задачи: 1) Определить степень статической неопределённости. 2) Раскрыть статическую неопределённость, выразив крутящие моменты в сечениях через M; построить эпюру крутящих моментов. 3) Выразить в общем виде максимальные касательные напряжения на участках бруса (для участков прямоугольного поперечного сечения значения коэффициентов α в зависимости от h/b выбрать из таблицы 4.5). 4) Из условия прочности определить необходимый размер сечения a. 5) Построить эпюру углов закручивания. При решении уравнения углов поворота для брусьев, имеющих участки прямоугольного поперечного сечения значения коэффициентов β в зависимости от h/b выбрать из таблицы 4.5 Контрольная работа № 2; Задача № 6: Расчёт балок на изгиб.
Для заданной стальной балки с поперечным сечением в виде двутаврого профиля или двух швеллеров:
1). Из условия прочности по нормальным напряжениям изгиба подобрать величину допускаемой внешней нагрузки [q].
2). При найденной нагрузке подобрать сечение в виде прямоугольника с соотношением сторон h = 2b и сравнить расход материала с балкой двутаврового (швеллерового) профиля.
3). Определить угол поворота сечения на границе первого и второго (считая слева) участков. Определить прогиб балки в сечении, где приложена внешняя сила P. Каждое из перемещений балки определить двумя способами: а) используя дифференциальное уравнение упругой линии (или методом начальных параметров); б) энергетическим методом (способ Верещагина), сравнить результаты, полученные обоими способами.
4). Построить эпюры нормального напряжения в опасном сечении балки (для обоих вариантов сечений), имея в виду, что силовая линия совпадает с вертикальной осью сечения.
5). Построить эпюры касательного напряжения в поперечном сечении балки (для обоих вариантов сечений), каждый раз определяя их максимальные значения.
6). Показать примерное положение упругой линии балки с учётом найденных значений прогиба и угла поворота сечений; особенностей опорных устройств балки; эпюры изгибающего момента.
7). Принять для всех балок следующее соотношение: M = Pa = qa2, коэффициент запаса прочности n = 1,5.
Задача № 7: Расчёт на изгиб плоских статически определимых рам.
Для заданной плоской рамы
1). Построить эпюры поперечных и продольных сил и изгибающих моментов в поперечных сечениях рамы. Произвести проверку правильности построения эпюр внутренних силовых факторов способом вырезания узлов рамы.
2). Из условия прочности по нормальным напряжениям изгиба подобрать размеры поперечного сечения в виде прямоугольной трубы из двух швеллеров или двутавров.
3). Выполнить уточнённую проверку прочности по нормальным напряжениям с учётом продольных сил. Определить величину максимальных касательных напряжений.
4). Рассчитать перемещение рамы по направлению внешней силы P1, и угол поворота одного из узлов рамы энергетическим методом.
Принять следующее соотношение: M = Pa = qa2, а величину q = 10 кН. В случае, если не удастся подобрать сечения из приведённых в сортаменте, то, выбрав самое мощное сечение в сортаменте, определить для него расчётные напряжения и фактический запас прочности по нормальным напряжениям nф = σт/σmax.
Задача № 8: Расчёт сжатых стержней на устойчивость.
Для заданного сжатого стержня требуется: 1) Подобрать прокатный профиль сечения из условия обеспечения общей устойчивости стержня. Форму сечения выбрать согласно своему варианту по рис. 5.17. 2) Определить расстояние a между профилями в сечении из условия одинаковой устойчивости стержня в двух главных центральных плоскостях инерции. 3) Определить максимальное расстояние b между соединительными планками по длине стержня из условия обеспечения устойчивости части ветви стержня между планками. Определить необходимое количество соединительных планок и шаг их расстановки, (считая, что по концам стержня конструктивно имеются две пары соединительных планок). 4) Определить действительный коэффициент запаса устойчивости стержня в целом. 5) Определить гибкость и действительный коэффициент запаса устойчивости стержня в целом, с учётом податливости соединительных планок. При решении задачи модуль продольной упругости стали принять E = 200 ГПа.
Для всех эпюр определены формулы (функции) для единой переменной (расстояние от левого конца), и по этим функциям построены графики эпюр по тысячам точек, в том числе эпюры углов поворота сечений и прогибов нейтральной оси.
Автор Бечин А. В. Методичка: Лобанов Н. В. , IV семестр, специальность
140200. Постраничные рисунки в векторном формате EMF (в точности с тем, что рисует интерфейс Маткада). Масштаб можно увеличивать до предела или распечатывать; рисунки не будут из "квадратиков". В оригинале 2 Маткад-файла размером 111+267=378 кБ. А этот файл имеет размер всего 130 кБ, что почти в 3 раза меньше Маткад-оригинала. И это при том, что Маткад не сохраняет в файле результаты вычислений.
Для чугунного (стального) бруса определить: как далека конструкция от опасного состояния (найти запас прочности), если известны внешние нагрузки, площади поперечного сечения, материал и длина отдельных участков и бруса в целом. При решении задачи в конечный ответ подставить: значение силы P = 150 кН, площадь F = 2000 мм2, длину участка или бруса a = 0,5 м, модуль продольной упругости (для стали E = 200 ГПа, для чугуна E = 120 ГПа). Порядок выполнения задачи: 1) определяется степень статической неопределимости системы; 2) раскрывают статическую неопределимость системы; 3) строят эпюры продольных сил N, нормальных напряжений σ и перемещений δ по длине бруса. Определяют запас прочности n.
Задача № 5: Расчёт статически неопределимого бруса при кручении.
Стальной брус защемлён по концам, нагружен двумя крутящими моментами, имеет поперечные сечения: круглое, круглое кольцевое, прямоугольное или тонкостенное замкнутое. Требуется: подобрать размеры (то есть размер a) поперечного сечения бруса, принимая значение момента M = 5000 Нм. Принять: величину допускаемого касательного напряжения [τ] = 80 МПа.
Порядок выполнения задачи: 1) Определить степень статической неопределённости. 2) Раскрыть статическую неопределённость, выразив крутящие моменты в сечениях через M; построить эпюру крутящих моментов. 3) Выразить в общем виде максимальные касательные напряжения на участках бруса (для участков прямоугольного поперечного сечения значения коэффициентов α в зависимости от h/b выбрать из таблицы 4.5). 4) Из условия прочности определить необходимый размер сечения a. 5) Построить эпюру углов закручивания. При решении уравнения углов поворота для брусьев, имеющих участки прямоугольного поперечного сечения значения коэффициентов β в зависимости от h/b выбрать из таблицы 4.5 Контрольная работа № 2; Задача № 6: Расчёт балок на изгиб.
Для заданной стальной балки с поперечным сечением в виде двутаврого профиля или двух швеллеров:
1). Из условия прочности по нормальным напряжениям изгиба подобрать величину допускаемой внешней нагрузки [q].
2). При найденной нагрузке подобрать сечение в виде прямоугольника с соотношением сторон h = 2b и сравнить расход материала с балкой двутаврового (швеллерового) профиля.
3). Определить угол поворота сечения на границе первого и второго (считая слева) участков. Определить прогиб балки в сечении, где приложена внешняя сила P. Каждое из перемещений балки определить двумя способами: а) используя дифференциальное уравнение упругой линии (или методом начальных параметров); б) энергетическим методом (способ Верещагина), сравнить результаты, полученные обоими способами.
4). Построить эпюры нормального напряжения в опасном сечении балки (для обоих вариантов сечений), имея в виду, что силовая линия совпадает с вертикальной осью сечения.
5). Построить эпюры касательного напряжения в поперечном сечении балки (для обоих вариантов сечений), каждый раз определяя их максимальные значения.
6). Показать примерное положение упругой линии балки с учётом найденных значений прогиба и угла поворота сечений; особенностей опорных устройств балки; эпюры изгибающего момента.
7). Принять для всех балок следующее соотношение: M = Pa = qa2, коэффициент запаса прочности n = 1,5.
Задача № 7: Расчёт на изгиб плоских статически определимых рам.
Для заданной плоской рамы
1). Построить эпюры поперечных и продольных сил и изгибающих моментов в поперечных сечениях рамы. Произвести проверку правильности построения эпюр внутренних силовых факторов способом вырезания узлов рамы.
2). Из условия прочности по нормальным напряжениям изгиба подобрать размеры поперечного сечения в виде прямоугольной трубы из двух швеллеров или двутавров.
3). Выполнить уточнённую проверку прочности по нормальным напряжениям с учётом продольных сил. Определить величину максимальных касательных напряжений.
4). Рассчитать перемещение рамы по направлению внешней силы P1, и угол поворота одного из узлов рамы энергетическим методом.
Принять следующее соотношение: M = Pa = qa2, а величину q = 10 кН. В случае, если не удастся подобрать сечения из приведённых в сортаменте, то, выбрав самое мощное сечение в сортаменте, определить для него расчётные напряжения и фактический запас прочности по нормальным напряжениям nф = σт/σmax.
Задача № 8: Расчёт сжатых стержней на устойчивость.
Для заданного сжатого стержня требуется: 1) Подобрать прокатный профиль сечения из условия обеспечения общей устойчивости стержня. Форму сечения выбрать согласно своему варианту по рис. 5.17. 2) Определить расстояние a между профилями в сечении из условия одинаковой устойчивости стержня в двух главных центральных плоскостях инерции. 3) Определить максимальное расстояние b между соединительными планками по длине стержня из условия обеспечения устойчивости части ветви стержня между планками. Определить необходимое количество соединительных планок и шаг их расстановки, (считая, что по концам стержня конструктивно имеются две пары соединительных планок). 4) Определить действительный коэффициент запаса устойчивости стержня в целом. 5) Определить гибкость и действительный коэффициент запаса устойчивости стержня в целом, с учётом податливости соединительных планок. При решении задачи модуль продольной упругости стали принять E = 200 ГПа.
Для всех эпюр определены формулы (функции) для единой переменной (расстояние от левого конца), и по этим функциям построены графики эпюр по тысячам точек, в том числе эпюры углов поворота сечений и прогибов нейтральной оси.
Автор Бечин А. В. Методичка: Лобанов Н. В. , IV семестр, специальность
140200. Постраничные рисунки в векторном формате EMF (в точности с тем, что рисует интерфейс Маткада). Масштаб можно увеличивать до предела или распечатывать; рисунки не будут из "квадратиков". В оригинале 2 Маткад-файла размером 111+267=378 кБ. А этот файл имеет размер всего 130 кБ, что почти в 3 раза меньше Маткад-оригинала. И это при том, что Маткад не сохраняет в файле результаты вычислений.