СПбГАСУ, ПГС, 2 курс, 3 семестр. вариант 6: фотографии с печатным
текстом.
Тема - Определенные интегралы.
Вычислить площадь фигуры, ограниченной линиями. а) x^2=2-y x^2=y.
б) ρ=1-cosφ.
Найти длину дуги линии 9y^2=4(3+x)^3 от точки А(-3;0) до точки В(-1;(4√2)/3).
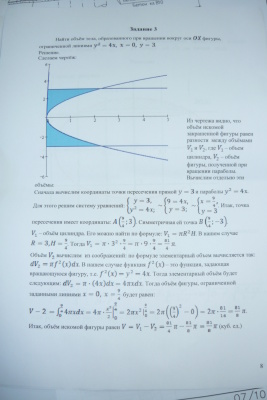
Найти объем тела, образованного при вращении вокруг оси ОХ фигуры, ограниченной линиями y^2=4x, x=0, y=3.
Найти площадь поверхности, образованной вращением вокруг тоси OY дуги кривой x= √2-y^2 от точки А(0, √2) до точки В(1,1).
Вычислить несобственные интегралы (или доказать их расходимость: а) ∫ dx/(√x^2-3) на луче от 2 до +∞. б) ∫((3x^2+2) /(√x+1))dx на отрезке от -1 до 0.
Тема - Определенные интегралы.
Вычислить площадь фигуры, ограниченной линиями. а) x^2=2-y x^2=y.
б) ρ=1-cosφ.
Найти длину дуги линии 9y^2=4(3+x)^3 от точки А(-3;0) до точки В(-1;(4√2)/3).
Найти объем тела, образованного при вращении вокруг оси ОХ фигуры, ограниченной линиями y^2=4x, x=0, y=3.
Найти площадь поверхности, образованной вращением вокруг тоси OY дуги кривой x= √2-y^2 от точки А(0, √2) до точки В(1,1).
Вычислить несобственные интегралы (или доказать их расходимость: а) ∫ dx/(√x^2-3) на луче от 2 до +∞. б) ∫((3x^2+2) /(√x+1))dx на отрезке от -1 до 0.